верно ли что в тупоугольном треугольнике все углы тупые
В тупом треугольнике все углы тупые
Здравствуйте!
Нужно ответить на два вопроса, вернее определить правильные ли утверждения:
Утверждение 1.
В тупо-м треугольнике все углы тупые.
Ответ 1.
Утверждение неверное.
Разберемся с понятием тупоугольного треугольника.
Раз он так называется, значит, тупой угол у него все же есть.
Может ли быть 2 тупых угла у такого треугольника? Как известно, градусная мера тупого угла больше 90 градусов. Если предположить, что у тупоугольного треугольника 2 тупых угла, то обозначим первый из них как (90 + а) градусов, а второй как (90 + b) градусов, где а и b – положительные значения.
Найдем сумму этих двух углов:
(90 + а) + (90 + b) = 180 + а + b
Мы нашли сумму ДВУХ предположительно тупых углов треугольника, которая уже больше 180 градусов. А согласно теореме о сумме ВСЕХ углов треугольника, она составляет 180 градусов. Следовательно, у тупоугольного треугольника даже двух тупых углов быть не может, а уж тем более всех.
Утверждение 2.
Диагонали в любом прямоугольнике разделяют его на 4 равные треугольника.
Ответ 2.
Утверждение неверно.
Рассмотрим диагонали произвольного прямоугольника. Известно, что они равны между собой, а также при пересечении точкой пересечения делятся на две равные части. 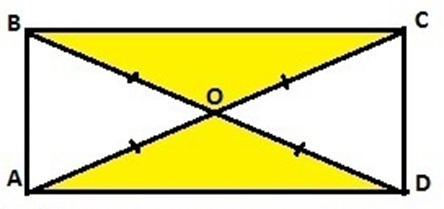
Тогда отрезки АО, ВО, СО и DO будут равными.
Также противоположные стороны у каждого прямоугольника равны. Значит отрезки АВ = CD и ВС = AD.
Рассмотрим треугольники АВО и CDO. Эти треугольники равны между собой по трем сторонам. Так же и треугольники ВСО и ADO будут равными по трем сторонам. Но в рассмотренных треугольниках не равны основания, то есть АВ не равно ВС и AD не равно ВС.
Поэтому треугольники АВО и ВСО не являются равными.
Таким же образом можно доказать неравенство и остальных треугольников, но этого достаточно, чтобы опровергнуть исходное утверждение.
В тупоугольном треугольнике все углы тупые
Здравствуйте!
Докажите правильность или неправильность утверждения:
В тупоугольном треугольнике все углы тупые.
Спасибо!
Утверждение.
В тупоугольном треугольнике все углы тупые.
Ответ.
Утверждение не верное.
Разберемся почему.
Для начала вспомним какой треугольник называется тупоугольным.
Тупоугольным называют треугольник, у которого один из углов тупой, то есть его градусная мера больше (а не равна) 90 градусов.
Теперь рассмотрим вопрос о том, могут ли все 3 угла треугольника быть тупыми, то есть большими 90 градусов.
Вспомним теорему о сумме углов любого из треугольников, которая равняется 180 градусов.
Теперь представим себе, что каждый угол треугольника больше 90 градусов. Обозначим такие углы как (90 + х) градусов, (90 + у) градусов и (90 + z) градусов. Найдем сумму этих трех углов:
(90 + х) + (90 + у) + (90 + z) = 180 (по теореме)
Раскроем скобки и упростим выражение:
270 + х + у + z = 180
Получили некорректное равенство, так как левая его часть никак не может быть равна правой при положительных значениях переменных х, у и z.
Таким образом, можно сделать вывод, что в тупоугольном треугольнике не может быть трех тупых углов.
Можно также доказать, что и двух тупых углов в треугольнике быть не может. Это делается так же, как и выполнялось доказательство заданного утверждения. То есть по сути тупоугольным называют треугольник, у которого всего лишь ОДИН тупой угол.
Верно ли что в тупоугольном треугольнике все углы тупые
RE: 1. Укажите номера верных утверждений. 1) В тупоугольном треугольнике все углы тупые. 2) В любо…
1. Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
2. Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
3. Какие из следующих утверждений верны?
1) Касательная к окружности параллельна радиусу, проведённому в точку касания.
2) Если в ромбе один из углов равен 90 градусам, то такой ромб — квадрат.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
4. Какое из следующих утверждений верно?
1) Диагонали ромба равны.
2) Отношение площадей подобных треугольников равно коэффициенту подобия.
3) Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.
5. Какие из следующих утверждений верны?
1) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
2) Все квадраты имеют равные площади.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны
Какие из утверждений верны В тупоугольном треугольнике все углы тупые Вертикальные углы равны Через точку, не лежащую на данной
Ответ:
Объяснение:
верны-Вертикальные углы равны.
Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
Ответ:
Площадь квадрата = 4*4=16
площади 4-х зеленых треугольников = 6 (4*3*1/2)
площади 2-х квадратов = 2
Площадь фигуры =16-6-2=8
Обозначим стороны треугольника Ав=4, ВС=5,АС=7. Проведём высоту СК из точки С на сторону АВ. Из точки К построим перпендикуляр-H (высота призмы).Найдём площадь основания по формуле Герона S=корень из 8(8-4)(8-5)(8-7)=4на корень из 6. Площадь основания также равна (АВ на КС):2. То есть (4 на КС):2=4 на корень из 6. Отсюда КС=2на корень из 6. По условию КМ=КС. Тогда V=S H=4корень из6умноженное на 2 корень из6=48.
Вторая задача.Призма правильная значит грань в котору ю вписана окружность-квадрат, а основание-равносторонний треугольник. АА=2. V=S H. H=2. Площадь основания по той же формуле корень из 1,5 0.5 0,5 0,5=корень из 3 делённое на 4. Тогда V=(корень из 3 ):4 умноженное на 2= (корень из3):2.
Тупоугольный треугольник, элементы, свойства, признаки и формулы
Тупоугольный треугольник, элементы, свойства, признаки и формулы.
Тупоугольный треугольник – это треугольник, у которого один угол тупой.
Тупоугольный треугольник (понятие и определение):
Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.
Рис. 1. Тупоугольный треугольник
∠ BАC– тупой угол треугольника,
Рис. 2. Равносторонний треугольник
АВ = ВС = АС – стороны треугольника,
Рис. 3. Прямоугольный треугольник
Рис. 4. Равнобедренный треугольник
АВ = AС – боковые стороны, BС – основание,
Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.
Элементы тупоугольного треугольника:
Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.
Рис. 5. Тупоугольный треугольник и внешний угол
Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.
Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника
MA – медиана тупоугольного треугольника
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника
MС – высота тупоугольного треугольника
Высота тупоугольного треугольника может лежать за пределами треугольника.
Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.
Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника
MA – биссектриса тупого угла тупоугольного треугольника
Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Свойства тупоугольного треугольника:
Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:
1. Против большей стороны лежит больший угол, и наоборот.
Рис. 9. Тупоугольный треугольник
2. Против равных сторон лежат равные углы, и наоборот.
Рис. 10. Тупоугольный треугольник с равными боковыми сторонами
3. Сумма углов тупоугольного треугольника равна 180°.
4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:


















