вопрос чему равна площадь параллелограмма
Площадь параллелограмма — формула, методика и примеры вычисления
Задачи на нахождение площади параллелограмма довольно часто встречаются в геометрии при выполнении контрольных работ, написании зачетов и решении практических заданий экзаменационных билетов. Для получения отличных оценок необходимо знать доказательства теорем, основные соотношения и методику их нахождения, а также уметь применять знания, полученные в процессе обучения, на практике.
Общие сведения
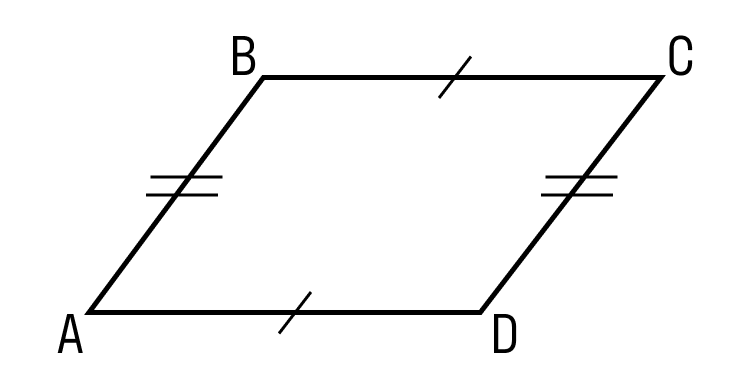
Перед обучением решению задач специалисты рекомендуют изучить теорию и разобраться в ней. Параллелограмм — геометрическая фигура, состоящая из четырех вершин и взаимно-параллельными, а также равными между собой противоположными сторонами. Высота — часть прямой (отрезок), исходящая из вершины на противоположную сторону и образующая с последней прямой угол.
Диагонали не равны между собой. Для удобства их обозначают литерами F и f (большая и малая соответственно). Однако у квадрата и прямоугольника они эквивалентны. Специалисты рекомендуют на начальных этапах обучения правильно определять геометрическую фигуру. Для этой цели существуют признаки параллелограмма.
Признаки параллелограмма
Признаки — набор критериев и правил, при помощи которых определяется тип геометрического тела. В некоторых задачах с повышенной сложностью дается четырехугольник с определенными исходными данными. Далее необходимо найти один из его параметров по формуле. Для этого следует правильно идентифицировать фигуру, чтобы воспользоваться необходимым соотношением.
Вот на этом этапе будут полезны признаки, позволяющие отнести геометрическое тело к классу параллелограммов. К ним относятся следующие:
Следует отметить, что при выполнении одного условия фигура принадлежит к классу параллелограммов.
Свойства фигуры
Свойства — утверждения, доказанные математиками. Они применяются для доказательств теорем, решения диофантовых (линейных) систем уравнений на нахождение двух неизвестных величин, вычисления параметров фигуры, а также для проектирования деталей. Для этих целей можно применять такие утверждения:
После свойств математики рекомендуют ознакомиться с некоторыми теоремами, позволяющими выводить формулу площади параллелограмма.
Теоремы о площади
Формулы площади — базовые соотношения, позволяющие найти другие параметры параллелограмма. Однако начинающему математику рекомендуется посмотреть, каким образом они доказываются. В отличие от прямоугольника величина рассчитывается немного иначе. Формулы — математическая запись определенной теоремы про площадь. Их всего три:
Однако для удобства доказательства утверждений следует ввести обозначения основных параметров фигуры:
Следует отметить, что специалисты при решении любой задачи или доказательстве геометрических тождеств рекомендуют использовать сокращенные записи. Этот подход является признаком мастерства и правилом хорошего тона в точных науках.
Сторона и высота
Первую теорему можно сформулировать следующим образом: площадь параллелограмма равна произведению большей стороны на значение высоты. Доказывается утверждение довольно просто по такому алгоритму:
Следующая теорема имеет такую формулировку: при известных сторонах параллелограмма и размерности угла между ними его площадь эквивалентна произведению первых двух на синус третьего, то есть S=k*l*sin (∠v). Доказывается утверждение по такой методике:
Утверждение доказано. Следует отметить, что в геометрии очень часто одна теорема используется для доказательства другой.
Величины диагоналей
Третья теорема определения величины площади параллелограмма через диагонали имеет следующую формулировку: размерность эквивалентна произведению диагоналей на острый угол между ними (S=F*f*sin (∠z)). Доказывается утверждение по такому алгоритму:
Следует отметить, что результирующая формула с подстановкой всех величин имеет следующий вид: S=[(Ff/2)]*sin (∠z). Однако для решения задач возможно использовать еще один параметр, который называется периметром.
Информация о периметре
Периметр или поверхность плоского геометрического тела — алгебраическая сумма сторон параллелограмма. Он обозначается литерой «Р». Базовое соотношение имеет следующий вид: S=MN+NO+OP+MP=2 (k+l). Кроме того, существуют другие соотношения для определения Р:
Следует отметить, что из этих соотношений можно найти стороны, высоту и углы. Кроме того, последнее соотношение можно записать в другом виде: P=2[k+H/sin (z)]=2[l+H/cos (v)]. Эти формулы строятся на основании теорем о площади параллелограмма, в которых стороны и другие параметры выражаются через S треугольников. Специалисты рекомендуют после изученного материала переходить к рассмотрению других соотношений.
Другие параметры
Определение сторон и диагоналей осуществляется посредством следствий из теорем. Математики рекомендуют воспользоваться готовыми формулами, но не стоит забывать и о тренировках. Последние реализуются при помощи самостоятельного выражения одной величины через другую. Стороны можно найти, когда известны следующие параметры:
Для нахождения диагонали специалисты рекомендуют также воспользоваться следствием из последней теоремы. Кроме того, возможности расчетов расширяются при использовании и других соотношений:
Для практического применения знаний специалисты рекомендуют переходить к заданиям по геометрии.
Пример решения
Для закрепления теоретических знаний рекомендуется постоянно решать задачи. Условие одной из них имеет следующий вид:
Необходимо найти площадь (S), высоту (H). Вычисляются необходимые параметры по следующему алгоритму:
Задачу можно решать при помощи других соотношений. Однако это приведет к увеличению количества вычислений, в результате которых могут возникнуть ошибки.
Таким образом, для нахождения площади параллелограмма нужно знать признаки фигуры, свойства, теоремы, формулы и соотношения, а также чаще решать различные задачи.
Площадь параллелограмма
Геометрия — один из наиболее сложных разделов школьного курса математики. Причина такой сложности состоит в том, что для решения геометрических задач часто требуются нестандартные подходы и пространственное мышление.
При это очень мало стандартных алгоритмов, к которым привыкли школьники. Приходится думать с опорой на теоретический багаж, причем довольно простые формулы часто не приходят ученику в голову там, где должны автоматически всплывать подсказки. Одной из таких формул является выражение для определения площади параллелограмма, о которой и пойдет речь в этой статье.
Площадь параллелограмма — сколько их?
Площадь геометрических фигур издавна интересовала людей, как прикладной объект. Уже древние египтяне были довольно хороши в соответствующих подсчетах, потому что их вынуждала окружающая действительность. Землемеры и сборщики налогов интересовались площадями не для решения школьных задач и не для получения высокого балла на ЕГЭ. Их интерес был более приземленным:
Эти простые вопросы приблизили человечество к современной науке и те сложные понятия, которыми оперируют математики, до сих пор базируются на простых формулах. В этом ряду площадь параллелограмма занимает особенное место, потому что это универсальная геометрическая фигура, частными случаями которой являются:
Даже треугольник — просто половина параллелограмма, что делает операции с этой фигурой важной частью базовых знаний. Давайте вспомним ее основные свойства:
С параллелограммом связано несколько интересных формул и площадь — в их числе. Этот параметр можно найти несколькими способами, которые мы подробно изучим ниже с примерами.
Площадь параллелограмма по стороне и высоте
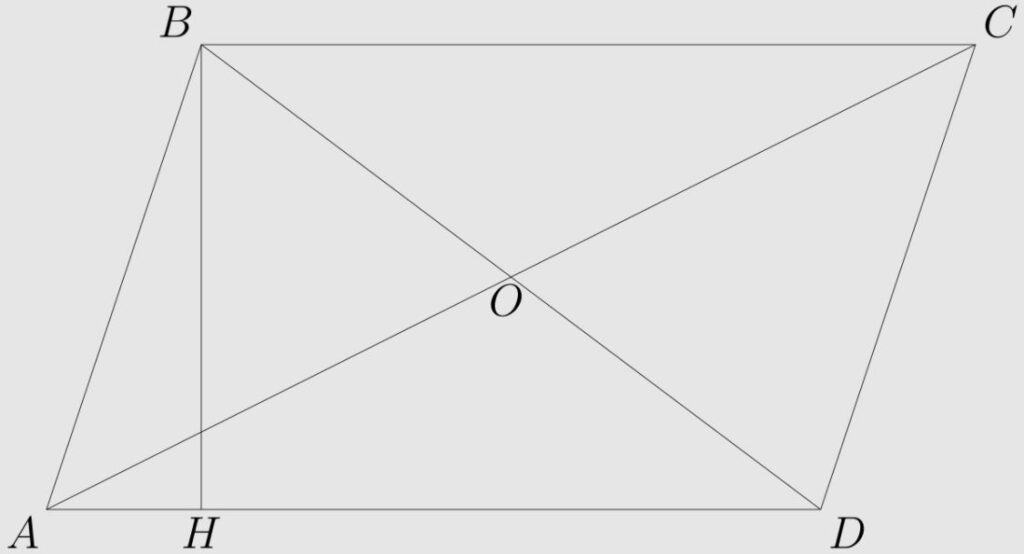
У нас есть параллелограмм АВСD, из вершины которого на противоположную сторону опущена высота ВН, пересекающая АD под прямым углом. Площадь фигуры АВСD равна произведению стороны АD на ВН.
Решение
Запишем выражение для нахождения площади:
Выразим из нее ВЕ и подставим значения из условия:
ВЕ = S АВСD / СD = 50 / 5 = 10 см.
Площадь параллелограмма по сторонам и углу между ними
Формулировка: площадь параллелограмма равна произведению двух сторон параллелограмма на синус угла между ними.
S АВСD = AB x AD х sin ∠BAD = AB x AD х sin ∠ABC.
Решение
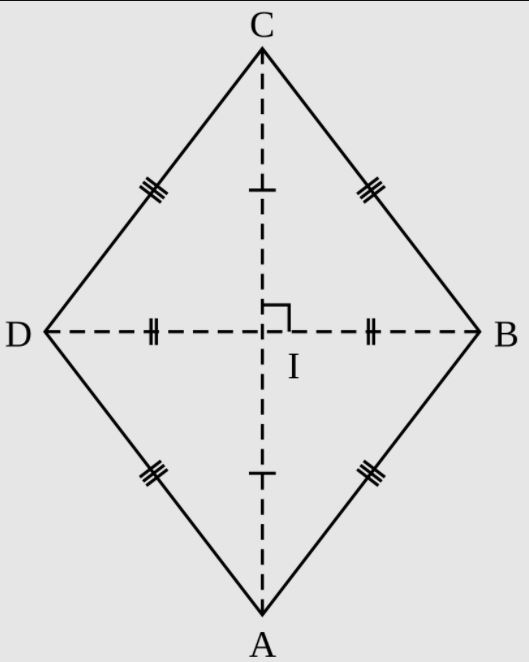
Поскольку ромб — это частный случай параллелограмма, воспользуемся соответствующей формулой:
S АВСD = AB x AD х sin ∠BAD.
В этом уравнении нам известна площадь и угол. Поскольку стороны ромба равны, то преобразуем выражение следующим образом:
Подставим значения из условия:
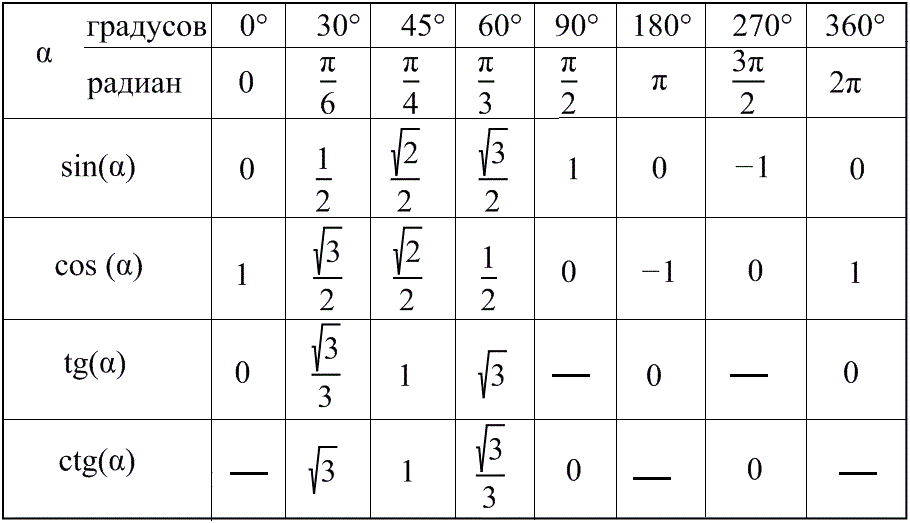
Значение синуса посчитаем на калькуляторе, выберем из таблицы Брадиса (для тех, кто помнит этого прекрасного человека) или из представленной в этой статье таблицы. В итоге выражение преобразуется следующим образом:
Выразим из этого выражения АВ:
Площадь параллелограмма по диагоналям и углу между ними
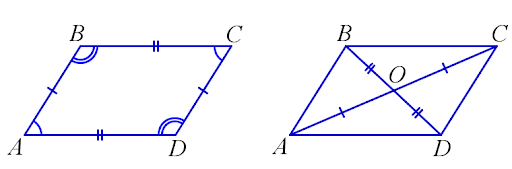
Формулировка: площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
S АВСD = ½ AС x ВD х sin ∠BОС = ½ AС x ВD х sin ∠BОА
Пример 3. Дан параллелограмм АВСD, диагонали которого равны по 20 см, а угол между ними составляет 90 градусов. Найти площадь треугольника АВD.
Решение
Заметим, что площадь треугольника АВD, который образуется путем деления параллелограмма АВСD его диагональю АD составляет половину площади самого параллелограмма. Это следует из равенства треугольников АВD и АСD по трем сторонам:
Запомним это и перейдем к поискам площади параллелограмма:
S АВСD = ½ AС x ВD х sin ∠BОС.
Подставим в эту формулу значения из условия:
S АВСD = ½ х 20 x 20 х sin 90°.
Значение синуса выберем из предыдущей таблицы: