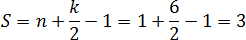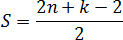вершины многоугольника лежат в узлах координатной сетки что это

Метод узлов

Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!

Для начала введем новое определение:

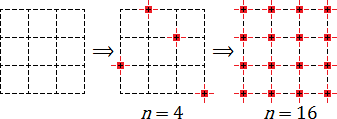
— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.

Обозначение

На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.

Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:

Теорема

Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:

где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).

Задача:

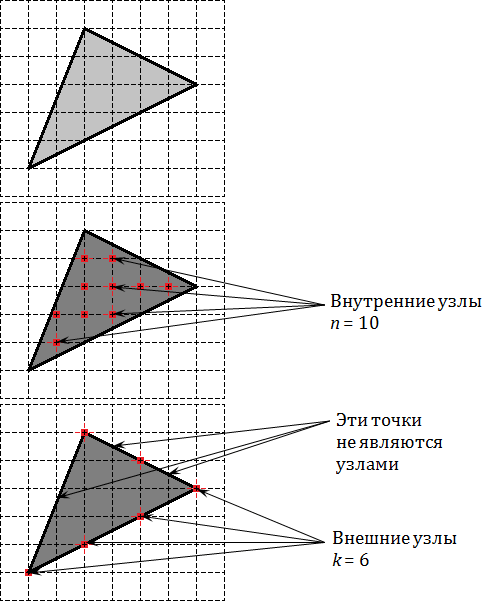
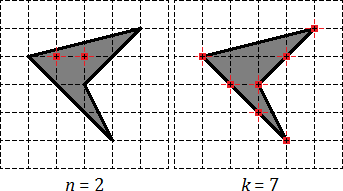
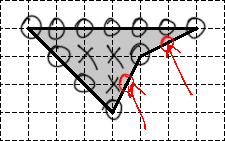
Рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.

На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего

Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.

С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.

Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются

Посмотрим, как все это работает в настоящих задачах.

Задача 2:

Найдите площадь треугольника, если размер клетки равен 1 x 1 см:

Решение

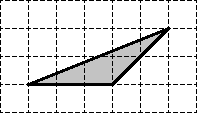
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:

Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.

Теперь считаем площадь по формуле:

Вот и все! Задача решена.

Задача 3:

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.

Решение

Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.

Остается подставить числа в формулу площади:

Ответ: 4,5

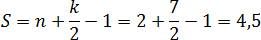
Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.

Важное замечание по площадям

Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:

Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:

Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»:

Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!

Сегодня мы научились считать площади фигур в задаче B5 методом узлов. Повторим, что для начала введят два определения:

Давайте посмотрим, как эти узлы выглядят на конкретной фигуре в задаче B5

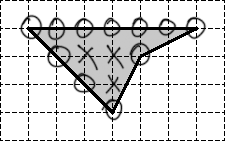
Задача. Найдите площадь четырехугольника изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Крестиками обозначены внутренние узлы. Очевидно, их количество Кружками обозначены граничные узлы. Их общее количество равно

Обратите внимание: под узлами подразумеваются только те точки, которые лежат на пересечении горизонтальных и вертикальных линий нашей сетки. Другими словами, следующие две точки не являются узлами, хотя в них граница фигуры также пересекается с линиями сетки:

Переходим к решению задачи. Для того, чтобы решать задачи B5 ЕГЭ по математике методом узлов, вам потребуется запомнить следующую теорему:

Теорема. Пусть дана фигура с внутренними узлами и граничными узлами. Тогда площадь этой фигуры считается по формуле:

S = n + 0,5 k − 1

Вот так все просто! Главное — запомните, это число внутренних узлов, число граничных узлов.

В нашем случае мы уже подсчитали, что Подставляем полученные числа в формулу и получаем:

Мы получили ответ: площадь четырехугольника

Ответ: 7,5

Как видите, задача свелась практически к устному счету. Поэтому обязательно возьмите данный прием на вооружение, ведь велика вероятность того, что на настоящем ЕГЭ по математике вам попадется именно такая задача B5 — площадь фигур на координатной сетке.

Источник

Клетка и вычисление площади

Россия, г. Иркутск, МБОУ города Иркутска СОШ №11

с углублённым изучением отдельных предметов

СОДЕРЖАНИЕ

Теоретическая часть Историческая справка…………………………………………………стр.3 Формула Пика………………………………………………………….стр.3 Узлы на отрезке………………………………………………………..стр.7 Практическая часть Решение задач………………………………………………………….стр.9 Игры на клетчатой бумаге…………………………………………. стр.12 Заключение……………………………………………………………….стр.14 Список литературы………………………………………………………стр.15 Приложения……………………………………………………………стр.16

Выполняя задания для подготовки к математическому конкурсу, мне встретилась задача, для решения которой потребовалось много времени. Вот условие этой задачи:

Введите на клетчатой бумаге систему координат. Отметьте точки А(-2;7), В(1;-2), С(-4;-7), Д(2;-5), Е(3;-8), F(5;-4), G(14;-1), Н(8;2), К(11;8), L(6;3) и соедините их последовательно отрезками АВ, ВС, СД, ДЕ, ЕF, FG, GH, НК, KL, LA. Найдите площадь полученной фигуры.

Учитель математики мне предложила один из выпусков серии «Библиотечка клуба «Кенгуру». В нем рассказывается о формуле Пика, которая позволяет находить площади любых многоугольников с вершинами в узлах клетчатой бумаги.

Мой проект посвящен клетчатой плоскости, то есть бесконечному листку бумаги, расчерченному на квадратики. Казалось бы, что увлекательного можно найти на обыкновенном клетчатом листочке? Не судите поспешно!

Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Я научилась вычислять площади многоугольников, нарисованных на клетчатом листке. Для многих задач на бумаге в клетку нет общего правила решения, конкретных способов и приёмов. Вот это их свойство обуславливает их ценность для развития не конкретного учебного умения или навыка, а вообще умения думать, размышлять, анализировать, искать аналогии, то есть, эти задачи развивают мыслительные навыки в самом широком их понимании.

Предмет исследования: задачи на вычисление площади многоугольника на клетчатой бумаге, методы и приёмы их решения.

Методы исследования: моделирование, сравнение, обобщение, аналогии, изучение литературных и Интернет-ресурсов, анализ и классификация информации.

Цель исследования: вывести и проверить формулы вычисления площадей геометрических фигур с помощью формулы Пика.

Для достижения поставленной цели предусматриваем решение следующих задач:

Изучить литературу по данной теме; Рассмотреть различные способы вычислений площадей многоугольников; Показать практическое применение этих способов; Выяснить преимущества и недостатки каждого способа; Систематизировать и углубить накопленные мной знания; Повысить качество знаний и умений.

Многообразие задач на бумаге в клеточку, их «занимательность», отсутствие общих правил и методов решения вызывают у школьников затруднения при их рассмотрении

Гипотеза: Площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по формуле планиметрии.

При решении задач на клетчатой бумаге нам понадобится геометрическое воображение и достаточно простые геометрические сведения, которые известны всем.

Австрийский математик Георг Александер Пик родился 10 августа 1859 году в Вене. Его отец, будучи руководителем частного института, предпочел до 11 лет обучать мальчика на дому, а потом отдал его сразу в четвертый класс гимназии, окончив которую в 1875 году, поступил в Венский университет.

В 1900-1901 годах был деканом философского факультета Карлова университета, и в 1911 году Пик оказался во главе комиссии, которая приняла на кафедру математической физика Альберта Эйнштейна. Они становятся близкими друзьями, совершая продолжительные пешие прогулки и беседуя, вместе музицируют.

Среди всего многообразия достижений австрийского математика выделяется формула для вычисления площадей многоугольников с вершинами в узлах клетки. Она стала широко известна только в 1969 году,

после того, как Гуго Штейнгауз включил ее в свою знаменитую книгу «Математический калейдоскоп».

После выхода в 1927 году на пенсию Пик вернулся в свой родной город Вену. Однако после аншлюса (присоединение) 12 марта 1938 года Австрии с Германией ему снова пришлось перебраться в Прагу. В сентябре 1938 года фашистская Германия вторглась на территорию Чехословакии. был брошен в концентрационный лагерь в Терзинштадте, где и умер две недели спустя.

Многоугольник без самопересечений называется решётчатым, если все его вершины находятся в точках с целочисленными координатами (в декартовой системе координат).

Найдем площадь многоугольника с вершинами в узлах (рис.1). Искать ее можно по-разному.

1 способ: с помощью палетки.

способ: попробовать разрезать многоугольник на достаточно простые фигуры, найти их площади и сложить. Однако, это очень хлопотно! способ: вычислю площадь заштрихованной фигуры (рис.2), которая «дополняет» многоугольник до прямоугольника АВСД, и вычту эту площадь из площади АВСД. Заштрихованная фигура (в отличие от исходного многоугольника) легко разбивается на прямоугольники и прямоугольные треугольники, так что ее площадь вычисляется без усилий. Она равна:

1·2+0,5·1·2+0,5·1·1+1·3+0,5·1·4+0,5·1·2+0,5·1·4+0,5·1·3=13 кв. ед.

Следовательно, площадь исходного многоугольника равна 5·6-13=17кв. ед.

Хотя многоугольник и выглядел достаточно просто, для вычисления его площади мне пришлось изрядно потрудиться. Оказывается, площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая площадь такого многоугольника с количеством узлов, лежащих внутри и на границе многоугольника.

Пусть дан некоторый решётчатый многоугольник, с ненулевой площадью. Обозначим его площадь через S; количество точек с целочисленными координатами, лежащих строго внутри многоугольника — через В; количество точек с целочисленными координатами, лежащих на сторонах многоугольника — через Г.

Тогда справедлива формула S=В+Г:2-1, которую открыл и доказал австрийский математик в 1899 году (1859-1943)

Доказательство проведу в несколько этапов: от самых простых фигур до произвольных многоугольников:

Единичный квадрат. В самом деле, для него S=1, В=0, Г=4, и формула верна.

2.Прямоугольник со сторонами, параллельными осям координат. Для доказательства формулы обозначу через а и b длины сторон прямоугольника.

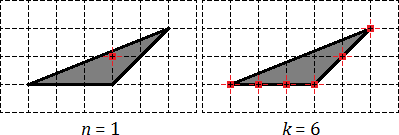
3.Любой треугольник, расположенный на клетчатой бумаге, внутри которого нет узлов, а на его границе узлами являются только вершины треугольника, имеет площадь 0,5 кв. ед. Такие треугольники называются примитивными. Следовательно, справедливо следующее утверждение:

Все примитивные треугольники равновелики и их площади равны половине площади единичного квадрата.

Множество примитивных треугольников разнообразно.

4.Прямоугольный треугольник с катетами, параллельными осям координат. Для доказательства замечу, что любой такой треугольник можно получить отсечением некоторого прямоугольника его диагональю. Обозначу через c число целочисленных точек, лежащих на диагонали. Формула Пика выполняется для такого треугольника, независимо от значения c.

5.Произвольный треугольник. Замечу, что любой такой треугольник может быть превращён в прямоугольник приклеиванием к его сторонам прямоугольных треугольников с катетами, параллельными осям координат (при этом понадобится не более 3 таких треугольников). Отсюда можно получить корректность формулы Пика для любого треугольника.

Остается сделать последний шаг: перейти от треугольников к многоугольникам

6.Произвольный многоугольник. Для доказательства разобью на треугольники с вершинами в целочисленных точках. Для одного треугольника формулу Пика я уже доказала. Дальше, можно доказать, что при добавлении к произвольному многоугольнику любого треугольника формула Пика сохраняет свою корректность. Отсюда следует, что она верна для любого многоугольника.

У меня возник вопрос: а всякий ли многоугольник с вершинами в узлах можно разрезать на такие треугольники?

Если все углы многоугольника меньше 180°, т. е. многоугольник выпуклый, то его можно разрезать на треугольники, например, проведя диагонали, соединяющие одну из его вершин со всеми остальными.

Следовательно, формула Пика верна для всех выпуклых многоугольников.

Опять вопрос: а выполняется ли формула Пика для невыпуклых многоугольников?

Доказательство этого факта оказалось слишком сложным. Я решила на конкретных примерах проверить формулу Пика для таких многоугольников.

S=0+32:2-1=15 кв. ед S=18+17:2-1=25,5 кв. ед S=0+20:2-1=9 кв. ед

1.3 УЗЛЫ НА ОТРЕЗКЕ

Если С1≠В, то смещу этот треугольник вдоль отрезка АВ на расстояние АС1. Получу равный ему треугольник С1С2Д2. Следовательно, С2- узел, и между С1 и С2нет узлов. Ясно, что если эту процедуру продолжить, то когда-нибудь в качестве очередной точки Ск+1 можно получить точку В – узел сетки. Рассматривая большой прямоугольный треугольник АRВ с гипотенузой АВ, прихожу к выводу:

АR=(k+1)АД1, ВR=(k+1)C1Д1, АВ=(k+1) АС1 (*)

1) Пусть числа p и q взаимно просты. Если между А и В были k узлов (k≥ 1), то, взяв ближайший узел к А узел С1, получу по формулам (*): p=( k+1)АД1, q=(k+1)C1Д1, т. е. p и q имеют общий делитель ( k+1), больший 1. Но ведь они взаимно просты.

Сколько клеток рассекает на две части диагональ прямоугольника m x n, где m и n взаимно простые числа?

Замечу, что диагональ такого прямоугольника не проходит через узлы. Буду считать, что диагональ идет из левого нижнего угла прямоугольника. Самой первой она рассекает левую нижнюю угловую клетку (клетку №1), потом она попадает в клетку №2 (рис.12), и так далее.

Пусть диагональ уже пересекла k клеток. Так как она ни разу не проходит через узел, то всегда можно однозначно указать, какую клетку она рассечет после клетки с номером k.

Пусть m и n-произвольные натуральные числа. Сколько клеток рассекает диагональ прямоугольника m x n?

2.1 РЕШЕНИЕ ЗАДАЧ

Введите на клетчатой бумаге систему координат. Отметьте точки А(-2;7), В(1;-2), С(-4;-7), Д(2;-5), Е(3;-8), F(5;-4), G(14;-1), Н(8;2), К(11;8), L(6;3) и соедините их последовательно отрезками АВ, ВС, СД, ДЕ, ЕF, FG, GH, НК, KL, LA. Найдите площадь полученной фигуры.

Используя формулы для вычисления площади прямоугольника и площади треугольника, вычислю площади фигур 1-16.

Источник

По математике на тему «Формула Пика».

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

4. Формула площади многоугольника через координаты вершин.

В истории черпаем мы мудрость,

Сюжет будет разворачиваться на обычном листке клетчатой бумаги.

Но тут нас ждёт много хлопот. Фигура легко разбивается на прямоугольники, трапеции, и треугольники, и её площадь вычисляется без усилий.

Хотя многоугольник и выглядит достаточно просто, для вычисления его площади придется изрядно потрудиться. А если бы многоугольник выглядел более причуд­ливо? Оказывается, площади многоугольни­ков, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с коли­чеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.

Вершины многоугольника (не обязательно выпуклого) расположены в узлах целочисленной решетки. Внутри его лежит В узлов решетки, а на границе Г узлов. Докажем, что его площадь равна В + – 1 (формула Пика).

Рассмотрим многоугольник, вершины которого находятся в узлах целочисленной решётки, то есть имеют целочисленные координаты.

Многоугольник разобьём на треугольники с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах.

n – число сторон многоугольника,

m – количество треугольников с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах,

В – число узлов внутри многоугольника,

Г – число узлов на сторонах, включая вершины.

Площади всех этих треугольников одинаковы и равны .

Следовательно, площадь многоугольника равна .

Теперь найдём эту сумму другим способом.

Тогда сумма углов с вершинами во всех внутренних узлах равна 360 0 В.

Общая сумма углов при узлах на сторонах, но не в вершинах равна 180 0 (Г – n).

Общая сумма углов всех треугольников равна 360 0 В + 180 0 (Г – n) + 180 0 (n – 2).

Таким образом, 180 0 m = 360 0 В + 180 0 (Г – n) + 180 0 (n – 2),

180 0 m = 360 0 В + 180 0 Г – 180 0 n + 180 0 n – 180 0 ·2,

откуда получаем выражение для площади S многоугольника:

известное как формула Пика.

На рисунке: В = 24, Г = 9, следовательно, S = 24 + – 1 = 27,5.

Найдём площадь первого многоугольника по формуле Пика:

В = 28 (зеленые точки);

Получаем, S = = 37 кв.ед.

Каждому многоугольнику M с вершинами в узлах целочисленной решетки поставим в соответствие число f (M) = , где суммирование ведётся по всем узлам решётки, принадлежащим M, а угол определяется следующим образом: = для внутренней точки многоугольника, = для граничной точки, отличной от вершины, и – угол при вершине, если данный узел – вершина. Легко видеть, что f (M) = + = В + – 1. Остаётся проверить, что число f (M) равно площади многоугольника M.

Пусть многоугольник M разрезан на многоугольники M₁ и M₂ с вершинами в узлах решетки. Тогда f (M) = f (M₁) + f (M₂), поскольку для каждого узла углы складываются. Поэтому если формула Пика верна для двух из многоугольников M, M₁ и M₂, то она верна и для третьего.

Если M — прямоугольник со сторонами p и q, направленными по линиям решетки, то

f (M) = (p – 1)(q – 1) + = pq.

В этом случае формула Пика справедлива. Разрезав прямоугольник M диагональю на треугольники M₁ и M₂ и воспользовавшись тем, что f (M) = f (M₁) + f (M₂) и f (M₁) = f (M₂), легко доказать справедливость формулы Пика для любого прямоугольного треугольника с катетами, направленными по линиям решетки. Отрезав несколько таких треугольников от прямоугольника, можно получить любой треугольник.

Для завершения доказательства формулы Пика остается заметить, что любой многоугольник можно разрезать на треугольники непересекающимися диагоналями.

Связь между площадью фигуры и количе­ством узлов, попавших в эту фигуру, особенно ясно видна в случае прямоугольника.

Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещенной сетки, каждый из Г – 4 гра­ничных неугловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу

Докажем, что эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки.

Обозначим через S _м площадь многоуголь­ника М с вершинами в узлах, а через П _м – величину , где В _м – число узлов внутри М, а Г _м — число узлов на границе. Тогда формулу Пика можно записать в виде .

Доказательство формулы разобьем на не­сколько шагов.

Если многоугольник М с вершина­ми в узлах сетки разрезан на 2 многоугольни­ка М ₁ и М ₂ , также имеющих вершины только в узлах сетки, то . Пусть многоугольник М разрезан на много­угольники М ₁ и М ₂ с вершинами в узлах отрез­ком АВ. Все узлы, кроме тех, которые попадают на отрезок АВ, дают одинаковый вклад в левую и правую части формулы. Рассмотрим узлы, лежащие на отрезке АВ.

Если такой узел лежит между А и В (на­пример, С), то для многоугольника М он внутренний, а для многоугольников М ₁ и М ₂ – граничный. Поэтому его вклад в П _м равен 1, а в каждое из выражений и – по 0,5, то есть вклады такого узла в П _м и равны.

Поэтому вклад каждого из этих узлов в П _м равен 0,5 а в — единице. Значит, суммарный вклад узлов А и В в П _м равен 1, что на 1 меньше, чем их вклад в . Но , а .

Из общего «вклада» всех узлов П_м вычи­тается 1, а из вычитается 2, и это компенсирует разницу вкладов узлов А и В.

Итак, .

Если многоугольник М с вершинами в узлах сетки разрезан на два многоугольника М₁ и М₂ (тоже с вершинами в узлах) и формула верна для каких-то двух из многоугольников М, М₁, М₂, то она верна и для третьего многоугольника.

Пусть, например, она верна для М ₁ и М ₂ , то есть . Тогда (по первому шагу) , но (по перво­му шагу) последнее выражение равно П _м , а равенство и есть формула Пика.

Докажем формулу Пика для пря­моугольного треугольника с вершинами в узлах сетки и катетами, лежащими на линиях сетки.

Формула Пика верна для произволь­ного треугольника с вершинами в узлах сетки.

Рассмотрев рисунок, легко понять: любой такой треугольник можно получить, «отрезав» от некоторого прямоугольника со сторонами, идущими по линиям сетки, несколько прямо­угольников и прямоугольных треугольников с катетами на линиях сетки. А так как формула Пика верна для прямоугольников и прямоугольных треугольников, то (вспомним шаг 2) она верна и для исходного треугольника.

Мы доказали, что если многоугольник мож­но разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

Источник