верно ли что все диаметры окружности равны между собой
Все диаметры окружности равны между собой
Здравствуйте!
Помогите ответить, какие из следующих утверждений верны?
1) Все диаметры окружности равны между собой.
2) В трапеции диагонали пересекаются и при пересечении делятся пополам.
3) Один из углов треугольника всегда не превышает 60 градусов.
Спасибо!
Утверждение №1.
Все диаметры окружности равны между собой.
Ответ.
Утверждение является верным.
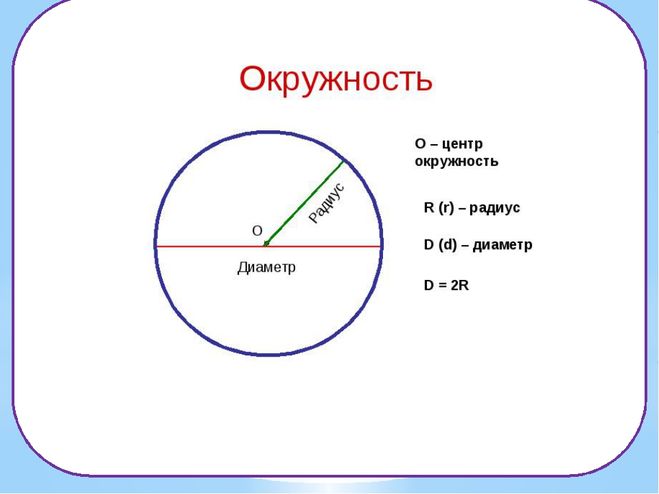
Диаметр окружности – это прямая, которая соединяет две точки окружности и проходит через ее центр.
Также диаметр равен двум радиусам. Как известно, длина всех радиусов окружности, как бы они не были проведены, является одинаковой. То же самое можно сказать и про диаметры окружности. Поэтому длины всех диаметров окружности будут равны один другому.
Утверждение №2.
В трапеции диагонали пересекаются и при пересечении делятся пополам.
Ответ.
Утверждение является неверным.
Существуют выпуклые четырехугольники, для которых будет справедливым данное утверждение. Этими фигурами являются прямоугольник, ромб и квадрат. Для трапеции справедливым является только первая часть утверждения – диагонали трапеции действительно пересекаются. Но чтобы они делились точкой пересечения пополам необходимо, чтобы основания трапеции были одинаковой длины, но тогда это будет уже другая геометрическая фигура.
Утверждение №3.
Хотя бы один из углов в треугольника всегда не больше 60 градусов.
Ответ.
Утверждение является верным.
В произвольном треугольнике наименьший угол всегда будет не большим 60 градусов.
Почему все диаметры окружности равны между собой?
Такое утверждает само классическое определение окружности- множество точек на плоскости, одинаково отстоящих от заданной точки- центра, не превышающих заданного расстояния- радиуса, а из другого определения, также знаем, что один диаметр равен двум радиусам если множество радиусов, то их легко превратить в диаметры.
Равенство всех диаметров окружности есть причина существования окружности.
Определение окружности: окружность представляет собой геометрической место точек расположенных на раодинаковом расстоянии от точки, называемой центром.
Расстояние до центра называется радиусом окружности.
Диаметр, по определению, равен двум радиусам, поэтому любые диаметры всегда будут равны между собой и равны:
Именно благодаря тому, что все диаметры равны. и получается окружность. Если бы они раличались по диаметру, то это было бы уже не окружностью, а овальностью. И если хотя бы один диаметр будет меньше, то это уже не будет окружностью.
Диаметры окружности равны между собой по определению окружности. Окружность-линия, состоящая из множества точек, равноудалённых(читай-на одинаковом радиусе) от центра окружности. Т.к. диаметр-это 2 радиуса, то и диаметры равны. Если вы хотите нарисовать фигуру, у которой разные диаметры, можете поискать информацию про овалы, кривые 2 порядка и эксцентриситет.
Циркуль-это чертёжный инструмент, который чертит окружности за счёт того, что рисующий грифель находится на одном и том же расстоянии от иголки, встроенной во вторую ножку циркуля.Конструктивно циркуль представляет собой две металлические ножки определённого размера, которые имеют свойство раздвигаться относительно точки их соединения.Поэтому один и тот же циркуль может чертить окружности от минимального размера до определённого максимального размера, определённого размером ножек циркуля.Если нужен больший размер для окружности, то необходимо менять циркуль на более крупный.Значение циркуля трудно переоценить.Все дуги, окружности рисуются только с помощью этого инструмента.Циркуль придумали скорее всего греки.
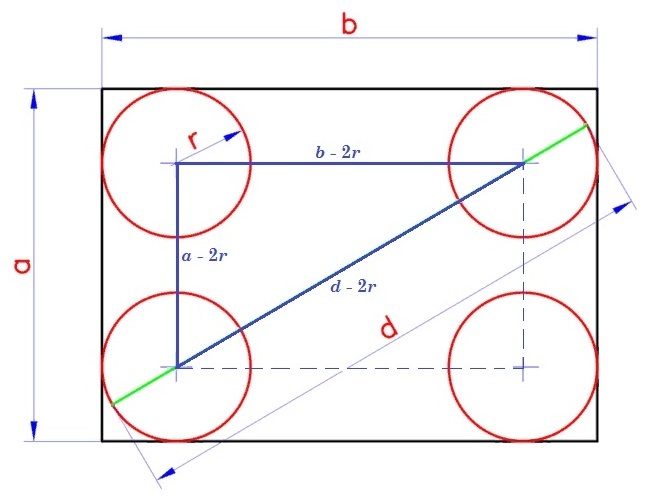
По теореме Пифагора:
(d − 2r)² = (a − 2r)² + (b − 2r)².
P.S. Не понятно, в чём проблема?
Ответ 2500 квадратный сантиметров. Поскольку радиус круга 25см, то сторона квадрата равна диаметру, то есть 2 радиуса, что равно 50см. Итого площадь квадрата равна 2500см. Вот если бы круг описывал квадрат, тогда сложнее, а тут все элементарно.
Верно ли что все диаметры окружности равны между собой
Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.
3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.
4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.» — неверно, вписанные углы, опирающиеся на одну и ту же хорду окружности, равны, если их вершины лежат по одну сторону от хорды.
2) «Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.» — неверно, окружности имеют две общие точки.
3) «Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.» — верно, если расстояние от центра окружности до прямой меньше радиуса, то прямая и окружность имеют две общие точки.
4) «Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.» — верно, вписанный угол измеряется половиной дуги,на которую он опирается.