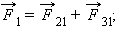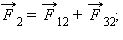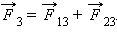в чем заключается принцип суперпозиции электрических полей
Принцип суперпозиции полей

Всего получено оценок: 92.
Всего получено оценок: 92.
Одним из важнейших принципов, существующих в электростатике, является принцип суперпозиции полей. Кратко рассмотрим суть этого принципа, выведем его математическую формулу.
Действие силового поля
Силовое поле – это особая форма материи, действие которого заключается в силовом влиянии на носители заряда. То есть, если у тела есть некоторый электрический заряд, и оно находится в силовом электрическом поле, то со стороны этого поля на тело будет действовать определенная сила, тем большая, чем больше напряженность поля.
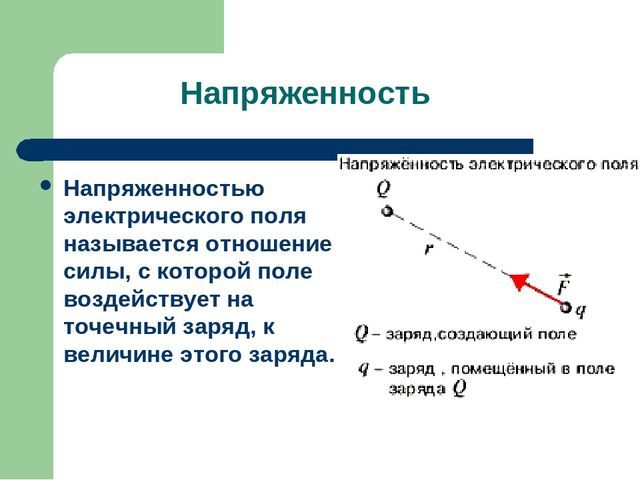
Природа поля не обязательно должна быть электрической. Действие гравитационного силового поля заключается в силовом воздействии на тела, имеющие массу (носители «гравитационного заряда»).
Сложение действия полей
Опыт показывает, что сила, действующая на заряд со стороны поля, не зависит от других сил, тоже действующих на заряд. При этом их источником могут являться другие поля. Фактически, несколько полей будут действовать на заряд независимо, каждое будет создавать силу, точно такую же, как если бы это поле в точке было бы единственным.
Таким образом, если заряд помещен одновременно в несколько электрических полей, он испытывает одновременное действие нескольких сил. А если на материальную точку действует несколько сил, то результатом их действия будет одна равнодействующая сила, которая находится векторным сложением исходных сил:
Сила, действующая на заряд, равна произведению напряженности поля на величину заряда:
Поскольку заряд в рассматриваемой ситуации один и тот же, то:
Принцип суперпозиции
Выражение в скобках представляет собой векторную сумму напряженностей всех полей, действующих на заряд. Получается, что результат действия на заряд нескольких полей эквивалентен действию одного поля, напряженность которого равна векторной сумме напряженностей всех полей, действующих на заряд. Иначе можно сказать, что результирующее поле, существующее в точке, является векторной суммой всех полей, его составляющих. В этом и состоит принцип суперпозиции (наложения) полей.
То есть, формула принципа суперпозиции полей записывается следующим образом:
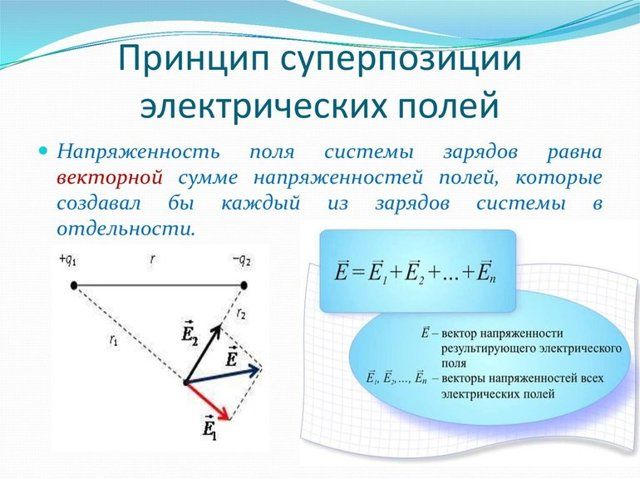
Отметим, что потенциал результирующего поля не обязательно равен сумме потенциалов исходных полей. Это происходит потому, что потенциал – скалярная величина, не учитывающая направление.
Принцип суперпозиции полей позволяет не только находить напряженность поля, создаваемые несколькими зарядами. Гораздо чаще возникает ситуация, когда заряд распределен по телу неравномерно. В этом случае тело можно разбить на множество элементарных тел, каждое из которых имеет свой заряд, отличный от прочих. А потом поле в любой точке пространства вычисляется, как векторная сумма полей всех элементарных зарядов. При уменьшении размера элементарного тела до нуля сумма заменяется интегралом по объему. Данный способ используется при определении картины картину сложных электрических полей, например, при проектировании электровакуумных приборов.
Принцип суперпозиции вовсе не так очевиден и универсален, как кажется на первый взгляд. Он действует лишь для линейных полей. Если поле нелинейно – принцип суперпозиции не работает. Примером нелинейного поля является поле сил трения. Если на тело действует несколько внешних сил, то, пока оно не сдвинется, сила трения равна векторной сумме отдельных составляющих. Но, как только тело сдвинулось, сила трения останется неизменной по модулю, даже если мы будем увеличивать количество действующих на тело сил.
Что мы узнали?
Принцип суперпозиции полей заключается в том, что результирующая напряженность поля, состоящего из нескольких исходных полей равна векторной сумме их напряженностей. Принцип суперпозиции выполняется для всех линейных полей, к числу которых относится и электрическое.
Принцип суперпозиции электрических полей
Одна из задач, которые ставит электростатика перед собой – это оценка параметров поля при заданном стационарном распределении зарядов в пространстве. И принцип суперпозиции является одним из вариантов решения такой задачи.
Принцип суперпозиции
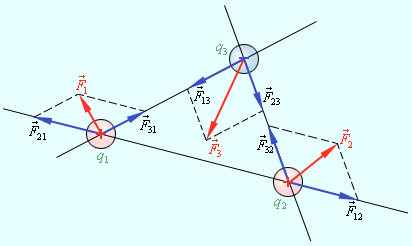
Предположим наличие трех точечных зарядов, находящихся во взаимодействии друг с другом. При помощи эксперимента возможно осуществить измерение сил, действующих на каждый из зарядов. Для нахождения суммарной силы, с которой на один заряд действуют два других заряда, нужно силы воздействия каждого из этих двух сложить по правилу параллелограмма. При этом логичен вопрос: равны ли друг другу измеряемая сила, которая действует на каждый из зарядов, и совокупность сил со стороны двух иных зарядов, если силы рассчитаны по закону Кулона. Результаты исследований демонстрируют положительный ответ на этот вопрос: действительно, измеряемая сила равна сумме вычисляемых сил согласно закону Кулона со стороны других зарядов. Данное заключение записывается в виде совокупности утверждений и носит название принципа суперпозиции.
Принцип суперпозиции:
Принцип суперпозиции полей заряда является одним из фундаментов изучения такого явления, как электричество: значимость его сопоставима с важностью закона Кулона.
При помощи принципа суперпозиции с использованием закона взаимодействия между точечными зарядами существует возможность определить силу взаимодействия между зарядами, присутствующими на теле конечных размеров. С этой целью каждый заряд разбивается на малые заряды d q (будем считать их точечными), которые затем берутся попарно; вычисляется сила взаимодействия и в заключение осуществляется векторное сложение полученных сил.
Полевая трактовка принципа суперпозиции
Полевая трактовка: напряженность поля двух точечных зарядов есть сумма напряженностей, создаваемым каждым из зарядов при отсутствии другого.
Для общих случаев принцип суперпозиции относительно напряженностей имеет следующую запись:
Инженерная практика подтверждает соблюдение принципа суперпозиции даже для очень больших напряженностей полей.
Все же следует также заметить, что в случае очень малых расстояний (порядка
Например, на поверхности тяжелых ядер при напряженности порядка
10 22 В м принцип суперпозиции выполняется, а при напряженности 10 20 В м возникают квантово-механические нелинейности взаимодействия.
Когда распределение заряда является непрерывным (т.е. отсутствует необходимость учета дискретности), совокупная напряженность поля задается формулой:
В этой записи интегрирование проводится по области распределения зарядов:
Принцип суперпозиции дает возможность находить E → для любой точки пространства при известном типе пространственного распределения заряда.
Примеры применения принципа суперпозиции
Решение
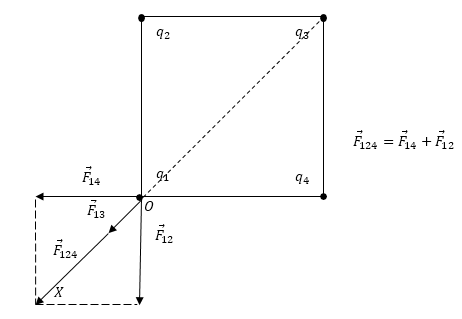
На рисунке 1 проиллюстрируем силы, влияющие на любой из заданных зарядов в вершинах квадрата. Поскольку условием задано, что заряды одинаковы, для иллюстрации возможно выбрать любой из них. Сделаем запись суммирующей силы, влияющей на заряд q 1 :
Силы F 12 → и F 14 → являются равными по модулю, определим их так:
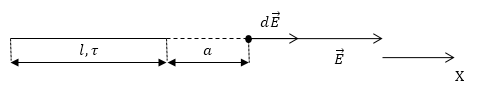
Задан электрический заряд, распределенный равномерно вдоль тонкой нити (с линейной плотностью τ ). Необходимо записать выражение, определяющее напряженность поля на расстоянии a от конца нити вдоль ее продолжения. Длина нити – l .
Решение
В заданной точке все векторы напряженности имеют одинаковую направленность вдоль оси ОХ, тогда:
Условием задачи дано, что заряд имеет равномерное распределение вдоль нити с заданной плотностью, и запишем следующее:
Подставим эту запись в записанное ранее выражение напряженности электростатического поля, проинтегрируем и получим:
Принцип суперпозиции электрических полей:
Одной из особенностей электрического поля является то, что в одной и той же точке пространства могут существовать поля различных источников и происхождения. При ном каждое из них сохраняет свои характеристики и не изменяется под действием остальных полей.
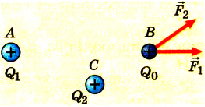
Пусть в некоторой точке А пространства находится некоторое тело с электрическим зарядом Q1 (рис. 1.7).
Если в произвольную точку В внесем точечное тело с положительным зарядом Q0, на него будет действовать сила F1 как результат взаимодействия заряда тела В с электрическим нолем тела А.
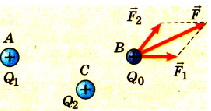
В произвольную точку пространства C внесем тело с зарядом Q2 (рис. 1.8). Его поле будет действовать на тело В с силой F2. Никаких изменений с силой F1 не произойдет. Но из механики известно, что если на тело действует несколько сил, то их можно заменить равнодействующей (рис. 1.9). Для случая нескольких сил


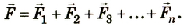
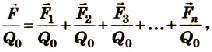
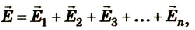
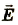 — напряженность поля системы всех тел;
— напряженность поля системы всех тел; 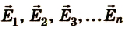 -напряжености поля каждого отдельного тела.
-напряжености поля каждого отдельного тела.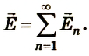
 и т. д., то результирующая напряженность поля в этой точке равна:
и т. д., то результирующая напряженность поля в этой точке равна:  .
.
 , созданная двумя точечными зарядами q1 и q2.
, созданная двумя точечными зарядами q1 и q2.

 . Об этом свидетельствует распределение силовых линий (рис. а), аналогичное распределению линий напряженности точечного заряда (рис. б).
. Об этом свидетельствует распределение силовых линий (рис. а), аналогичное распределению линий напряженности точечного заряда (рис. б).






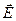 , созданного несколькими неподвижными точечными зарядами q1, q2. qn, равна векторной сумме напряженностей электрических полей
, созданного несколькими неподвижными точечными зарядами q1, q2. qn, равна векторной сумме напряженностей электрических полей 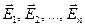 , которые создавал бы каждый из этих зарядов в той же точке наблюдения в отсутствие остальных:
, которые создавал бы каждый из этих зарядов в той же точке наблюдения в отсутствие остальных: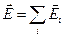 (1.5)
(1.5)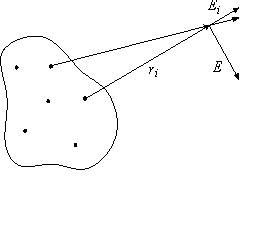
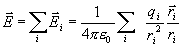 .
.