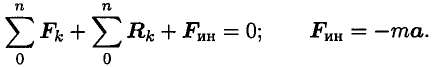в чем заключается принцип даламбера
Принцип кинетостатики (принцип Даламбера)
Принцип кинетостатики (принцип Даламбера)
Принцип кинетостатики используют для упрощения решения ряда технических задач.
Реально силы инерции приложены к телам, связанным с разгоняющимся телом (к связям).
Даламбер предложил условно прикладывать силу инерции к активно разгоняющемуся телу. Тогда система сил, приложенных к материальной точке, становится уравновешенной, и можно при решении задач динамики использовать уравнения статики.
Принцип Даламбера:
Материальная точка под действием, активных сил, реакций, связей и условно приложенной силы инерции находится в равновесии:
Порядок решения задач с использованием принципа Даламбера
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Принцип Даламбера — теоретическая механика
Принцип Даламбера: определение в теоретической механике
Принцип Даламбера – это один из главных принципов динамики, гласящий, что при добавлении силы инерции к воздействующим на точки механической системы активным силам и реакциям наложенных связей образуется сбалансированная совокупность сил. Другими словами, при сложении всех действующих сил, реакции связи и силы инерции получится ноль.
Принцип получил название в честь французского ученого Жана Даламбера, впервые изложившего данный закон в своем труде «Динамика». Второе название – принцип кинетостатики.
Формула
В записи рассматриваемый принцип выглядит следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
где i – это точка, на которую воздействуют активные силы F, наложенные реакции связи N и дополнительная сила инерции J.
Принцип для материальной точки
Согласно второму закону динамики, запишем:
\(m\overline a=\overline F+\overline N\)
где \(\overline N\) – наложенная реакция связи.
Сила инерции принимает значение:
\(\overline J=-m\overline a\)
\(\overline F+\overline N+\overline J=0\)
Данная формула описывает принцип Даламбера относительно материальной точки и расшифровывается так: в любой момент времени движения точки при сложении воздействующих на нее сил, реакций связи и силы инерции получается 0.
Принцип для механической системы
Для механической системы из n точек существует n уравнений следующего вида:
Суммируем все уравнения и введем векторные обозначения.
Главный вектор внешних сил:
Главный вектор реакций связей:
Главный вектор сил инерции:
В результате получится следующий вид:
\(\Sigma F_i+\Sigma N_i+\Sigma J_i=0\)
Чтобы твердое тело находилось в статичном состоянии, необходимо, чтобы главный вектор и главный момент действия сил были равны нулю. Учитывая это условие, а также теорему о моменте равнодействующей, получим такое соотношение:
\(\Sigma r_i\times F_i+\Sigma r_i\times N_i+\Sigma r_i\times J_i=0\)
Главный момент внешних сил:
\(\Sigma r_i\times F_i=M_0^F\)
Главный момент реакций связей:
\(\Sigma r_i\times N_i=M_0^N\)
Главный момент сил инерции:
\(\Sigma r_i\times J_i=M_0^J\)
Отсюда получим формулы:
\(\overline F^E+\overline N+\overline J=0\)
Таким образом, запись принципа кинетостатики для механических систем производится двумя формулами:
В любой момент времени движения механической системы главные векторы действующих сил, наложенных реакций связи и сил инерции дают в сумме 0.
Поскольку в образовавшихся формулах в силах инерции есть ускорение, эти формулы являются дифференциальными уравнениями – это вторая производная от закона движения точки.
Движение механической системы может быть записано в виде уравнения статики, позволяющие найти неизвестные силы и реакции связей.
Сила инерции Даламбера
Сила инерции – векторная величина, равная произведению массы и ускорения точки, направленная в противоположную сторону от ускорения. Данное понятие иначе называют силой Даламбера или даламберовой силой инерции.
Сила Даламбера представляет собой несуществующую в реальности величину, которую невозможно измерить. Она применяется в инерциональных системах отсчета для использования искусственного приема – упрощения уравнений динамики до уравнений равновесия.
Где применяется принцип
Принцип кинетостатики дает возможность записать движение произвольной системы в виде уравнения и решать задачи динамики с помощью методов равновесия. По этой причине рассматриваемый принцип широко используют в работе инженеры. Также принцип Даламбера удобен для нахождения неизвестных элементов уравнения.
Принцип Даламбера теоретической механики
Вы будете перенаправлены на Автор24
Принцип Даламбера является в теоретической механике одним из главных принципов динамики. Согласно этому принципу, при условии присоединения силы инерции к активно действующим на точки механической системы силам и реакциям наложенных связей, получается уравновешенная система.
Данный принцип получил название в честь французского ученого Ж. Даламбера, впервые предложившего его формулировку в своем сочинении «Динамика».
Определение принципа Даламбера
Принцип Даламбера звучит следующим образом: если к воздействующей на тело активной силе прикладывается дополнительная сила инерции, тело будет пребывать в равновесном состоянии. При этом суммарное значение всех действующих в системе сил, дополненное вектором инерции, получит нулевое значение.
Согласно указанному принципу, в отношении каждой i-той точки системы, становится верным равенство:
$ma$ при этом называется силой инерции Даламбера.
Готовые работы на аналогичную тему
Принцип Даламбера позволяет применять при решении задач динамики более упрощенные методы статики, что объясняет его широкое применение в инженерной практике. На этом принципе основывается метод кинетостатики. Особенно он удобен в применении с целью установления реакций связей в ситуации, когда известен закон происходящего движения или он получен при решении соответствующих уравнений.
Разновидностью принципа Даламбера выступает принцип Германа-Эйлера, фактически представлявшего собой форму данного принципа, но обнаруженную до появления публикации сочинения ученого в 1743 году. При этом принцип Эйлера не рассматривался его автором (в отличие от принципа Даламбера) в качестве основы для общего метода решения задач движения механических систем со связями. Принцип Даламбера считается более целесообразным в применении в случае необходимости определения неизвестных сил (для решения первой задачи динамики).
Принцип Даламбера для материальной точки
Многообразие типов решаемых в механике задач нуждается в разработке эффективных методик составления уравнений движения для механических систем. Одним из подобных методов, позволяющих посредством уравнений описать движение произвольных систем, считается в теоретической механике принцип Даламбера.
Опираясь на второй закон динамики, для несвободной материальной точки запишем формулу:
Эта формула является выражением принципа Даламбера для материальной точки, согласно которому, для движущейся в любой момент времени точки геометрическая сумма воздействующих на нее активных сил и силы инерции получает нулевое значение. Этот принцип позволяет записывать уравнения статики для движущейся точки.
Принцип Даламбера для механической системы
При суммировании всех этих уравнений и введении следующих обозначений:
которые являются главными векторами внешних сил, реакции связей и сил инерции соответственно, получаем:
Условием для равновесного состояния твердого тела является нулевое значение главных вектора и момента действующих сил. Учитывая это положение и теорему Вариньона о моменте равнодействующей в результате запишем такое соотношение:
примем следующие обозначения:
главные моменты внешних сил, реакции связей и сил инерции соответственно.
Эти две формулы являются выражением принципа Даламбера для механической системы. В любой момент времени для движущейся механической системы геометрическая сумма главного вектора реакций связей, внешних сил, и сил инерции получает нулевое значение. Также нулевой будет и геометрическая сумма главных моментов от сил инерции, внешних сил и реакций связей.
Полученные формулы являются дифференциальными уравнениями второго порядка из-за присутствия в каждом из них ускорения в силах инерции (второй производной закона движения точки).
Принцип Даламбера позволяет решать методами статики задачи динамики. Для механической системы можно записывать уравнения движения в виде уравнений равновесия. Из таких уравнений можно определить неизвестные силы, в частности, реакции связей (первая задача динамики).
Принципы Даламбера
К огда у генерала Детуша в Париже родился сын, сам он находился за границей по служебным обязанностям. А мать через несколько часов после рождения ребенка подбросила его на ступеньки церкви Сен-Жан-Лерон. Ребенок был так слаб, что комиссар полиции из жалости не отправил его в дом найденышей. Мальчика при крещении назвали Жаном Батистом Лероном и отдали в деревню кормилице. (Даламбером он впоследствии стал называть себя сам.) По всей вероятности, не одна только жалость руководила полицейским в этих заботах. Должно быть, он догадывался, что за ребенка будут платить, — и не ошибся. Детуш, вернувшись в Париж, начал наводить справки о сыне.
Забрав ребенка из деревни, отец решил найти ему кормилицу в Париже. Но мальчик был так слаб, что ни одна женщина не бралась его кормить. Наконец некая госпожа Руссо, жена стекольщика, сжалилась над отцом и над брошенным матерью бедным ребенком, согласилась взять его на свое попечение и обещала Детушу сделать все, чтобы сохранить жизнь его сыну. И ей удалось сдержать свое обещание.
Даламбер говорил, что отец часто навещал его у кормилицы, радовался его детской резвости, восхищался ответами сына, в которых видел проявление необыкновенного ума. И когда он отдал мальчика в школу, учителя вполне разделяли восторги отца.
Умирая, Детуш поручил Даламбера своему семейству; родные отца постоянно поддерживали с ним отношения; он часто ходил обедать к своим двоюродным сестрам и братьям. Незадолго до смерти отец поместил четырехлетнего мальчика в хороший пансион, и с этих лет Даламбер начал серьезно учиться.
В Коллеже Мазарини Даламбер прекрасно выучился всему, чему тогда учили; отлично знал по-латыни, а по-гречески настолько, что впоследствии мог читать в подлиннике Архимеда и Птолемея. В то время обращали большое внимание на развитие красноречия, и Даламбер вышел из школы замечательным оратором.
Физика, преподаваемая в то время, очень мало удовлетворяла строгий ум Даламбера. Впоследствии он постоянно смеялся над этой физикой и любил сочинять на нее остроумные пародии. Целью среднего образования в то время было научить рассуждать, говорить, сознательно читать и излагать более или менее удачно свои мысли письменно. Считалось, что дать фактическое знание не так важно, как развить уменье рассуждать, говорить и писать.
По окончании школы Даламбер опять поселился в семействе стекольщика Руссо и был рад помочь ему своими небольшими средствами. Он прожил в этой семье около сорока лет и привык к суровой простой жизни. Отсутствие тщеславия и привычка удовлетворяться в материальном отношении весьма немногим дали ему спокойствие и свободу деятельности — он не состоял на службе ни у государства, ни у частных лиц, хотя средства его были весьма ограниченны. Сам он писал уже в конце жизни: «Лишения с детства приучили меня довольствоваться малым; и то немногое, чем я располагаю, я готов разделить с добрыми, честными людьми, которые беднее меня».
Математика победила юриспруденцию
После школы Даламбер выдержал экзамен на степень бакалавра искусств, затем два года посещал академию юридических наук и вышел оттуда со званием лиценциата прав. Ему прочили славное будущее на поприще адвоката, но эта профессия сразу же пришлась Даламберу не по сердцу. Одновременно он для своего удовольствия занимался математикой. Даламберу едва исполнилось двадцать лет, когда он решил сделаться математиком, а в двадцать шесть он был уже светилом этой науки. В последние дни своей жизни Даламбер часто вспоминал те годы и говорил: «Математика — это моя самая старая любовь, самая верная возлюбленная!»
Занятия математикой скоро увенчались успехом. В 1739 и 1740 годах Даламбер представил в Парижскую академию наук два трактата о движении твердых тел в жидкостях и об интегральном исчислении и в 1741 году был избран адъюнктом академии.
Через два года, в 1743-м, выходит в свет его знаменитый «Трактат о динамике», послуживший поворотным пунктом в развитии механики. В нем был изложен известный «принцип Даламбера» как универсальный прием решения задач динамики системы со связями. Согласно ему, если к заданным (активным) силам, действующим на точки механической системы, и реакциям наложенных связей присоединить силы инерции, то получится уравновешенная система сил. В трактате впервые были сформулированы общие правила составления дифференциальных уравнений движения любых материальных систем.
Один из преемников Даламбера великий математик Лагранж, через пятьдесят лет написавший историю механики, говорил об этой книге, что она сразу положила конец путанице и хаосу, господствовавшим в этой отрасли науки.
Основным понятием динамики Даламбер считал движение. Он отрицательно относился к системе механики Ньютона. Даламбер говорил, что Ньютон «опирается только на расплывчатое и неясное положение, что действие пропорционально своей причине…», он «в механике бесполезен, и потому он должен быть из нее исключен». Понятие силы должно быть вообще исключено из механики, где следует основываться только на понятии движения. «Читатель не должен удивляться, — говорит Даламбер, — если я, исходя из этих соображений, так сказать, игнорирую “движущие причины” и рассматриваю исключительно движение, которое производится ими». В основе механики, по его мнению, лежат три основных положения: закон инерции, закон сложения движений и принцип равновесия.
В 1744 году Даламбер выпускает книгу «О равновесии и движении жидкостей», посвященную гидродинамике, в которой получает дальнейшее развитие труды Даниила Бернулли. Затем следует известный труд об интегральном исчислении, в котором автор получил ряд новых важных результатов.
Широкой известности Даламбера способствовала его книга «Исследования об общей причине ветров». За это произведение автор получил премию Королевской академии наук в Берлине и был избран ее членом. В нем он доказывал существование воздушных приливов — наряду с океанскими.
Даламбер внес серьезный вклад в развитие фундаментальных принципов современной механики, его труды вместе с работами Эйлера, братьев Бернулли и Клеро заложили основания математической физики. Ему принадлежат классические работы по задаче трех тел, нутации Земли, движению Луны, движению ветра, по теории музыки и др. Математические работы Даламбера основаны на принципе непрерывности Лейбница, позволившем ему ближе всего подойти к современному пониманию предела.
Несмотря на столь блестящие научные успехи, материальное положение Даламбера долгое время оставалось непрочным. Правда, в 1754 году покровительствовавший ему прусский король Фридрих II определил Даламберу небольшую пенсию, а еще через два года такое же пособие ему было назначено Людовиком XV. Полноправным же членом Парижской академии наук (с назначением содержания) Даламбер был избран только в 1765-м, но и тогда правительство долгое время не утверждало это решение академии, пока не было вынуждено уступить давлению научной общественности.
Несколько раз проваливали кандидатуру Даламбера и во Французской академии, членом которой он стал в 1754 году. А в 1772-м он был избран секретарем академии и занимал эту должность до своей кончины. (Французскую академию следует отличать от Парижской. Предметом деятельности первой была литература и филология, а второй — математика и естествознание.)
Красноречие Даламбера оказалось очень кстати во Французской академии. Новый член почти всегда открывал заседания, излагая какие-нибудь свои мысли, которые вели к оживленным прениям; большей частью он касался вопросов нравственности, поэзии или истории.
Даламбер был избран и во многие другие академии и научные общества. Членом Петербургской академии он был с 1764 года.
Энциклопедист
Велико было участие Даламбера в издании знаменитой «Энциклопедии», которая стал компендиумом всех идей эпохи Просвещения. Только один Дидро сделал для «Энциклопедии» больше. Вольтер, тоже бывший одним из деятельных сотрудников этого издания, писал Дидро и Даламберу: «Вы оба держите на плечах своих целый мир. Пока во мне не иссякнет последняя капля жизни, я буду всегда к услугам знаменитых авторов энциклопедии».
Это был грандиозный по своим масштабам труд, самый крупный и наиболее полный и систематизированный из существовавших до того времени. В нем предполагалось охватить всю совокупность тогдашних знаний. Большинство ее авторов и читателей рассматривали «Энциклопедию» как орудие борьбы против религиозных предрассудков, привилегий дворянства и духовенства, абсолютизма. Подавляющее большинство деятелей Французской революции можно назвать детьми «Энциклопедии». Вокруг «Энциклопедии» объединились все либеральные и радикальные слои французского общества того времени.
Даламбер написал «Введение к Энциклопедии», которое составило эпоху в интеллектуальной жизни сначала Франции, а потом и всего образованного мира. «Введение» было, в сущности, самостоятельным произведением, излагавшим философское кредо автора. В нем он изобразил происхождение и развитие человеческих знаний и дал собственную классификацию наук.
Даламбер вел в «Энциклопедии» отделы математики, физики и механики, он также поместил в ней множество статей по самым различным вопросам философии, истории, литературы, этики. Только в первом томе было свыше ста его публикаций. Среди них немало больших статей, по пять-десять страниц. Ряд статей Даламбера вызвал острую дискуссию, протесты французского духовенства, нападки и интриги противников идей Просвещения. Даламбер получил широкую известность, имел много друзей и врагов и приобрел репутацию вольнодумца, тем более что он был другом преследуемых Дидро и Вольтера.
После выхода седьмого тома «Энциклопедии», в 1757 году, Даламбер, устав от преследований и враждебности властей, был вынужден выйти из состава редакции, оставаясь, однако, сотрудником «Энциклопедии» и другом Дидро.
Выход в июле 1758 года сразу же запрещенного атеистического трактата «Об уме» Клода Адриана Гельвеция, единомышленника энциклопедистов, послужил поводом для приостановки издания «Энциклопедии». В королевском декрете говорилось, что польза «Энциклопедии» для прогресса наук и искусств не может компенсировать непоправимый вред, наносимый ею религии и общественной морали.
Возможно, издание так и не удалось бы довести до конца, но «Энциклопедия» имела высокопоставленных покровителей, как во Франции, так и за границей. Особую роль в этом сыграла российская императрица Екатерина II. Она обратилась с предложением к энциклопедистам перенести издание в Ригу или любой другой город России, если во Франции издание «сталкивается с какими-либо трудностями». Кроме того, зная о финансовых затруднениях издателей, она приобрела личную библиотеку Дидро, оставив ему книги в пользование как личному библиотекарю и выплатив ему жалованье за много лет вперед.
А поскольку Россия была союзницей Франции в Семилетней войне, то Франция была вынуждена считаться с мнением российской императрицы. Это позволило Дидро закончить издание энциклопедии во Франции.
Даламбер и Россия
Императрица не только дружила с Дидро, но и старалась привлечь к сотрудничеству других энциклопедистов. Она, в частности, пожелала поручить Даламберу воспитание своего единственного сына, цесаревича Павла Петровича. В 1762 году, перед поездкой в Берлин, Даламбер получил от Одара, библиотекаря Екатерины, письмо, в котором последний излагал ему эту просьбу императрицы. Но Даламбер отказался от этой чести. Великий ученый говорил о своем незнании людей и жизни, о сложности и трудности обязанностей воспитателя будущего повелителя такого обширного государства, как Россия.
Тем не менее начатая таким образом переписка Екатерины с Даламбером продолжалась до 1767 года довольно деятельно, но касалась исключительно литературных предметов, трудов Даламбера и занятий Екатерины по сочинению наказа Комиссии об уложении.
В 1782 году наследник русского престола, будучи в Париже и посетив Даламбера, выразил глубокое сожаление, что желание его матери не исполнилось. Прощаясь с Даламбером, Павел сказал: «Вы поймете, милостивый государь, как глубоко я сожалею, что мне не суждено было познакомиться с Вами ранее».
Но прошло еще несколько лет, и во Франции разразились революция, в теоретической подготовке которой энциклопедисты принимали столь деятельное участие. Тогда Екатерина, забыв о покровительстве, которое она некогда оказывала им и их «Энциклопедии», писала: «В этой книге было два лишь предмета: первый, уничтожение христианской религии, второй, — уничтожение царской власти».
Справедливости ради надо заметить, что Даламбер отказал не только Екатерине, но и прусскому королю Фридриху II, с которым он также долгое время состоял в переписке. Начиная с 1752 года Фридрих II неоднократно предлагал Даламберу стать президентом Берлинской академии наук, но ученый отвечал отказом.
Философ и публицист
Вольтер писал Даламберу: «Вы единственный писатель, который никогда не говорит ни больше того, ни меньше того, что хочет сказать. Я считаю Вас самым лучшим писателем нашего века». Вольтер признавал в манере Даламбера писать руку математика. Дидро считал Даламбера писателем тонким, остроумным, смелым, оригинальным, искренним, но упрекал его в том, что он о поэзии судит математически.
Сам Даламбер считал счастливейшим то время, когда занимался только математикой: тогда его знали лишь в ученом мире. Но «Введение» к «Энциклопедии» привлекло к Даламберу внимание публики, среди которой оказались и завистники, и враги. Он жаловался, что покой его нарушен с тех пор, как склонность его к литературе и философии перестала быть тайной его друзей.
В 1759 году Даламбер издал свои «Основы философии», которые стали продолжением и усовершенствованием философии Бэкона. Опираясь на его систему, Даламбер классифицировал науки, положив начало современному понятию «гуманитарные науки».
«Основы философии» заключают в себе также взгляды Даламбера на нравственность. Он возмущается несправедливым, неравномерным распределением земных благ между людьми, ставит в обязанность каждому довольствоваться малым, чтобы не захватывать принадлежащее другому.
Особую полемику вызвала его статья Essai sur les Gens de Lettres («Заметка о писателях»). В ней он говорит, что истинное мужество писателя состоит в борьбе с общественными предрассудками и пороками. Свобода, истина и бедность — эти три слова, по мнению Даламбера, всегда должны иметь перед глазами писатели, как люди, которым предстоит остаться в памяти потомков.
Разум должен принимать во внимание факты. Но при этом Даламбер считал, что в великой мировой загадке мы лишь «отгадываем некоторые слоги», точный смысл которых нам пока неизвестен.
Даламбер сомневался в существовании Бога, но не стал на позиции атеизма. В некоторой степени он признает значение откровения, которое, как он пишет во вступительной статье к «Энциклопедии», «могло иметь целью собрать воедино естественное знание обо всем, что нам необходимо знать: остальное для нас закрыто и, похоже, навсегда. Некоторые истины, в которые мы должны верить, немногие практические предписания — к этому сводится естественная религия». Несмотря на это, Даламбер — явный деист. Бог создает порядок во Вселенной, и мы разумом понимаем, что Он существует, на основании установленных Им неизменных законов, управляющих природой. По мнению Даламбера, Бог — Творец и Первопричина Вселенной, Он не вмешивается в повседневный естественный ход событий и человеческие поступки. Одним словом, религия не связана с моралью и не служит ей основой; нравственность есть и будет естественным, то есть рациональным качеством: «Нравственность — необходимое следствие образования общества, поскольку имеет целью то, что мы должны другим людям», — пишет Даламбер.
Болезнь и смерть
Даламбер умер 29 октября в 1783 году в Париже. Относясь к религии скептически, он и перед смертью не изменил своих взглядов и отказался от завершающего причастия. Парижский архиепископ запретил служить по нему заупокойную службу и отказал в месте на кладбище. Даламбера похоронили в общей могиле.
В своем «Эссе об обществе литераторов и о великих» Даламбер писал: «Счастливы те литераторы, которые пришли к выводу, что самый верный способ заставить себя уважать заключается в том, чтобы жить в согласии между собой и совершенно в стороне от великих… что благодаря взаимному согласию они без большого труда дойдут до того, что будут предписывать всей нации законы в вопросах вкуса и философии, что настоящее уважение есть то, которое оказывается нам по приговору тех людей, которые сами достойны уважения».