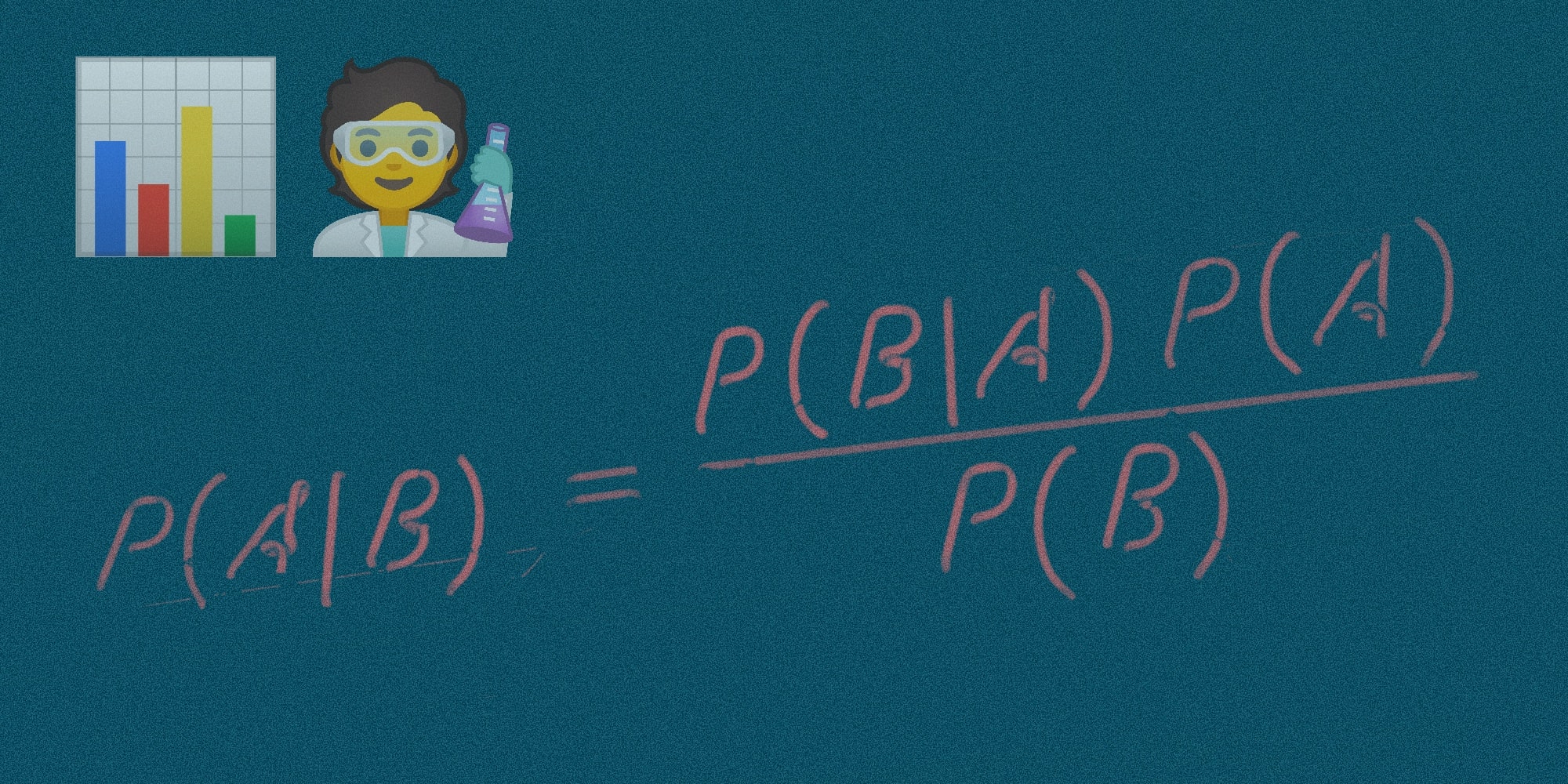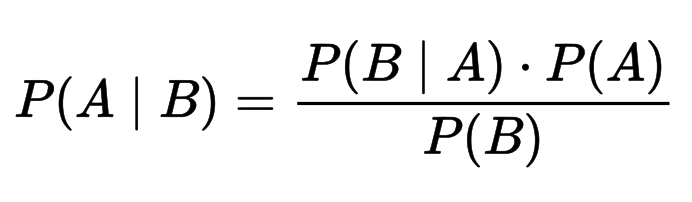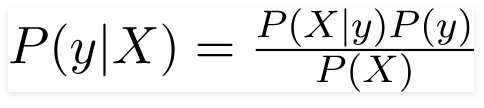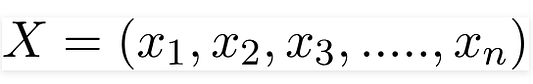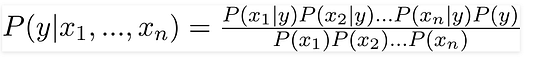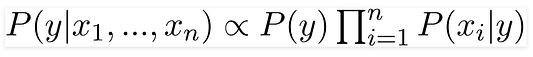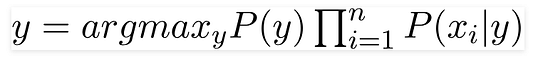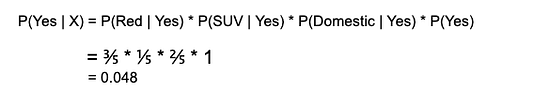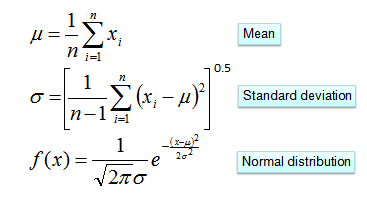в чем заключается наивность наивного байесовского классификатора
Наивный Байесовский классификатор в 25 строк кода
Наивный Байесовский классификатор один из самых простых из алгоритмов классификации. Тем не менее, очень часто он работает не хуже, а то и лучше более сложных алгоритмов. Здесь я хочу поделиться кодом и описанием того, как это все работает.
Немного теории
Пусть у нас есть строка текста O. Кроме того, имеются классы С, к одному из которых мы должны отнести строку. Нам необходимо найти такой класс с, при котором его вероятность для данной строки была бы максимальна. Математически это записывается так:
Вычислить P(C|O) сложно. Но можно воспользоваться теоремой Байеса и перейти к косвенным вероятностям:
Так как мы ищем максимум от функции, то знаменатель нас не интересует (он в данном случае константа). Кроме того, нужно взглянуть на строку O. Обычно, нет смысла работать со всей строкой. Намного эффективней выделить из нее определенные признаки (features). Таким образом формула примет вид:
Знаменатель нас не интересует. Числитель же можно переписать так.
Но это опять сложно. Здесь включаем «наивное» предположение о том, что переменные O зависят только от класса C, и не зависят друг от друга. Это сильно упрощение, но зачастую это работает. Числитель примет вид:
Финальная формула примет вид:

Т.е. все что нужно сделать, это вычислить вероятности P( C ) и P(O|C). Вычисление этих параметров и называется тренировкой классификатора.
Ниже — код на питоне. Содержит всего две функции: одна для тренировки (подсчета параметров формулы), другая для классификации (непосредственный расчет формулы).
В функции train первые пять строк производят подсчет количества классов C, а также частоту появления фич O и С в одном семпле. Вторая часть метода просто нормирует эти частоты. Таким образом на выходе получаются вероятности P© и P(O|C).
В функции classify происходит поиск наиболее вероятного класса. Единственное отличие от формулы (1) в том, что я заменяю произведение вероятностей на сумму логарифмов, взятых с отрицательным знаком, и вычисляю не argmax, а argmin. Переход к логарифмам — распространненный прием чтобы избежать слишком маленьких чисел, которые могли бы получится при произведении вероятностей.
Число 10(^-7), которое подставляется в логарифм, это способ избежать нуля в аргументе логарифма (т.к. он будет иначе он будет неопределен).
Чтобы натренировать классификатор возьмем размеченный список мужских и женских имен и воспользуемся этим кодом:
Файл ‘names.txt’ можно скачать здесь.
В качестве фич я выбрал последнюю букву имени (см функцию get_features). Работает неплохо, но для рабочего варианта лучше использовать схему посложнее. К примеру, выбрать первую букву имени и две последних. К примеру, вот так:
Алгоритм можно использовать для произвольного числа классов. К примеру, можно попробовать построить классификатор текстов по эмоциональной окраске.
🤖 Наивный байесовский алгоритм классификации: преимущества и недостатки
Alex Maszański
Что это такое?
Наивный Байес – это самый простой алгоритм, который вы можете применить к своим данным. Как следует из названия, этот алгоритм делает предположение, что все переменные в наборе данных «наивные», т.е. не коррелируют друг с другом.
Вы создаете алгоритм и вашей целью является проблема выше: классифицировать объект между мячом, ежиком и собакой. Сначала вы подумаете об определении символов объекта, а затем об их сопоставлении с объектами классификации, например, если объект – круг, то это будет мяч, если объект – колючее живое существо, то это будет ежик, а если наш объект лает, то, вероятно, это будет собака.
Причина проста: мы с детства видим зеленый шар, но собака или ежик такого цвета крайне маловероятны для нас. Таким образом, в нашем случае мы можем классифицировать объект, сопоставив его признаки с нашим классификатором по отдельности. Зеленый цвет был сопоставлен с ежом, собакой и мячом, и в итоге мы получили наибольшую вероятность принадлежности зеленого объекта к мячу. Это и есть причина, почему мы классифицировали его как мяч.
Теоретическая составляющая алгоритма
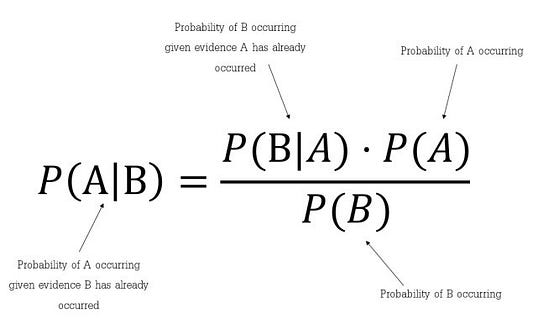
Теорема Байеса позволяет рассчитать апостериорную вероятность P(A | B) на основе P(A), P(B) и P(B | A).
Реализация на языке python
Результат работы кода:
Плюсы и минусы
В каких областях использовать?
Также этот алгоритм также хорошо известен благодаря функции многоклассового прогнозирования. Мы можем предсказать вероятность нескольких классов целевой переменной.
Таким образом, идеальные области для применения наивного байесовского классификатора это:
Из этого руководства вы узнали о наивном байесовском алгоритме классификации, его работе, проблемах, реализации, преимуществах и недостатках.
Несмотря на значительные успехи других методов за последние несколько лет, Байес все так же доказывает свою ценность. Он успешно применяется во многих приложениях, от текстовой аналитики и спам-фильтров до систем рекомендаций.
Что такое «наивный» в наивном классификаторе Байеса?
что наивного в наивном Байесе?
4 ответов
на самом деле есть очень хороший пример Википедии:
проще говоря, наивный классификатор Байеса предполагает, что наличие (или отсутствие) конкретного признака класса не связано с наличием (или отсутствием) любого другого признака, учитывая переменную класса. Например, плод можно считать яблоком, если он красный, круглый и около 4 дюймов в диаметре. Даже если эти особенности зависят друг от друга или от существования другого особенности, наивный классификатор Байеса считает, что все эти свойства независимо способствуют вероятности того, что этот плод является яблоком.
в принципе, это «наивно», потому что он делает предположения, которые могут оказаться или не оказаться правильными.
Это называется наивным, потому что он делает предположение, что все атрибуты независимы друг от друга. Это предположение, почему его называют наивным, поскольку во многих ситуациях реального мира это не подходит. Несмотря на это, классификатор работает очень хорошо во многих реальных ситуациях и имеет сопоставимую производительность с нейтральными сетями и SVM в некоторых случаях (хотя и не во всех).
для классификации когда мы находим совместное распределение, проблема заключается в том, что оно просто отражает данные обучения и также очень трудно вычислить. Поэтому нам нужно что-то, что обобщает более полезно.
на наивная модель обобщает сильно, что каждый атрибут распространяется независимо от любых других атрибутов.
Это действительно помогает не заботиться о зависимости между атрибутами в значительной степени.
🤖 Наивный байесовский алгоритм классификации: преимущества и недостатки
Alex Maszański
Что это такое?
Наивный Байес – это самый простой алгоритм, который вы можете применить к своим данным. Как следует из названия, этот алгоритм делает предположение, что все переменные в наборе данных «наивные», т.е. не коррелируют друг с другом.
Вы создаете алгоритм и вашей целью является проблема выше: классифицировать объект между мячом, ежиком и собакой. Сначала вы подумаете об определении символов объекта, а затем об их сопоставлении с объектами классификации, например, если объект – круг, то это будет мяч, если объект – колючее живое существо, то это будет ежик, а если наш объект лает, то, вероятно, это будет собака.
Причина проста: мы с детства видим зеленый шар, но собака или ежик такого цвета крайне маловероятны для нас. Таким образом, в нашем случае мы можем классифицировать объект, сопоставив его признаки с нашим классификатором по отдельности. Зеленый цвет был сопоставлен с ежом, собакой и мячом, и в итоге мы получили наибольшую вероятность принадлежности зеленого объекта к мячу. Это и есть причина, почему мы классифицировали его как мяч.
Теоретическая составляющая алгоритма
Теорема Байеса позволяет рассчитать апостериорную вероятность P(A | B) на основе P(A), P(B) и P(B | A).
Реализация на языке python
Результат работы кода:
Плюсы и минусы
В каких областях использовать?
Также этот алгоритм также хорошо известен благодаря функции многоклассового прогнозирования. Мы можем предсказать вероятность нескольких классов целевой переменной.
Таким образом, идеальные области для применения наивного байесовского классификатора это:
Из этого руководства вы узнали о наивном байесовском алгоритме классификации, его работе, проблемах, реализации, преимуществах и недостатках.
Несмотря на значительные успехи других методов за последние несколько лет, Байес все так же доказывает свою ценность. Он успешно применяется во многих приложениях, от текстовой аналитики и спам-фильтров до систем рекомендаций.
Наивный байесовский алгоритм
Введение
Самые простые решения обычно оказываются самыми действенными, и в этом смысле показателен пример наивного байесовского алгоритма. Несмотря на большие успехи машинного обучения в последние годы, наивный байесовский алгоритм остаётся не только одним из простейших, но и одним из самых быстрых, точных и надежных. Он успешно используется для многих целей, но особенно хорошо работает с задачами обработки естественного языка.
Наивный байесовский алгоритм — это вероятностный алгоритм машинного обучения, основанный на применении теоремы Байеса и используемый в самых разных задачах классификации. В статье разберём все основные принципы и понятия, связанные с наивным байесовским алгоритмом, чтобы у вас не осталось проблем с его пониманием.
Теорема Байеса
Теорема Байеса — это простая математическая формула, используемая для вычисления условных вероятностей.
Условная вероятность — это вероятность наступления одного события при условии, что другое событие (по предположению, допущению, подтверждённому или неподтверждённому доказательством утверждению) уже произошло.
Формула для определения условной вероятности:
Она показывает, как часто происходит событие A при наступлении события B, обозначается как P(A|B) и имеет второе название «апостериорная вероятность». При этом мы должны знать:
Вкратце можно сказать, что теорема Байеса — это способ определения вероятности исходя из знания других вероятностей.
Допущения наивного байесовского алгоритма
Основным допущением наивного байесовского алгоритма является то, что каждая характеристика вносит:
вклад в конечный результат.
Для лучшего понимания давайте рассмотрим пример. Это будет задача для автоугонщика.
Дано: параметры автомобиля (цвет, тип, страна производства).
Найти: угнана или нет (да или нет).
Пример
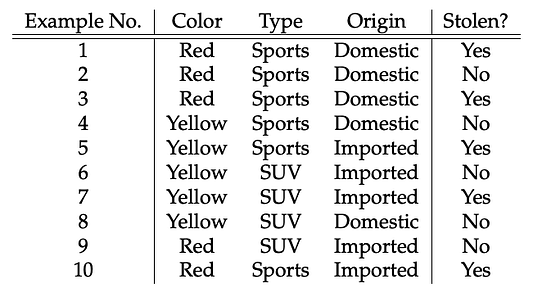
Все данные представлены в этой таблице:
Теперь мы можем оценить характер делаемых в рамках наивного байесовского алгоритма допущений с использованием данных нашего примера:
Примечание: допущения наивного байесовского алгоритма, как правило, некорректны в реальных ситуациях. Допущение о независимости всегда некорректно, но часто хорошо работает на практике. Поэтому алгоритм и называется наивным.
Вернёмся к таблице: здесь нам надо определиться с тем, какие машины угоняются, а какие — нет, исходя из параметров автомобилей. В столбцах у нас параметры машин, а в строках — варианты с разными сочетаниями этих параметров. Если мы возьмём первую строку, то увидим: цвет — красный, тип — спортивный, страна производства — местное производство. То есть угоняется спортивная машина красного цвета, произведённая в РФ. Хм… смотри-ка, научились делать!) Ах да, это же наивный алгоритм! Теперь попробуем решить, угоняется ли красный отечественный внедорожник. Вы когда-нибудь видели этого зверя? Вот и в нашей таблице такого варианта нет.
Для целей взятого нами примера давайте перепишем теорему Байеса. Ничего криминального: просто A и B заменим на y и X.
Переменная y — это переменная класса (последний столбик с ответом на вопрос, угоняется машина или нет при данных условиях). Переменной X обозначаются параметры/характеристики:
Здесь эти параметры x1,x2….xn могут представлять цвет, тип и страну производства. Подставляя X и используя цепное правило, получаем теорему Байеса вот в таком расширенном виде:
Теперь вы можете получить значения для каждого из параметров: просто берём данные и подставляем их в уравнение. Для всех вариантов сочетаний этих параметров знаменатель не меняется, он остаётся статичным. Так что его можно отбросить, введя в уравнение пропорциональность:
В нашем случае переменная класса (y) имеет только два результата: да или нет. А бывают случаи, когда классификация может быть многомерной. Поэтому надо найти переменную класса (y) с максимальной вероятностью.
Используя эту функцию, можно получить класс, исходя из имеющихся предикторов/параметров.
Апостериорная вероятность P(y|X) высчитывается так: сначала создаётся частотная таблица для каждого параметра относительно искомого результата. Затем из частотных таблиц формируются таблицы правдоподобия, после чего с помощью уравнения Байеса высчитывается апостериорная вероятность для каждого класса. Класс с наибольшей апостериорной вероятностью и будет прогнозируемым результатом. Ниже приведены частотные таблицы и таблицы правдоподобия для всех трёх предикторов.
В нашем примере три предиктора X:
Подставляя значения из приведённых выше таблиц в уравнение, вычисляем апостериорную вероятность P(Yes | X):
Так как 0,144 > 0,048, то для сочетания параметров RED SUV Domestic взятого нами примера (красного отечественного внедорожника) ответом на вопрос, угоняется ли машина, будет “нет”.
Проблема нулевой частоты
Одним из недостатков наивного байесовского алгоритма является то, что если класс и значение параметра не встречаются вместе, то оценка вероятности, высчитываемой с использованием частот, будет равна нулю. В итоге после перемножения всех вероятностей мы получим ноль.
В байесовской среде было найдено решение этой проблемы нулевой частоты: к каждой комбинации класса и значения параметра добавлять единичку, когда значение параметра нулевое.
Предположим, у нас есть такой набор данных:
Появляется нулевое значение, поэтому при вычислении вероятностей добавляем единичку к каждому значению этой таблицы:
Вот так мы избавляемся от нулевой вероятности.
Типы наивного байесовского классификатора:
Предполагается, что это гауссова правдоподобность характеристик, поэтому условная вероятность будет определяться следующим образом:
А что если в качестве характеристик будут числовые значения?
Одно из решений: перед тем как создавать частотные таблицы, нужно преобразовывать числовые значения в их категориальные аналоги. Другим решением, как было показано выше, может быть использование распределения числовой переменной с приблизительной оценкой частотности, близкой к истинной. Например, один из распространённых методов заключается в применении нормальных распределений или распределений Гаусса для числовых переменных.
Плотность распределения вероятностей для нормального распределения определяется двумя параметрами (среднее значение и среднеквадратическое отклонение) по формуле:
Практический пример: наивный байесовский классификатор с нуля на Python
Насущной проблемой для любого крупного веб-сайта сегодня становится всё возрастающий объём проникающей на эти сайты токсичной информации. Поэтому вполне естественно желание решить эту проблему, сделав популярные платформы типа Quora местом, где пользователи могут безопасно обмениваться друг с другом своими знаниями.
Quora — это платформа, которая дает людям возможность учиться друг у друга. Здесь можно задавать вопросы, общаться, обмениваться уникальными наработками и получать квалифицированные ответы. Главная задача — отсеять фейковые вопросы, то есть те, которые не имеют отношения к существу той или иной проблемы и делаются под какими-то ложными предлогами с намерением заявить о себе или просто попиариться, а не найти полезный ответ.
Цель — разработать модель классификации на основе наивного байесовского алгоритма, которая бы выявляла и помечала такие фейковые вопросы.
Набор данных можно взять отсюда. Загрузив набор данных для обучения и тестовые данные, можно приступать к выполнению задачи.
Посмотрим сначала, как выглядят реальные вопросы:
И мы можем увидеть, как выглядят фейковые вопросы:
Предварительная обработка текста
Следующий этап — это предварительная обработка текста перед разделением набора данных на данные для обучения и тестовые данные. Предварительная обработка включает в себя: удаление чисел, удаление знаков препинания в строке, удаление стоп-слов, стемминг (выделение основы слова) и лемматизацию (приведение словоформы к её базовой, словарной форме — лемме).
Построение наивного байесовского классификатора
Объединяем все методы предварительной обработки и создаём словарь слов и счётчик каждого слова в наборе данных для обучения:
Заключение
Наивные байесовские алгоритмы часто используются при анализе эмоциональной окраски текстов, фильтрации спама, в рекомендательных системах и т.д. Они легко и быстро внедряются, но их самый большой недостаток заключается в сложности соблюдения требования о независимости предикторов.