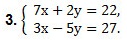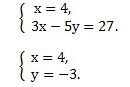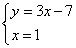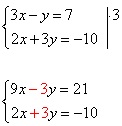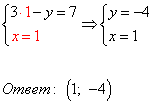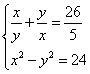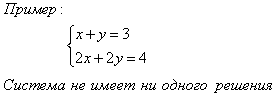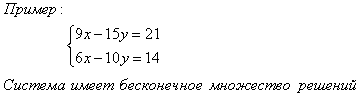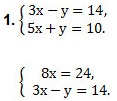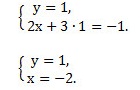в чем заключается метод сложения
Решение системы уравнений методом сложения
Этим видео я начинаю цикл уроков, посвящённых системам уравнений. Сегодня мы поговорим о решении систем линейных уравнений методом сложения — это один из самых простых способов, но одновременно и один из самых эффективных.
Способ сложения состоит из трёх простых шагов:
Если всё сделать правильно, то на выходе мы получим одно-единственное уравнение с одной переменной — решить его не составит труда. Затем останется лишь подставить найденный корень в исходную система и получить окончательный ответ.
Однако на практике всё не так просто. Причин тому несколько:
Чтобы получить ответ на эти вопросы, а заодно разобраться с несколькими дополнительными тонкостями, на которых «заваливаются» многие ученики, смотрите мой видеоурок:
Этим уроком мы начинаем цикл лекций, посвященный системам уравнений. А начнем мы из самых простых из них, а именно из те, которые содержат два уравнения и две переменных. Каждое из них будет являться линейным.
Системы — это материал 7-го класса, но этот урок также будет полезен старшеклассникам, которые хотят освежить свои знания в этой теме.
Вообще, существует два метода решения подобных систем:
Сегодня мы займемся именно первым методом — будем применять способ вычитания и сложения. Но для этого нужно понимать следующий факт: как только у вас есть два или более уравнений, вы вправе взять любые два из них и сложить друг с другом. Складываются они почленно, т.е. «иксы» складываются с «иксами» и приводятся подобные, «игреки» с «игреками» — вновь приводятся подобные, а то, что стоит справа от знака равенства, также складывается друг с другом, и там тоже приводятся подобные.
Как этого добиться и каким инструментом для этого пользоваться — об этом мы сейчас и поговорим.
Решение легких задач с применением способа сложения
Итак, учимся применять метод сложения на примере двух простейших выражений.
Задача № 1
Решаем простейшую конструкцию:
Прекрасно, мы нашли «икс». Что теперь с ним делать? Мы вправе подставить его в любое из уравнений. Подставим в первое:
Задача № 2
Здесь полностью аналогичная ситуация, только уже с «иксами». Сложим их:
Мы получили простейшее линейное уравнение, давайте решим его:
Важные моменты
Итак, только что мы решили две простейших системы линейных уравнений методом сложения. Еще раз ключевые моменты:
В следующих задачах мы рассмотрим прием вычитания, когда коэффициенты не противоположны.
Решение легких задач с применением метода вычитания
Задача № 1
Заметим, что противоположных коэффициентов здесь нет, однако есть одинаковые. Поэтому вычитаем из первого уравнения второе:
\[16x=32\left| :16 \right.\]
Задача № 2
Нюансы решения
Итак, что мы видим? По существу, схема ничем не отличается от решения предыдущих систем. Отличие только в том, что мы уравнения не складываем, а вычитаем. Мы проводим алгебраическое вычитание.
Другими словами, как только вы видите систему, состоящую из двух уравнений с двумя неизвестными, первое, на что вам необходимо посмотреть — это на коэффициенты. Если они где-либо одинаковые, уравнения вычитаются, а если они противоположные — применяется метод сложения. Всегда это делается для того, чтобы одна из них исчезла, и в итогом уравнении, которая осталась после вычитания, осталась бы только одна переменная.
Разумеется, это еще не все. Сейчас мы рассмотрим системы, в которых уравнения вообще несогласованны. Т.е. нет в них таких переменных, которые были бы либо одинаковые, либо противоположные. В этом случае для решения таких систем применяется дополнительный прием, а именно домножение каждого из уравнений на специальный коэффициент. Как найти его и как решать вообще такие системы, сейчас мы об этом и поговорим.
Решение задач методом домножения на коэффициент
Пример № 1
Пример № 2
\[\left\< \begin
Нюансы решения
Ключевое правило здесь следующее: всегда умножаем лишь на положительные числа — это избавит вас от глупых и обидных ошибок, связанных с изменением знаков. А вообще, схема решения довольно проста:
Решение задач с дробными числами
Пример № 1
Вычитаем уравнения друг из друга:
Пример № 2
\[\left\< \begin
Применяем метод вычитания:
Нюансы решения
Но как найти числа, на которые необходимо домножать уравнения? Ведь если домножать на дробные числа, мы получим новые дроби. Поэтому дроби необходимо домножить на число, которое бы дало новое целое число, а уже после этого домножать переменные на коэффициенты, следуя стандартному алгоритму.
Решение сложных систем уравнений
В качестве заключительного аккорда к сегодняшнему видеоуроку давайте рассмотрим пару действительно сложных систем. Их сложность будет состоять в том, что в них и слева, и справа будут стоять переменные. Поэтому для их решения нам придется применять предварительную обработку.
Система № 1
\[\left\< \begin
Каждое уравнение несет в себе определенную сложность. Поэтому с каждым выражением давайте поступим как с обычной линейной конструкцией.
\[3\left( 2x-y \right)+5=-2\left( x+3y \right)+4\]
\[6\left( y+1 \right)-1=5\left( 2x-1 \right)+8\]
Итого мы получим окончательную систему, которая равносильна исходной:
Система № 2
Преобразуем первое выражение:
\[4\left( a-3b \right)-2a=3\left( b+4 \right)-11\]
Разбираемся со вторым:
\[-3\left( b-2a \right)-12=2\left( a-5 \right)+b\]
Итого, наша первоначальная система примет такой вид:
Вычитаем из первой конструкции вторую:
Вот и все. Надеюсь, этот видеоурок поможет вам разобраться в этой нелегкой теме, а именно в решении систем простых линейных уравнений. Дальше еще будет много уроков, посвященных этой теме: мы разберем более сложные примеры, где переменных будет больше, а сами уравнения уже будут нелинейными. До новых встреч!
Линейные уравнения. Решение систем линейных уравнений. Способ сложения.
Метод сложения – решая системы линейных уравнений методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ, где в одном из уравнений есть лишь одна переменная.
Для решения системы способом почленного сложения (вычитания) следуйте следующим шагам:
1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.
2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.
3. Далее необходимо решить линейное уравнение, которое мы получили и найти решение системы.
Рассмотрим на примерах.
Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (–1 и 1). В таком случае уравнения легко сложить почленно:
Действия, которые обведены красным цветом, выполняем в уме.
Результатом почленного сложения стало исчезновение переменной y. Именно в этом и В этом, собственно, и заключается смысл метода – избавиться от 1-ой из переменных.
В виде системы решение выглядит где-то так:
Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:
Нужно подобрать число, которое можно поделить и на 3 и на 4, при этом нужно, что бы это число было минимально возможным. Это наименьшее общее кратное. Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: 
1-е уравнение умножаем на 
3-е уравнение умножаем на 
Далее из 1-го уравнения почленно вычитаем 2-е.
Обратите внимание, что можно делать и наоборот – из 2-го уравнения вычесть 1-е, разницы нет.
Далее подставляем, найденное значение в любое из уравнений системы, к примеру, в 1-е:
Ответ: 
Математика
Тестирование онлайн
Система линейных уравнений
Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой
При решении системы уравнений используют свойства, справедливые для решения уравнений.
Решение системы линейных уравнений способом подстановки
Рассмотрим пример
1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:
2) Подставляем во второе уравнение системы вместо y выражение 3х-7:
3) Решаем полученное второе уравнение:
4) Полученное решение подставляем в первое уравнение системы:
Решение системы линейных уравнений способом сложения
Решим систему уравнений из предыдущего примера 
1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».
2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.
3) Полученное решение подставляем в первое уравнение системы:
Решение системы линейных уравнений графическим способом
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Графическое решение системы
Метод введения новых переменных
Замена переменных может привести к решению более простой системы уравнений, чем исходная.
Рассмотрим решение системы
Введем замену 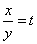
Переходим к первоначальным переменным
Особые случаи
Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.
Пусть дана система
1) Если 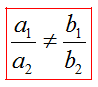
2) Если 
3) Если 
Метод Гаусса*
Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.
Системы уравнений
Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений с двумя неизвестными.
Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют « x » и « y »), которые объединены в общую систему фигурной скобкой.
Например, система уравнений может быть задана следующим образом.
| x + 5y = 7 |
| 3x − 2y = 4 |
Чтобы решить систему уравнений, нужно найти и « x », и « y ».
Как решить систему уравнений
Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.
Способ подстановки
или
«железобетонный» метод
Первый способ решения системы уравнений называют способом подстановки или «железобетонным».
Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений, всегда пробуйте решить её методом подстановки.
Разберем способ подстановки на примере.
| x + 5y = 7 |
| 3x − 2y = 4 |
Выразим из первого уравнения « x + 5y = 7 » неизвестное « x ».
Чтобы выразить неизвестное, нужно выполнить два условия:
Перенесём в первом уравнении « x + 5 y = 7 » всё что содержит « x » в левую часть, а остальное в правую часть по правилу переносу.
При « x » стоит коэффициент равный единице, поэтому дополнительно делить уравнение на число не требуется.
| x = 7 − 5y |
| 3x − 2y = 4 |
Теперь, вместо « x » подставим во второе уравнение полученное выражение
« x = 7 − 5y » из первого уравнения.
| x = 7 − 5y |
| 3(7 − 5y) − 2y = 4 |
Подставив вместо « x » выражение « (7 − 5y) » во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным « y ». Решим его по правилам решения линейных уравнений.
| x = 7 − 5y |
| 3(7 − 5y) − 2y = 4 (*) |
Мы нашли, что « y = 1 ». Вернемся к первому уравнению « x = 7 − 5y » и вместо « y » подставим в него полученное числовое значение. Таким образом можно найти « x ». Запишем в ответ оба полученных значения.
| x = 7 − 5y |
| y = 1 |
| x = 7 − 5 · 1 |
| y = 1 |
| x = 2 |
| y = 1 |
Ответ: x = 2; y = 1
Способ сложения
Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения. Вернемся к нашей системе уравнений еще раз.
| x + 5y = 7 |
| 3x − 2y = 4 |
По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные уравнения, получить такое уравнение, в котором останется только одно неизвестное.
Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.
При сложения уравнений системы левая часть первого уравнения полностью складывается с левой частью второго уравнения, а правая часть полностью складывается с правой частью.
| x + 5y = 7 | (x + 5y) + (3x − 2y) = 7 + 4 |
| + => | x + 5y + 3x − 2y = 11 |
| 3x − 2y = 4 | 4x + 3y = 11 |
При сложении уравнений мы получили уравнение « 4x + 3y = 11 ». По сути, сложение уравнений в исходном виде нам ничего не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.
Вернемся снова к исходной системе уравнений.
| x + 5y = 7 |
| 3x − 2y = 4 |
Чтобы при сложении неизвестное « x » взаимноуничтожилось, нужно сделать так, чтобы в первом уравнении при « x » стоял коэффициент « −3 ».
Для этого умножим первое уравнение на « −3 ».
При умножении уравнения на число, на это число умножается каждый член уравнения.
| x + 5y = 7 | ·(−3) |
| 3x − 2y = 4 |
| x · (−3) + 5y · (−3) = 7 · (−3) |
| 3x − 2y = 4 |
| −3x −15y = −21 |
| 3x − 2y = 4 |
Теперь сложим уравнения.
| −3x −15y = −21 | (−3x −15y ) + (3x − 2y) = −21 + 4 |
| + => | − 3x − 15y + 3x − 2y = −21 + 4 |
| 3x − 2y = 4 | −17y = −17 |:(−17) |
| y = 1 |
Мы нашли « y = 1 ». Вернемся к первому уравнению и подставим вместо « y » полученное числовое значение и найдем « x ».
| x = 7 − 5y |
| y = 1 |
| x = 7 − 5 · 1 |
| y = 1 |
| x = 2 |
| y = 1 |
Ответ: x = 2; y = 1
Пример решения системы уравнения
способом подстановки
Выразим из первого уравнения « x ».
| x = 17 + 3y |
| x − 2y = −13 |
Подставим вместо « x » во второе уравнение полученное выражение.
| x = 17 + 3y |
| (17 + 3y) − 2y = −13 (*) |
Подставим в первое уравнение полученное числовое значение « y = −30 » и найдем « x ».
| x = 17 + 3y |
| y = −30 |
| x = 17 + 3 · (−30) |
| y = −30 |
| x = 17 −90 |
| y = −30 |
| x = −73 |
| y = −30 |
Ответ: x = −73; y = −30
Пример решения системы уравнения
способом сложения
Рассмотрим систему уравнений.
| 3(x − y) + 5x = 2(3x − 2) |
| 4x − 2(x + y) = 4 − 3y |
Раскроем скобки и упростим выражения в обоих уравнениях.
| 3x − 3y + 5x = 6x − 4 |
| 4x − 2x − 2y = 4 − 3y |
| 8x − 3y = 6x − 4 |
| 2x −2y = 4 − 3y |
| 8x − 3y − 6x = −4 |
| 2x −2y + 3y = 4 |
| 2x − 3y = −4 |
| 2x + y = 4 |
Мы видим, что в обоих уравнениях есть « 2x ». Наша задача, чтобы при сложении уравнений « 2x » взаимноуничтожились и в полученном уравнении осталось только « y ».
Для этого достаточно умножить первое уравнение на « −1 ».
| 2x − 3y = −4 | ·(−1) |
| 2x + y = 4 |
| 2x · (−1) − 3y · (−1) = −4 · (−1) |
| 2x + y = 4 |
| −2x + 3y = 4 |
| 2x + y = 4 |
Теперь при сложении уравнений у нас останется только « y » в уравнении.
| −2x + 3y = 4 | (−2x + 3y ) + (2x + y) = 4 + 4 |
| + => | − 2x + 3y + 2x + y = 4 + 4 |
| 2x + y = 4 | 4y = 8 | :4 |
| y = 2 |
Подставим в первое уравнение полученное числовое значение « y = 2 » и найдем « x ».
6.9.3. Решение систем линейных уравнений методом сложения.
Чтобы решить систему линейных уравнений с двумя переменными методом сложения, надо:
1) умножить левую и правую части одного или обоих уравнений на некоторое число так, чтобы коэффициенты при одной из переменных в уравнениях стали противоположными числами;
2) сложить почленно полученные уравнения и найти значение одной из переменных;
3) подставить найденное значение одной переменной в одно из данных уравнений и найти значение второй переменной.
Если в данной системе коэффициенты при одной переменной являются противоположными числами, то решение системы начнём сразу с пункта 2).
Примеры. Решить систему линейных уравнений с двумя переменными методом сложения.
Так как коэффициенты при у являются противоположными числами (-1 и 1), то решение начинаем с пункта 2). Складываем уравнения почленно и получим уравнение 8х = 24. Вторым уравнением системы можно записать любое уравнение исходной системы.
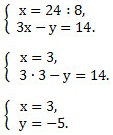
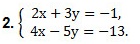
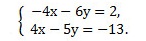
Мы получим равносильную систему уравнений, в которой 1-ое уравнение есть сумма двух уравнений прежней системы, а 2-м уравнением системы мы запишем 1-ое уравнение исходной системы (обычно записывают уравнение с меньшими коэффициентами):
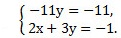
Ответ: (-2; 1).