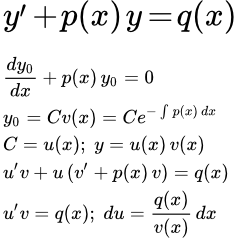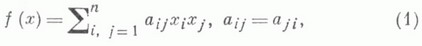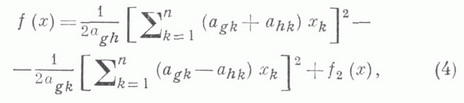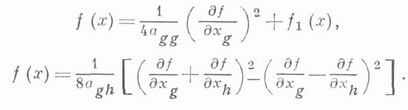в чем заключается метод лагранжа

Условная оптимизация. Метод множителей Лагранжа.

Условная оптимизация. Метод множителей Лагранжа.

Метод множителей Лагранжа (в англ. литературе «LaGrange’s method of undetermined multipliers») ˗ это численный метод решения оптимизационных задач, который позволяет определить «условный» экстремум целевой функции (минимальное или максимальное значение)

при наличии заданных ограничений на ее переменные в виде равенств (т.е. определена область допустимых значений)

˗ это значения аргумента функции (управляемые параметры) на вещественной области при котором значение функции стремится к экстремуму. Применение названия «условный» экстремум связано с тем, что на переменные наложено дополнительное условие, которое ограничивает область допустимых значений при поиске экстремума функции.

Метод множителей Лагранжа позволяет задачу поиска условного экстремума целевой функции на множестве допустимых значений преобразовать к задаче безусловной оптимизации функции.

В случае если функции и непрерывны вместе со своими частными производными, то существуют такие переменные λ не равные одновременно нулю, при которых выполняется следующее условие:

Таким образом, в соответствии с методом множителей Лагранжа для поиска экстремума целевой функции на множестве допустимых значений составляю функцию Лагранжа L(х, λ), которую в дальнейшем оптимизируют:

где λ ˗ вектор дополнительных переменных, называемых неопределенными множителями Лагранжа.

Таким образом, задача нахождения условного экстремума функции f(x) свелась к задаче поиска безусловного экстремума функции L(x, λ).

Далее в соответствии с методом определяют частные производные функции Лагранжа:

и

Необходимое условие экстремума функции Лагранжа задается системой уравнений (система состоит из «n + m» уравнений):

Решение данной системы уравнений позволяет определить аргументы функции (Х), при которых значение функции L(x, λ), а также значение целевой функции f(x) соответствуют экстремуму.

Величина множителей Лагранжа (λ) имеет практический интерес в случае, если ограничения представлены в форме со свободным членом уравнения (константой). В этом случае можно рассматривать дальнейшее (увеличение/уменьшение) значения целевой функции за счет изменения значения константы в системе уравнения . Таким образом, множитель Лагранжа характеризует скорость изменения максимума целевой функции при изменении ограничивающей константы.

Существует несколько способов определения характера экстремума полученной функции:

Первый способ: Пусть – координаты точки экстремума, а — соответствующее значение целевой функции. Берется точка , близкая к точке , и вычисляется значение целевой функции :

— Если , то в точке имеет место максимум.

— Если , то в точке имеет место минимум.

Если в заданной точке , то целевая функция f(x) имеет в данной точке условный минимум, если же , то целевая функция f(x) имеет в данной точке условный максимум.

Третий способ: Также характер экстремума функции можно выяснить рассмотрев гессиан функции Лагранжа. Матрица Гессе представляет собой симметричную квадратную матрицу вторых частных производных функции в точке , в которой элементы матрицы симметричны относительно главной диагонали.

Для определения типа экстремума (максимум или минимум функции) можно воспользоваться правилом Сильвестра:

1. Для того, чтобы второй дифференциал функции Лагранжа был знакоположителен необходимо, чтобы угловые миноры функции были положительными . При таких условиях функция в этой точке имеет минимум.

2. Для того, чтобы второй дифференциал функции Лагранжа был знакоотрицателен , необходимо, чтобы угловые миноры функции чередовались, причем первый элемент матрицы должен быть отрицательнsv . При таких условиях функция в этой точке имеет максимум.

Под угловым минором понимаем минор, расположенный в первых k строках и k столбцах исходной матрицы.

Основное практическое значение метода Лагранжа заключается в том, что он позволяет перейти от условной оптимизации к безусловной и, соответственно, расширить арсенал доступных методов решения задачи. Однако задача решения системы уравнений, к которой сводится данный метод, в общем случае не проще исходной задачи поиска экстремума. Такие методы называются непрямыми. Их применение объясняется необходимостью получить решение экстремальной задачи в аналитической форме (допустим, для тех или иных теоретических выкладок). При решении конкретных практических задач обычно используются прямые методы, основанные на итеративных процессах вычисления и сравнения значений оптимизируемых функций.

Методика расчета

1 шаг: Определяем функцию Лагранжа из заданной целевой функции и системы ограничений:

2 шаг: Определение аналитических соотношений (в символьном виде) для поиска безусловного экстремума функции L(x, λ).

3 шаг: Решаем полученную систему линейных или нелинейных уравнений, используя соответствующие методы решения.

4 шаг: Определяем характер экстремума (максимум или минимум целевой функции) по любому из представленных выше методов.

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

Источник

Метод Лагранжа (вариации постоянной). Линейные дифференциальные уравнения первого порядка.

Рассмотрим решение линейного дифференциального уравнения первого порядка методом Лагранжа.

Метод вариации постоянной (Лагранжа)

В методе вариации постоянной мы решаем уравнение в два этапа. На первом этапе мы упрощаем исходное уравнение и решаем однородное уравнение. На втором этапе мы заменим постоянную интегрирования, полученную на первой стадии решения, на функцию. После чего ищем общее решение исходного уравнения.

Шаг 1 Решение однородного уравнения

Шаг 2 Заменим постоянную C на функцию

Теперь заменим постоянную C на функцию от x :
C → u ( x )
То есть, будем искать решение исходного уравнения (1) в виде:
(2)
Находим производную.

По правилу дифференцирования сложной функции:
.
По правилу дифференцирования произведения:

.
Подставляем в исходное уравнение (1):
(1) ;

.
Два члена сокращаются:
;
.
Интегрируем:
.
Подставляем в (2):
.
В результате получаем общее решение линейного дифференциального уравнения первого порядка:
.

Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа

Решаем однородное уравнение:

Разделяем переменные:

Умножим на :

Интегрируем:

Интегралы табличные:

Потенцируем:

Заменим постоянную e C на C и убираем знаки модуля:

Отсюда:

Заменим постоянную C на функцию от x :
C → u ( x )

Находим производную:
.
Подставляем в исходное уравнение:
;
;
Или:
;
.
Интегрируем:
;
Решение уравнения:
.

Общее решение уравнения:
.

Источник

ЛАГРАНЖА МЕТОД

— метод приведения квадратичной формы к сумме квадратов, указанный в 1759 Ж. Лагранжем (J. Lagrange). Пусть дана квадратичная форма

от ппеременных х 0 , x 1 . х п . с коэффициентами из поля k характеристики 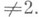Требуется привести эту форму к канонич. виду

при помощи невырожденного линейного преобразования переменных. Л. м. состоит в следующем. Можно считать, что не все коэффициенты формы (1) равны нулю. Поэтому возможны два случая.

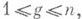
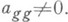
1) При некотором g,диагональный коэффициент Тогда

Лит.:[1] Г а н т м а х е р Ф. Р., Теория матриц, 2 изд., М., 1966; [2] К у р о ш А. Г., Курс высшей алгебры, 11 изд., М., 1975; [3] Александров П. С., Лекции по аналитической геометрии. М., 1968. И. В. Проскуряков.

Полезное

Смотреть что такое «ЛАГРАНЖА МЕТОД» в других словарях:

Лагранжа метод — Лагранжа метод [Lagrangian method] — метод решения ряда классов задач математического программирования с помощью нахождения седловой точки (x*, λ*) функции Лагранжа., что достигается приравниванием нулю частных производных этой функции по… … Экономико-математический словарь

Лагранжа метод множителей — метод решения задач на Условный экстремум; Л. м. м. заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции т. н. функции Лагранжа. Для задачи об экстремуме функции f (х1, x2. xn) при… … Большая советская энциклопедия

Метод Лагранжа (дифференциальные уравнения) — У этого термина существуют и другие значения, см. Метод Лагранжа. Метод Лагранжа (метод вариации произвольных постоянных) метод для получения общего решения неоднородного уравнения, зная общее решение однородного уравнения без нахождения… … Википедия

Метод Лагранжа приведения квадратичной формы к каноническому виду — У этого термина существуют и другие значения, см. Метод Лагранжа. Метод Лагранжа метод приведения квадратичной формы к каноническому виду, указанный в 1759 году Лагранжем. Описание Данный метод состоит в последовательном выделении в квадратичной… … Википедия

Источник

Алгоритм метода множителей Лагранжа

Метод множителей Лагранжа.

Метод множителей Лагранжа является одним из методов, которые позволяют решать задачи нелинейного программирования.

Нелинейное программирование-это раздел математического программирования, изучающий методы решения экстремальных задач с нелинейной целевой функцией и областью допустимых решений, определенной нелинейными ограничениями. В экономике это соответствует тому, что результаты (эффективность) возрастают или убывают непропорционально изменению масштабов использования ресурсов (или, что то же самое, масштабов производства): напр., из-за деления издержек производства на предприятиях на переменные и условно-постоянные; из-за насыщения спроса на товары, когда каждую следующую единицу продать труднее, чем предыдущую и т. д.

Задача нелинейного программирования ставится как задача нахождения оптимума определенной целевой функции

при выполнении условий

где x —вектор искомых переменных;

g (x) — функция ограничений (непрерывно дифференцируемая);

b — вектор констант ограничений.

Решение задачи нелинейного программирования (глобальный максимум или минимум) может принадлежать либо границе, либо внутренней части допустимого множества.

В отличие от задачи линейного программирования, в задаче программирования нелинейного оптимум не обязательно лежит на границе области, определенной ограничениями. Иначе говоря, задача состоит в выборе таких неотрицательных значений переменных, подчиненных системе ограничений в форме неравенств, при которых достигается максимум (или минимум) данной функции. При этом не оговариваются формы ни целевой функции, ни неравенств. Могут быть разные случаи: целевая функция нелинейная, а ограничения линейны; целевая функция линейна, а ограничения (хотя бы одно из них) нелинейные; и целевая функция, и ограничения нелинейные.

Задача нелинейного программирования встречается в естественных науках, технике, экономике, математике, в сфере деловых отношений и в науке управления государством.

Нелинейное программирование, например, связано с основной экономической задачей. Так в задаче о распределении ограниченных ресурсов максимизируют либо эффективность, либо, если изучается потребитель, потребление при наличии ограничений, которые выражают условия недостатка ресурсов. В такой общей постановке математическая формулировка задачи может оказаться невозможной, но в конкретных применениях количественный вид всех функций может быть определен непосредственно. Например, промышленное предприятие производит изделия из пластмассы. Эффективность производства здесь оценивается прибылью, а ограничения интерпретируются как наличная рабочая сила, производственные площади, производительность оборудования и т.д.

Результаты решения задачи нелинейного программирования являются подспорьем при принятии государственных решений. Полученное решение является, естественно, рекомендуемым, поэтому необходимо исследовать предположения и точность постановки задачи нелинейного программирования, прежде чем принять окончательное решение.

Нелинейные задачи сложны, часто их упрощают тем, что приводят к линейным. Для этого условно принимают, что на том или ином участке целевая функция возрастает или убывает пропорционально изменению независимых переменных. Такой подход называется методом кусочно-линейных приближений, он применим, однако, лишь к некоторым видам нелинейных задач.

Нелинейные задачи в определенных условиях решаются с помощью функции Лагранжа: найдя ее седловую точку, тем самым находят и решение задачи. Среди вычислительных алгоритмов Н. п. большое место занимают градиентные методы. Универсального же метода для нелинейных задач нет и, по-видимому, может не быть, поскольку они чрезвычайно разнообразны. Особенно трудно решаются многоэкстремальные задачи.

Одним из методов, которые позволяют свести задачу нелинейного программирования к решению системы уравнений, является метод неопределенных множителей Лагранжа.

С помощью метода множителей Лагранжа по существу устанавливаются необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничениями в виде ра­венств. При этом задача с ограничениями преобразуется в эквива­лентную задачу безусловной оптимизации, в которой фигурируют некоторые неизвестные параметры, называемые множителями Ла­гранжа.

Метод множителей Лагранжа заключается в сведении задач на условный экстремум к задачам на безусловный экстремум вспомогательной функции — т. н. функции Лагранжа.

Рассмотрим задачу минимизации функции n переменных с учетом одного ограничения в виде равенства:

В соответствии с методом множителей Лагранжа эта задача преобразуется в следующую задачу безусловной оптимизации:

минимизировать L(x,λ)=f(x)-λ*h(x) (3)

где Функция L(х;λ) называется функцией Лагранжа,

λ — неизвестная постоянная, которая носит название множителя Лагранжа. На знак λ никаких требований не накладывается.

Пусть при заданном значении λ=λ₀ безусловный минимум функции L(x,λ) по х достигается в точке x=x₀ и x₀ удовлетворяет уравнению h₁(x₀)=0. Тогда, как нетрудно видеть, x₀ минимизирует (1) с учетом (2), поскольку для всех значений х, удовлетворяющих (2), h₁(x)=0 и L(x,λ)=min f(x).

Разумеется, необходимо подобрать значение λ=λ₀ таким образом, чтобы координата точки безусловного минимума х₀ удовлетворяла равенству (2). Это можно сделать, если, рассматривая λ как переменную, найти безусловный минимум функции (3) в виде функции λ, а затем выбрать значение λ, при котором выполняется равенство (2). Проиллюстрируем это на конкретном примере.

Соответствующая задача безусловной оптимизации записывается в следующем виде:

Решение. Приравняв две компоненты градиента L к нулю, получим

→ x₁ 0 =λ

→ x₂ 0 =λ/2

Для того чтобы проверить, соответствует ли стационарная точка х° минимуму, вычислим элементы матрицы Гессе функции L(х;u), рассматриваемой как функция х,

H_L(x)= ,

которая оказывается положительно определенной.

Это означает, что L(х,u) — выпуклая функция х. Следовательно, координаты x₁ 0 =λ, x₂ 0 =λ/2 определяют точку глобального минимума. Оптимальное значение λ находится путем подстановки значений x₁ 0 и x₂ 0 в уравнение2x₁+x₂=2, откуда 2λ+λ/2=2 или λ 0 =4/5. Таким образом, условный минимум достигается при x₁ 0 =4/5 и x₂ 0 =2/5 и равен min f(x)=4/5.

При решении задачи из примера мы рассматривали L(х;λ) как функцию двух переменных x₁и x₂и, кроме того, предполагали, что значение параметра λ выбрано так, чтобы выполнялось ограни­чение. Если же решение системы

, j=1,2,3,…,n

в виде явных функций λ получить нельзя, то значения х и λ находятся путем решения следующей системы, состоящей из n+1 уравнений с n+1 неизвестными:

, j=1,2,3,…,n., h₁(x)=0

Для нахождения всех возможных решений данной системы можно использовать численные методы поиска (например, метод Ньютона). Для каждого из решений ( ) следует вычислить элементы матрицы Гессе функции L, рассматриваемой как функция х, и выяснить, является ли эта матрица положительно определенной (локальный минимум) или отрицательно определенной (локальный максимум).

Метод множителей Лагранжа можно распространить на случай, когда задача имеет несколько ограничений в виде равенств. Рассмотрим общую задачу, в которой требуется

Функция Лагранжа принимает следующий вид:

L(x,λ)=f(x)-

Если найти решение приведенной выше системы в виде функций вектора λ оказывается затруднительным, то можно расширить систему путем включения в нее ограничений в виде равенств

Решение расширенной системы, состоящей из n+К уравнений с n+К неизвестными, определяет стационарную точку функции L. Затем реализуется процедура проверки на минимум или максимум, которая проводится на основе вычисления элементов матрицы Гессе функции L, рассматриваемой как функция х, подобно тому, как это было проделано в случае задачи с одним ограничением. Для некоторых задач расширенная система n+К уравнений с n+K неизвестными может не иметь решений, и метод множителей Лагранжа оказывается неприменимым. Следует, однако, отметить, что такие задачи на практике встречаются достаточно редко.

Рассмотрим частный случай общей задачи нелинейного программирования, предполагая, что система ограничений содержит только уравнения, отсутствуют условия неотрицательности переменных и и — функции непрерывные вместе со своими частными производными

® max (min) (4)

(5)

Данную задачу называют задачей на условный экстремум или классической задачей оптимизации.

Чтобы найти решение этой задачи, вводят набор переменных называемых множителями Лагранжа, составляют функцию Лагранжа

(6)

находят частные производные и рассматривают систему n+m уравнений

(7)

с n+m неизвестными Всякое решение системы уравнений (7) определяет точку в которой может иметь место экстремум функции . Следовательно решив систему уравнений (7), получают все точки, в которых функция (6) может иметь экстремальные значения.

Алгоритм метода множителей Лагранжа

1.Составляем функцию Лагранжа.

2.Находим частные производные от функции Лагранжа по переменным x_J,λ_i и приравниваем их нулю.

3.Решаем систему уравнений (7), находим точки, в которых целевая функция задачи может иметь экстремум.

4.Среди точек, подозрительных на экстремум, находим такие, в которых достигается экстремум, и вычисляем значения функции (6) в этих точках.

Исходные данные:По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве x₁ изделий 1 способом затраты равны 4x₁+x₁ 2 руб., а при изготовлении x₂ изделий 2 способом они составляют 8x₂+x₂ 2 руб. Определить сколько изделий каждым из способов следует изготовить, чтобы затраты на производство продукции были минимальными.

Целевая функция для поставленной задачи имеет вид
®min при условиях x₁+x₂=180, x₂≥0.
1.Составляем функцию Лагранжа
.
2. Вычисляем частные производные по x₁, x_2, λ и приравниваем их нулю:

3. Решая полученную систему уравнений, находим x₁=91,x₂=89

Ответ: Количество изделий изготовленных первым способом равно х₁=91, вторым способом х₂=89 при этом значение целевой функции равно 17278 руб.

Источник