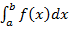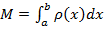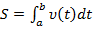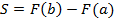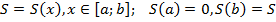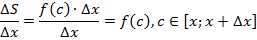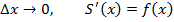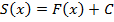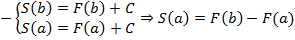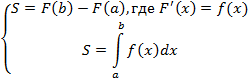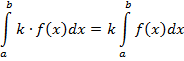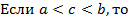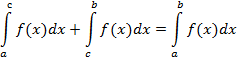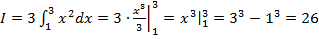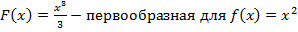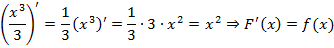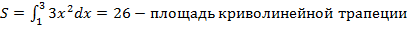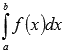в чем заключается геометрический смысл определенного интеграла
Лекция 1. Определение, геометрический смысл и свойства определенного интеграла



1.1. Определенный интеграл как предел интегральных сумм
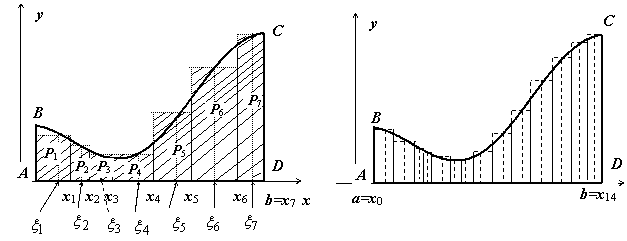
Пусть дана функция y = f(x) на отрезке [a, b], причем f / (x) ≥ 0 для любого 
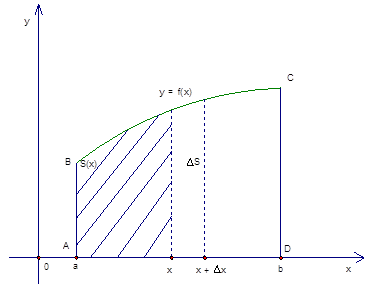
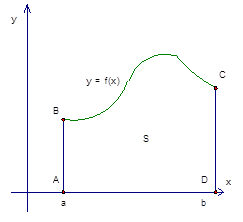
Задача. Найти площадь фигуры ABCD (криволинейная трапеция)



Тогда приближенно площадь каждого прямоугольника:
Просуммировав площади всех прямоугольников, получим приближенное значение площади искомой фигуры:

Величина Δ x – шаг разбиения. При уменьшении шага разбиения Δ x → 0, т.е. количество разбиений n → ∞. При этом формула (1) станет более точной. Тогда точное значение площади – предел (если он существует).
(2) 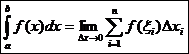
Значения a и b – соответственно нижний и верхний пределы интегрирования. Таким образом, определенный интеграл представляет собой число, а не формулу в отличие от неопределенного интеграла.
В виде формулы (2) определение впервые сформулировано немецким математиком Бернардом Риманом. Поэтому интегральную сумму часто называют римановской суммой, а интеграл – интегралом Римана. Знак ∫ введен Лейбницем, это удлиненная первая буква от латинского слова « summa».
1.2. Геометрический смысл определенного интеграла



В этом заключается геометрический смысл определенного интеграла. При этом:
1.3. Свойства определенного интеграла
1) Постоянный множитель можно выносить за знак интеграла: 
2) О.И. от алгебраической суммы двух непрерывных функций равен алгебраической сумме их интегралов: 
3) Если 



6) Если f(x) ≥ g(x) для любого x из [a, b], то
Площадь фигуры, заключенной между графиками:
(Из функции, график которой лежит выше, вычитается функция, график которой лежит ниже);
7) Теорема о среднем. Если функция f(x) непрерывна на [a, b], то существует такая точка с из [a, b], что: 
1.7. Геометрический смысл определённого интеграла
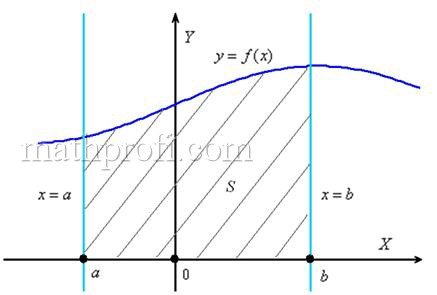
Начнем с криволинейной трапеции. Криволинейной трапецией называется плоская фигура, ограниченная осью 




И смысл прост. Определённый интеграл 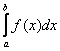

В самом начале курса я говорил, что определенный интеграл – это число. А сейчас пришла пора констатировать еще один полезный факт. С точки зрения геометрии, это число – есть ПЛОЩАДЬ.
Рассмотрим, например, определенный интеграл 


И вообще, любому определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры. Эта фигура не обязательно расположена выше оси абсцисс, она может располагаться и ниже, может располагаться и там и там; может быть более простой или более сложной.
В простых случаях (квадрат, треугольник и т.д.) площадь легко рассчитывается по «школьным» формулам, но что делать в случаях остальных? Привлечь на помощь определённый интеграл! Рассмотрим самую популярную и самую распространенную тематическую задачу:
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Суть геометрического смысла определенного интеграла
Понятие определенного интеграла
Определенным интегралом от функции y = f (x) относительно отрезка [a;b] называют предел интегральных сумм Sn при n, стремящемся к бесконечности.
В данном выражении:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В чем заключается геометрический смысл определенного интеграла
Геометрический смысл определенного интеграла можно записать таким образом:
К примеру, масса неоднородного стержня AD будет представлена с помощью равенства:
Скорость перемещения точки вдоль прямой составит:
Вычисление определенного интеграла и площади криволинейной трапеции основано на теореме.
Теорема о вычислении определенного интеграла
В том случае, когда f является непрерывной и неотрицательной функцией на отрезке [a;b], а F представляет собой ее первообразную на этом интервале, площадь соответствующей криволинейной трапеции будет определяться как приращение первообразной на интервале [a;b].
Теорему можно записать в таком виде:
Полученное выражение можно представить с помощью графика:
Доказательство теоремы
Доказать утверждение можно путем последовательных действий. Сначала требуется на интервале [a;b] зафиксировать х и найти площадь фигуры, которая расположены под кривой на отрезке [a;х]. Таким образом, каждому х соответствует S(х), и получится новая функция:
Таким образом, площадь криволинейной трапеции будет определяться, как приращение любой первообразной на интервале [a;b].
Формула Ньютона-Лейбница
Функция y = f (x) является непрерывной в интервале [a;b]. Непрерывную функцию можно представить на графике:
Свойства определенного интеграла
Определенный интеграл обладает рядом характерных свойств:
Как найти площадь криволинейной трапеции при помощи интеграла
В качестве примера можно рассмотреть определенный интеграл:
С помощью геометрической интерпретации можно определить площадь криволинейной трапеции:
Графически функцию и площадь трапеции можно изобразить, таким образом:
Геометрический смысл определенного интеграла
Геометрия способна помочь решать различные задачи, в том числе относительно вычисления площади, то, что является неотъемлемой частью теории площади. Достаточно легко и просто рассчитать площадь, когда она является легко распознаваемой и с виду представляет собой какую-ту известную геометрическую фигуру правильной формы. Совсем другое, когда речь о вычислении площади неправильных фигур и тогда на помощь можно позвать другие хитрости геометрии, в том числе использовать геометрический смысл определенного интеграла.
Интегральное вычисление позволяет рассчитать в точности площадь сложных фигур и это достаточно просто, если понять что собой представляет геометрический смысл определенного интеграла. Данные расчеты можно рассмотреть наглядно на примере криволинейной трапеции. Связь между интегралом и параметром площадь фигуры определенно существует, остается только научиться распознавать ее и использовать для расчета площади.
Для начала следует понять, что такое криволинейная трапеция, ведь именно от ее площади нужно отталкиваться при вычислении. Криволинейная трапеция это нечто иное как плоская фигура, чьи границы определяются функцией непрерывного неотрицательного типа и двумя прямыми и осью абсцисс. Согласно этому понятию можно суммировать значения функции y = f(x) и таким образом определить площадь фигуры. Значения, которые необходимо суммировать, важно учитывать через бесконечно малые промежутки по оси между точками а и b, которые определяют границы фигуры. Такой подход к расчету площади позволяет разбивать целую фигуру на бесконечное количество прямоугольников, что упрощает расчет всей площади. У каждого прямоугольника есть длина и ширина согласно значению ординаты f(x) и оси Ох через бесконечно малые промежутки.
Формула расчета площади криволинейной трапеции
Геометрический смысл определенного интеграла определение
Геометрический смысл определенного интеграла в ином понимании это площадь криволинейной трапеции для неотрицательной и непрерывной функции, которая расположена между двумя интервалами. Так как криволинейную трапеции можно воспринимать как квадрируемую фигуру, то и подобный тип расчета площади является актуальным. Для того чтобы определенный интеграл мог существовать, очень важно, чтобы соблюдалось условие непрерывности функции.
Существует возможность определить, если заданная функция имеет определенный интеграл, но согласно общепринятой теореме в первую очередь рассматривается интегрируемость непрерывных функций. Изучение геометрического смысла определенного интеграла, как правило, всегда изучается в сочетание с определением площади для фигуры под названием криволинейная трапеция. Практическая польза данного понятия сводится к возможности расчета площади сложных фигур. Данные правила расчета актуальны для фигур с площадью в рамках линий x=g(y) и y=f(x).
Все очень просто, достаточно вычислить интеграл и площадь сложной фигуры станет известной. Любую фигуру созданную из несколько линий по типу y = f(x), x = a, y = 0, x = b может вычисляться таким образом. Расчет возможен при условии, что функция не является положительной на отрезке между а и b, только принцип расчета частично отличается.
Обобщая вышесказанное можно заявить, что каждая сложная фигура является по факту криволинейной трапецией, а это значит, все вышеперечисленные расчеты актуальны для них. Успешный расчет площади сложных фигур возможен, если начинать с расчета более простых примеров и постепенно совершенствовать свои навыки. Согласно всему вышесказанному становится понятно, что геометрический смысл определенного интеграла позволяет решать одну из сложных задач геометрии – вычисление площади сложных фигур. Это становится возможным за счет применения интеграла, то, что одновременно и упрощает и усложняет задачу. В мире математики все понятия между собой тесно связаны и поэтому в обучении не должно быть пробелов, если вы стремитесь к определенным успехам.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Геометрический смысл определенного интеграла
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Пусть непрерывная функция y = f(x) задана на некотором отрезке [ a ; b ].
2) Внутри каждого из частичных отрезков произвольно выберем точку c i [ x i –1 ; x i ] и вычислим значения функции в этих точках (вычислим f(c i ) ).
3) S n = f(c 1 ) ( x 1 – x 0 ) + f(c 2 ) ( x 2 – x 1 ) + … + f(c n ) ( x n – x n –1 )
Sn – интегральная сумма.
4) = max x i – наибольший по длине частичный отрезок (диаметр разбиения).
ОПРЕДЕЛЕНИЕ: Если существует конечный предел интегральных сумм, который не зависит ни от разбиения отрезка [ a ; b ], ни от выбора точек частичных отрезков, то этот предел называется определенным интегралом.


Отображаем симметрично оси OX

СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА:
1)
2)
3)
4)
5)
6) Если f(x) (x) для всех x [ a ; b ], то
7) Если M – наибольшее значение функции f(x) на отрезке [ a ; b ], а m – наименьшее значение функции f(x) на отрезке [ a ; b ], то
Доказывается на основании 6, 4 и 3 свойств.
8) Теорема о среднем (значении):
Для любой непрерывной на [ a ; b ] функции f(x) существует точка c [ a ; b ] такая, что
f(c) – среднее значение функции на отрезке [ a ; b ].
10) a) Интеграл от нечетной функции по симметричному отрезку равен нулю
б) Интеграл от четной функции по симметричному отрезку равен удвоенному интегралу по половине отрезка


б)
Рассмотрим интеграл 

Доказываем непосредственно. Распишем производную Ф( x ) по определению.
Распишем по 8 свойству:
Чтобы продифференцировать интеграл по верхнему пределу нужно в подынтегральную функцию подставить верхний предел.
ТЕОРЕМА: Если F(x) – первообразная f(x) на отрезке [ a ; b ], то
Найти среднее значение функции y = – x 2 + 5 x – 6 на отрезке [1; 5].
ТЕОРЕМА: Пусть задан интеграл 
2) ( t ), (t) непрерывны на [a; b];
3) f( (t)) определена на [a; b], то