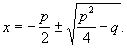в чем суть алгебры

Алгебра

А́лгебра (от араб. الجبر ‎‎, «аль-джабр» — восполнение [1] ) — раздел математики, который можно грубо охарактеризовать как обобщение и расширение арифметики. Слово «алгебра» также употребляется в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающий обычные операции сложения и умножения чисел.

Алгебра — это наука, изучающая алгебраические системы с точностью до изоморфизма.

Алгебраическая система — упорядоченная пара множеств . Первое множество () — элементы какой либо природы (числа, понятия, буквы). Второе множество () — операции над первым множеством (сложение, умножение, возведение в степень). Примеры: группа, кольцо, поле.

Содержание

История

Истоки алгебры уходят к временам глубокой древности. Ещё 4000 лет назад вавилонские учёные могли решать квадратные уравнения. Тогда никаких обозначений не было, и уравнения записывались в словесной форме. Первые обозначения появились в Древней Греции благодаря учёному Диофанту. Неизвестное число он назвал «ἀριθμός», вторую степень неизвестного — «δύναμις», третью «κύβος», четвёртую — «дюнамодюнамис», пятую — «дюнамокюбос», шестую — «кюбоккюбос». Все эти величины он обозначал сокращениями (ар, дю, кю, ддю, дкю, ккю). Ни вавилоняне, ни греки не знали и не признавали отрицательные числа.

За 2000 лет до нашего времени китайские учёные решали уравнения первой степени и их системы, а также квадратные уравнения. Они уже знали отрицательные и иррациональные числа. Поскольку в китайском языке каждый символ обозначает понятие, то сокращений не было. В 13 веке китайцы открыли закон образования биномиальных коэффициентов, ныне известный как «треугольник Паскаля». В Европе он был открыт лишь 250 лет спустя. [2]

В 12 веке алгебра попала в Европу. С этого времени начинается её бурное развитие. Были открыты способы решения уравнений 3 и 4 степеней. Распространения получили отрицательные и комплексные числа. Было доказано, что любое уравнение выше 4 степени нельзя решить алгебраическим способом.

Вплоть до второй половины XX века практическое применение алгебры ограничивалось, в основном, решением алгебраических уравнений и систем уравнений с несколькими переменными. Во второй половине XX века началось бурное развитие ряда новых отраслей техники. Появились электронно-вычислительные машины, устройства для хранения, переработки и передачи информации, системы наблюдения типа радара. Проектирование новых видов техники и их использование немыслимо без применения современной алгебры. Так, электронно-вычислительные машины устроены по принципу конечных автоматов. Для проектирования электронно-вычислительных машин и электронных схем используются методы булевой алгебры. Современные языки программирования для ЭВМ основаны на принципах теории алгоритмов. Теория множеств используется в системах компьютерного поиска и хранения информации. Теория категорий используется в задачах распознавания образов, определении семантики языков программирования, и других практических задачах. Кодирование и декодирование информации производится методами теории групп. Теория рекуррентных последовательностей используется в работе радаров. Экономические расчеты невозможны без использования теории графов. Математическое моделирование широко использует все разделы алгебры.

Классификация

Алгебру можно грубо разделить на следующие категории:

В некоторых напралениях углублённого изучения, аксиоматические алгебраические системы, такие как группы, кольца, поля и алгебры над полем на присутствие геометрических структур (метрик и топологий), совместимых с алгебраическими структурами. Список некоторых разделов функционального анализа:

Элементарная алгебра

Элементарная алгебра — раздел алгебры, который изучает самые базовые понятия. Обычно изучается после изучения основных понятий арифметики. В арифметике изучаются числа и простейшие (+, −, ×, ÷) действия с ними. В алгебре числа заменяются на переменные (a,b,c,x,y и так далее). Такой подход полезен, потому что:

Источник

А́ЛГЕБРА

Том 1. Москва, 2005, стр. 415

Скопировать библиографическую ссылку:

А́ЛГЕБРА [ср.-век. лат. al­geb­ra, от араб. аль-джебр, аль-джабр – вос­со­е­ди­не­ние (от­дель­ных ча­стей урав­не­ния)], раз­дел ма­те­ма­ти­ки, при­над­ле­жа­щий, на­ря­ду с ариф­ме­ти­кой и гео­мет­ри­ей, к чис­лу ста­рей­ших вет­вей этой нау­ки; она изу­ча­ет опе­ра­ции над ма­те­ма­тич. объ­ек­та­ми и влия­ет на фор­ми­ро­ва­ние об­щих по­нятий и ме­то­дов ма­те­ма­ти­ки. За­да­чи и ме­то­ды А. за­клю­ча­лись пер­во­на­чаль­но в со­став­ле­нии и ре­ше­нии урав­не­ний. В свя­зи с ис­сле­до­ва­ния­ми урав­не­ний раз­ви­ва­лось по­ня­тие чис­ла, бы­ли вве­де­ны от­ри­ца­тель­ные, ра­ци­о­наль­ные, ир­ра­цио­наль­ные и ком­плекс­ные чис­ла; об­щее ис­сле­до­ва­ние свойств этих чи­сло­вых сис­тем от­но­сит­ся к А. В ал­геб­ре сфор­ми­ро­ва­лись бу­к­вен­ные обо­зна­че­ния, по­зво­лив­шие за­пи­сать свой­ст­ва дей­ст­вий над чис­ла­ми в фор­ме, не со­дер­жа­щей кон­крет­ных чи­сел. Пре­об­ра­зо­ва­ния по оп­ре­де­лён­ным пра­ви­лам (свя­зан­ным со свой­ст­ва­ми дей­ст­вий) бу­к­вен­ных вы­ра­же­ний со­став­ля­ет ап­па­рат клас­сич. А. Раз­ви­тие А. ока­за­ло боль­шое влия­ние на раз­ви­тие но­вых об­лас­тей ма­те­ма­ти­ки, в ча­ст­но­сти ма­те­ма­тич. ана­ли­за, диф­фе­рен­ци­аль­но­го и ин­те­граль­но­го ис­чис­ле­ния. При­ме­не­ние А. воз­мож­но всю­ду, где при­хо­дит­ся иметь де­ло с опе­ра­ция­ми, ана­ло­гич­ны­ми сло­же­нию и ум­но­же­нию чи­сел. Эти опе­ра­ции мо­гут про­из­во­дить­ся над объ­ек­та­ми са­мой раз­лич­ной при­ро­ды. Наи­бо­лее из­вест­ным при­ме­ром та­ко­го рас­ши­рен­но­го при­ме­не­ния ал­геб­ра­ич. ме­то­дов яв­ля­ет­ся век­тор­ная ал­геб­ра (см. Ли­ней­ная ал­геб­ра ) и её даль­ней­шее обоб­ще­ние – тен­зор­ная ал­геб­ра (см. Тен­зор­ное ис­чис­ле­ние ), став­шая од­ним из важ­ных средств совр. фи­зи­ки.

Источник

Классификация раздела

Алгебра является разделом математики. Она классифицируется на несколько видов:

Каждый из этих разделов решает определенные задачи. При этом наука не стоит на месте и продолжает развитие.

Древняя история

Информация об истории возникновения алгебры связывается с древними рукописями. В те времена появилось понятие о натуральных числах, с которыми можно было проводить арифметические операции. Такая потребность возникла в связи с проведением астрономических и других видов расчетов. Изучая историю алгебры, становится понятно, что ее зарождение произошло в античной Греции.

Происхождение науки связывается с мыслителем Диофантом. На сегодняшний день трудно сказать, кто придумал алгебру, но именно этим человеком были впервые введены буквенные обозначения чисел. На основании полученных сообщений известно, что Диофант знал о сокращении чисел и умел переносить члены из разных частей уравнения.

Информация об ученом содержится только в одном историческом труде, поэтому сказать точно, что математик создал алгебру, невозможно. К тому же этот источник дошел до нынешних времен не в полном объеме.

Продвижение на Восток

Достижения европейцев в области развития алгебры прервались после нашествий варварских племен. Кроме того, уменьшение к ней интереса произошло с открытием геометрии, которая стала считаться основным разделом математики. В этот период многие науки получили свое развитие на Востоке. Здесь продолжилось становление и алгебры. Поскольку все достижения Европы практически были забыты, создателем этой науки в мусульманском мире считается Ала-Хорезми. Произошло это после создания им трактата под названием «Учение об отношениях, перестановках и решениях». Некоторые ученые считают, что слово «алгебра» может вести свое начало от термина «алгоритм».

При этом существуют гипотезы, что мусульманский мир опирался в своих изучениях на европейские достижения. В некоторых их летописях присутствуют фамилии греческих последователей Диофанта, приводятся их высказывания относительно этой науки.

Вклад других стран

Основателем алгебры считается Ала-Хорезми, но особого развития она у арабов она получила. Однако именно они изобрели на своем языке арабские цифры, которые применяются в современном мире. Существенный вклад в развитие науки внесли представители и других стран. Кратко их достижения выражаются в следующем:

Таким образом, в развитии этого раздела принимали участие многие страны мира. Их исследовательские работы вносили общий вклад в становление алгебры.

Под конец XVI века эта часть математики снова возвращается в Европу, откуда она взяла свое начало. Этому способствовало купечество, разъезжающее по всему свету и знакомившееся с математикой. Дальнейший толчок произошел после распада феодальной системы. Страны, ставшие на капиталистический путь развития, уже не могли обойтись без алгебраических действий.

Алгебра относится к наиболее интересным наукам, которые изучаются учениками школ и студентами вузов. Учащиеся постоянно пишут рефераты и готовят доклады на различные темы, относящиеся к этому разделу математики. В дальнейшем они зачитывают свои работы на уроках.

Источник

Алгебра

Полезное

Смотреть что такое «Алгебра» в других словарях:

алгебра — алгебра, ы … Русский орфографический словарь

*-алгебра — (алгебра с инволюцией, алгебра с операцией сопряжения) ассоциативная алгебра с инволюцией, которая имеет свойства подобные комплексному сопряжению. Содержание 1 * кольцо 2 * алгебра 3 C* алгебра … Википедия

АЛГЕБРА — (араб. al djebr восстановление разрозненных частей). Часть математики, рассматривающая общие величины, обозначая их буквами и знаками. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АЛГЕБРА араб. al djebr,… … Словарь иностранных слов русского языка

Алгебра А — Базисом предложенной Крисом Дейтом и Хью Дарвеном Алгебры A являются операции реляционного отрицания (дополнения), реляционной конъюнкции (или дизъюнкции) и проекции (удаления атрибута). Реляционные аналоги логических операций определяются в… … Википедия

АЛГЕБРА — АЛГЕБРА, область МАТЕМАТИКИ, посвященная изучению уравнений, содержащих цифры и буквенные обозначения, которые представляют величины, подлежащие определению. Например, у+х=8 это алгебраическое уравнение, содержащее переменные х и у. Если значение … Научно-технический энциклопедический словарь

АЛГЕБРА — АЛГЕБРА, часть математики, развившаяся в связи с задачей о решении алгебраических уравнений. Слово алгебра арабское (аль джебр), означает один из приемов преобразования алгебраических уравнений. Решение уравнений 1 й и 2 й степеней известно еще с … Современная энциклопедия

Алгебра — вместе с арифметикой есть наука о числах и через посредство чисел о величинах вообще. Не занимаясь изучением свойств каких нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин как таковых, независимо от… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

алгебра — ы ж. algèbre f., нем. Algebra <ср. лат. algebra. 1380. Лексис. мат. Алгебра же назвася от изобретателя гебер нарицаемаго. Арифм. Магн. 226. Имя самое алгебры есть арапское, которые ее назыают Алжабр Валмукабала, то есть наверстать или… … Исторический словарь галлицизмов русского языка

Алгебра — АЛГЕБРА, часть математики, развившаяся в связи с задачей о решении алгебраических уравнений. Слово “алгебра” арабское (аль джебр), означает один из приемов преобразования алгебраических уравнений. Решение уравнений 1 й и 2 й степеней известно еще … Иллюстрированный энциклопедический словарь

АЛГЕБРА — (араб.) часть математики, развивающаяся в связи с задачей о решении алгебраических уравнений. Решение уравнений 1 й и 2 й степеней известно еще с древности. В 16 в. итальянскими математиками найдены решения уравнений 3 й и 4 й степеней. К.… … Большой Энциклопедический словарь

АЛГЕБРА — АЛГЕБРА, алгебры, мн. нет, жен. (от араб.). Отдел математики, часть математического анализа (см. анализ). Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

Источник

Вот зачем нужна школьная алгебра

Обычно на вопрос «зачем нужна математика?» отвечают что-то вроде «гимнастика для ума». На мой взгляд, этого объяснения недостаточно. Когда человек выполняет физические упражнения, то он знает точное название групп мышц, которые при этом развиваются. Но разговоры про математику остаются слишком абстрактными. Какие конкретно «мышцы ума» тренируются школьной алгеброй? Она ведь совсем не похожа на настоящую математику, в которой делаются великие открытия. Что дает умение искать производную каких-то запутанных функций?

Преподавание программирования слабым студентам привело меня к более точному ответу на вопрос «зачем?». В статье я постараюсь донести его вам.

В данном примере от ученика ожидают, что он вспомнит формулу квадрата суммы

В более сложных случаях, полученное выражение можно использовать для других преобразований. Например:

преобразуется сначала в

Чтобы добиться такого результата, ученику нужно распознать в исходном выражении и потом применить три формулы:

Это практически определение рефакторинга из одноименной книги Мартина Фаулера.

В своем труде, автор формулирует их следующим образом:

Рефакторинг (Refactoring) (сущ.): изменение во внутренней структуре программного обеспечения, имеющее целью облегчить понимание его работы и упростить модификацию, не затрагивая наблюдаемого поведения.

Производить рефакторинг (Refactor) (глаг.): изменять структуру программного обеспечения, применяя ряд рефакторингов, не затрагивая его поведения.

В книге даются «формулы», которые нужно распознать в исходном коде и правила их преобразования.

В качестве простейшего примера, приведу «введение поясняющей переменной» из книги:

Части выражения нужно записать в переменную, имя которой поясняет его назначение.

Представьте себе человека, который не может упрощать алгебраические выражения с использованием формулы квадрата суммы и разности квадратов.

Как вы думаете, сможет ли этот человек рефакторить код?

Сможет ли он вообще написать понятный другим людям код, если у него не сформирован идеал этой самой лаконичности? На мой взгляд — нет.

Однако в школе учатся все, а программистами становится меньшинство. Полезен ли навык преобразования выражений для обычных людей? Я думаю да. Только навык применяется в более абстрактном виде: нужно оценить ситуацию и выбрать дальнейшее действие так, чтобы приблизиться к цели. В педагогике этот феномен называется перенос (навыка).

Даже при езде на автомобильном транспорте, водитель постоянно занимается распознаванием шаблонов в окружающем мире и выполнением соответствующих маневров, чтобы добраться до цели.

Когда ты умер, ты об этом не знаешь, только другим тяжело. То же самое, когда ты не освоил математику…

Что же происходит, если человеку не удалось освоить преобразование выражений? Время от времени я веду индивидуальные занятия со студентами, у которых в школе было плохо с математикой. Как правило, они напрочь застревают на теме про циклы. Настолько, что с ними приходится заниматься «алгеброй», но на языке программирования.
Это происходит потому, что при написании циклов основной прием как раз и заключается в том, чтобы преобразовать группу одинаковых выражений.

Допустим результат работы программы должен выглядеть так:

Введение
Глава 1
Глава 2
Глава 3
Глава 4
Глава 5
Глава 6
Глава 7
Заключение

Тривиальная программа для достижения этого результата выглядит так:

Но это решение далеко от лаконичного идеала. Сначала в нем нужно найти повторяющуюся группу действий и потом преобразовать. В итоге получится такое решение:

Если же человек в свое время не освоил математику, то и выполнять подобные преобразования он не сможет. У него просто не будет соответствующего навыка. Именно поэтому тема циклов — первое препятствие в обучении разработчика.

Похожие проблемы возникают и в других областях. Если человек не умеет использовать подручный инструмент, то он не сможет проявлять бытовую смекалку. Злые языки будут говорить, что руки не из того места растут. На дороге это проявляется в неумении правильно оценить ситуацию и выбрать маневр. Что иногда может привести к трагическим последствиям.

Источник