в чем различие принципов относительности галилея и эйнштейна

Чем отличаются принципы относительности Галилея и Энштейна

у Эйнштейна там всё оригинальнее

замедления времени, искривления пространства

Теория относительности была впервые изложена Галилео Галилеем в его «Диалоге о двух главнейших системах мира» в 1632 году.

Теория же относительности утверждает, что все тела находятся в движении относительно друг друга и что определение тела как находящегося «в покое» суть чистая условность. Отсюда следует, что скорость того или иного тела нельзя выразить как абсолютную — только как
«относительную» чему-то другому.

Итальянский астроном и философ Галилео Галилей был также одним из основоположников современной физики. Он более всего известен как человек, поддержавший теорию Коперника (или Аристарха) о том, что Земля
вращается вокруг Солнца.

Католическая церковь посчитала гипотезу еретической и подвергла ученого суду инквизиции. Однако Галилей вовсе не сгнил в кишащем крысами каземате за свои принципы. Срок заключения он отбывал в роскошном доме архиепископа Сиенского, после чего Галилею разрешили вернуться под комфортабельный домашний арест на свою виллу недалеко от Флоренции. Лишь
в 1992 году Церковь официально признала, что как бы ошиблась насчет Галилея и взгляды ученого на строение Солнечной системы были все-таки верными.

Альберт Эйнштейн понимал, что Галилей допустил ошибку в своей теории относительности, — точнее, что теория «разваливалась» в исключительных обстоятельствах.

Источник

чем отличается относительность Галилея и относительность Эйнштейна?

Все правильно написал Остап.
В соответствии с принцип относительности Галилея механическое движение во всех инерциальных системах отсчетах, описывается одними и теми же законами. Во всех инерциальных системах отсчета время одинаково, а координаты преобразуются по формуле:
x(2) = x(1) + v(1,2)*t, x(1) – значение координаты в системе отсчета 1, x(2) – значение координаты в системе отсчета 2, v(1,2) –скорость движения 2-й системы относительно 1-й системы.

Согласно принципу относительности Эйнштейна все законы физики, в том числе и законы электродинамики записываются одинаково в инерциальных системах отсчета. Координаты и время при этом преобразуется в соответствии с формулами Лоренца, которые можно найти в любом учебнике, поэтому приводить их здесь не будем.

PS/ Если говорить о лубке, который представил в своем ответе Сергей Петров, то речь идет об историческом недоразумении. В действительности, принцип относительности Галилея был сформулирован через несколько лет, после публикации первых работ по специальной теории относительности. Противники релятивисткой теории сформулировали свой принцип, назвав его в честь Галилея. Сам же Галилей слыхом не слыхивал о принципе и преобразованиях своего имени. Борьба сторонников и противников ТО закончилось победой первых. Усилия вторых в науке остались в виде более четких формулировок законов классической механики. Как говорится и их труд не пропал, так появился принцип относительности Галилея в ответ на принцип относительности Эйнштейна.

Оказывается, чтобы прослыть гением всех времён, нужно просто повторить то, что до тебя уже однажды придумали.
И плюс немножечко денег.
И минус совесть.

Эйнштейн распространил галилеев принцип относительности механического движения на все физические явления.

Источник

Принципы относительности Галилея и Эйнштейна. Специальная теория относительности

ЛЕКЦИЯ 20

Рассмотрим некоторую инерциальную систему отсчета и другую систему отсчета , движущуюся относительно с постоянной скоростью . Для простоты будем считать, что в начальный момент времени обе системы координат совпадают и скорость направлена вдоль оси . Тогда в дальнейшем оси и будут совпадать, а оси , будут оставаться параллельными друг другу (рис. 1). Пусть в момент (в классической механике) материальная точка находится в поло-жении с радиусами-векторами и в системах и соответственно. Тогда получим

, .

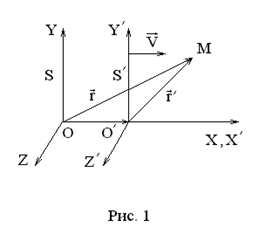
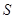
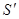
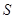
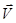
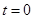
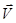
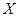
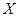
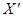
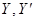
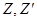
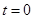
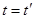
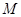
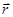
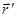
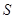
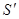
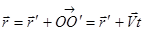
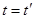
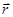
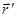
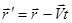
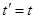
Эти соотношения называются преобразованиями Галилея. Если выразить через , то получим обратные преобразования Галилея

, .

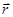
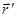
При получении этих соотношений кроме абсолютности времени предполагалась также и абсолютность пространства, так как мы складывали векторы и , измеренные в разных системах отсчета.

Принцип относительности Галилея (в современной формулировке).

Уравнения Ньютона для материальной точки, а также для системы материальных точек одинаковы во все инерциальных системах отсчета (инвариантны относительно преобразований Галилея).

Принцип относительности Эйнштейна.

Законы природы, по которым изменяются состояния физических систем, не зависят от того, к какой из инерциальных систем отсчета относятся эти изменения.

Гипотеза мирового эфира.

В XIX в. получила широкое распространение гипотеза, согласно которой все пространство заполнено особой средой – эфиром. Эфир абсолютно неподвижен и не участвует в движении тел. При этом электромагнитные явления рассматриваются как некоторые процессы в такой среде. В частности, световые волны представляются в виде колебаний эфира, подобно звуко-вым волнам в упругой среде. 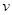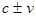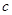При таком описании, скорость света по отношению к телам движущимся относительно эфира со скоростью может принимать значения , где — скорость света относительно неподвижных тел, то есть должен возникать так называемый эфирный ветер. В опытах Майкельсона и Морли (1881 г. и 1887 г.) было показано, что никакого эфирного ветра нет. В них в качестве движущегося тела выступала сама Земля, а возможные изменения скорости света определялись по интерференционной картине в интер-ферометре. В дальнейшем этот результат был сформулирован в виде следующего постулата.

Скорость распространения света в вакууме не зависит от источника света и одинакова во всех направлениях.

Независимость скорости света от движения системы отсчета приводит к необходимости изменения классических представлений о пространстве и времени. Это можно проиллю-стрировать, например, с помощью следующего парадокса. Рассмотрим две инерциальные системы отсчета и , совпадающие друг с другом в некоторый момент времени. Пусть в этот момент источник в точке испускает световой импульс. Тогда в системе световое излучение достигнет сферы , а в системе — сферы (рис. 2). Это говорит о том, что события одновременные в системе (достиже-ние излучением сферы ) являются неодновременными в системе . Следовательно, при переходе от одной инерциальной системы отсчета к другой время должно преобразовывать-ся вместе с координатами. Преобразования, которые сохраняют скорость света постоянной, но учитывают кроме изменения координат и изменение времени были получены Лоренцем. Мы приведем их для случая инерциальных систем, представленных на рис. 1.

, , , , .

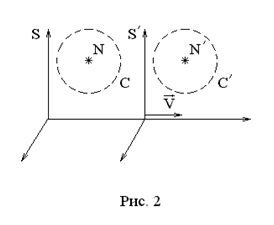
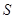
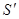
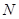
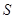
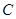
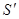
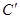
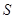
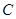
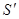
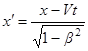
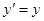
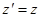
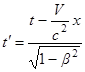
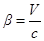
Обратные преобразования Лоренца:

, , , .

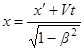
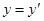
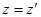
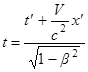
При 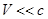преобразования Лоренца переходят в преобразования Галилея, то есть выполняется принцип соответствия.

Принцип относительности, постулат о постоянстве скорости света и преобразования Лоренца легли в основу специальной теории относительности Эйнштейна (1905 г.), описывающей движение тел при скоростях, сравнимых со скоростью света. Специальной она называется потому, что справедлива только в инерциальных системах отсчета. Для случая произвольных систем отсчета Эйнштейном в дальнейшем была создана общая теория относительности, или релятивистская теория гравитации.

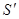
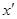
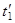
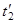
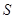
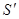
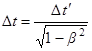
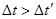
Одним из эффектов теории относительности является замедление хода часов в движущейся системе отсчета. Если в в точке произошли два события в моменты времени и , то из преобразований Лоренца следует, что интервалы между этими событиями в и связаны соотношением

, то есть .

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

В чем различие принципов относительности галилея и эйнштейна

В чем отличие теорий относительности Галилея и Эйнштейна? отличие эйнштейн теория относительность галилей

В современной физике известны два принципа относительности: Птолемея – Коперника и Галилея – Эйнштейна. О принципе Птолемея-Коперника говорят тогда, когда одно и то же явление природы описывается (рассматривается) в различных системах отсчёта. Суть принципа состоит в утверждении, что явления природы объективны, то есть обладают самостоятельной сущностью, а, следовательно, не зависят от систем отсчёта, в которых могут наблюдаться. Тогда как принцип относительности Галилея – Эйнштейна утверждает, что все физические явления, без каких-либо исключений, при одинаковых начальных условиях, протекают одинаково во всех инерциальных системах отсчёта.

Вас только на». «хватило?))

у Птолемея и Каперника разные взгляды на строение солнечной системы. а теория относительности это другое вы запутались,еще раз прочитайте

Запутались Наташа Вы.

а у вас какая позиция?вы считаете что правильным?

2-3,такого примера не может существовать.За всё известное время,официальная «наука» на 100% была и есть против человека.

«все законы природы одинаковы во всех инерциальных системах отсчёта»
Частным случаем принципа относительности Эйнштейна является принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов классической механики подразумевая применимость преобразований Галилея и оставляя открытым вопрос о применимости принципа относительности к оптике и электродинамике.

Коперник, Бруно, Галилей
Не знали эволюции синтеза
Путем холодных облаков,
Где их ядро не велико,
Образовав в тепле высоком,
Ядро частиц. Недалеко,
Там где сливаются протоны
Весь смысл движенья вещества
Освободив свое скопленье,
Найдя в фотонах искупленье
Путем свободного родства.

Источник

Принцип относительности Галилея. Принцип относительности Эйнштейна. Инвариантность интервала между событиями.

Принцип относительности Галилея был сформулирован для классической механики и заключается в следующем:

Физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.

Для справки сразу же нужно отметить, что физические величины не изменяющие своих значений при переходе из одной системы координат в другую с использованием какого-либо преобразования называются инвариантами относительно примененного преобразования.

Уравнения, которые остаются неизменными при переходе из одной системы отсчета в другую, называются инвариантными.

Пусть есть инерциальная система S и движущаяся относительно ее с постоянной скоростью система S’. Предположим, что известен закон движения материальной точки в системе S. Задача нахождения движения этой точки в системе S’ решается с помощью преобразования Галилея. В момент времени точки начала координат О и О’ совпадают и оси координат (X,Y,Z и X’,Y’,Z’) параллельны друг другу. Система S’ движется вдоль оси Z. В момент времени t точка М и системы координат S и S’ расположены так, как показано на рисунке.

В проекциях примет вид , , , . В обратной форме . А в проекциях , , — эти формулы и являются преобразованием Галилея.

Преобразование Галилея справедливо в случае, если .

Если продифференцировать уравнение по времени, то можно получить нерелятивистский закон сложения скоростей, который имеет следующий вид:

.

Ускорение инвариантно относительно преобразования Галилея

Если это уравнение продифференцировать по времени еще раз, то полученный результат покажет, что ускорение инвариантно относительно проеобразования Галилея.

, из чего действительно видно, что , где — ускорение в системе S, а — ускорение в системе S’.

Т.е. при переходе из одной системы отсчета к другой мы использовали преобразование Галилея. Ускорение при этом не измениловь. Значит можно сделать вывод, что ускорение инвариантно относительно примененного преобразования.

Принцип относительности Эйнштейна

Законы природы, по которым изменятся состояния физических систем, не зависят от того, к какой из инерциальных систем отсчета относятся эти изменения.

Все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.

Принцип относительности Энштейна представляет собой более общее определение принципа относительности Галилея. Если принцип относительности галилея был сформулирован только для класической механики, то принцип относительности Энштейна касается всех физических процессов происходящих в природе.

Инвариантность интервала между событиями.

Каждому событию соответствует точка пространства Минковского, в лоренцевых (или галилеевых) координатах. Координаты этой точки задаются тремя декартовыми координаты трёхмерного евклидова пространства. — четвертая координата, в которой ― скорость света, а ― время события. Связь между пространственными расстояниями и промежутками времени, разделяющими события, характеризуется квадратом интервала:

.

Интервал в пространстве Минковского играет роль, аналогичную роли расстояния в геометрии евклидовых пространств. Он инвариантен при замене одной инерциальной системы отсчета на другую, так же, как расстояние инвариантно при поворотах, отражениях и сдвигах начала координат в евклидовом пространстве. Роль, аналогичную роли вращений координат в случае евклидова пространства, играют для пространства Минковского преобразования Лоренца. Квадрат интервала аналогичен квадрату расстояния в евклидовом пространстве. В отличие от последнего квадрат интервала не всегда положителен, также между различными событиями интервал может быть равен нулю.

Инвариантность интервала между событиями.

В дорелятивистской физике пространство и время считались независимыми друг от друга. Расстояние между двумя точками и время между двумя событиями считались постоянными, независимо от системы отсчета, т.е. эти величины были инвариантными при переходе от одной системы к другой. В релятивистской физике появилась зависимость между временем и пространством и остался лишь один пространственно-временной инвариант:

.

Его можно получиить применив преобразования Лоренца.

Вводим переменную , теперь время как бы имеет те же единицы измерения, что и расстояние и можно записать

.

Принимая во внимание и другие координаты

.

В этом выражении мы не привязаны к ориентации осей и направлению движения систем, однако имеется в виду, что в момент времени начало координат одной системы отсчета совпадало с началом координат другой системы отсчета . Запишем:

обозначает разность между пространственными и временными координатами двух событий. Теперь ограничений нет.

– интервал между рассматриваемыми событиями, и пространстве Минковского считается инвариантным.

Источник