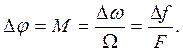в чем отличие чм и фм радиосигнала
Теория радиоволн: аналоговая модуляция
Амплитудная модуляция
При амплитудной модуляции, огибающая амплитуд несущего колебания изменяется по закону, совпадающему с законом передаваемого сообщения. Частота и фаза несущего колебания при этом не меняется.
Одним из основных параметров АМ, является коэфициент модуляции(M).
Коэффициент модуляции — это отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений(%).
Проще говоря, этот коэффициент показывает, насколько сильно значение амплитуда несущего колебания в данный момент отклоняется от среднего значения.
При коэффициенте модуляции больше 1, возникает эффект перемодуляции, в результате чего происходит искажение сигнала.
Данный спектр свойственен для модулирующего колебания постоянной частоты.
На графике, по оси Х представлена частота, по оси У — амплитуда.
Для АМ, кроме амплитуды основной частоты, находящейся в центре, представлены также значения амплитуд справа и слева от частоты несущей. Это так называемые левая и правая боковые полосы. Они отнесены от частоты несущей на расстояние равное частоте модуляции.
Расстояние от левой до правой боковой полосы называют ширина спектра.
В нормальном случае, при коэффициенте модуляции
Аналитическое сравнение ФМ и ЧМ.
Полученные результаты для наглядности сведем в таблицу. Сопоставляя выражения таблицы 1, легко установить различие между ФМ в ЧМ и обратно ЧМ в ФМ.
| ЧМ | ФМ |
Определение: 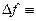 UF (1) Девиация фазы: UF (1) Девиация фазы: 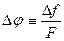 (3) (3) | Определение: 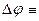 UF (2) Девиация частоты: UF (2) Девиация частоты: 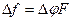 (4) (4) |
Как видно, при ФМ девиация фазы зависит от амплитуды модулирующего напряжения, но зато девиация частоты зависит от обоих параметров модулирующего сигнала, т.е. от его амплитуды и частоты. При ЧМ, наоборот, девиация частоты зависит только от амплитуды, но зато девиация фазы зависит как от амплитуды, так и от частоты модулирующего напряжения.
Если в выражении (2.13) зафиксировать F, то 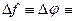
Максимальную девиацию фазы при ФМ называют индексом фазовой модуляции
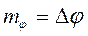
Амплитуду девиации фазы при ЧМ называют также индексом частотной модуляции М:
Методы превращения ФМ в ЧМ и ЧМ в ФМ вытекают из сопоставления накрест лежащих выражений в таблице 1. Формула (4) показывает фактическую зависимость, а формула (1) – требуемую для превращения ФМ в ЧМ. Аналогично для получения ФМ из ЧМ следует формулу (3) превратить в (2).
Для простоты математических преобразований предположим, что модулирующий сигнал изменяется по закону синусоиды при ФМ и по закону косинусоиды – при ЧМ.
Имеем выражение для текущего значения фазы при ФМ
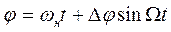
и для текущего значения частоты при ЧМ
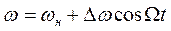
Определим закон изменения частоты при ФМ и фазы при ЧМ. Текущее значение частоты при ФМ получается равным
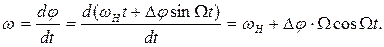
Выражение перед косинусом представляет собой амплитуду девиации частоты при ФМ
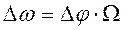
Текущее значение фазы при ЧМ
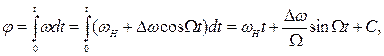
где 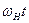
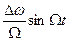
С – постоянная интегрирования; С= 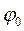
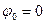
В формуле (2.11) выражение перед синусом является амплитудой девиации фазы при ЧМ:
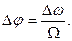
Наибольший интерес представляют выражения (2.10) и (2.12). Переходя в них к циклическим частотам, получим:
амплитуда девиации частоты при ФМ
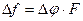
амплитуда девиации фазы при ЧМ
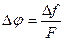
Выражение для мгновенного значения амплитуды ЧМ(ФМ) сигнала при модуляции одним тоном выглядит следующим образом:
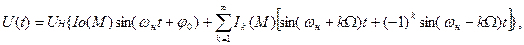
где Uн – амплитуда ВЧ сигнала без модуляции (М=0);
Iк (М) – функции Бесселя порядка К от аргумента равного индексу модуляции М.
Из выражения (2.15) следует, что спектр симметричен (к = 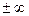
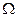
Теоретически спектр ЧМ колебания бесконечно широк, но, учитывая монотонное убывание боковых, его можно ограничивать в пределах полосы, определяемой как:
Пчм=2F (1+M+ 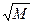
Для радиовещательных РПДУ с ЧМ максимальная девиация частоты установлена 50 Гц и верхняя граница спектра звукового сигнала F=15 кГц. При этом индекс частотной модуляции М= 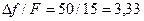
В системах низовой радиосвязи часто применяют узкополосную ЧМ, имеющую индекс модуляции М 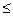
Дата добавления: 2016-02-04 ; просмотров: 2417 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Сравнение различных видов модуляции (AM, ЧМ и ФМ)
Страницы работы
Содержание работы
2.5. Сравнение различных видов модуляции
Сравнивая между собой AM, ЧМ и ФМ, применяющиеся при частотном разделении каналов, можно сделать следующие выводы:
наименьший по ширине спектр в линии занимается при AM, когда для каждой передачи необходим диапазон частот, равный 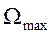
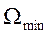
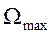
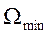
влияние помех, появляющихся в тракте передачи, при ЧМ и ФМ значительно меньше, чем при AM, так как на приемном конце канала включаются ограничители амплитуд. Это позволяет эффективно бороться с помехами, а влияние линейных помех на изменение мгновенной частоты или фазы несущих колебаний обычно достаточно мало. Это определяет широкое применение ЧМ и ФМ на линиях связи, подверженных влиянию помех, но пропускающих достаточно широкий спектр частот. К таким линиям относятся каналы радиосвязи и в первую очередь каналы коротковолновых и ультракоротковолновых (УКВ) радиосвязей. Управление частотой или фазой электрических колебаний нашло широкое применение в телеграфии и передаче данных, где необходимо обеспечить высокую верность передачи при сравнительно низких уровнях сигнала.
При сравнении импульсных систем модуляции можно отметить следующее.
Амплитудно-импульсный способ модуляции применяется в том случае, если простыми средствами удается обеспечить требуемое превышение уровня сигнала над помехой, например, в аналоговой части систем передачи с ИКМ.
Широтно- и фазово-импульсные системы, при которых по каналу передаются импульсы постоянной амплитуды, позволяют применять на приемной станции ограничитель амплитуд и тем самым ликвидировать или значительно ослабить влияние линейных помех. Эти системы требуют широкого спектра передаваемых частот, что является большим недостатком.
Импульсно-кодовая и дельта-модуляции обладают рядом преимуществ по сравнению с другими импульсными системами модуляции (более узкий занимаемый спектр, лучшая помехозащищенность и т. д.).
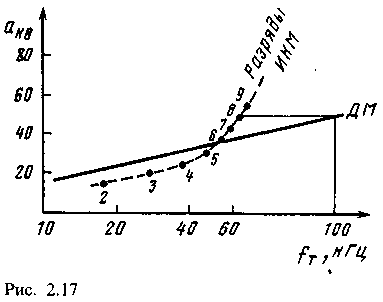
На рис. 2.17 приведена зависимость акв фиксирующего логарифм отношения мощности сигнала и искажений для систем с ДМ и систем с ИКМ. Очевидно, что использование ДМ выгодно только при весьма малых значениях акв. При восьмиразрядной ИКМ тактовая частота 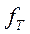
Преимущества систем с ИКМ позволяют считать их наиболее перспективными как в области использования на соединительных линиях, так и при организации междугородной связи в сетях связи железнодорожного транспорта. При этом, однако, возникает ряд проблем, в частности, при создании группового цифрового канала для организации технологических связей из-за усложнения промежуточных пунктов выделения каналов.
Значительные осложнения возникают вследствие наличия в ‘ кабельных линиях специальных цепей СЦБ, по которым передаются неотфильтрованные импульсы постоянного тока большой мощности, имеющие весьма широкий спектр частот, что создает большие импульсные помехи, значительно снижающие устойчивость систем передачи с ИКМ. Требуются специальные устройства, снижающие мешающее действие этих помех.
Тяговые токи и электросети подвижного состава также создают импульсные помехи, к которым системы с ИКМ наиболее чувствительны.
Ведутся интенсивные работы по уменьшению указанных влияний, в результате которых системы передачи с ИКМ будут с успехом применяться в сетях связи железнодорожного транспорта.
1. Почему при частотной модуляции не обходимо сначала проинтегрировать выражение 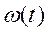
2. Как физически объяснить наличие отрицательного знака при J0(M), если М > 2,3 в выражении ЧМ сигнала?
3. Сформулируйте основные преимущества и недостатки ИКМ. Чем определяется ее перспективность?
4. Какой из способов: ЧИМ, ШИМ, ФИМ требует более широкого спектра частот и почему?
Радиосвязь
Что бы понять, что такое модуляция, нужно знать, что такое частота, с этого и начнём.
Для примера возьмём качели: частота качания качелей, это число полных колебаний, качелей в секунду.
Полных, это значит что одно колебание, это движение качели от самого крайнего левого положения, вниз, через центр до самого максимального уровня справа и потом опять через центр до того же уровня слева.
Обычные дворовые качели имеют частоту порядка 0,5 герца, значит что полное колебание они совершают за 2 секунды.
Динамик звуковой колонки качается гораздо быстрее, воспроизводя ноту «Ля» первой октавы (440 герц), он совершает 440 колебаний в секунду.
В электрических цепях колебания, это качание напряжения, от максимального положительного значения, вниз, через ноль напряжения до максимального отрицательного значения, вверх, через ноль опять до максимального положительного. Или от максимального напряжения, через некое среднее до минимального, потом опять через среднее, опять до максимального.
На графике (или экране осциллографа) это выглядит так:
Что бы сделать модуляцию наглядной, выдумаем два неких сигнала, один частотой 1000Гц, второй 3000Гц, графически они выглядят так:
Заметим, как отображены эти сигналы на графиках слева. Это графики частоты и уровня. Чем больше частота сигнала, тем правее будет изображён на таком графике сигнал, чем больше его уровень (мощность), тем выше линия этого сигнала на графике.
И вот именно этот тестовый сигнал мы и будем «подавать» на микрофонный вход нашего вымышленного передатчика, изучая что получается на выходе (на антенне) и как всё это влияет на разборчивость и дальность связи.
О модуляции вообще
Модулированный сигнал несущей на выходе любого передатчика в любом случае (при любой модуляции) получается методом сложения или умножения сигнала несущей на сигнал, который нужно передать, например сигнал с выхода микрофона. Разница между модуляциями лишь в том, что умножается, с чем складывается и в какой части схемы передатчика это происходит.
В плане приёма, тут всё сводится к тому, что бы из принятого сигнала выделить то, чем был модулирован сигнал, усилить это и сделать понятным (слышимым, видимым).
Как можно видеть, при амплитудной модуляции уровень напряжения колебаний высокой частоты (несущей) напрямую зависит от величины напряжения поступающего с микрофона.
Напряжение на выходе микрофона увеличивается, увеличивается и напряжение несущей на выходе передатчика, то есть больше мощности на выходе, меньше напряжение с микрофона, меньше напряжение на выходе. Когда напряжение на выходе микрофона в некой центральной позиции, то передатчик излучает некую центральную мощность (при АМ модуляции в 100% при тишине перед микрофоном 50% мощности).
Глубиной АМ модуляции называется уровень влияния сигнала с микрофона на уровень выходной мощности передатчика. Если виляние 30% то значит самый сильный отрицательный импульс напряжения с микрофона уменьшит уровень несущей на выходе на 30% от максимальной мощности.
А вот так выглядит спектр сигнала с AM модуляцией (распределение его компонентов по частотам):
SSB модуляция (ОБП, однополосная модуляция)
Вот так выглядит SSB на выходе передатчика:
Видно, что этот сигнал мало чем отличается от АМ модуляции. Оно и понятно, SSB это продолжение AM, то есть SSB создаётся из АМ модуляции, из сигнала которой удаляется не нужная боковая полоса и несущая.
Если же взглянуть на спектр сигнала, то разница очевидна:
Соответственно спектр телеграфного сигнала:
При ЧМ модуляции, как и при АМ на выходе передатчика есть и несущая и две боковые полосы, так как частота несущей болтается в такт модулирующему сигналу, отступая от центра:
Для телеграфа тоже не очень важна линейность, там информацию несёт само наличие или отсутствие несущей, а её уровень лишь побочный параметр.
Если слушать АМ на ЧМ приёмник или наоборот, то будет слышно хрюканье, но разобрать о чём речь всё же можно. Если на ЧМ или АМ приёмник послушать SSB, то будет только дикая аудио-каша из «хрю-жу-жу-бжу» и совершенно никакой разборчивости.
На SSB приёмник можно прекрасно послушать CW (телеграф), АМ, а с некоторыми искажениями и ЧМ с малыми индексами модуляции.
Если включаются одновременно две или больше АМ или ЧМ радиостанций на одной частоте, то получается каша из несущих, этакий писк и визг среди которого ничего не разобрать.
Если же включатся два или больше SSB передатчика на одной частоте, то в приёмнике будет слышно всех, кто говорил, так как несущей у SSB нет и биться (смешиваться до свиста) нечему. Слышно всех, так, словно все сидят в одной комнате и разом заговорили.
Если у АМ или ЧМ частота приёмника не точно совпадает с частотой передатчика, то появляются искажения на громких звуках, «подхрипывания».
Если у SSB передатчика частота меняется в такт уровню сигнала (например, аппаратура не тянет по питанию), то в голосе слышно бульканье. Если плавает частота приёмника или передатчика, то звук плавает по частоте, то «бубнит», то «чирикает».
Второй по сложности, это ЧМ аппарат.
По сути ЧМ аппарат уже содержит в приёмнике всё, что нужно для детектирования АМ сигналов, так как у него тоже есть АРУ (автоматическая регулировка усиления) и следовательно детектор уровня принимаемой несущей, то есть по сути полноценный АМ приёмник, только работающий где-то там, внутри (от этой части схемы работает и пороговый шумоподавитель).
С передатчиком будет сложнее, так как почти все его каскады работают в не линейном режиме.
От автора: переделать можно, но никогда в этом не было нужды.
Отличия спектров при ЧМ и ФМ модуляции.
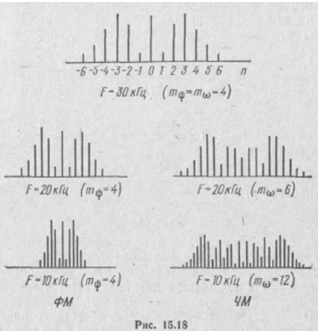
Передача широкополосных ЧМ и ФМ сигналов практически возможна только в диапазоне ультракоротких волн (УКВ). Сравнение спектра ФМ и ЧМ колебаний (рис. 15.18) показывает, что при одинаковых ωн, Ω и т их спектры ничем не отличаются.
Изменения ωн и т вызывают одинаковые изменения в спектрах ФМ и ЧМ колебаний.
Отличительной особенностью спектра ЧМ колебания в сравнении с ФМ является практически независимость его ширины от частоты модуляции. При ЧМ с уменьшением Ω индекс модуляции 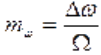

В случае же ФМ индекс модуляции тψ=Δψ не зависит от Ω. Поэтому с изменением Ω число учитываемых гармоник остается неизменным, а ширина спектра меняется: 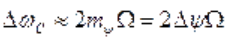
Для ЧМ-сигналов средняя за период высокой частоты мощность постоянна, так как амплитуда колебаний неизменна (Uω1=const). Ширина спектра ЧМ-сигнала, равна 2ωg, зависит только от амплитуды модулирующего сигнала и не зависит от его частоты.
Для ФМ-колебаний средняя за период высокой частоты мощность также неизменна, ибо Uω1=const. Ширина спектра равна 2mW=2ωg, и зависит как от амплитуды модулирующего сигнала, так и от его частоты.
Таким образом, практическая ширина спектра колебаний с угловой модуляцией в m раз больше ширины спектра АМ-колебаний
Нелинейные цепи, классификация. Методы аппроксимации характеристик нелинейных элементов и условия их применимости.
· Резистивные нелинейные цепи – цепи, содержащие хотя бы один резистивный нелинейный элемент и не содержащие реактивных элементов. Процессы описываются нелинейными алгебраическими уравнениями.
· Динамические нелинейные цепи – цепи, содержащие хотя бы один реактивный нелинейный элемент или хотя бы один реактивный элемент. Процессы описываются нелинейными дифференциальными уравнениями.