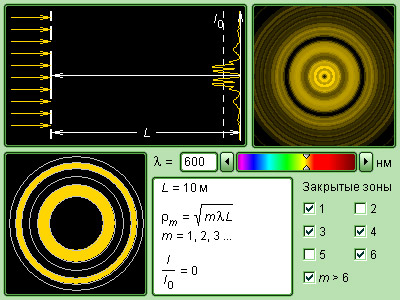
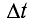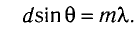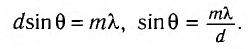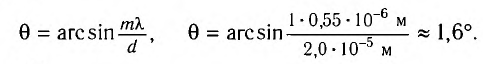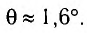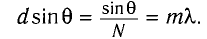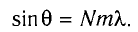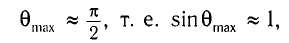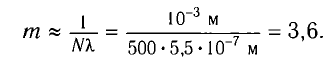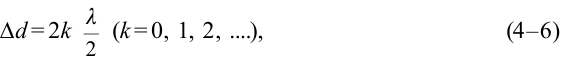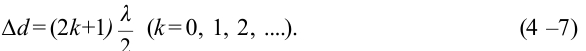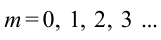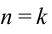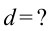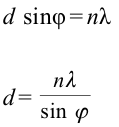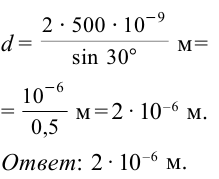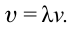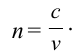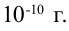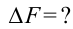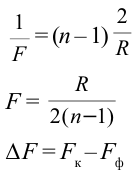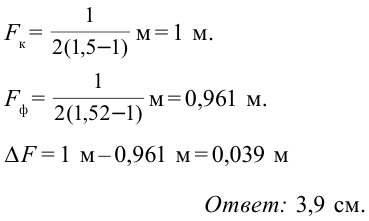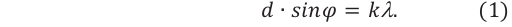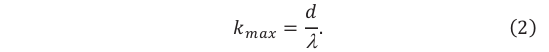в чем измеряется угол дифракции
Основная формула дифракционной решетки
В чем заключаются явления дифракции и интерференции?
Прежде чем рассматривать вывод формулы дифракционной решетки, следует познакомиться с явлениями, благодаря которым это решетка оказывается полезной, то есть с дифракцией и интерференцией.
Оба описанных явления впервые объяснил англичанин Томас Юнг, когда исследовал дифракцию монохроматического света на двух тонких щелях в 1801 году.
Принцип Гюйгенса-Френеля и приближения дальнего и ближнего полей
Математическое описание явлений дифракции и интерференции является нетривиальной задачей. Нахождение точного ее решения требует выполнение сложных расчетов с привлечением максвелловской теории электромагнитных волн. Тем не менее в 20-е годы XIX века француз Огюстен Френель показал, что, используя представления Гюйгенса о вторичных источниках волн, можно с успехом описывать эти явления. Эта идея привела к формулировке принципа Гюйгенса-Френеля, который в настоящее время лежит в основе вывода всех формул для дифракции на препятствиях произвольной формы.
Тем не менее даже с помощью принципа Гюйгенса-Френеля решить задачу дифракции в общем виде не удается, поэтому при получении формул прибегают к некоторым приближениям. Главным из них является плоский волновой фронт. Именно такая форма волны должна падать на препятствие, чтобы можно было упростить ряд математических выкладок.
Следующее приближение заключается в положении экрана, куда проецируется дифракционная картина, относительно препятствия. Это положение описывается числом Френеля. Оно вычисляется так:
Разница между дифракциями Фраунгофера и Френеля заключается в различных условиях для явления интерференции на маленьком и большом расстояниях от препятствия.
Вывод формулы главных максимумов дифракционной решетки, который будет приведен далее в статье, предполагает рассмотрение дифракции Фраунгофера.
Дифракционная решетка и ее виды
Существует два типа дифракционных решеток:
Какой бы ни был тип решетки, идея ее воздействия на волновой фронт заключается в создании периодического возмущения в нем. Это приводит к образованию большого количества когерентных источников, результатом интерференции которых является дифракционная картина на экране.
Основная формула дифракционной решетки
Вывод этой формулы предполагает рассмотрение зависимости интенсивности излучения от угла его падения на экран. В приближении дальнего поля получается следующая формула для интенсивности I(θ):
I(θ) = I0*(sin(β)/β)2*[sin(N*α)/sin(α)]2, где
Пользуясь приведенной формулой, можно рассчитать значение интенсивности для любого угла падения света.
Если находить значение максимумов интенсивности I(θ), то можно прийти к выводу, что они появляются при условии, что α = m*pi, где m является любым целым числом. Для условия максимумов получаем:
Другие способы записи основной формулы для решетки
Заметим, что в приведенной в предыдущем пункте формуле присутствует член sin(θ0). Здесь угол θ0 отражает направление падения фронта световой волны относительно плоскости решетки. Когда фронт падает параллельно этой плоскости, то θ0 = 0o. Тогда получаем выражение для максимумов:
Поскольку постоянная решетки a (не путать с шириной щели) обратно пропорциональна величине d, то через постоянную дифракционной решетки формула выше перепишется в виде:
Чтобы не возникало ошибок при подстановке конкретных чисел λ, a и d в эти формулы, следует всегда использовать соответствующие единицы СИ.
Понятие об угловой дисперсии решетки
Будем обозначать эту величину буквой D. Согласно математическому определению, она записывается следующим равенством:
Физический смысл угловой дисперсии D заключается в том, что она показывает, на какой угол dθm сместится максимум для порядка дифракции m, если изменить длину падающей волны на dλ.
Если применить это выражение для уравнения решетки, тогда получится формула:
Дисперсия угловая дифракционной решетки определяется по формуле выше. Видно, что величина D зависит от порядка m и от периода d.
Чем больше дисперсия D, тем выше разрешающая способность данной решетки.
Разрешающая способность решетки
Под разрешающей способностью понимают физическую величину, которая показывает, на какую минимальную величину могут отличаться две длины волны, чтобы их максимумы на дифракционной картине появлялись раздельно.
Разрешающая способность определяется критерием Рэлея. Он гласит: два максимума можно разделить на дифракционной картине, если расстояние между ними оказывается больше полуширины каждого из них. Угловая полуширина максимума для решетки определяется по формуле:
Разрешающая способность решетки в соответствии с критерием Рэлея равна:
Δθm>Δθ1/2 или D*Δλ>Δθ1/2.
Подставляя значения D и Δθ1/2, получаем:
Это и есть формула разрешающей способности дифракционной решетки. Чем больше число штрихов N на пластинке и чем выше порядок дифракции, тем больше разрешающая способность для данной длины волны λ.
Дифракционная решетка в спектроскопии
Выпишем еще раз основное уравнение максимумов для решетки:
Здесь видно, что чем больше длина волны падает на пластинку со штрихами, тем при больших значениях углов будут появляться максимумы на экране. Иными словами, если через пластинку пропустить немонохроматический свет (например, белый), то на экране можно видеть появление цветных максимумов. Начиная от центрального белого максимума (дифракция нулевого порядка), дальше будут появляться максимумы для более коротких волн (фиолетовый, синий), а затем для более длинных (оранжевый, красный).
Другой важный вывод из этой формулы заключается в зависимости угла θm от порядка дифракции. Чем больше m, тем больше значение θm. Это означает, что цветные линии будут сильнее разделены между собой на максимумах для высокого порядка дифракции. Этот факт уже был освящен, когда рассматривалась разрешающая способность решетки (см. предыдущий пункт).
Описанные способности дифракционной решетки позволяют использовать ее для анализа спектров излучения различных светящихся объектов, включая далекие звезды и галактики.
Пример решения задачи
Покажем, как пользоваться формулой дифракционной решетки. Длина волны света, которая падает решетку, равна 550 нм. Необходимо определить угол, при котором появляется дифракция первого порядка, если период d равен 4 мкм.
Угол θ1 легко рассчитать по формуле:
Переводим все данные в единицы СИ и подставляем в это равенство:
θ1 = arcsin(550*10-9/(4*10-6)) = 7,9o.
Если экран будет находиться на расстоянии 1 метр от решетки, то от середины центрального максимума линия первого порядка дифракции для волны 550 нм появится на расстоянии 13,8 см, что соответствует углу 7,9o.
Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля
Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.
Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.
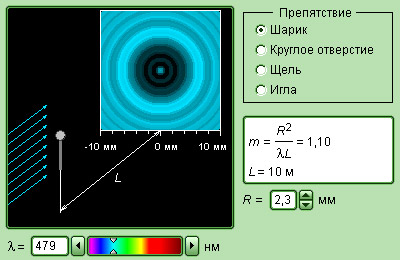
Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.
Принцип Гюйгенса-Френеля
Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в 1818 году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.
Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.
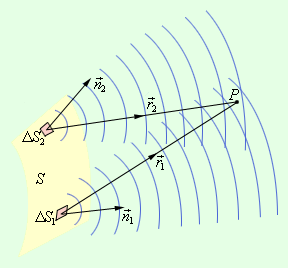
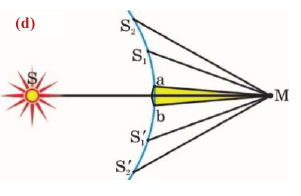
Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.
Предположим, что поверхность S – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновыми фронтами плоской волны считают семейством параллельных плоскостей, которые перпендикулярно направлены относительно распространения волны. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сферам.
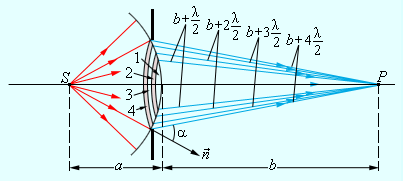
Для примера ниже приведена дифракционная задача прохождения плоской монохроматической волны, которая исходит от удаленного источника через отверстие с радиусом R непрозрачного экрана.
Чтобы расчеты были облегченными, волновая поверхность падающей волны разбивается на кольцевые зоны, называемыми зонами Френеля, исходя из правила: расстояния от границ соседних зон к точке Р имеют отличие на половину волны.
Зоны Френеля. Интерференционный максимум
Отличие от двух соседних точек расстоянием λ 2 говорит о том, что колебания, возбуждаемые этими зонами в состоянии противофазы. Соседние волны начинают гасить друг друга, а это приводит к тому, что суммарная амплитуда в точке запишется как:
Выражения в скобках равняются нулю, значит, амплитуда, вызванная волновым фронтом, равняется половине действий первой зоны.
Полученные пластинки обладают свойством фокусировки света, поэтому их называют зонными пластинками.
Круглый диск дает понять, что при дифракции зоны Френеля от 1 до m будут в закрытом состоянии. Отсюда получаем, что формула амплитуды колебаний примет вид:
Так как оптический диапазон имеет короткую волну, тогда соответственно зона Френеля также мала. Отчетливее проявление дифракционных явлений заметно при небольшом количестве зон на препятствии.
Получим формулы вида:
Когда количество зон Френеля из препятствия увеличивается, тогда дифракционные явления становятся незаметными:
Определение границы применимости геометрической оптики возможно при помощи заданного неравенства. При выполнении данного условия узкий пучок света может быть сформирован.
Отсюда следует вывод, что волновая оптика – это предельный случай геометрической.
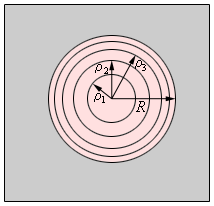
При расчете видно, что радиусы ρ m зон Френеля на волне сферического фронта запишется, как
Выводы по теории Френеля справедливы.
Дифракция и интерференция света применима к любым волнам, так как имеется общность закономерностей. Начало XIX века – это было время, когда ученые только начинали изучать волны, а физическая природа света еще не была раскрыта.
Дифракция света.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: дифракция света, дифракционная решётка.
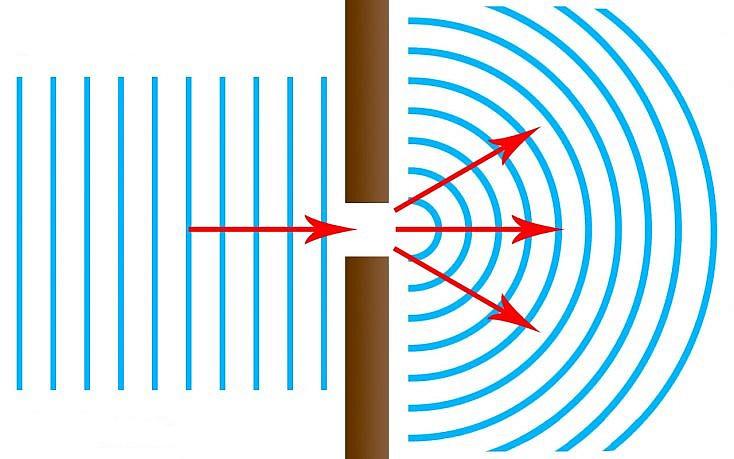
Пусть, например, плоская волна падает на экран с достаточно узкой щелью (рис. 1 ). На выходе из щели возникает расходящаяся волна, и эта расходимость усиливается с уменьшением ширины щели.
 |
| Рис. 1. Дифракция на щели |
Вообще, дифракционные явления выражены тем отчётливей, чем мельче препятствие. Наиболее существенна дифракция в тех случаях, когда размер препятствия меньше или порядка длины волны. Именно такому условию должна удовлетворять ширина щели на рис. 1.
Так, на рис. 2 изображена дифракционная картина, полученная в результате прохождения лазерного луча сквозь небольшое отверстие диаметром 0,2мм.
 |
| Рис. 2. Дифракция лазерного луча на отверстии |
Напоминает интерференцию, не правда ли? Это она и есть; данные кольца являются интерференционными максимумами и минимумами. Какие же волны тут интерферируют? Скоро мы разберёмся с этим вопросом, а заодно и выясним, почему вообще наблюдается дифракция.
Опыт Юнга.
Всякий эксперимент с интерференцией света содержит некоторый способ получения двух когерентных световых волн. В опыте с зеркалами Френеля, как вы помните, когерентными источниками являлись два изображения одного и того же источника, полученные в обоих зеркалах.
Но если Солнце является чрезмерно «большим», то нужно искусственно создать точечный первичный источник. С этой целью в опыте Юнга использовано маленькое предварительное отверстие (рис. 3 ).
 |
| Рис. 3. Схема опыта Юнга |
Томас Юнг осуществил этот эксперимент, измерил ширину интерференционных полос, вывел формулу и с помощью этой формулы впервые вычислил длины волн видимого света. Вот почему этот опыт вошёл в число самых знаменитых в истории физики.
Принцип Гюйгенса–Френеля.
Напомним формулировку принципа Гюйгенса: каждая точка, вовлечённая в волновой процесс, является источником вторичных сферических волн; эти волны распространяются от данной точки, как из центра, во все стороны и накладываются друг на друга.
Но возникает естественный вопрос: а что значит «накладываются»?
В таком виде принцип Гюйгенса не давал ответа на вопрос, почему в процессе распространения волны не возникает волна, идущая в обратном направлении. Не объяснёнными оставались и дифракционные явления.
Модификация принципа Гюйгенса состоялась лишь спустя 137 лет. Огюстен Френель заменил вспомогательные геометрические сферы Гюйгенса на реальные волны и предположил, что эти волны интерферируют друг с другом.
Принцип Гюйгенса–Френеля. Каждая точка волновой поверхности служит источником вторичных сферических волн. Все эти вторичные волны являются когерентными ввиду общности их происхождения от первичного источника (и, стало быть, могут интерферировать друг с другом); волновой процесс в окружающем пространстве есть результат интерференции вторичных волн.
Идея Френеля наполнила принцип Гюйгенса физическим смыслом. Вторичные волны, интерферируя, усиливают друг друга на огибающей своих волновых поверхностей в направлении «вперёд», обеспечивая дальнейшее распространение волны. А в направлении «назад» происходит их интерференция с исходной волной, наблюдается взаимное гашение, и обратная волна не возникает.
В частности, свет распространяется там, где вторичные волны взаимно усиливаются. А в местах ослабления вторичных волн мы будем видеть тёмные участки пространства.
Принцип Гюйгенса–Френеля выражает важную физическую идею: волна, удалившись от своего источника, в дальнейшем «живёт своей жизнью» и уже никак от этого источника не зависит. Захватывая новые участки пространства, волна распространяется всё дальше и дальше вследствие интерференции вторичных волн, возбуждённых в различных точках пространства по мере прохождения волны.
Как принцип Гюйгенса–Френеля объясняет явление дифракции? Почему, например, происходит дифракция на отверстии? Дело в том, что из бесконечной плоской волновой поверхности падающей волны экранное отверстие вырезает лишь маленький светящийся диск, и последующее световое поле получается в результате интерференции волн вторичных источников, расположенных уже не на всей плоскости, а лишь на этом диске. Естественно, новые волновые поверхности теперь не будут плоскими; ход лучей искривляется, и волна начинает распространяться в разных направлениях, не совпадающих с первоначальным. Волна огибает края отверстия и проникает в область геометрической тени.
Дифракционная решётка.
 |
| Рис. 4. Дифракционная решётка |
Дифракционная решётка изготавливается с помощью так называемой делительной машины, которая наносит штрихи на поверхность стекла или прозрачной плёнки. При этом штрихи оказываются непрозрачными промежутками, а нетронутые места служат щелями. Если, например, дифракционная решётка содержит 100 штрихов на миллиметр, то период такой решётки будет равен: d= 0,01 мм= 10 мкм.
Сперва мы посмотрим, как проходит сквозь решётку монохроматический свет, т. е. свет со строго определённой длиной волны. Отличным примером монохроматического света служит луч лазерной указки длина волны около 0,65 мкм).
На рис. 5 мы видим такой луч, падающий на одну из дифракционных решёток стандартного набора. Щели решётки расположены вертикально, и на экране за решёткой наблюдаются периодически расположенные вертикальные полосы.
 |
| Рис. 5. Дифракция лазерного луча на решётке |
Теория дифракционной решётки весьма сложна и во всей своей полноте оказывается далеко за рамками школьной программы. Вам следует знать лишь самые элементарные вещи, связанные с одной-единственной формулой; эта формула описывает положения максимумов освещённости экрана за дифракционной решёткой.
 |
| Рис. 6. Дифракция на решётке |
Интерференционные максимумы наблюдаются в тех случаях, когда разность хода равна целому числу длин волн:
Формула (1) позволяет найти углы, задающие направления на максимумы:
Этот угол задаёт направления на максимумы первого порядка. Их два, и расположены они симметрично относительно центрального максимума. Яркость в максимумах первого порядка несколько меньше, чем в центральном максимуме.
Аналогично, при имеем угол:
Он задаёт направления на максимумы второго порядка. Их тоже два, и они также расположены симметрично относительно центрального максимума. Яркость в максимумах второго порядка несколько меньше, чем в максимумах первого порядка.
 |
| Рис. 7. Максимумы первых двух порядков |
Вообще, два симметричных максимума k-го порядка определяются углом:
С помощью дифракционной решётки можно измерить неизвестную длину волны. Направляем пучок света на решётку (период которой мы знаем), измеряем угол на максимум первого
порядка, пользуемся формулой (1) и получаем:
Дифракционная решётка как спектральный прибор.
Предположим, что на дифракционную решётку падает белый свет. Давайте вернёмся к формуле (2) и подумаем, какие выводы из неё можно сделать.
Положение центрального максимума ( ) не зависит от длины волны. В центре дифракционной картины сойдутся с нулевой разностью хода все монохроматические составляющие белого света. Поэтому в центральном максимуме мы увидим яркую белую полосу.
 |
| Рис. 8. Дифракция белого света на решётке |
Спектральное разложение белого света, даваемое дифракционной решёткой, проще всего наблюдать, глядя на обычный компакт-диск (рис. 9 ). Оказывается, дорожки на поверхности диска образуют отражательную дифракционную решётку!
Содержание:
Дифракция света:
Среда называется однородной, если ее физические свойства по всему объему одинаковы во всех точках пространства. Среда называется изотропной, если ее физические свойства одинаковы по всем направлениям в пространстве.
Закономерности распространения волн любой природы в различных средах носят универсальный характер.
Рассмотрим процесс распространения волн на поверхности воды.
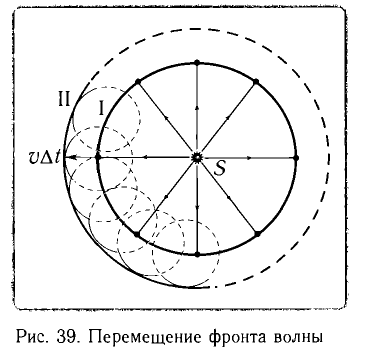
Волны, возбуждаемые точечным источником S, распространяются на поверхности воды по всем направлениям с одинаковой по модулю скоростью v. Следовательно, фронт волны в этом случае будет иметь вид окружности (рис. 39). Соответственно, если волна будет распространяться в однородной изотропной среде по всем направлениям в пространстве, то ее волновой фронт будет иметь вид сферической поверхности.
Как видим из рисунка, если в некоторый момент времени t фронт волны занимал положение I, то через промежуток времени
Общие закономерности процесса распространения волн объяснил Гюйгенс, сформулировав в «Трактате о свете» принцип, позволяющий определить положение волнового фронта с течением времени. Согласно принципу Гюйгенса:
Таким образом, согласно принципу Гюйгенса для нахождения положения волнового фронта через промежуток времени 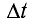
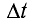
Соответственно, огибающая вторичных волн (1, 2, 3 и т. д.) определяет новое положение волнового фронта в момент t + 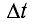
«Линия, перпендикулярная волновому фронту, называется лучом (волновым лучом). Волновой луч определяет направление распространения волны, а также направление переноса энергии волной.
На очень больших расстояниях от точечного источника волны, излучаемые им, можно считать плоскими. Например, световые лучи в приходящем на Землю солнечном излучении являются практически параллельными друг другу.
Принцип Гюйгенса объясняет прямолинейное распространение волн в однородной среде. Поскольку в такой среде радиусы фронтов вторичных волн (v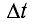
Однако различные волны в однородной среде не всегда распространяются прямолинейно, поскольку наблюдаются отклонения от закона прямолинейного распространения. Действительно, стоя за углом дома, мы хорошо слышим, что едет автомобиль, хотя не видим его, поскольку находимся в области «тени». Таким образом, звуковые волны как бы «заворачивают за угол», в то время как световым волнам этого сделать не удается.
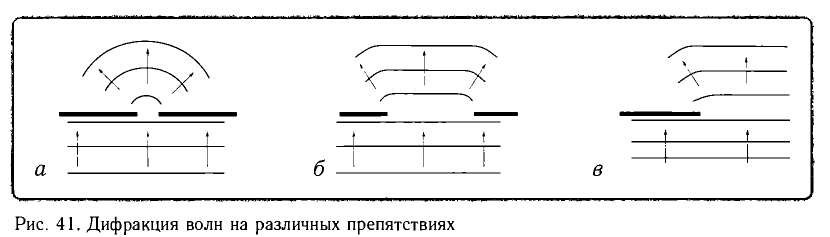
Явление отклонения распространения волн от прямолинейного вблизи краев препятствий и огибания волнами препятствий получило название дифракции (рис. 41).
Явление дифракции служит одним из подтверждений волновой природы наблюдаемого процесса.
Для проявления дифракции размеры препятствий (отверстий) должны быть меньше или сравнимы с соответствующей длиной волны, вот почему в рассмотренном примере звук
( 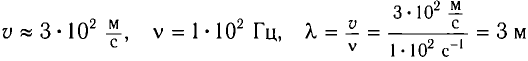
смог «завернуть за угол», а свет, отраженный от автомобиля (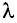
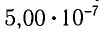
Изучая дифракцию света, французский физик Огюстен Жан Френель дополнил принцип Гюйгенса представлением об интерференции вторичных волн, которые являются когерентными. Принцип Гюйгенса — Френеля позволил охарактеризовать явление дифракции количественно:
Таким образом, согласно Френелю дифракция света объясняется интерференцией вторичных волн от различных участков начального положения волнового фронта.
Для наблюдения дифракции света используется дифракционная решетка.
Дифракционной решеткой называют оптический прибор, предназначенный для очень точного измерения длин волн и разложения света в спектр.
Дифракционная решетка состоит из большого числа равноотстоящих параллельных штрихов (щелей), нанесенных на стеклянную или металлическую поверхность. Длина решеток составляет 10—15 см. Они содержат 10 000—20 000 штрихов на 1 см.
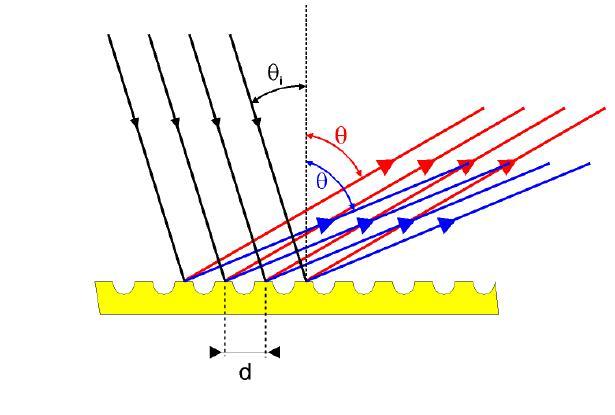
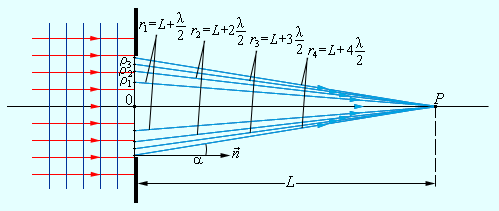
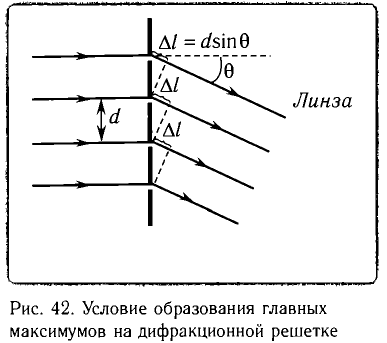
Рассмотрим дифракционную решетку, представляющую собой систему из N одинаковых равноотстоящих параллельных щелей (прозрачные участки) в плоском непрозрачном экране (рис. 42). Если ширина каждой щели b, ширина непрозрачной части между щелями а, то величина d = a + b называется постоянной решетки или ее периодом.
Пусть на решетку, постоянная которой равна d, падает плоская волна, длина которой 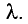
Собирающая линза фокусирует параллельные лучи (вторичные волны) в одну точку на экране, расположенном в фокальной плоскости линзы. Далее вторичные волны, испущенные разными щелями, интерферируют на экране, усиливая или ослабляя друг друга в зависимости от разности хода между ними. Таким образом, на экране получается дифракционная картина в виде системы светлых и темных полос.
Наиболее яркие дифракционные максимумы получили название главных дифракционных максимумов.
Условие образования главных дифракционных максимумов, наблюдаемых под углами 9 с использованием дифракционной решетки, имеет вид:
Полученное условие образования главных дифракционных максимумов имеет наглядный физический смысл: на отрезке, равном разности хода от соседних щелей 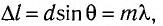
В этом случае вторичные волны от всех щелей решетки приходят в точку наблюдения синфазно (с фазами, отличающимися на число, кратное 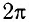
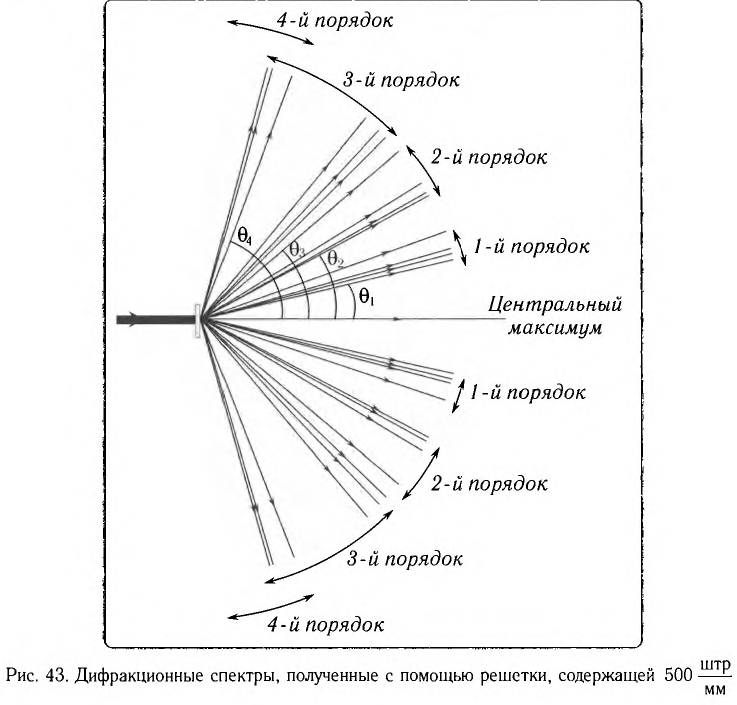
Таким образом, дифракционная картина на экране представляет собой чередующиеся максимумы и минимумы интенсивности излучения. Центральный максимум (m = 0) называется нулевым. Дифракционные максимумы, соответствующие m= 1, образуют спектр первого порядка, m = 2 — спектр второго порядка и т. д. (рис. 43).
Между максимумами интенсивности расположены минимумы, так как при изменении угла 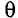
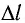
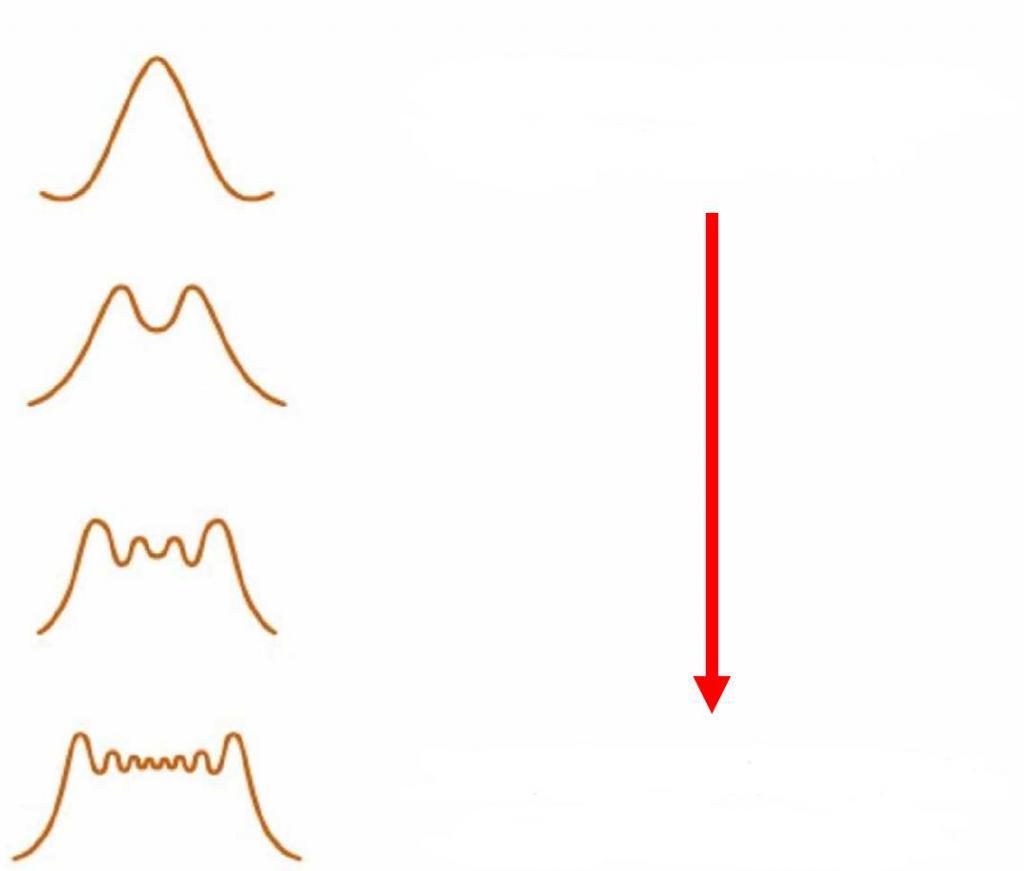
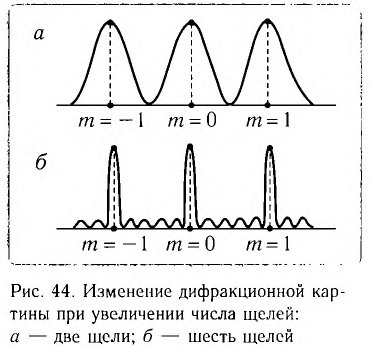
По мере увеличения числа щелей (штрихов) дифракционной решетки максимумы на экране становятся более узкими, а расстояния между ними более широкими (рис. 44). При этом происходит перераспределение энергии падающего излучения, большая часть которой приходится на максимумы.
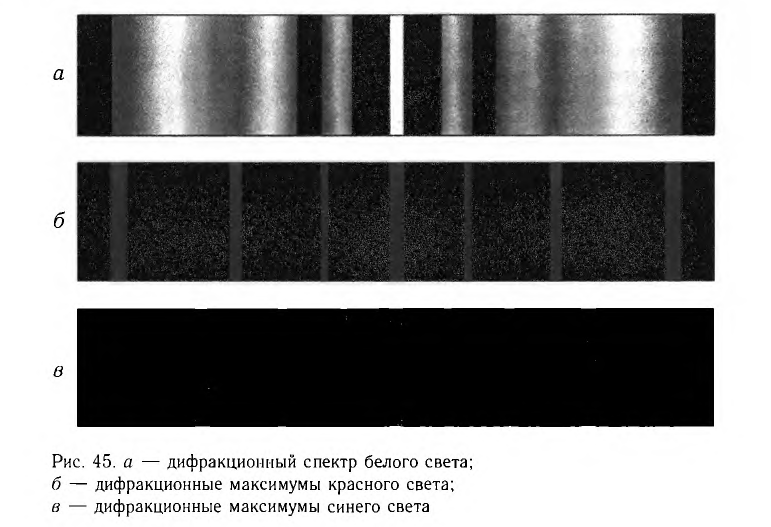
При падении белого света на решетку спектральные максимумы любого порядка (кроме нулевого) содержат все цвета радуги (рис. 45, а).
В дифракционном спектре больше всего отклоняются от начального направления распространения красные лучи (рис. 45, б), меньше всего — синие (рис. 45, в), что и следует из формулы для определения дифракционных максимумов решетки.
Первая дифракционная решетка, сконструированная американским ученым Дэвидом Риттенхаузом, состояла из волосков диаметром около 0,1 мм и длиной 10 мм, натянутых параллельно на расстоянии порядка 0,2 мм один от другого. Немецкий физик Йозеф Фраунгофер вместо волосков использовал штрихи, наносимые на стекло алмазным острием. Их число на 1 мм решетки достигало у него 300.
Направления, в которых наблюдаются минимумы интенсивности при дифракции света на двух щелях, остаются минимумами для дифракции на дифракционной решетке. Однако к ним добавляются минимумы, связанные с интерференцией излучения, идущего от каждой из щелей (см. рис. 44). Эти минимумы легко определить из условия, что разность хода света от соседних щелей в данном направлении должна быть кратна нечетному числу полуволн.
Пример №1
Определите угол отклонения 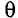
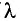
Решение
Условие дифракционных максимумов определяется соотношением
Ответ:
Пример №2
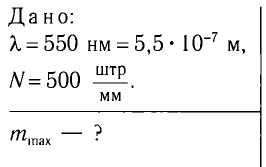
На дифракционную решетку, имеющую N=500 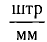
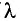
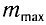
Решение
Условие дифракционных максимумов определяется соотношением
Наибольшее значение 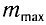
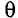
тогда наибольшее значение максимума находится по формуле
Для определения 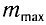
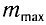
Ответ: 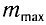
Дифракция света и интерференция
Весной радуемся появлению цветных блесков в воздухе после дождя, на мыльном пузыре, на масле, разлитом на асфальте. Но мы не задумываемся над тем, как они появляются. Причиной этого является интерференция света. Явление интерференции свойственно волнам любой природы. Для осмысления этого явления начнем изучение интерференции механических волн.
При распространении волн в какой-либо среде они ведут себя самостоятельно, как будто нет других волн. Это называется принципом суперпозиции (независимость) распространения волн. Результирующее смещение частицы в пространстве в произвольное время равно геометрической сумме смещения волновых процессов, в которых участвовала частица. Например, если в среде распространяются две волны, то они самостоятельно друг от друга будут действовать на частицу, находящуюся в определенной точке. Если частоты этих волн равны и разница фаз не меняется, то в точке, где они встречаются, они усиливают друг друга или погашают. Это явление называется интерференцией волн. Волны, имеющие равные частоты и у которых разница фаз не меняется, называются когерентными волнами. Явление усиления или погашения друг друга при встрече когерентных волн называется интерференцией волн. В каких случаях они друг друга усиливают или погашают? Для этого рассмотрим встречу волн, выходящих из двух когерентных источников 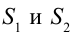
Путь, пройденный волной, вышедшей из источника 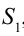
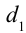
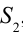
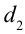
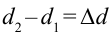
в этой точке наблюдается усиление колебания. Выражение (4-6) называется условием максимума интерференции.
Если разность хода будет кратной нечетному числу длины волны:
В этой точке наблюдается погашение колебания. Выражение (4-7) называется условием минимума интерференции.
Интерференция света является частным случаем интерференции механических волн. Для наблюдения этого явления две световые волны, испущенные двумя когерентными источниками, должны встречаться в одной точке пространства. Однако сколько бы ни выбрали отдельных источников, световые излучения, испущенные ими, не будут когерентными. Поэтому световое излучение, испущенное одним источником, искусственно делят на два излучения и получают когерентные волны.
Метод Юнга (1801 год)
Цвета на тонких пленках
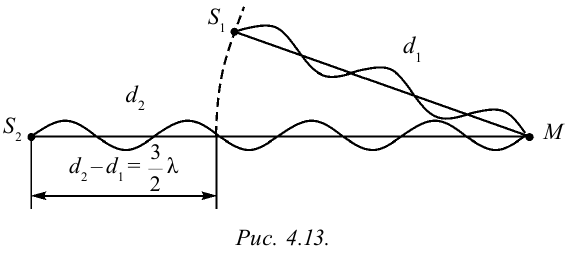
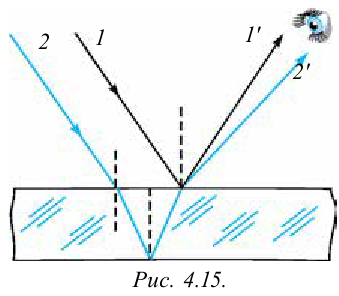
Вернемся к цветам на масле, разлитом на асфальте, и на мыльных пузырях. Белый свет падает на тонкую пленку (рис. 4.15). Часть падающей волны (волна 1) отражается от верхней поверхности пленки. Часть проходит внутрь пленки и отражается от нижней поверхности (волна 2).
Две отраженные волны 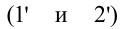
Кольца Ньютона
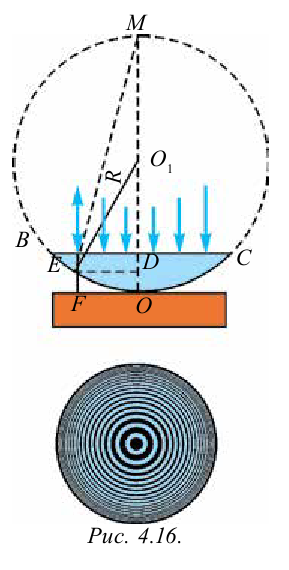
Пусть на тонкую пластину поставлена линза с выпуклой поверхностью (рис. 4.16). Здесь между плоской параллельной пластиной и поверхностью линзы, касающейся ее в точке О, имеется слой воздуха. Свет, падающий на плоскую поверхность линзы, отражается от верхнего и нижнего слоя воздуха. При встрече этих лучей наблюдается интерференция.
Если устройство будет освещено монохроматическим (только одного цвета) лучом, картина интерференции выглядят в форме светлых и темных колец. Если устройство будет освещено белым светом, то будут видны темные пятна в отраженном свете от точки касания линзы с поверхностью. Вокруг нее располагаются цветные кольца. Путем измерения радиуса кольца соответствующего
порядка можно определить длину волны света или радиус кривизны линзы: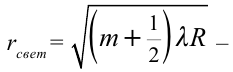
— радиус светлых колец; R радиус кривизны линзы
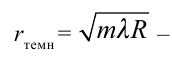
Дифракция света
Люди давно заметили, что свет заходит за края преграды, встречающейся на своем пути. Научное объяснение этого явления первым дал Ф. Грималди. Он объясняет причину того, что тень, которая появляется за предметами, тусклая. Это явление он назвал дифракцией. Таким образом, огибание волнами, встречающими препятствия на своем пути, называется дифракцией волн. При этом не выполняется закон прямолинейного распространения света. Чтобы наблюдалась дифракция, размер преграды должен быть меньше, чем длина падающей на него волны. Дифракцию света также можно увидеть при прохождении света через узкие щели. Здесь размер щели тоже должен быть меньше, чем длина падающей на нее волны.
Для получения четкой и точной дифракционной картины пользуются дифракционной решеткой. Дифракционная решетка состоит из многочисленных преград и щелей, которые пропускают и отражают. Дифракционная решетка по расположению преград делится на два вида: упорядоченные и неупорядоченные дифракционные решетки.
В упорядоченных дифракционных решетках щели расположены в строго определенном порядке. В неупорядоченных дифракционных решетках щели располагаются беспорядочно.
Для изготовления плоской упорядоченной дифракционной решетки берется прозрачная пластина и с помощью лезвия наносятся параллельные и очень близко расположенные друг к другу линии. Нанесенные линии служат как щель, а расстояния между ними как преграда. Пусть ширина щели будет а, ширина преграды в. Тогда 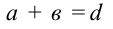
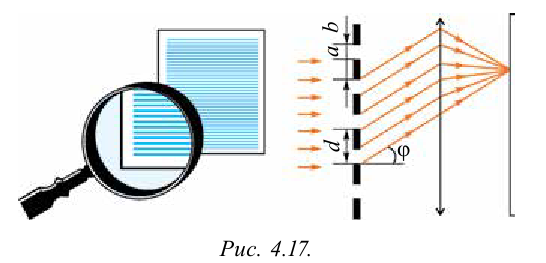
Рассмотрим прохождение света через дифракционную решетку (рис. 4.17).
Пусть монохроматическая волна падает перпендикулярно к поверхности решетки. Вторичные волны, прошедшие через щель, в результате явления дифракции отклоняются на угол ср. Затем собираясь, они направляются на экран. На экране появится дифракционная картина, в виде чередующихся светлых полос, разделенных затемненными промежутками.
При этом постоянная решетки d, длина волны света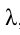
здесь: 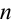
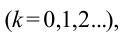
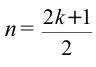
Наблюдаемые явления интерференции и дифракции доказывают, что свет имеет волновые свойства. Эти явления используют в технике. Например, прибор, называемый интерферометром, является очень чувствительным. С его помощью можно точно измерить маленькие углы, определить длину волны света, длину маленьких отрезков, показатели преломления света различных веществ, проверить шероховатость поверхности, а также определить степень блеска.
Пример №3
На дифракционную решетку падает монохроматический свет с длиной волны 500 нм. Если спектр второго порядка наблюдается под углом 30°, чему равна постоянная решетки?
Дано: 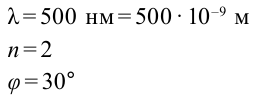
Формула:
Решение:
Дисперсия света и спектральный анализ
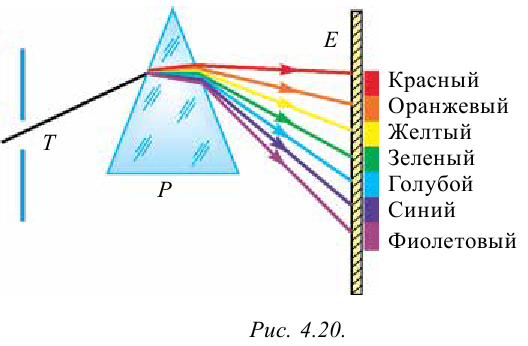
Вопрос о цвете разных тел и веществ интересовал людей с давних времен. Почему Солнце, заходя за горизонт, краснеет? Почему появляется радуга? Почему при прохождении света через некоторые минералы, они блестят? Ответы на подобные вопросы нашлись только во времена Ньютона. В 1666 году И. Ньютон написал о своем эксперименте следующее: «Я при обработке различных оптических стекол для проверки известных явлений по цвету изготовил треугольную стеклянную призму. В этих целях я затемнил комнату и для поступления солнечного луча на окне сделал маленькую дырку. Я расположил призму так, чтобы луч попадал на призму и, отражаясь от нее, собирался на стене. Таким образом, наблюдение полученных разнообразных и усиленных цветов оставили у меня большое удовольствие».
При закрывании щели стеклом красного цвета Ньютон наблюдал на стене только красное пятно, при закрывании щели стеклом зеленого цвета он наблюдал на стене только зеленое пятно. При изучении спектра он установил, что лучи разного цвета преломляются по-разному.
Ньютон не знал причину этого. Но этот эксперимент доказал, что белый цвет является сложным цветом. Он состоит из семи цветов: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. Имеются и другие эксперименты Ньютона, доказывающие, что белый цвет является сложным цветом. Ньютон взял окружность и, разделив ее на секторы, раскрасил их в семь разных цветов. Эту окружность он закрепил на ось вращения двигателя. При определенной скорости вращения разноцветная окружность выглядит как белая.
Если на пути света, разделенного на разные цвета, после прохождение через первую призму поставить призму под углом 180°, она выполняет функцию собирающей линзы. В точке сбора лучей, выходящих из призмы, получается белый цвет (рис. 4.21).
Длина волны световых волн очень короткая. Например, красный луч имеет самую большую длину волны, его значение 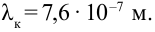
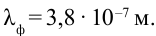
В 1873 году английский ученый Дж. Максвелл теоретически доказал, что свет состоит из электромагнитных волн, распространяющихся со скоростью 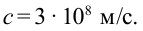
Отсюда можно сделать вывод: лучи, имеющие разные цвета, в среде распространяются с различной скоростью. При переходе света из одной среды в другую меняется его длина волны, но частота не меняется. Нам известно, что скорость волны 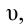
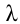
Если учесть связи показателя преломления света 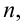
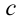
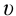
Получается, что показатель преломления луча в среде для разных лучей будет разным.
Зависимость показателя преломления света от длины волны называется дисперсией.
Это объясняет, почему лучи, прошедшие через призму, отклоняются на разные углы. Таким образом, скорость красного луча в любой среде будет больше, чем фиолетового. Например, в воде 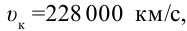
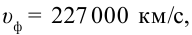
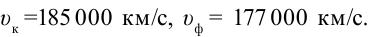
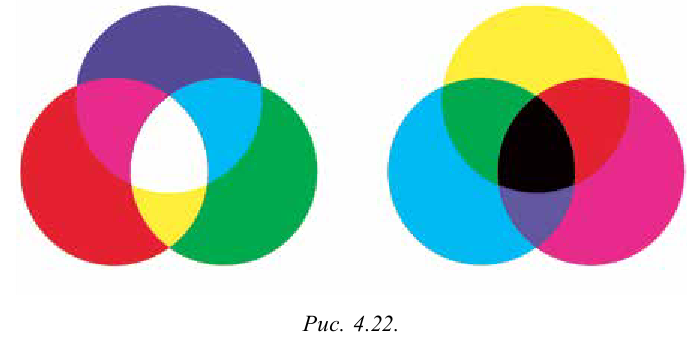
В 1807 году английский физик Томас Юнг, комбинируя красный, зеленый и голубой цвета, доказал, что возможно получить белый цвет. Также, комбинируя красный, зеленый и голубой цвета, можно получить другие цвета (рис. 4.22).
Красный, зеленый и голубой цвета Юнг назвал первичными лучами. Никакой из этих первичных цветов невозможно получить из комбинации других цветов. Это можно легко проверить, освещая экран лучом красного, зеленого и голубого цветов. В том месте, где накладываются эти три цвета, образуется белый цвет.
При смешивании красного и голубого цветов появится темный цвет, при смешивании красного и зеленого цветов появится желтый цвет. В современных телевизорах и на экране компьютера цветное изображение создается благодаря соединению этих трех цветов.
Если через призму пропустить свет из разных источников, никакой из них (кроме лазера) не является монохроматическим, т.е. не излучает волны с одинаковой частотой. Нагретые тела тоже излучают волны разного спектра. Их спектр можно разделить на три вида.
Солнечный спектр или спектр лампы накаливания является непрерывным. Свет, испущенный нагретым веществом в твердом или жидком состоянии и сильно сжатыми газами, имеет непрерывный спектр.
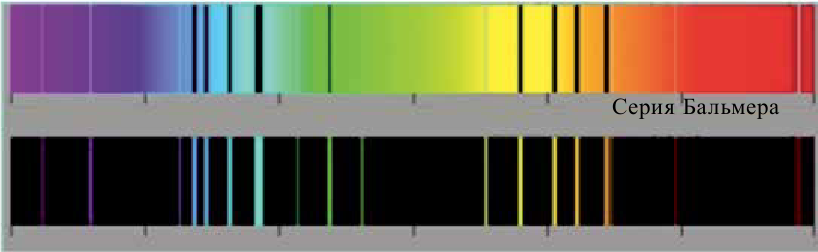
Линейчатый спектр
В таком спектре имеется одна линия. Такой спектр испускает атомы, не связанные друг с другом. Отдельные атомы испускают электромагнитные волны с одной длиной волны.
Полосатый спектр
Отдельные слабо связанные или не связанные молекулы излучают спектр в виде отдельных полос, разделенных темными промежутками. Если поставить красное стекло на пути света, излучаемого лампой, через него проходит только красный свет, а остальные лучи поглощаются. Если белый луч пропустить через неизлучающий газ, то на фоне непрерывного спектра источника появятся черные линии. Причиной этого является поглощение газом лучей некоторых частот. Исследования показали, что нагретое тело испускает свет тех длин волн, которые оно поглащает.
Каждый химический элемент имеет свойственный только ему спектр. Подобно неповторяемости отпечатков пальцев, спектр каждого элемента также не похож на другие.
Определение состава химического вещества по его спектру называется спектральным анализом. Этот метод является очень чувствительным. С его помощью можно обнаружить элемент в составе сложного вещества, если даже его масса не превышает
Такой анализ в основном имеет качественный характер, т.е. можно определить, какие элементы имеются в веществе. Однако определить количественное значение этих элементов сложно. Так как при низких температурах вещества большинство спектральных линий не проявляют себя.
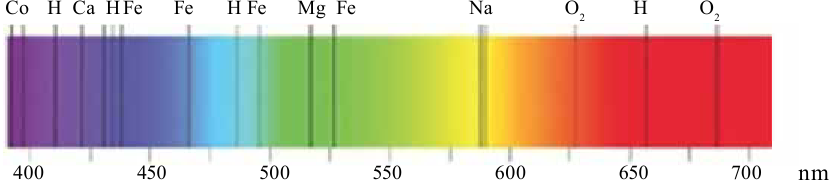
В настоящее время определены спектры всех атомов, составлены их таблицы (рис. 4.23). С помощью спектрального анализа были открыты такие химические элементы, как рубидий, цезий и другие. Слово «цезий» означает «небесно-голубой».
Спектр элемента цинка
Именно благодаря спектральному анализу стало возможным определить химический состав Солнца и звезд. Другими методами его определить невозможно. Следует сказать, что элемент гелий сначала открыли на Солнце, а затем нашли в атмосфере Земли. «Гелий» означает «солнечный». Спектральный анализ проводится не только с помощью спектра испускания, но и спектра поглощения.
Пример №4
Дано: 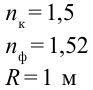
Формула:
Решение:
Дифракция волн и дифракция света
Световые лучи бывают параллельные, дивергентные (расходящиеся) и конвергентные (сходящиеся). Лучи, падающие на земную поверхность из источников, находящихся на очень больших расстояниях, например, от Солнца, звезд. Луны, принято считать параллельными.
Свет в вакууме и однородной среде распространяется прямолинейно.
Однородной называется среда, в которой её свойства по всему объёму одинаковы.
Образование тени является результатом прямолинейного распространения света.
Прогуливаясь на природе, вы возможно обращали внимание на паутину, искусно сплетенную пауками. Иногда она привлекает внимание, поблескивая всеми цветами радуги.
Волновая поверхность и фронт волны
Закономерности распространения любых волн в разных средах носят универсальный характер. Например, колебания, созданные в точке падения капли на неподвижной водной поверхности, распространяются с течением времени с одинаковой скоростью, охватывая определенную часть среды (b). С течением времени волна, продолжая распространяться, возмущает еще большую часть водной поверхности. Значит, в процессе распространения волны поверхность воды (среда) состоит из части, в которой волна распространилась, и части, в которой еще не распространилась. Линия, отделяющая эти части волны, называется волновой поверхностью.
Волновая поверхность — геометрическое место точек, до которых в данный момент времени дошла волна.
Определенный набор частиц среды, в которой распространяется волна, колеблется в одинаковой фазе. Поверхность, во всех точках которой колебания происходят в одинаковой фазе, называют поверхностью одинаковой фазы, или фронтом волны.
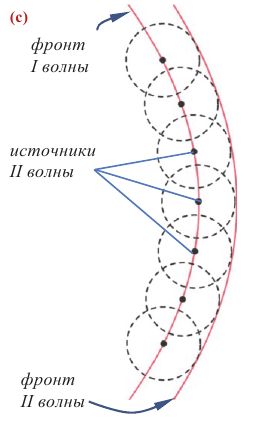
Фронт волны, являясь геометрической концепцией, создает представление о поверхности, проходящей через точки, колеблющиеся в одинаковых фазах (с). Значение фазы колебаний различных последовательных точек среды при распространении волны в ней может иметь различное значение, поэтому в этой среде может одновременно существовать бесконечное количество фронтов волны.
Волна, фронт которой представляет собой плоскость, называется плоской волной, а волну с фронтом сферической или цилиндрической формы называют соответственно сферической или цилиндрической волной.
Плоская волна распространяется в направлении, перпендикулярном плоскому фронту волны.
Дифракция волн и принцип Гюйгенса
Одним из общих свойств, присущих всем видам волн, является их дифракция.
Огибание волной препятствий связано с соотношением размера препятствия с длиной волны. Явление дифракции наблюдается при соблюдении соотношения:
Дифракцию можно объяснить на основе принципа, сформированного Гюйгенсом в 1690 году. Согласно принципу Гюйгенса, каждая точка среды, до которой доходит фронт волны, превращается в источник полусферических волн с частотой колебаний, равной частоте колебаний исходной волны. Касательная к этим сферическим волнам (их называют вторичными волнами) представляет собой новый фронт волны в следующий момент времени (см. с).
Принцип Гюйгенса-Френеля
• Дифракция света — явление отклонения от закона прямолинейного распространения света при прохождении вблизи препятствий и попадания в зону геометрической тени. Принцип Гюйгенса, дополненный Френелем принципом интерференции, называется принципом Гюйгенса-Френеля.
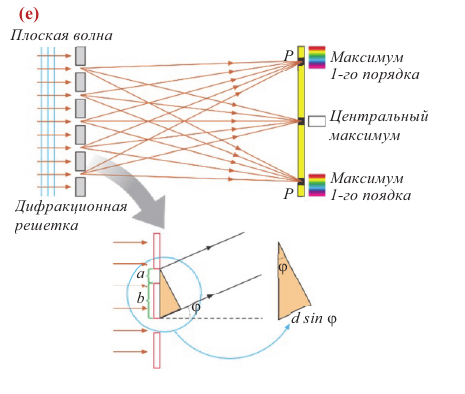
Этот (обобщенный) принцип позволил объяснить дифракцию количественно. Длина световой волны очень мала, поэтому дифракция света наблюдается при прохождении света сквозь щели очень малого размера или у края предметов. Поэтому для наблюдения и количественного исследования дифракции света используют специальное устройство, называемое дифракционной решеткой (е).
Дифракционная решетка — оптический прибор, разлагающий свет на спектр и позволяющий измерять длину световой волны.
Дифракционная решетка представляет собой совокупность большого числа непрозрачных штрихов, разделенных очень узкими прозрачными полосками (обычно на 1 мм прибора приходится от 500 до 1200 таких штрихов). Лучи света, падающие на дифракционную решетку перпендикулярно её поверхности, проходя сквозь прозрачные полоски, выходят отклоняющимися на некоторый угол (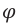
Условие максимума для дифракционной решетки будет иметь вид:
Все максимумы прошедшего через дифракционную решетку белого света (за исключением центрального, нулевого) получаются цветными. Начиная с центра, каждый максимум отражает 7 видимых цветов от фиолетового до красного. Это называют дифракционным спектром. В отличие от дисперсионного спектра полученные в дифракционном спектре более всего отклоняются красные лучи, менее всего отклоняются лучи фиолетового цвета.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.