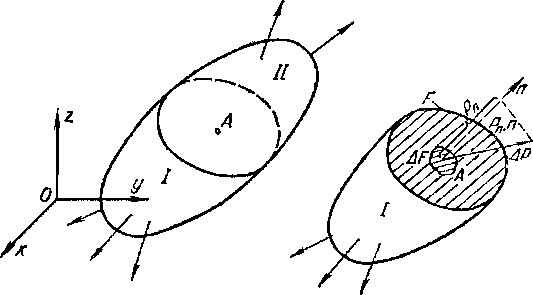в чем измеряется сопротивление материалов

Лекция 1. Сопротивление материалов. Основные понятия и определения

Основные определения

Сопротивление материалов позволяет определить прочность, жесткость и устойчивость элементов строительных конструкций и деталей машин, тем самым обеспечить долгую и надежную работу сооружений, машин и механизмов.

Вещества и комбинации веществ, из которых состоят тела, и являются рассматриваемыми материалами. Все твердые тела по геометрической форме можно условно разделить на 3 группы:

Это можно выразить соотношением длины к высоте или ширине. Стержни можно условно разделить на 3 категории:

1.1. Стержни с соотношением l/h ≥ 10.

Таким образом линия, изображающая стержень на чертежах, совпадает с осью стержня. Часто ось стержня называется упругой линией, нейтральной линией или нейтральной осью.

при которых исключается возможность разрушения конструкции при действии заданных нагрузок. Другими словами напряжения, возникающие в рассматриваемых поперечных сечениях, не должны превышать расчетного сопротивления материала.

возникающих под действием заданных нагрузок. Так как не существует материалов, имеющих бесконечно большую жесткость, то деформации материала конструкции приводят к изменению геометрической формы элементов конструкции, а значит и к перераспределению внутренних напряжений.

при котором изменение первоначальной геометрической формы под действием нагрузок и возникающего при этом перераспределения внутренних напряжений не приводит к разрушению конструкции.

Деформации рассматриваются как перемещение точек, линий и плоскостей.

Линейная деформация измеряется в единицах длины.

относительно некоторой точки.

на рассматриваемом участке длины элемента конструкции.

остающиеся после снятия нагрузки.

Другими словами остаточные деформации, при упругой деформации равны нулю.

после снятия нагрузок.

Все материалы обладают определенными упругими и пластичными свойствами. Например изготовление профилированного листа из листа металлопроката происходит в результате накопления остаточных деформаций.

Если силы направлены по оси, то такой элемент конструкции называют центрально сжатым или центрально растянутым. Если силы приложены на некотором расстоянии от оси, то такой элемент называют внецентренно сжатым или внецентренно растянутым, при этом расстояние от оси до точки приложения силы называется эксцентриситетом е.

т.е. в плоскости поперечного сечения

т.е. в плоскости, перпендикулярной плоскости поперечного сечения.

Моменты могут быть крутящими и изгибающими. Момент, возникающий при внецентренном растяжении или сжатии, является изгибающим.

К изотропным материалам условно можно отнести металлы, камень, стекло.

Представителем такого материала является древесина.

Свойства анизотропных материалов не являются предметом рассмотрения теории сопротивления материалов. Между тем не существует природных или искусственных материалов, имеющих идеальную упругость, изотропию или отротропию. Кроме того изготовить конструкцию идеальной геометрической формы практически невозможно. Это означает, что для точных расчетов необходимо учитывать все изменения геометрической формы, а также возможные отклонения от заданных физико-механических свойств. Однако в подавляющем большинстве случаев для обеспечения надежной работы строительной конструкции, машины или механизма достаточно выполнить приближенный (упрощенный) расчет. Выполняется такой расчет на основании следующих допущений.

Основные допущения, принимаемые в теории сопротивления материалов

1. Рассматриваемый материал является изотропным (или ортотропным) и идеально упругим.

2. Деформации материала пропорциональны приложенной нагрузке, не превышающей некоторой предельной величины, т.е рассматриваемые тела являются линейно-деформируемыми.

3. При составлении уравнений равновесия деформациями материала можно пренебречь, так как деформации рассматриваемых элементов значительно меньше геометрических размеров элементов. В данном случае не только значительно меньше длины, но также высоты и ширины.

4. При расчетах допускается использовать принцип независимости действия сил, т.е. упругую деформацию под действием нескольких сил можно рассматривать как сумму упругих деформаций от каждой отдельно взятой силы.

5. Предполагается, что сечения которые были плоскими до приложения нагрузок, остаются плоскими при деформациях материала.

Внешние и внутренние силы

Все силы, действующие на тело, можно условно разделить на внешние и внутренние. Условно потому, что силы тяжести, действующие на каждую частицу тела, находятся как бы внутри тела, а внутренние силы (силы взаимодействия между элементарными частицами вещества) действуют и до того, как к телу приложена какая-либо внешняя сила.

Внешние силы по характеру приложения можно разделить на четыре вида:

Так как при расчетах изначально рассматривается ось стержня, не имеющая высоты и ширины, то объемные и плоские нагрузки часто приводятся к линейной. Это допускается делать без каких-либо поправочных коэффициентов, если интенсивность объемной или плоской нагрузки является постоянной.

В природе точечных нагрузок не существует. Любая нагрузка прикладывается к некоторой площади, но если площадь приложения нагрузки, точнее длина приложения нагрузки после приведения плоской нагрузки к линейной, значительно меньше длины тела, то такую нагрузку можно условно рассматривать, как сосредоточенную в одной точке. Переход от сосредоточенной нагрузки к равномерно распределенной и наоборот осуществляется только с помощью соответствующих коэффициентов.

По времени действия нагрузки делятся на постоянные и временные

Постоянные нагрузки, например, собственный вес конструкции, действуют в течение всего срока службы. Временные нагрузки ограничены по времени действия.

По характеру изменения во времени нагрузки делятся на статические и динамические

Статические нагрузки прикладываются как бы постепенно, поэтому инертные силы, возникающие при движении инертных масс, при расчетах не учитываются. Динамические нагрузки прикладываются очень быстро и потому при расчетах влияние инертных сил необходимо учитывать.

Все вышеприведенные нагрузки рассматриваются как активные.

Равнодействующую внутренних сил, действующую на рассматриваемую площадь, называют внутренним усилием.

Уравнения равновесия. Метод сечений

Кроме того, если рассечь тело в любом месте, то чтобы тело по-прежнему оставалось в состоянии равновесия к полученному сечению нужно приложить некоторую внешнюю силу Q. Значение внешней силы определяется, исходя из условий равновесия. А так как сила действия равна силе противодействия, то считается, что внутренние усилия Р или напряжения р, возникающие в результате действия внешних сил (нагрузок) равны по значению нагрузкам, приложенным в рассматриваемом сечении и направлены в противоположную сторону. Такой метод расчета и называется методом сечений.

Примечание: Для решения статически неопределимых задач одних только уравнений равновесия и уравнения моментов недостаточно.

Рисунок 317.1

Так как напряжения, возникающие в рассматриваемых сечениях под действием внешних сил, редко бывают равномерно распределенными (не имеют постоянной интенсивности), то для решения задач сопротивления материалов важно знать не просто значение внутренних усилий, но также и значение напряжений в наиболее опасных точках сечения. Отношение внутреннего усилия ΔР, действующего на некоторой площади ΔF рассматриваемого сечения будет приближаться к некоторому пределу, если площадь ΔF будет стремиться к нулю (к точке А). Этот предел, как мы выяснили ранее, называется напряжением и определяет интенсивность внутренних усилий, действующих на рассматриваемую площадку в точке А. Напряжения могут быть различны не только в разных точках одного сечения, но и в одной и той же точке А, общей для различных сечений, т.е. сечений, рассекающих тело под различными углами.

Ось, перпендикулярная плоскости сечения, называется нормалью.

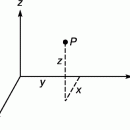
Полное напряжение в точке А, имеющей координаты (х, у, z) для сечения с нормалью n определяется по формуле:

(317.1)

где ΔР — элементарное внутреннее усилие, возникающее при отбрасывании части II тела и замене этой части элементарной внешней силой ΔQ, действующей на оставшуюся часть I для соблюдения условий равновесия.

Нормальное напряжение σ_n действует в направлении нормали

Если усилие ΔР не перпендикулярно рассматриваемой плоскости сечения (как на рисунке 317.1), то значение нормального напряжения можно определить по формуле:

(317.2)

Касательное напряжение т_n действует в плоскости сечения

Значение касательного напряжения можно определить по формуле:

(317.3)

дальше

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

Сопротивление материалов

Сопротивление материалов (в обиходе — сопромат) — часть механики деформируемого твёрдого тела, которая рассматривает методы инженерных расчётов конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности, экономичности и долговечности. Сопротивление материалов относится к фундаментальным дисциплинам общеинженерной подготовки специалистов с высшим техническим образованием, за исключением специальностей, не связанных с проектированием объектов, для которых прочность является важным показателем.

Содержание

Определение

Сопротивление материалов базируется на понятии «прочность», что является способностью материала противостоять приложенным нагрузкам и воздействиям без разрушения. Сопротивление материалов оперирует такими понятиями как: внутренние усилия, напряжения, деформации. Приложенная внешняя нагрузка к некоторому телу порождает внутренние усилия в нём, противодействующие активному действию внешней нагрузки. Внутренние усилия, распределенные по сечениям тела называются напряжениями. Таким образом, внешняя нагрузка порождает внутреннюю реакцию материала, характеризующуюся напряжениями,которые в свою очередь прямо пропорциональны деформациям тела. Деформации бывают линейные такие как удлинение,укорочение, сдвиг и углы поворота сечений. Основные понятия сопротивления материалов оценивающие способность материала сопротивляться внешним воздействиям являются:

Связь с другими науками

В теоретической части сопротивление материалов базируется на математике и теоретической механике, в экспериментальной части — на физике и материаловедении и применяется при проектировании машин, приборов и конструкций. Практически все специальные дисциплины подготовки инженеров по разным специальностям содержат разделы курса сопротивления материалов, так как создание работоспособной новой техники невозможно без анализа и расчета её прочности, жёсткости и надёжности.

Задачей сопротивления материалов, как одного из разделов механики сплошной среды, является определение деформаций и напряжений в твёрдом упругом теле, которое подвергается силовому или тепловому воздействию.

Эта же задача среди других рассматривается в курсе теории упругости. Однако методы решения этой общей задачи в том и другом курсах существенно отличаются друг от друга. Сопротивление материалов решает её главным образом для бруса, базируясь на ряде гипотез геометрического или физического характера. Такой метод позволяет получить, хотя и не во всех случаях, вполне точные, но достаточно простые формулы для вычисления напряжений. Также поведением деформируемых твёрдых тел под нагрузкой занимается теория пластичности и теория вязкоупругости.

Гипотезы и допущения

Расчет конструкций и их элементов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов существует модель идеализированного деформируемого тела.

Эти положения ограниченно применимы к решению конкретных закдач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда.

Теории прочности

Прочность конструкций определяется с использованием теории разрушения — науки о прогнозировании условий, при которых твердые материалы разрушаются под действием внешних нагрузок. Материалы, как правило, подразделяются на разрушающиеся хрупко и пластично. В зависимости от условий (например, температура, состояние напряжений, виды нагрузки) большинство материалов может быть отнесено к хрупким или пластичным или обоим видам одновременно. Тем не менее, для большинства практических ситуаций, материалы могут быть классифицированы как хрупкие или пластичные. Несмотря на то, что теория разрушения находится в разработке уже более 200 лет, уровень её приемлемости для механики сплошных сред, не всегда достаточен.

В математических терминах, теория разрушения выражается в виде различных критериев разрушения, которые справедливы для конкретных материалов. Критерием разрушения является поверхность разрушения, выраженная через напряжения или деформации. Поверхность разрушения разделяет «поврежденное» и «не поврежденное» состояния. Для «поврежденного» состояния трудно дать точное физическое определение. Поэтому это понятие следует рассматривать как рабочее определение, используемое в инженерном сообществе. Термин «поверхность разрушения», используемый в теории прочности, не следует путать с аналогичным термином, который определяет физическую границу между поврежденными и не поврежденными частями тела. Довольно часто феноменологические критерии разрушения одного и того же вида используются для прогнозирования хрупкого и пластичного разрушения.

Среди феноменологических теорий прочности наиболее известными являются следующие теории, которые принято называть «классическими» теориями прочности:

1. Теория наибольших нормальных напряжений.

2. Теория наибольших деформаций.

3. Теория наибольших касательных напряжений Треска (Tresca).

4. Теория наибольшей удельной потенциальной энергии формоизменения фон Мизеса (von Mises).

Классические теории прочности имеют существенные ограничения для их применения. Так теории наибольших нормальных напряжений и наибольших деформаций применимы лишь для расчета прочности хрупких материалов, причём только для некоторых определённых условий нагружения. Поэтому эти теории прочности сегодня применяют весьма ограниченно. Из перечисленных теорий наиболее часто используют теорию Мора, которую также называют критерием Мора-Кулона. Кулон (Coulomb) в 1781 г. на основе выполненных им испытаний установил закон сухого трения, который использовал для расчета устойчивости подпорных стенок. Математическая формулировка закона Кулона совпадает с теорией Мора, если в ней выразить главные напряжения через касательные и нормальные напряжения на площадке среза. Достоинством теории Мора является то, что она применима к материалам, имеющим разные сопротивления сжатию и растяжению, а недостатком то, что она учитывает влияние только двух главных напряжений — максимального и минимального. Поэтому теория Мора не точно оценивает прочность при трехосном напряженном состоянии, когда необходимо учитывать все три главных напряжения. Кроме того, при использовании эта теория не учитывается поперечное расширение (дилатацию) материала при сдвиге. На эти недостатки теории Мора неоднократно обращал внимание А. А. Гвоздев, который доказал неприменимость теории Мора для бетона [2].

На смену «классическим» теориям прочности в современной практике пришли многочисленные новые новые теории разрушения. Большинство из них используют различные комбинации инвариантов тензора напряжений Коши (Cauchy) Среди них наиболее известны следующие критерии разрушения:

Перечисленные критерии прочности предназначены для расчета прочности однородных (гомогенных) материалов. Некоторые из них используются для расчёта анизотропных материалов.

Для расчета прочности неоднородных (не гомогенных) материалов используется два подхода, называемые макро-моделированием и микро-моделированием. Оба подхода ориентированы на использование метода конечных элементов и вычислительной техники. При макро-моделировании предварительно выполняется гомогенизация — условная замена неоднородного (гетерогенного) материала на однородный (гомогенный). При микро-моделировании компоненты материала рассматриваются с учётом их физических характеристик. Микро-моделирование используют в основном в исследовательских целях, так как расчет реальных конструкций требует чрезмерно больших затрат машинного времени. Методы гомогенизации широко используются для расчета прочности каменных конструкций, в первую очередь для расчета стен-диафрагм жесткости зданий. Критерии разрушения каменных конструкций учитывают многообразные формы разрушения каменной кладки. Поэтому поверхность разрушения, как правило. принимается в виде нескольких пересекающихся поверхностей, которые могут иметь разную геометрическую форму.

Применение

Методы сопротивления материалов широко используются при расчете несущих конструкций зданий и сооружений, в дисциплинах связанных с проектированием деталей машин и механизмов.

Как правило, именно из-за оценочного характера результатов, получаемых с помощью математических моделей этой дисциплины, при проектировании реальных конструкций все прочностные характеристики материалов и изделий выбираются с существенным запасом (в несколько раз относительно результата, полученного при расчетах).

В студенческой среде сопротивление материалов считается одной из наиболее сложных общепрофессиональных дисциплин, что дало богатую пищу студенческому фольклору и породило целый ряд шуток и анекдотов.

См. также

Литература

Источник

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ, раздел механики твердого тела, изучающий напряжения и деформации, которые обусловлены силами, действующими на твердые тела – элементы конструкции. Эту дисциплину можно характеризовать и как науку о методах расчета элементов конструкции на прочность, жесткость и устойчивость.

Напряжение, создаваемое в твердом теле внешними нагрузками, есть мера (с размерностью силы на единицу площади) интенсивности внутренних сил, действующих со стороны одной, мысленно отсекаемой, части тела на другую, оставшуюся (метод сечений). Внешние нагрузки вызывают деформацию тела, т.е. изменение его размеров и формы. В сопротивлении материалов исследуются соотношения между нагрузками, напряжениями и деформациями, причем исследования ведутся, с одной стороны, путем математического вывода формул, связывающих нагрузки с вызываемыми ими напряжениями и деформациями, а с другой – путем экспериментального определения характеристик материалов, применяемых в строениях и машинах. См. также МЕТАЛЛОВ МЕХАНИЧЕСКИЕ СВОЙСТВА; МЕТАЛЛОВ ИСПЫТАНИЯ. По найденным формулам с учетом результатов испытания материалов рассчитываются размеры элементов строений и машин, обеспечивающие сопротивление заданным нагрузкам. Сопротивление материалов не относится к точным наукам, так как многие его формулы выводятся на основе предположений о поведении материалов, которые не всегда точно выполняются. Тем не менее, пользуясь ими, грамотный инженер может создавать надежные и экономичные конструкции.

С сопротивлением материалов тесно связана математическая теория упругости, в которой тоже рассматриваются напряжения и деформации. Она позволяет решать те задачи, которые с трудом поддаются решению обычными методами сопротивления материалов. Однако между сопротивлением материалов и теорией упругости нет четкой границы. Хотя почти все задачи о распределении напряжений решены методами математического анализа, при сложных условиях эти решения требуют трудоемких выкладок. И тогда на помощь приходят экспериментальные методы анализа напряжений.

НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ

Виды напряжений.

Самое важное понятие в сопротивлении материалов – это понятие напряжения как силы, действующей на малую площадку и отнесенной к площади этой площадки. Напряжения бывают трех видов: растяжения, сжатия и сдвига.

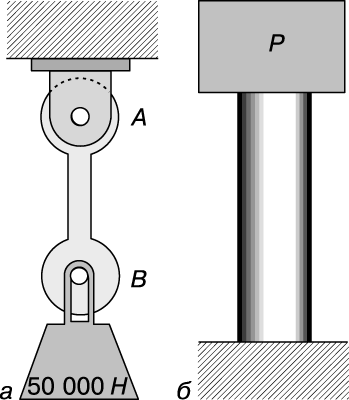
Рассмотрим короткий цилиндр (рис. 1,б), на верхний торец которого положен груз. При этом во всех поперечных сечениях цилиндра действуют напряжения сжатия. Если напряжение равномерно распределено по всему сечению, то справедлива формула S = P/A. Сжатый цилиндр короче, чем в отсутствие деформаций.

Напряжения растяжения и сжатия направлены по нормали (т.е. вдоль перпендикуляра) к площадке, в которой они действуют, а напряжение сдвига – параллельно площадке. Поэтому напряжения растяжения и сжатия называются нормальными, а напряжения сдвига – касательными.

Деформация.

Деформацией называется изменение размера тела под действием приложенных к нему нагрузок. Деформация, отнесенная к полному размеру, называется относительной. Если изменение каждого малого элемента длины тела одинаково, то относительная деформация называется равномерной. Относительную деформацию часто обозначают символом d, а полную – символом D. Если относительная деформация постоянна по всей длине L, то d = D/L. Например, если длина стального стержня до приложения растягивающей нагрузки равна 2,00 м, а после нагружения – 2,0015 м, то полная деформация D равна 0,0015 м, а относительная – d = 0,0015/2,00 = 0,00075 (м/м).

Почти для всех материалов, применяемых в строениях и машинах, относительная деформация пропорциональна напряжению, пока оно не превысит т.н. предела пропорциональности. Это очень важное соотношение называется законом Гука. Оно было экспериментально установлено и сформулировано в 1678 английским изобретателем и часовых дел мастером Р.Гуком. Данное соотношение между напряжением и деформацией для любого материала выражается формулой S = Ed, где E – постоянный множитель, характеризующий материал. Этот множитель называют модулем Юнга по имени Т.Юнга, который ввел его в 1802, или же модулем упругости. Из обычных конструкционных материалов наибольший модуль упругости у стали; он равен примерно 200 000 МПа. В стальном стержне относительная деформация, равная 0,00075, из приводившегося ранее примера вызывается напряжением S = Ed = 200 000 ґ 0,00075 = 150 МПа, что меньше предела пропорциональности конструкционной стали. Если бы стержень был из алюминия с модулем упругости около 70 000 МПа, то, чтобы вызвать ту же самую деформацию 0,00075, достаточно было бы напряжения немногим более 50 МПа. Из сказанного ясно, что упругие деформации в строениях и машинах очень малы. Даже при сравнительно большом напряжении 150 МПа из приведенного выше примера относительная деформация стального стержня не превышает одной тысячной. Столь большая жесткость стали – ее ценное качество.

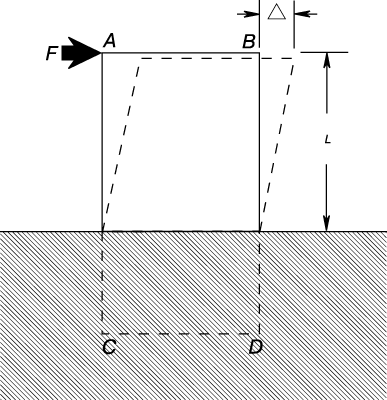
Чтобы наглядно представить деформацию сдвига, рассмотрим, например, прямоугольную призму ABCD (рис. 3). Ее нижний конец жестко заделан в твердое основание. Если на верхнюю часть призмы действует горизонтальная внешняя сила F, она вызывает деформацию сдвига, показанную штриховыми линиями. Смещение D есть полная деформация на длине (высоте) L. Относительная деформация сдвига d равна D/L. Для деформации сдвига тоже выполняется закон Гука при условии, что напряжение не превышает предела пропорциональности для сдвига. Следовательно, S_s = E_sd, где E_s – модуль сдвига. Для любого материала величина E_s меньше E. Для стали она составляет около 2/5 E, т.е. приблизительно 80 000 МПа. Важный случай деформации сдвига – деформация в валах, на которые действуют внешние скручивающие моменты.

Выше речь шла об упругих деформациях, которые вызываются напряжениями, не превышающими предела пропорциональности. Если же напряжение выходит за предел пропорциональности, то деформация начинает расти быстрее, чем напряжение. Закон Гука перестает быть справедливым. В случае конструкционной стали в области, лежащей чуть выше предела пропорциональности, небольшое увеличение напряжения приводит к увеличению деформации во много раз по сравнению с деформацией, соответствующей пределу пропорциональности. Напряжение, при котором начинается столь быстрый рост деформации, называется пределом текучести. Материал, в котором разрушению предшествует большая неупругая деформация, называется пластичным.

ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ

Допускаемое (допустимое) напряжение – это значение напряжения, которое считается предельно приемлемым при вычислении размеров поперечного сечения элемента, рассчитываемого на заданную нагрузку. Можно говорить о допускаемых напряжениях растяжения, сжатия и сдвига. Допускаемые напряжения либо предписываются компетентной инстанцией (скажем, отделом мостов управления железной дороги), либо выбираются конструктором, хорошо знающим свойства материала и условия его применения. Допускаемым напряжением ограничивается максимальное рабочее напряжение конструкции.

При проектировании конструкций ставится цель создать конструкцию, которая, будучи надежной, в то же время была бы предельно легкой и экономной. Надежность обеспечивается тем, что каждому элементу придают такие размеры, при которых максимальное рабочее напряжение в нем будет в определенной степени меньше напряжения, вызывающего потерю прочности этим элементом. Потеря прочности не обязательно означает разрушение. Машина или строительная конструкция считается отказавшей, когда она не может удовлетворительно выполнять свою функцию. Деталь из пластичного материала, как правило, теряет прочность, когда напряжение в ней достигает предела текучести, так как при этом из-за слишком большой деформации детали машина или конструкция перестает соответствовать своему назначению. Если же деталь выполнена из хрупкого материала, то она почти не деформируется, и потеря ею прочности совпадает с ее разрушением.

Запас прочности.

Разность напряжения, при котором материал теряет прочность, и допускаемого напряжения есть тот «запас прочности», который необходимо предусматривать, учитывая возможность случайной перегрузки, неточностей расчета, связанных с упрощающими предположениями и неопределенными условиями, наличия не обнаруженных (или не обнаружимых) дефектов материала и последующего снижения прочности из-за коррозии металла, гниения дерева и пр.

Коэффициент запаса.

Коэффициент запаса прочности какого-либо элемента конструкции равен отношению предельной нагрузки, вызывающей потерю прочности элемента, к нагрузке, создающей допускаемое напряжение. При этом под потерей прочности понимается не только разрушение элемента, но и появление в нем остаточных деформаций. Поэтому для элемента конструкции, выполненного из пластичного материала, предельным напряжением является предел текучести. В большинстве случаев рабочие напряжения в элементах конструкции пропорциональны нагрузкам, а поэтому коэффициент запаса определяется как отношение предела прочности к допускаемому напряжению (коэффициент запаса по пределу прочности). Так, если предел прочности конструкционной стали равен 540 МПа, а допускаемое напряжение – 180 МПа, то коэффициент запаса равен 3.

РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ

В сопротивлении материалов большое внимание уделяется выводу соотношений между заданными нагрузками, размерами и формой элемента конструкции, несущего эти нагрузки или сопротивляющегося им, и напряжениями, возникающими в определенных сечениях элемента конструкции. Как правило, цель расчетов состоит в том, чтобы найти необходимые размеры элемента, при которых максимальное рабочее напряжение в нем не будет превышать допускаемого.

В элементарном курсе сопротивления материалов рассматривается ряд типичных случаев равномерного распределения напряжений: растянутые стержни, короткие сжатые стержни, тонкостенные цилиндры, работающие под давлением внутренней среды (котлы и резервуары), заклепочные и сварные соединения, температурные напряжения и такие статически неопределимые системы, как растянутые стержни из нескольких разных материалов.

Если напряжение одинаково во всех точках поперечного сечения, то S = P/A. Конструктор находит необходимую площадь поперечного сечения, поделив заданную нагрузку на допускаемое напряжение. Но нужно уметь отличать случаи, в которых напряжение действительно распределено равномерно, от других, сходных случаев, в которых этого нет. Необходимо также (как в задаче о заклепочных соединениях, в которых существуют напряжения и растяжения, и сжатия, и сдвига) находить плоскости, в которых действуют напряжения разного вида, и определять максимальные местные напряжения.

Тонкостенный цилиндр.

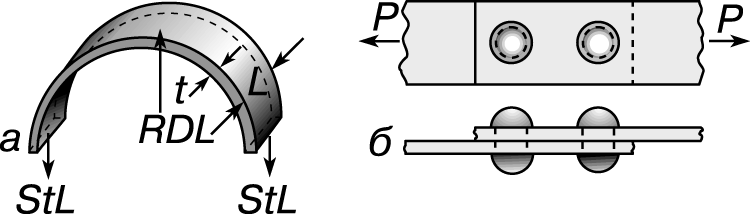
Такой резервуар выходит из строя (разрывается), когда напряжение растяжения в его оболочке становится равным пределу прочности материала. Формулу, связывающую толщину стенки t, внутренний диаметр резервуара D, напряжение S и внутреннее давление R, можно вывести, рассмотрев условия равновесия кольца, вырезанного из его оболочки двумя поперечными плоскостями, разделенными расстоянием L (рис. 4,а). Внутреннее давление действует на внутреннюю поверхность полукольца с направленной вверх силой, равной произведению RDL, а напряжения в двух горизонтальных концевых сечениях полукольца создают две направленные вниз силы, каждая из которых равна tLS. Приравнивая, получаем

Заклепочное соединение.

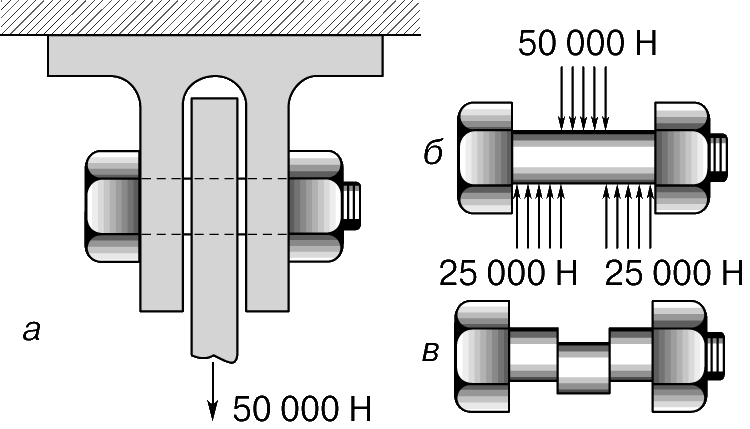
На рис. 4,б представлено двухзаклепочное соединение двух полос внахлестку. Такое соединение может выйти из строя из-за перерезывания обеих заклепок, разрыва одной из полос в том месте, где она ослаблена отверстием под заклепку, или из-за слишком больших напряжений смятия по площади соприкосновения заклепки с полосой. Напряжение смятия в заклепочном соединении вычисляется как нагрузка на одну заклепку, деленная на диаметр заклепки и на толщину полосы. Допускаемой для такого соединения принимается наименьшая из нагрузок, соответствующих допускаемым напряжениям трех указанных видов.

Вообще говоря, напряжение, действующее в поперечном сечении растянутого или короткого сжатого стержня, можно с полным основанием считать равномерно распределенным, если равные и противоположно направленные нагрузки приложены так, что равнодействующая каждой из них проходит через центр тяжести рассматриваемого поперечного сечения. Но нужно иметь в виду, что ряд задач (и к ним относится задача о напряжениях смятия в заклепочном соединении) решается в предположении о равномерном распределении напряжения, хотя это заведомо не соответствует действительности. Допустимость такого подхода проверяется опытным путем.

НЕРАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ

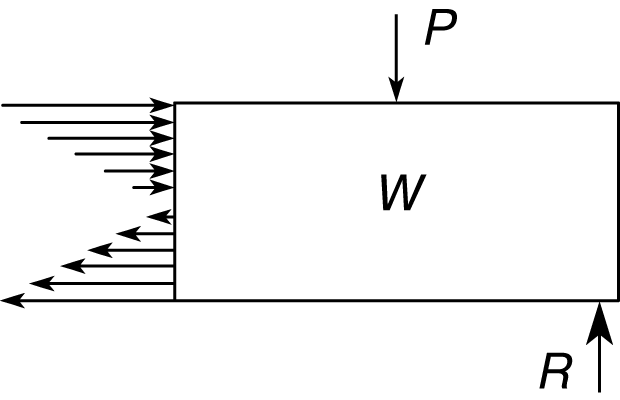
Многие элементы строений и детали машин нагружаются так, что напряжения во всех их поперечных сечениях распределены неравномерно. Чтобы вывести формулы для расчета напряжений в таких условиях, мысленно разрезают элемент плоскостью, которая дает нужное поперечное сечение, на две части и рассматривают условия равновесия одной из них. На эту часть действуют одна или несколько заданных внешних сил, а также силы, эквивалентные напряжениям в данном поперечном сечении. Действующие напряжения должны удовлетворять условиям равновесия и соответствовать деформациям. Эти два требования составляют основу для решения задачи. Второе из них подразумевает справедливость закона Гука. Типичными элементами с неравномерным распределением напряжений являются нагруженные балки, валы под действием скручивающих сил, растянутые или сжатые стержни с дополнительным изгибом и колонны.

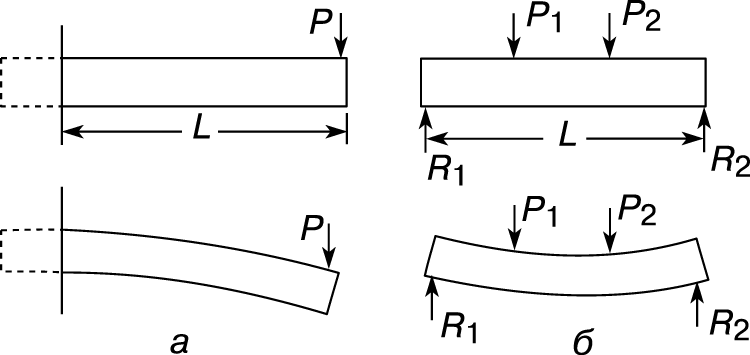
БАЛКИ.

Балка – это длинный стержень с опорами и нагрузками, работающий в основном на изгиб. Поперечное сечение балки обычно одинаково по всей ее длине. Силы, с которыми опоры действуют на балку, называются реакциями опор. Наиболее распространены два вида балок: консольная (рис. 5,а) и балка с двумя опорами, называемая простой (рис. 5,б). Под действием нагрузок балка прогибается. При этом «волокна» на ее верхней стороне сокращаются, а на нижней – удлиняются. Очевидно, что где-то между верхней и нижней сторонами балки имеется тонкий слой, длина которого не изменяется. Он называется нейтральным слоем. Изменение длины волокна, расположенного между верхней (или нижней) стороной балки и ее нейтральным слоем, пропорционально расстоянию до нейтрального слоя. Если справедлив закон Гука, то напряжения тоже пропорциональны этому расстоянию.

Формула изгиба.

На основе указанного распределения напряжений, дополненного условиями статики, выведена т.н. формула изгиба, в которой напряжение выражается через нагрузки и размеры балки. Она обычно представляется в виде S = Mc/I, где S – максимальное напряжение в рассматриваемом поперечном сечении, c – расстояние от нейтрального слоя до наиболее напряженного волокна, M – изгибающий момент, равный сумме моментов всех сил, действующих по одну сторону от этого сечения, а I – момент инерции поперечного сечения (определенная функция формы и размеров последнего). Характер изменения нормальных напряжений в поперечном сечении балки показан на рис. 6.

В поперечных сечениях балок действуют также касательные напряжения. Их вызывает равнодействующая всех вертикальных сил, приложенных по одну сторону поперечного сечения горизонтальной балки. Сумма всех внешних сил и реакций, действующих на одну из двух частей балки, называется сдвигом в сечении балки и обычно обозначается через V. Касательные напряжения неравномерно распределены по сечению: они равны нулю на верхнем и нижнем краях сечения и почти всегда максимальны в нейтральном слое.

Прогиб балки.

Часто требуется рассчитать прогиб балки, вызванный действием нагрузки, т.е. вертикальное смещение точки, лежащей в нейтральном слое. Это очень важная задача, поскольку прогиб и кривизну балки нужно знать при решении задач, относящихся к широкому кругу т.н. статически неопределимых систем.

Еще в 1757 Л.Эйлер вывел формулу для кривизны изогнутой балки. В этой формуле кривизна балки выражается через переменный изгибающий момент. Чтобы найти ординату упругой кривой (прогиб), необходимо брать двойной интеграл. В 1868 О.Мор (Германия) предложил метод, основанный на эпюрах изгибающих моментов. Этот графоаналитический метод имеет огромное преимущество перед прежними методами, так как позволяет свести все математические вычисления к сравнительно простым арифметическим выкладкам. Он дает возможность вычислять прогиб и наклон в любой точке балки при любой нагрузке.

Статически неопределимые балки.

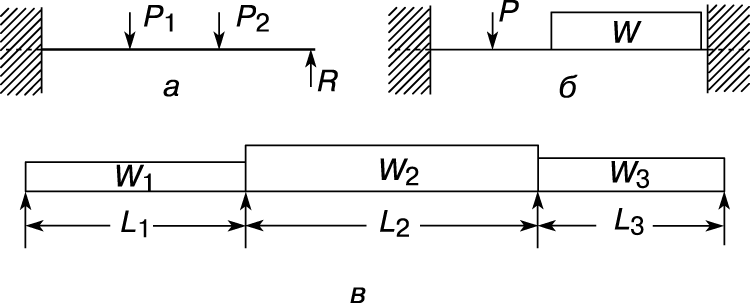
Многие балки, используемые в строениях и машинах, имеют более двух опор или только две опоры, но с заделкой одного из концов, исключающей возможность поворота. Такие балки называются статически неопределимыми, поскольку уравнений статики недостаточно для определения реакций в опорах и моментов в заделке. Чаще всего рассматриваются подобные балки трех типов: с одним заделанным (защемленным) концом и одной опорой, с заделанными обоими концами и неразрезные балки, имеющие более двух опор (рис. 7).

Первое решение задачи о неразрезных балках было опубликовано французским инженером Б.Клапейроном в 1857. Он доказал т.н. теорему о трех моментах. Уравнение трех моментов представляет собой соотношение между изгибающими моментами в трех последовательных опорах одной неразрезной балки. Например, в случае неразрезной балки с равномерной нагрузкой на каждом пролете это уравнение имеет вид

Здесь M_A, M_B и M_C – изгибающие моменты в трех опорах, L₁ и L₂ – длины левого и правого пролетов, W₁ – нагрузка на левый пролет, а W₂ – нагрузка на правый пролет. Нужно написать такое уравнение для каждой пары смежных пролетов, а затем решить полученную систему уравнений. Если число пролетов равно n, то число уравнений будет равно n – 1.

В 1930 Х.Кросс опубликовал свой метод расчета широкого круга статически неопределимых рам и неразрезных балок. Его «метод распределения моментов» позволяет обходиться без решения систем уравнений, сводя все вычисления к сложению и вычитанию чисел.

НАПРЯЖЕНИЕ ПРИ КРУЧЕНИИ.

Если к концам вала приложены равные, но противоположно направленные внешние скручивающие моменты, то во всех его поперечных сечениях существуют только касательные напряжения, т.е. напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг. В круговом поперечном сечении вала деформации сдвига и касательные напряжения равны нулю в центре и максимальны на краю; в промежуточных точках они пропорциональны расстоянию от центра тяжести сечения. Обычная формула для максимального касательного напряжения при кручении такова: S = Tc/J, где T – скручивающий момент на одном конце, c – радиус вала и J – полярный момент сечения. Для круга J = pr 4 /2. Эта формула применима только в случае кругового поперечного сечения. Формулы для валов с поперечным сечением другой формы выводятся путем решения соответствующих задач методами математической теории упругости с привлечением в некоторых случаях методов экспериментального анализа.

СЛОЖНОЕ СОПРОТИВЛЕНИЕ.

Нередко приходится рассчитывать балки, на которые в дополнение к поперечным нагрузкам действуют продольные силы растяжения или сжатия, приложенные к концам. В таких случаях напряжение в любой точке поперечного сечения равно алгебраической сумме нормального напряжения, создаваемого продольной нагрузкой, и изгибного напряжения, создаваемого поперечными нагрузками. Общая формула для напряжения в случае совместного действия изгиба и растяжения-сжатия такова: S = ± (P/A) ± (Mc/I), где знак «плюс» относится к растягивающему напряжению.

КОЛОННЫ.

Каркасы зданий и фермы мостов состоят в основном из растянутых стержней, балок и колонн. Колонны – это длинные сжатые стержни, примером которых в каркасах зданий могут служить вертикальные стержни, несущие межэтажные перекрытия.

Если длина сжатого стержня более чем в 10–15 раз превышает его толщину, то под действием критических нагрузок, приложенных к его концам, он, потеряв устойчивость, изогнется, даже если нагрузки номинально приложены по его оси (продольный изгиб). Вследствие такого изгиба нагрузка оказывается внецентренной. Если эксцентриситет в среднем поперечном сечении колонны равен D, то максимальное сжимающее напряжение в колонне будет равно (P/A) + (PDc/I). Отсюда видно, что допускаемая нагрузка для колонны должна быть меньше, чем для короткого сжатого стержня.

В строениях часто встречаются внецентренно нагруженные колонны. В результате точного теоретического анализа таких колонн были получены «формулы секанса». Но расчеты по этим формулам весьма трудоемки, а потому часто приходится прибегать к эмпирическим методам, дающим хорошие результаты.

СЛОЖНЫЕ НАПРЯЖЕННЫЕ СОСТОЯНИЯ

Напряжение в какой-либо точке той или иной плоскости нагруженного тела, вычисленное по обычным формулам, не обязательно будет наибольшим в этой точке. Поэтому важное значение имеет вопрос о соотношениях между напряжениями в разных плоскостях, проходящих через одну точку. Такие соотношения являются предметом раздела механики, посвященного сложным напряженным состояниям.

Соотношения между напряжениями.

Напряженное состояние в некоторой точке любого нагруженного тела можно полностью охарактеризовать, представив напряжения, действующие на грани элементарного куба в этой точке. Часто встречаются случаи, к которым относятся и рассмотренные выше, двухосного (плоского) напряженного состояния с напряжениями, равными нулю, на двух противоположных гранях куба. Напряжения, существующие в точке тела, неодинаковы в плоскостях с разным наклоном. Исходя из основных положений статики, можно сделать ряд важных выводов о соотношении между напряжениями в разных плоскостях. Приведем три из них:

1. Если в некоторой точке заданной плоскости имеется касательное напряжение, то точно такое же напряжение имеется в проходящей через эту точку плоскости, перпендикулярной заданной.

2. Существует плоскость, в которой нормальное напряжение больше, чем в любой другой.

3. В плоскости, перпендикулярной этой плоскости, нормальное напряжение меньше, чем в какой-либо другой.

Максимальное и минимальное нормальные напряжения, о которых говорится в п. 2 и 3, называются главными напряжениями, а соответствующие плоскости – главными плоскостями.

Необходимость в анализе главных напряжений на основе указанных соотношений не всегда возникает, так как простые формулы, которыми обычно пользуются инженеры, в большинстве случаев дают именно максимальные напряжения. Но в некоторых случаях, например при расчете вала, сопротивляющегося одновременно скручивающему и изгибающему моментам, нельзя обойтись без соотношений для сложного напряженного состояния.

БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ

В задачах, о которых говорилось выше, рассматривались напряжения либо равномерно распределенные, либо линейно меняющиеся с удалением от нейтральной оси, где напряжение равно нулю. Однако во многих случаях закон изменения напряжения более сложен.

В качестве примера задач с нелинейным распределением напряжений можно привести искривленные балки, толстостенные сосуды, работающие под высоким внутренним или наружным давлением, валы некругового поперечного сечения и нагруженные тела с резкими изменениями поперечного сечения (канавками, буртиками и т.д.). Для таких задач рассчитываются коэффициенты концентрации напряжений.

Кроме того, выше речь шла только о статических нагрузках, постепенно прилагаемых и снимаемых. Переменные же и периодически меняющиеся нагрузки, многократно повторенные, могут приводить к потере прочности, даже если они не превышают статического предела прочности рассматриваемого материала. Такие отказы называются усталостными, а проблема их предотвращения приобрела важное значение в наш век машин и механизмов, работающих на необычайно высоких скоростях. См. также СТАТИКА; ПРОЧНОСТНОЙ РАСЧЕТ КОНСТРУКЦИЙ; КОНСТРУКЦИОННЫЕ И СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ.

Беляев Н.М. Сопротивление материалов. М., 1978
Павлов П.А. Механические состояния и прочность материалов. Л., 1980
Биргер И.А., Мавлютов Р.Р. Сопротивление материалов. М., 1986
Писаренко Г.С. и др. Сопротивление материалов. Киев, 1986
Степин П.А. Сопротивление материалов. М., 1988
Бородин Н.А. Сопротивление материалов. М., 1992

Источник