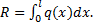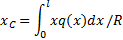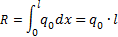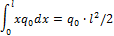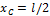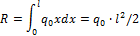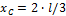в чем измеряется распределенная нагрузка

Понятие о распределенной нагрузке.

Наряду с рассмотренными выше сосредоточенными силами строительные конструкции и сооружения могут подвергаться воздействию распределенных нагрузок – по объему, по поверхности или вдоль некоторой линии – и определяемых ее интенсивностью.

Примером нагрузки, распределенной по площади, является снеговая нагрузка, давление ветра, жидкости или грунта. Интенсивность такой поверхностной нагрузки имеет размерность давления и измеряется в кН/м 2 или килопаскалях (кПа = кН/м 2 ).

При решении задач очень часто встречается нагрузка, распределенная по длине балки. Интенсивность q такой нагрузки измеряется в кН/м.

Рассмотрим балку, загруженную на участке [a, b] распределенной нагрузкой, интенсивность которой изменяется по закону q= q(x). Для определения опорных реакций такой балки нужно заменить распределенную нагрузку эквивалентной сосредоточенной. Это можно сделать по следующему правилу:

Рассмотрим частные случаи распределенной нагрузки.

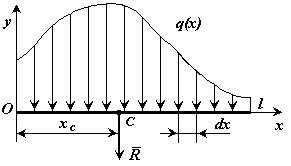
а) общий случай распределенной нагрузки (рис.24)

Рис.24

— элементарная сила.

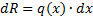
Распределенная по отрезку прямой сила интенсивности q(x) эквивалентна сосредоточенной силе

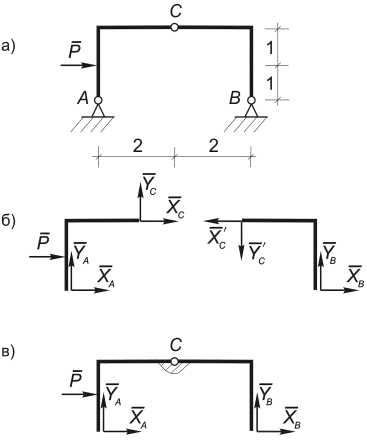
Сосредоточенная сила прикладывается в точке С (центре параллельных сил) с координатой

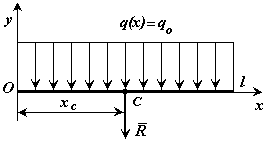
б) постоянная интенсивность распределенной нагрузки (рис.25)

Рис. 25

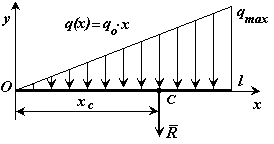
в) интенсивность распределенной нагрузки, меняющаяся по линейному закону (рис.26)

Рис. 26

Расчет составных систем.

Под составными системами будем понимать конструкции, состоящие из нескольких тел, соединенных друг с другом.

Прежде, чем переходить к рассмотрению особенностей расчета таких систем, введем следующее определение.

Статически определимыми называются такие задачи и системы статики, для которых число неизвестных реакций связей не превышает максимально допустимого числа уравнений.

Если число неизвестных больше числа уравнений, соответствующие задачи и системы называются статически неопределимыми. При этом разность между числом неизвестных и числом уравнений называется степенью статической неопределимости системы.

Для любой плоской системы сил, действующих на твердое тело, имеется три независимых условия равновесия. Следовательно, для любой плоской системы сил из условий равновесия можно найти не более трех неизвестных реакций связи.

В случае пространственной системы сил, действующих на твердое тело, имеется шесть независимых условия равновесия. Следовательно, для любой пространственной системы сил из условий равновесия можно найти не более шести неизвестных реакций связи.

Поясним это на следующих примерах.

1. Пусть центр невесомого идеального блока (пример 4) удерживается при помощи не двух, а трех стержней: АВ, ВС и BD и нужно определить реакции стержней, пренебрегая размерами блока.

С учетом условий задачи мы получим систему сходящихся сил, где для определения трех неизвестных: S_A, S_C и S_D можно составить по-прежнему систему только двух уравнений: ΣX = 0, ΣY=0. Очевидно, поставленная задача и соответствующая ей система будут статически неопределимыми.

2. Балка, жестко защемленная на левом конце и имеющая на правом конце шарнирно-неподвижную опору, загружена произвольной плоской системой сил (рис.27).

Такую задачу нельзя решить в рамках теоретической механики, предполагая рассматриваемое тело абсолютно твердым.

Рис.27

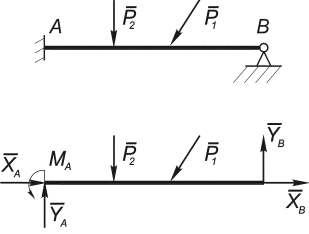
Вернемся к изучению составных систем, типичным представителем которых является трехшарнирная рама (рис. 28,а). Она состоит из двух тел: AC и BC, соединенным ключевым шарниром C. На примере этой рамы рассмотрим два способа определения опорных реакций составных систем.

1 способ. Рассмотрим тело AC, загруженное заданной силой Р, отбросив в соответствии с аксиомой 7 все связи и заменив их соответственно реакциями внешних (X_A, Y_A) и внутренних (X _C, Y_C) связей (рис. 28,б).

Напомним, что по условию задачи требовалось определить только 4 опорные реакции, нам же пришлось проделать дополнительную работу, определяя реакции в соединительном шарнире. В этом и заключается недостаток данного способа определения опорных реакций.

Полученная система состоит из двух тел и не является абсолютно твердым телом, поскольку расстояние между точками А и В может изменяться вследствие взаимного поворота обеих частей относительно шарнира С. Тем не менее можно считать, что совокупность сил, приложенных к раме АВС образует систему, если воспользоваться аксиомой отвердевания (рис.28,в).

Рис.28

Итак, для тела АВС можно составить три уравнения равновесия. Например:

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Источник

Нагрузка в теоретической механике

Вы будете перенаправлены на Автор24

При расчетах в теоретической механике встречается такое понятие как нагрузка. Она может распределяться вдоль заданной поверхности, согласно определенному закону.

Понятие нагрузки в теоретической механике

В качестве одного из важнейших понятий в теоретической механике выступает нагрузка. Она является мерой механического взаимодействия тел и становится определяющей для интенсивности и направления такого взаимодействия.

Механическим называется такое взаимодействие двух тел, которое способно изменять их кинематическое состояние.

Для классификации нагрузок в теоретической механике важное значение имеют такие понятия, как сила и момент (пара сил).

Силу определяют три элемента: числовое значение (модуль), точка приложения и направление. Изображением силы выступает вектор. Прямая, по которой такая сила направляется, выступает в качестве линии действия силы. Единицей силы в СИ считается ньютон (н).

Готовые работы на аналогичную тему

Классификация нагрузок в теоретической механике

Нагрузки в теоретической механике классифицируются в зависимости от их значения. Они бывают статистическими, повторно-переменными, динамическими, распределенными по поверхности или сосредоточенными.

Статистические нагрузки или остаются неизменными со временем или изменяются достаточно медленно. При действии таких нагрузок производится расчет прочности. Повторно-переменный вид нагрузок характеризуется многократным изменением только значения или еще дополнительно знака. Действие такого типа нагрузок провоцирует усталость металла.

Динамические нагрузки характеризуются изменением своего значения за короткий промежуток времени, способствуют большим ускорениям, вызывают силы инерции и провоцируют внезапное разрушение конструкции. В зависимости от способа приложения, нагрузки бывают: сосредоточенные или распределенные по поверхности.

Передача нагрузки между деталями на самом деле осуществляется не в одной точке, а на определенной площадке, нагрузка таким образом будет распределенной. В то же время, если размеры площадки контакта окажутся незначительными в сравнении с размерами самой детали, сила будет считаться сосредоточенной.

Замена распределенного типа нагрузки на сосредоточенную не требуется, если производятся расчеты реальных деформируемых тел. В сопротивлении материалов аксиомы теоретической механики применяются ограниченно. Не допускается:

Все вышеперечисленные действия способствуют изменению распределения внутренних сил в конструкции.

Распределенная и сосредоточенная нагрузка

В реальности зачастую встречаются силы, которые приложены не к самой точке, а к поверхности или объему тела. Речь может идти о силе тяжести, например, или давлении ветра. Нагрузка будет в таком случае восприниматься не бесконечно малой площадкой, а значительной площадью или объемом тела. Эти силы называются распределенными. Распределенная нагрузка с постоянной интенсивностью по всей длине участка считается равномерно распределенной

Примером такой нагрузки может быть снег, выпавший на крышу дома. Своей силой тяжести снежный покров оказывает давление на всю поверхность крыши, в равной степени нагружая при этом каждую единицу ее площади, а не отдельно взятую точку.

Источник

В чем измеряется распределенная нагрузка

Каждое здание или сооружение неизбежно испытывает воздействие тех или иных нагрузок. Это обстоятельство заставляет нас, расчетчиков, анализировать работу сооружения с позиции наиболее неблагоприятного их сочетания — чтобы даже в случае его проявления конструкция оставалась прочной, устойчивой, выносливой.

Для конструкции нагрузка является внешним фактором, который переводит ее из состояния покоя в напряженно-деформированное состояние. Сбор нагрузок не является конечной целью инженера — эти процедуры относятся к первому этапу алгоритма расчета конструкции (рассмотрен в этой статье).

Классификация нагрузок

В первую очередь, нагрузки классифицируют по времени воздействия на конструкцию:

Сегментация нагрузок позволяет моделировать работу конструкции и выполнять соответствующие расчеты более гибко, с учетом вероятности появления той или иной нагрузки и вероятности их одновременного появления.

Единицы измерения и взаимные преобразования нагрузок

В сфере строительства сосредоточенные силовые нагрузки измеряются, как правило, в килоньютонах (кН), а моментные нагрузки — в кНм. Напомню, что согласно Международной системе единиц (СИ) сила измеряется в Ньютонах (Н), длина — в метрах (м).

Распределенные по объему нагрузки измеряются в кН/м3, по площади — в кН/м2, по длине — в кН/м.

Рисунок 1. Виды нагрузок:
1 — сосредоточенные силы; 2 — сосредоточенный момент; 3 — нагрузка на единицу объема;
4 — нагрузка, распределенная по площади; 5 — нагрузка, распределенная по длине

Любую сосредоточенную нагрузку \(F\) можно получить, зная объем элемента \(V\) и объемный вес его материала \(g\):

Получить нагрузку, распределенную по площади элемента, можно через его объемный вес и толщину \(t\) (размер, перпендикулярный плоскости нагрузки):

\[p = g \cdot t.\quad (4.2)\]

Аналогично, распределенная по длине нагрузка получается произведением объемного веса элемента \(g\) на толщину и ширину элемента (размеры в направлениях, перпендикулярных плоскости нагрузки):

\[q = g \cdot t \cdot b = gA,\quad (4.3)\]

Кинематические воздействия измеряются в метрах (прогибы) или радианах (углы поворотов). Температурные нагрузки измеряются в градусах Цельсия (°C) или других единицах температуры, хотя могут задаваться и в единицах длины (м) или быть безразмерными (температурные расширения).

Постоянные нагрузки

К постоянным нагрузкам относятся:

Рассмотрим примеры определения нагрузки от собственного веса для различных элементов конструкций.

Кейс 1. Нагрузка от собственного веса балкона

Рисунок 2. Нагрузка от собственного веса балкона

Если принять расчетную схему балконной плиты в виде консольно-защемленной балки, то имеют место несколько видов нагрузок, которые можно считать постоянными:

Все эти нагрузки должны учитываться в расчете одновременно, потому что воздействуют на конструкцию постоянно, и все вместе. Таким образом, изгибающий момент в заделке будет равен:

где \(l\) — длина консольного свеса плиты.

Нагрузку от собственного веса отдельного элемента конструкции удобно вычислять через объемный вес материала, из которого он выполнен. Например, нагрузка от веса железобетонной плиты балкона (рис. 1):

Соответственно, для определения нагрузки от утеплителя в формуле (4.5) достаточно заменить объемный вес на вес 1 м 3 применяемого утеплителя, а вместо толщины плиты указать толщину слоя. Расчетная ширина полосы нагрузки \(b\) остается постоянной.

Нагрузку от веса перил можно вычислить так:

\[F = \left( <<\rho _c>\cdot A \cdot h> \right)n,\quad \left( <4.6>\right)\]

Кейс 2. Нагрузка от собственного веса металлоконструкций

Рассмотрим пример определения постоянной нагрузки, воздействующей на колонну металлического каркаса (рисунок 3).

Рисунок 3. Передача постоянной нагрузки от элементов каркаса

На колонны опираются несущие балки (двутавр N20) длиной \(l = 3\) м, на которые сверху уложен настил из листового проката толщиной \(t = 20\) мм. На каждую балку приходится доля нагрузки, собираемая с полупролета с каждой стороны, а в сумме — с целого пролета \(b = 4\) м между двумя соседними балками:

\[ = <\rho _s>\cdot b \cdot t = 78,5 \cdot 4 \cdot 0,020 = 6,28.\quad \left( <4.7>\right)\]

Определяем нагрузку от собственного веса балки (\(A\) — площадь сечения двутавра N20):

Балка, опертая по концам, “делится” 50% своей нагрузки с каждой из опор. Значит, на каждую колонну приходится половина общей нагрузки:

Кейс 3. Давление грунта на подпорную стенку

При проектировании подпорной стенки расчетчику сначала следует определить активное и пассивное давление грунта (рисунок 4):

Рисунок 4. Нагрузки от давления грунта

Сила \(\) является равнодействующей активного давления, воздействующего на стенку со стороны основного массива грунта. Соответственно, сила \(\) — равнодействующая пассивного давления (включается в работу, когда основной массив пытается сдвинуть стенку влево).

Указанные усилия определяются, как правило, по законам механики грунтов, с учетом высоты засыпки, свойств грунта и других параметров.

Кейс 4. Гидростатическая нагрузка на опору моста

На каждую мостовую опору, размещенную в русле реки или омываемую паводковыми водами на подходах, воздействует гидростатическое давление воды (рисунок 5).

Рисунок 5. Опора моста: 1 — по фасаду, 2 — поперек моста

То, что мы в обиходе называем “архимедовой силой”, является силой упругого взаимодействия физического объекта с жидкостью. Поскольку опора моста притоплена, то со стороны водотока на нее действует соответствующая выталкивающая сила:

\[F = \rho \cdot h \cdot b \cdot t,\quad \left( <4.10>\right)\]

Если в сооружении проявляются усилия, например, от предварительного напряжения (в ЖБК или металлоконструкциях с оттяжками или вантами), то эти усилия также относят к усилиям от постоянных нагрузок.

Почти все остальные виды нагрузок являются временными.

Длительные и кратковременные нагрузки

Длительные нагрузки оказывают воздействие на здание или сооружение в течение длительного срока (как говорится “не день и не два”):

Кратковременные нагрузки проявляются в коротких промежутках времени:

Как отличить длительную нагрузку от кратковременной?

Чтобы отличить длительную нагрузку от кратковременной, постарайтесь проанализировать срок ее “пребывания” на конструкции. Если, появившись, она тут же может исчезнуть — смело относите ее к кратковременным, иначе — к длительным.

Кейс 5. Временная нагрузка от веса людей и перегородок

Рассмотрим ситуацию, когда нам нужно спроектировать плиту перекрытия торгового центра. На рисунке 6 показана проектная схема здания с секциями различного назначения, в которых могут пребывать люди. Красным цветом показаны места теоретического расположения перегородок (идея архитектора).

Рисунок 6. Фасад и сечение конструкции (сверху) и расчетная схема перекрытия (снизу)

В данном случае мы имеем дело с двумя временными нагрузками — весом перегородок (длительная нагрузка) и весом людей (кратковременная нагрузка). Обычно, ширина перегородки существенно меньше пролета здания в свету, поэтому в плоской расчетной схеме данная нагрузка может быть принята в виде сосредоточенной силы:

\[F = \gamma \cdot b \cdot h \cdot t,\quad (4.11)\]

Посетители и персонал торгового центра могут произвольным образом располагаться между стенами и перегородками, поэтому вес людей принимаем в виде равномерно распределенной нагрузки нормативной интенсивностью не ниже 4 кПа [7]:

\[q = 4,0 \cdot b.\quad (4.12)\]

Кстати, располагать все временные нагрузки сразу во всех пролетах конструкции — не совсем правильно, но об этом мы поговорим позже.

Кейс 6. Снеговая и ветровая нагрузки на рекламный щит

Рассмотрим сбор снеговых и ветровых нагрузок на конструкции наружной рекламы типа “биллборд” (рисунок 7, 1).

Рисунок 7. К расчету биллборда на снеговые нагрузки:
1 — общий вид; 2, 3 — сбор снеговых нагрузок по фасаду; 4 — вид сбоку

Начнем со снеговой нагрузки. Обычное выпадение снега на верхнюю кромку щита учитываем в расчете равномерно распределенной нагрузкой интенсивностью \(q\) (рисунок 7, 2).

Конструкция щита имеет элементы освещения, поэтому можно предположить, что снег в этом месте может накапливаться, цепляясь за стойку. Моделируя эту ситуацию, приходим к неравномерно распределенной нагрузке (рисунок 7, 3).

Величина снеговой нагрузки зависит от норм, по которым Вы выполняете расчет. Так, в нормах [7] формула для определения снеговой нагрузки (кПа) имеет вид:

Все величины, входящие в формулу (4.13), приводятся непосредственно в стандарте [7]. Тогда нагрузка на кромку щита (кН/м) будет равна:

Сосредоточенная сила, которая может далее потребоваться для проверки прочности стойки щита на сжатие, в первом случае составляет

а для случая c неравномерным распределением снеговая нагрузка собирается с соответствующих участков длиной \(a\), \(b\):

Еще одной проблемой для рекламного щита может стать наледь, которая появляется на открытых невертикальных поверхностях в холодное время года. Осадки в виде снега или дождя могут образовать сплошную полосу льда, которая создаст дополнительную нагрузку на конструкции щита. В этом случае модель нагрузки будет аналогична представленной на рисунке 7, 1.

Безусловно, для таких сравнительно небольших конструкций, как биллборд, снеговая нагрузка не будет доминирующей, и в большинстве случаев ее можно не учитывать. Однако, при проектировании конструкций с большей площадью горизонтальной поверхности снеговая нагрузка будет возрастать и может привести к появлению существенных усилий в опорных элементах. Вот пример конструкции, в проекте которой снеговая нагрузка была учтена ошибочно:

Рисунок 8. Чрезмерные прогибы крыши от снеговой нагрузки

Современные нормы проектирования предписывают учитывать воздействие ветра в различных его проявлениях (вихревое возбуждение, галопирование, флаттер и пр.). В данном примере определим только основной тип ветровой нагрузки из стандарта [7].

Рисунок 9. К расчету биллборда на ветровые нагрузки:
1 — вид по фасаду; 2 — вид сбоку

Главным образом, на конструкцию действует нормальное давление ветра \(\). Современные стандарты проектирования, например [7], определяют ветровую нагрузку (кПа) как сумму двух составляющих:

Средняя и пульсационная составляющие, в свою очередь, зависят от ветрового района, скорости ветра, размеров сооружения (в первую очередь, высоты) и других параметров.

Основное полотно биллборда (щит) выступает своеобразным “парусом”, собирающим ветровую нагрузку, поэтому основное внимание в расчетах следует сосредоточить на проверках прочности соединения щита со стойкой, и самой стойки. При расчете стойки необходимо рассмотреть все возможные варианты ее работы — от изгиба в обеих плоскостях (\(xz\), \(yz\)) до кручения вокруг продольной оси (\(z\)).

Сила трения ветрового потока о конструкции щита будет возникать на конструкциях с “волнистой” или шероховатой структурой. Для биллбордов с относительно гладкой поверхностью она будет незначительна.

Особые нагрузки

Особые нагрузки отнесены в отдельную категорию, потому что их появление связано с каким-либо аварийным происшествием, природной или техногенной катастрофой:

Ярким примером особой нагрузки является террористическая атака на башни Всемирного торгового центра 11 сентября 2001 года в Нью-Йорке, США:

Рисунок 10. Задача: какой жесткостью должно обладать здание, чтобы не разрушиться от удара самолета?

Для определения особой нагрузки расчетчику, как правило, придется воспользоваться соответствующим специализированным стандартом (например, для проектирования сейсмостойких или пожароустойчивых конструкций).

Нормативные (характеристические) и расчетные нагрузки

До этого момента мы говорили о нагрузки, подразумевая ее какое-то числовое значение. В проектировании строительных конструкций различают два вида значений нагрузки:

Нормативное значение нагрузки — это значение, полученное по фактическим размерам и весовым характеристикам элемента. Например, если нормативная нагрузка от веса 1 м 3 железобетона составляет примерно 25 кН; это означает, что если мы положим такой кубик на весы, то стрелка покажет нам значение 2,5 т.

Термин “нормативная” нагрузка больше относится к нормам проектирования СНГ, в Еврокоде же используется понятие “характеристическое” значение нагрузки [3].

Непосредственно в расчетах используется расчетное значение нагрузки. По сути, это нормативное значение, только с учетом различных коэффициентов. Например, расчетное значение нагрузки от собственного веса железобетонной балки составляет [7]:

Таким образом, расчетная нагрузка повышается на 10% по сравнению с нормативной.

Коэффициент надежности

В нормах проектирования СНГ коэффициент надежности по нагрузке обозначается \(<\gamma _f>\).

Как правило, он всегда больше единицы, потому что в расчет нам нужно завести заведомо большую нагрузку. Величина коэффициента надежности для постоянных нагрузок колеблется в диапазоне от 1,05 до 1,3.

Для временных нагрузок коэффициенты надежности обычно выше, чем для постоянных. Это обусловлено тем, что временная нагрузка по природе более изменчива и вероятность отклонения ее значения от нормативного, в общем случае, выше. Так, расчетная нагрузка от веса людей составляет:

Источник