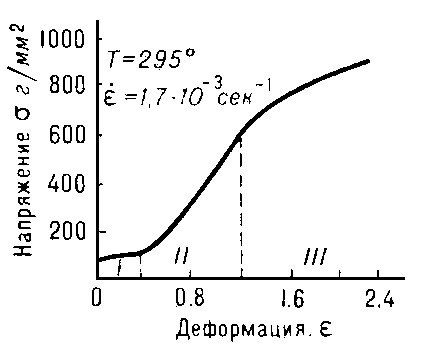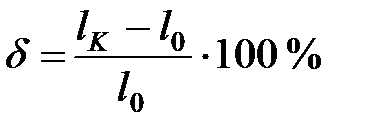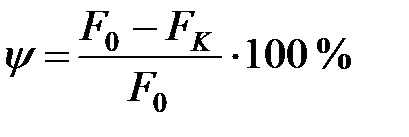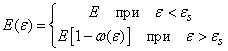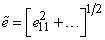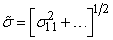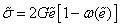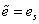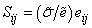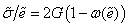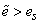в чем измеряется пластичность
Пластичность (физика)
 Механика сплошных сред Механика сплошных сред | ||||||||||
 | ||||||||||
| Сплошная среда | ||||||||||
| ||||||||||
| См. также: Портал:Физика |
Пласти́чность — способность материала без разрушения получать большие остаточные деформации. Свойство пластичности имеет решающее значение для таких технологических операций, как штамповка, вытяжка, волочение, изгиб и др. Мерой пластичности являются относительное удлинение δ и относительное сужение ψ, определяемые при проведении испытаний на растяжение. Чем больше δ, тем более пластичным считается материал. По уровню относительного сужения ψ можно делать вывод о технологичности материала. К числу весьма пластичных материалов относятся отожженная медь, алюминий, латунь, золото, малоуглеродистая сталь и др. Менее пластичными являются дюраль и бронза. К числу слабо пластичных материалов относятся многие легированные стали.
У пластичных материалов прочностные характеристики на растяжение и сжатие сопоставляют по пределу текучести. Принято считать, что σт.р≈σт.с.
Деление материалов на пластичные и хрупкие является условным не только потому, что между теми и другими не существует резкого перехода в значениях δ и ψ. В зависимости от условий испытания многие хрупкие материалы способны вести себя как пластичные, а пластичные — как хрупкие.
Очень большое влияние на проявление свойств пластичности и хрупкости оказывают скорость натяжения и температура. При быстром натяжении более резко проявляется свойство хрупкости, а при медленном — свойство пластичности. Например, хрупкое стекло способно при длительном воздействии нагрузки при нормальной температуре получать остаточные деформации. Пластичные же материалы, такие как малоуглеродистая сталь, под воздействием резкой ударной нагрузки проявляют хрупкие свойства.
Литература
Феодосьев В.И. Сопротивление материалов. — М.: Изд-во МГТУ им. Н.Э. Баумана, 1999. С. 86. ISBN 5-7038-1340-9
См. также
Полезное
Смотреть что такое «Пластичность (физика)» в других словарях:
Пластичность (свойство твёрдых тел) — Пластичность (от греч. plastikós ‒ годный для лепки, податливый, пластичный), свойство твёрдых тел необратимо изменять свои размеры и форму (т. е. пластически деформироваться) под действием механических нагрузок. П. кристаллических тел (или… … Большая советская энциклопедия
ФИЗИКА. — ФИЗИКА. 1. Предмет и структура физики Ф. наука, изучающая простейшие и вместе с тем наиб. общие свойства и законы движения окружающих нас объектов материального мира. Вследствие этой общности не существует явлений природы, не имеющих физ. свойств … Физическая энциклопедия
Пластичность — I Пластичность (от греч. plastikós годный для лепки, податливый, пластичный) свойство твёрдых тел необратимо изменять свои размеры и форму (т. е. пластически деформироваться) под действием механических нагрузок. П. кристаллических тел… … Большая советская энциклопедия
Физика твёрдого тела — Физика твёрдого тела раздел физики конденсированного состояния, задачей которого является описание физических свойств твёрдых тел с точки зрения их атомарного строения. Интенсивно развивалась в XX веке после открытия квантовой механики.… … Википедия
Атомная физика — раздел физики, в котором изучают строение и состояние атомов. А. ф. возникла в конце 19 начале 20 вв. В 10 х гг. 20 в. было установлено, что атом состоит из ядра и электронов, связанных электрическими силами. На первом этапе своего… … Большая советская энциклопедия
Твёрдое тело — одно из четырёх агрегатных состояний вещества, отличающееся от др. агрегатных состояний (жидкости (См. Жидкость), Газов, плазмы (См. Плазма)) стабильностью формы и характером теплового движения атомов, совершающих малые колебания около… … Большая советская энциклопедия
ТВЁРДОЕ ТЕЛО — агрегатное состояние в ва, характеризующееся стабильностью формы и хар ром теплового движения атомов, к рые совершают малые колебания вокруг положений равновесия. Различают крист. и аморфные Т. т. Кристаллы характеризуются пространств.… … Физическая энциклопедия
Механика — (греч. μηχανική искусство построения машин) область физики, изучающая движение материальных тел и взаимодействие между ними. Движением в механике называют изменение во времени взаимного положения тел или их частей в пространстве[1].… … Википедия
Гидродинамика — Механика сплошных сред … Википедия
Теория упругости — Механика сплошных сред … Википедия
Пластичность
Полезное
Смотреть что такое «Пластичность» в других словарях:
ПЛАСТИЧНОСТЬ — Изящность форм; образность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЛАСТИЧНОСТЬ Изящность форм; образовательность. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их … Словарь иностранных слов русского языка
Пластичность — – свойство огнеупорной формовочной массы изменять форму под действием внешней механической нагрузки без нарушения сплошности и сохранять ее после прекращения действия нагрузки. [ГОСТ Р 52918 2008] Пластичность – свойство твердых тел… … Энциклопедия терминов, определений и пояснений строительных материалов
ПЛАСТИЧНОСТЬ — ПЛАСТИЧНОСТЬ, пластичности, мн. нет, жен. отвлеч. сущ. к пластичный. Пластичность движений. Пластичность художественного изображения. Пластичность раскаленного добела железа. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
пластичность — легкость, плавность, изящество, пластика, изящность, термопластичность, податливость, гармоничность, грация, грациозность, мягкость, гибкость, тонкость, соразмерность Словарь русских синонимов. пластичность 1. см. изящество. 2. см … Словарь синонимов
ПЛАСТИЧНОСТЬ — (от греческого plastikos годный для лепки, податливый), свойство твердого тела сохранять так называемую остаточную деформацию частично (упругопластическое состояние) или полностью (пластическое состояние) после снятия внешнего механического… … Современная энциклопедия
ПЛАСТИЧНОСТЬ — (от греч. plastikos годный для лепки, податливый), свойство материалов тв. тел сохранять часть деформации при снятии нагрузок, к рые её вызвали. Пластич. деформации испытывают детали конструкций и сооружений, заготовки при обработке давлением… … Физическая энциклопедия
Пластичность — (от греческого plastikos годный для лепки, податливый), свойство твердого тела сохранять так называемую остаточную деформацию частично (упругопластическое состояние) или полностью (пластическое состояние) после снятия внешнего механического… … Иллюстрированный энциклопедический словарь
ПЛАСТИЧНОСТЬ — (от греч. plastikos годный для лепки податливый), свойство твердых тел необратимо деформироваться под действием механических нагрузок. Пластичность определяет возможность обработки материалов давлением (ковки, прокатки и др.) … Большой Энциклопедический словарь
Пластичность — (от греч. plastikуs годный для лепки, податливый, пластичный), качество, присущее скульптуре, художественная выразительность объёмной формы, гармоничное соотношение выразительности моделировки с весомостью, внутренней наполненностью,… … Художественная энциклопедия
пластичность — пластичность. См. генетическая пластичность. (Источник: «Англо русский толковый словарь генетических терминов». Арефьев В.А., Лисовенко Л.А., Москва: Изд во ВНИРО, 1995 г.) … Молекулярная биология и генетика. Толковый словарь.
ПЛАСТИЧНОСТЬ — ПЛАСТИЧНОСТЬ, способность металлов и некоторых других материалов растягиваться без уменьшения прочности. Говорят, что медь обладает тягучестью, поскольку она легко вытягивается в проволоку, а золото и серебро являются еще более тягучими.… … Научно-технический энциклопедический словарь
Показатели прочности и пластичности материала



Показатели прочности:
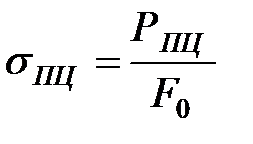
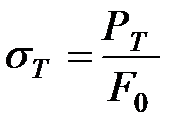
Если на кривой деформации отсутствует четко выраженная площадка текучести (рис. 7, а), то определяют предел текучести условный.
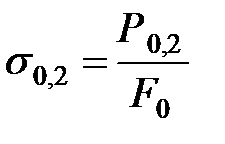
5. Сопротивление значительным пластическим деформациям (для пластичных материалов) характеризуется пределом прочности.
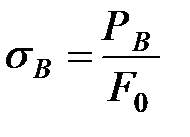
Показатели пластичности:
Для определения длины расчетной части lK после разрыва части образца плотно прикладывают друг к другу (рис. 8) и измеряют расстояние между метками, которые ограничивали начальную расчета длину.
Способы определения твердости материалов.
Твердость — способность материала сопротивляться упругой и пластической деформации при внедрении в него более твердого тела (индентора).
Определение твердости по методу Роквелла
Схема измерения твердости по Роквеллу
Сначала индентор вдавливается в поверхность образца под предварительной нагрузкой Р0 = 100 Н, которая не снимается до конца испытания, что позволяет повысить точность испытаний, т.к. исключает влияние вибраций и тонкого поверхностного слоя. Под нагрузкой Р0 индентор погружается в образец на глубину h0. Затем на образец подается полная нагрузка Р = Р0 + Р1, глубина вдавливания увеличивается. Последняя после снятия основной нагрузки Р1 (на индентор вновь действует только предварительная нагрузка Р0) определяет число твердости по Роквеллу (HR). Чем больше глубина вдавливания h, тем меньше число твердости HR.
| Примерная твердость по Бринеллю | Шкала Роквелла | Тип индентора | Общая нагрузка | Допускаемые величины твердости по шкале |
| Н | кгс | |||
| Менее 228 | Шкала В (красная) | стальной шарик | 25-100 | |
| 229-682 | Шкала С (черная) | алмазный конус | 22-68 | |
| 363-720 | Шкала А (черная) | алмазный конус | 70-85 |
Существенное значение имеет толщина испытуемого образца. После замера твердости на обратной стороне образца не должно быть следов отпечатка.
Во всех случаях измерений значение предварительной нагрузки постоянно и равно Р0 = 100 Н.
Число твердости выражается формулами:
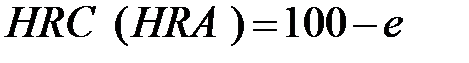
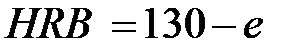
Таким образом, единица твердости по Роквеллу безразмерная величина, соответствующая осевому перемещению индентора на 0,002 мм.
Существует несколько типов приборов для измерения твердости по Роквеллу, но принципиальные схемы их работы аналогичны.
Определение твердости по методу Виккерса
При стандартном измерении твердости по Виккерсу (ГОСТ 2999-75) в поверхность образца вдавливается алмазный индентор в форме четырехгранной пирамиды с углом при вершине a»136°. После удаления нагрузки P (10¸1000 Н), действовавшей определенное время (10-15 с), измеряют диагональ отпечатка d, оставшегося на поверхности образца.
Число твердости HV определяют по формуле:
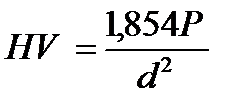
Число твердости записывается без единиц измерения, например 230 HV. Если число твердости выражают в МПа, то после него указывают единицу измерения, например HV = 3200 МПа.
Относительно небольшие нагрузки и малая глубина вдавливания индентора обуславливают необходимость более тщательной подготовки поверхности, чем при измерении твердости по Бринеллю. Образцы, как правило, полируют, с поверхности снимается наклеп.
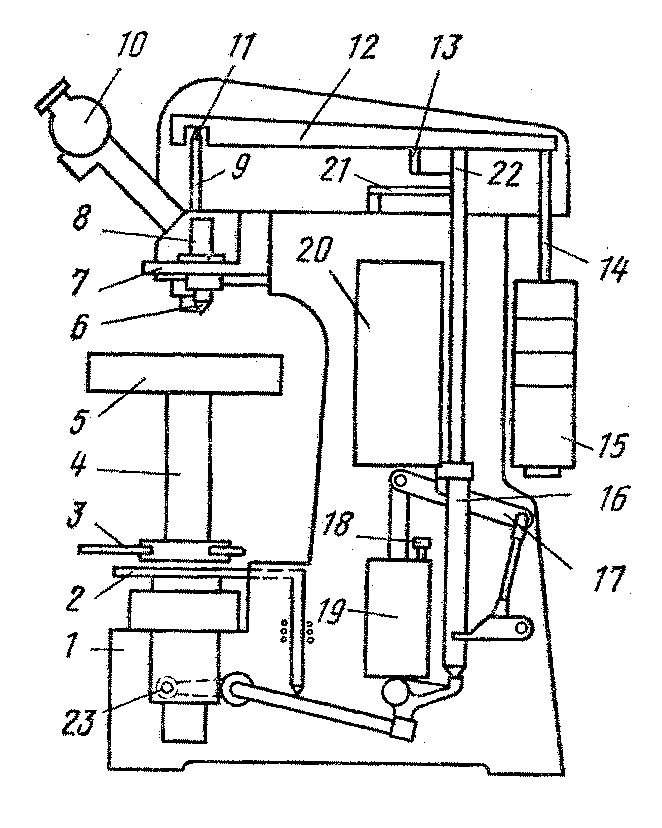
Измерения осуществляют на приборах марки ТП. Прибор смонтирован на станине 1. Образец помещают на опорный столик 5. Нагрузка прилагается к индентору 6 через установленный на призмах рычаг. Рычаг с подвеской 14 без сменных грузов 15 обеспечивает минимальную нагрузку 50 Н.
Схема прибора ТП для определения твердости по Виккерсу:
После установки образца на столик 5 совмещают перекрестие окуляра микроскопа 10 с тем местом на образце, твердость которого необходимо измерить. Наводят на резкость, устанавливают индентор над образцом, включают механизм грузового привода. Пока образец находится под нагрузкой, горит сигнальная лампочка, расположенная в верхней части передней панели твердомера.
После снятия нагрузки поворотную головку переводят в такое положение, чтобы полученный отпечаток вновь был виден в микроскоп. Затем с помощью барабанчика окуляр-микрометра замеряют длину диагонали отпечатка.
Хрупкое и вязкое разрушение материала.
При хрупком разрушении макропластическая деформация отсутствует. В металле возникает только упругая деформация. Разрушение происходит путем отрыва или скола, когда плоскость разрушения перпендикулярна действующим напряжениям. Разрушение начинается от дефекта (микротрещины), вблизи которого концентрируются напряжения, превосходящие теоретическую прочность металла.
При вязком разрушении металл претерпевает значительную пластическую деформацию. У пластичных материалов, благодаря релаксации напряжений, их концентрация вблизи несплошностей оказывается недостаточной и развитие трещин скола (т.е. хрупких) не происходит. Вязкое разрушение происходит путем сдвига.
Пластичность (физика)
У пластичных материалов прочностные характеристики на растяжение и сжатие сопоставляют по пределу текучести. Принято считать, что σт.р≈σт.с.
Деление материалов на пластичные и хрупкие является условным не только потому, что между теми и другими не существует резкого перехода в значениях δ и ψ. В зависимости от условий испытания многие хрупкие материалы способны вести себя как пластичные, а пластичные — как хрупкие.
Очень большое влияние на проявление свойств пластичности и хрупкости оказывают скорость натяжения и температура. При быстром натяжении более резко проявляется свойство хрупкости, а при медленном — свойство пластичности. Например, хрупкое стекло способно при длительном воздействии нагрузки при нормальной температуре получать остаточные деформации. Пластичные же материалы, такие как малоуглеродистая сталь, под воздействием резкой ударной нагрузки проявляют хрупкие свойства.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Термической (или тепловой) обработкой называется совокупность операций нагрева, выдержки и охлаждения твёрдых металлических сплавов с целью получения заданных свойств за счёт изменения внутреннего строения и структуры. Тепловая обработка используется либо в качестве промежуточной операции для улучшения обрабатываемости давлением, резанием, либо как окончательная операция технологического процесса, обеспечивающая заданный уровень свойств изделия.
Диагра́мма фа́зового равнове́сия (диаграмма состоя́ния) желе́зо—углеро́д (иногда эту диаграмму называют «диаграмма железо—цементит») — графическое отображение фазового состояния сплавов железа с углеродом в зависимости от их химического состава и температуры.
Твёрдые растворы — фазы переменного состава, в которых атомы различных элементов расположены в общей кристаллической решётке.
ПЛАСТИЧНОСТЬ
ПЛАСТИЧНОСТЬ – свойство твердых тел изменять форму и размеры под влиянием внешних нагрузок и сохранять ее, когда нагрузки перестают действовать (после снятия нагрузок).
Первое представление о свойстве материала, называемом пластичностью, дает комок пластилина, который под давлением пальцев легко меняет форму, и сохраняет новую форму после действия на него (в отличие о растянутой пружинки, которая опять сожмется, если ее отпустить В этом смысле говорят, что пружинка упруга, а пластилин пластичен. Пластилин и пластичность – слова одного корня, от греческого слова пластика, что значит лепка, от глагола «лепить» (из глины).
Чтобы получить более точное представление о свойстве пластичности, можно сделать (или представить себе) простой опыт. Пусть есть вытянутый параллелепипед (стержень) из пластилина, длинное ребро которого составляет приблизительно 10 см, а малая грань представляет собой квадрат 1 см × 1 см. Пусть этот стержень опирается концами на две опоры («мостик»). Если на средину стержня класть металлические грузики (например, монеты), то пока нагрузка невелика, изменение формы стержня на глаз незаметно. При дальнейшем нагружении обнаруживается, что в некоторый момент стержень прогибается и становится криволинейным. Если убрать все грузики, криволинейная форма все равно сохранится.
Этот опыт показывает, что стержень из материала, обладающего свойством пластичности, сопротивляется действию нагрузок, почти не изменяя свою форму, до тех пор, пока нагрузка не превысит некоторый порог, после чего происходит заметное изменение формы, сохраняющееся и после снятия нагрузки. В этом суть пластичности, но не вся – изменение формы (деформирование) зависит только от приложенной нагрузки и не изменяется само по себе с течением времени. Если деформирование при неизменной нагрузке все же происходит, то материал называют не пластическим, а вязкопластическим или вязкоупругим (см. РЕОЛОГИЯ; ПОЛЗУЧЕСТЬ). Конечно, пластилин – это знакомый и наглядный пример пластического материала. Важно то, что свойство пластичности присуще очень многим конструкционным материалам. В первую очередь, это – металлы и сплавы – сталь, железо, медь, алюминий и другие, но представление о пластическом деформировании оказывается очень полезным и для понимания процессов деформирования композиционных материалов, в том числе металлокерамических, углеродных и полимерных.
Пластичность материала как бы противопоставлена упругости: пластическое тело сохраняет приданную ему форму, а упругое – восстанавливает первоначальную. Но пластичность противопоставляется еще и хрупкости: пластическое тело отвечает на увеличение нагрузки заметным изменением формы, а хрупкое (например, стекло) – появлением трещин и разрушением.
Изучение пластичности развивается по двум направлениям: одно из них связано, в первую очередь, с проблемами техники и цель его – ответ на вопрос: если конструкция подвергается воздействию внешних сил известной величины, каково при этом меняется форма – т.е. как она деформируется? Это важно знать конструктору, но есть и еще одно важное обстоятельство: обычно пластичность предшествует разрушению, так что изучение пластических деформаций является основой прогноза прочности и долговечности конструкции.
Второе направление изучения пластичности – это исследование того, что происходит в материале, как говорят, на микроуровне, т.е., что происходит внутри материала, например, при пластическом изгибе балки. Можно, по аналогии с опытом на изгиб стержня, сделать опыт на его растяжение: верхний конец стержня (его обычно называют образцом) закрепляют, а к нижнему прикладывают нагрузку. В этом случае заметить на глаз изменение длины образца трудно, но если измерять деформации специальными приборами, то обнаруживается, что процесс деформирования оказывается похожим на тот, что и в опыте с изгибом: при постепенном возрастании растягивающей нагрузки сначала проявляются очень малые упругие деформации, когда же нагрузка достигает порогового значения, то деформации (теперь уже, в основном, пластические) становятся, во-первых, более существенными, а, во-вторых, необратимыми (т.е. не исчезают после снятия нагрузки).
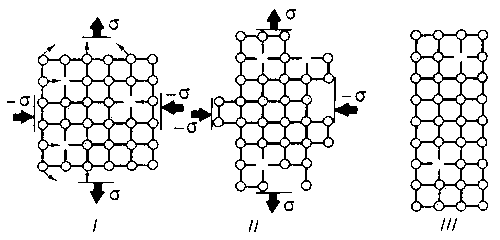
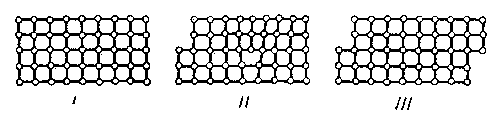
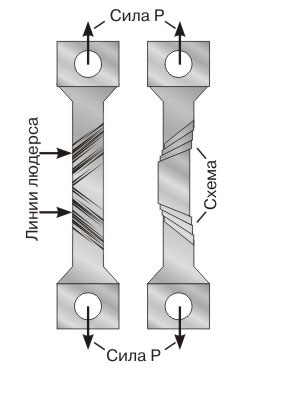
При этом обнаруживаются интересные явления. Если в опыте на растяжение использовать стальной образец в виде длинной пластинки с полированной (зеркальной) поверхностью, то в процессе пластического деформирования на этой поверхности появляется много близких тонких параллельных прямых линий, ориентированных под углом 45° к оси образца (ось образца – здесь прямая линия, проходящая посредине пластинки, параллельно ее длинным сторонам). Эти линии называются линиями Людерса – Чернова (по фамилиям открывших их ученых).
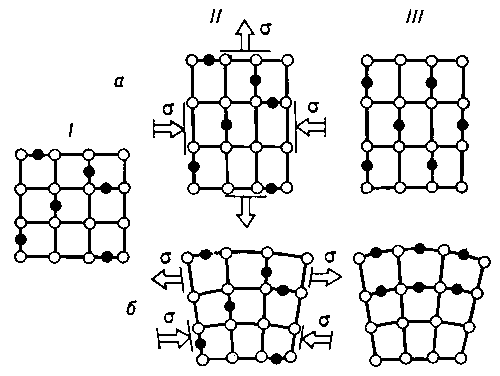
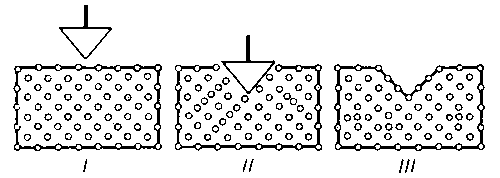
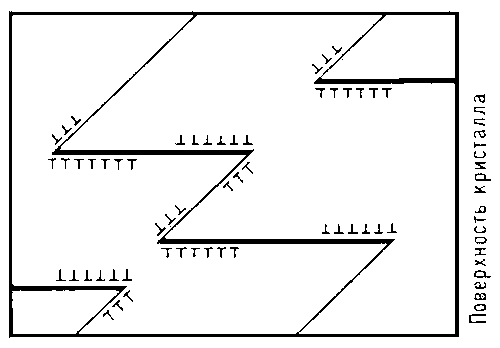
Микроскопический анализ этих линий показывает, что они появляются в результате того, что в материале пластинки происходит сдвиг, т.е. один тонкий слой как бы сдвигается относительно второго, второй – относительно третьего и т.д., как карты в колоде. Можно сказать, что линии Людерса – Чернова и есть границы сдвигающихся слоев. На рис.1 схематически изображена картина такого деформирования. Эта схема позволяет понять, как такие сдвиги приводят к пластическому удлинению образца и почему после снятия нагрузки пластические деформации не исчезают. Более сложные и точные опыты показали, что пластические деформации металлов и сплавов всегда вызываются сдвигами внутри материала. Кроме того, в пористых материалах происходят деформации, по внешним проявлениям очень сходные с пластическими, но связанные с уменьшением пор. Наиболее знакомым пористым материалом является пенопласт; в технике пористые материалы создает порошковая металлургия, где детали прессуются из металлического порошка.
Можно довольно точно описать картину деформирования, считая, что упругие деформации тела – это результат изменения расстояния между атомами, из которых оно состоит, а пластические деформации – результат сдвигов.
Итак, пластичность – результат сдвигов. А как происходят сами сдвиги? На этот вопрос (и на многие другие) отвечают разделы физики: физика твердого тела, теория дислокаций, физика металлов и т.д.
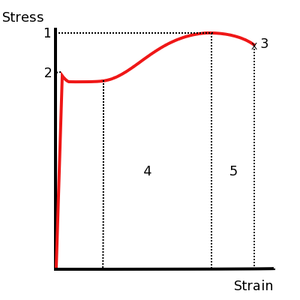
Таковы два направления, по которым исследуется пластичности, первое называется феноменологическим – оно изучает феномен пластичности так, как его можно наблюдать в опытах с образцами и нагрузками, и не опирается на результаты микроскопических опытов. Феноменологическое изучение пластичности металлов начинается с классического опыта на растяжение. Его результаты представляются в виде графиков (рис. 2), где по вертикальной оси откладывается напряжение s, равное растягивающей силе P, отнесенной к площади сечения образца F, т.е.
а по горизонтали – деформация образца e, равная удлинению dl образца (под действием силы P), отнесенному к его первоначальной длине l.
На рис. 2 изображен график, который называется «кривой растяжения»; материал – одна из марок стали. В начале нагружения (на графике от точки O до точки A) напряжение и деформация оказываются пропорциональными, т.е. имеет место закон Гука. Коэффициент пропорциональности называется модулем упругости (или модулем Юнга) E. Точка A на графике называется пределом упругости – после нее пропорциональность, свойственная упругости, сменяется криволинейной зависимостью, причем теперь деформация растет значительно быстрее, чем напряжение. Если в некоторой точке B мы начнем уменьшать напряжение (это называется разгрузкой), то на графике получится кривая, мало отличающаяся от прямой – BC со стрелкой вниз. Если, доведя напряжение до нуля, снова его увеличивать, на графике получится кривая CB1 (со стрелкой вверх), причем далее эта кривая плавно перейдет в кривую B1D, которая получилась бы при деформировании образца без разгрузки. Для простоты обычно обе кривые, BC и CB1, заменяют отрезком прямой B2C, который параллелен отрезку OA.
Есть несколько вариантов теории пластичности, которые отличаются, с одной стороны, тем, насколько точно они учитывают реальные особенности процесса деформирования упруго-пластического материала, и, с другой стороны, используемым математическим аппаратом. Одни теории являются менее точными, но более простыми и удобными для расчетов, что очень важно, так как расчет пластических деформаций в телах сложной формы представляет собой очень трудную задачу даже при использовании современных компьютеров. Другие теории могли бы обеспечить высокую точность, но приводят к очень большим трудностям, как математическим, так и экспериментальным. По-видимому, создание «идеальной» теории, сочетающей физическую наглядность, математическую простоту и в то же время обеспечивающей адекватное описание процессов пластического деформирования, является делом будущего. Но даже «простые» теории пластичности на самом деле достаточно сложны, так как требуют знания и понимания многих экспериментальных результатов и серьезной математической подготовки. В качестве примера можно рассмотреть идею самой простой теории пластичности.
В самом простом случае опыта на растяжение образца процесс упругого деформирования описывается законом Гука
За пределом упругости пропорциональности нет, но экспериментальную кривую растяжения можно описать, если считать, что модуль упругости E при этом перестает быть постоянной величиной и становится функцией деформации, т.е.
В этих формулах появляется новая функция w = w(e), которая называется функцией пластичности и должна быть найдена из экспериментальных данных.
Видно, что функция w(e) тождественно равна нулю при упругих деформациях и возрастает при пластических. Тогда ясно, что и упругие, и пластические деформации описываются уравнением, обобщающим закон Гука
Это уравнение описывает кривую деформирования, из которой оно, по существу, и получено и это так, пока речь идет только об опыте на растяжение. Но теория пластичности должна «уметь» описывать любые процессы деформирования – например, и кручение, и изгиб, и их совместное проявление, а для этого формулу необходимо существенно обобщить и сформулировать аналогичные по сути, но неизмеримо более сложные соотношения, которые связывали бы шесть компонент тензора деформаций с шестью компонентами тензора напряжений. Здесь и начинаются сложности.
Классическая деформационная теория называется «теорией малых упругопластических деформаций». Эта теория основана на трех экспериментальных фактах:
1. При различных упругопластических деформациях в каждой точке тела существует универсальная функциональная зависимость между среднеквадратичным значением сдвиговых деформаций и аналогичным среднеквадратичным значением сдвиговых напряжений.
2. При упругопластическом деформировании материала изменение объема всегда происходит упруго.
3. Первые два утверждения справедливы только при условии, что все внешние силы, действующие на тело, возрастают пропорционально друг другу (точнее – пропорционально одному параметру, например, времени). Это так называемое «простое» или «пропорциональное» нагружение.
Чтобы правильно понять эти три утверждения, нужно принять во внимание следующее:
Теория пластичности, как и все эмпирические теории, по своему существу является теорией приближенной. Это означает, что при известных условиях, когда она может описывать физическую реальность («условия применимости»), эмпирическая теория эту реальность описывает с относительно небольшой, но всегда присутствующей погрешностью (проще говоря, с небольшой ошибкой).
Теория пластичности, о которой идет речь, может дать ответ с погрешностью, близкой к 10%. И почти всегда такая погрешность оказывается вполне приемлемой – говорят, что «теория хорошо работает».
Математическая формулировка теории: пусть есть тензор деформации e ij и тензор напряжений sij. Требуется написать формулы (соотношения), которые связывают эти тензоры при малых упругопластических деформациях, подобно тому, как закон Гука связывает их при упругих деформациях.
Учитывая различные закономерности объемного и сдвигового деформирования, можно разделить тензоры на объемную (шаровую) и сдвиговую (девиаторную) части:
Следующий шаг – установление связи сдвиговых напряжений с деформацииями, поскольку пластичность – это сдвиги.
Для девиатора деформаций среднеквадратичный сдвиг в данной точке определяется формулой
Аналогично, среднеквадратичное сдвиговое напряжение определяется:
(величины 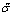
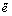
Это и есть универсальная функциональная зависимость между 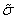
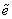
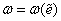
В пределах упругости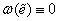
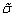
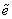
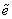
Это условие называется условием пластичности Хубера – Мизеса. Таким образом, можно окончательно записать
Второй постулат записывается в виде: s = KQ
где s – среднее нормальное напряжение (давление) в данной точке, а Q – относительное изменение объема малой частицы, окружающей эту точку. Число K > 0 называется объемным модулем упругости. Таким образом, относительное изменение объема малой частицы пропорционально среднему нормальному напряжению в этой частице.
Теперь можно записать определяющие соотношения теории малых упругопластических деформаций:
Девиаторы напряжений и деформаций связаны пропорциональной зависимостью
Коэффициент пропорциональности за пределами упругости перестает быть постоянным и становится переменной величиной:
Функция 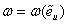
Шаровые тензоры напряжений деформаций всегда пропорциональны
или, что эквивалентно,
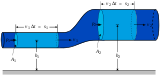
Все это справедливо только при пропорциональном нагружении, которое иногда называют простым, так как сложное нагружение – это непропорциональное нагружение. Оказывается, что в опыте, когда трубка подвергается растяжению силой P и кручению моментом M, деформации будут различными, в зависимости от того, как прикладываются нагрузки: сразу обе, сначала M, потом P, или наоборот. Это обстоятельство приводит к тому, что теорию пластичности при сложном нагружении уже нельзя построить по аналогии с теорией упругости.
Приведенная теория была разработана, экспериментально и теоретически обоснована и внедрена в инженерную практику работами А.Ильюшина, который опирался на работы своих предшественников – в первую очередь, Х.Хенки и Р.фон Мизеса.
Ильюшин А.А., Ленский В.С. Сопротивление материалов, М., Физматгиз, 1959;
Гордон Дж. Почему мы не проваливаемся сквозь пол? М., Изд-во «Мир», 1971;
Безухов Н.И. Основы теории упругости, пластичности и ползучести. М., Изд-во «Высшая школа», 1981