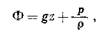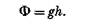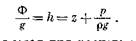в чем измеряется градиент давления

ГРАДИЕНТ ДАВЛЕНИЯ

Горизонтальная составляющая Г. д.— горизонтальный барический градиент — направлен по нормали к изобаре в горизонтальной плоскости в сторону убывания давления. Практически определяется падением давления на расстоянии, равном 100 км и определяемом по нормали к изобаре. Г. д. достигает наибольших значений в смерчах и тропических циклонах. По величине Г. д. определяют скорость ветра. См. Геострофический ветер.

Смотреть что такое «ГРАДИЕНТ ДАВЛЕНИЯ» в других словарях:

ГРАДИЕНТ ДАВЛЕНИЯ — см. Градиент барический. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь

ГРАДИЕНТ ДАВЛЕНИЯ — понижение давления, отнесенное к единице длины пути. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

градиент давления — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN pressure gradient … Справочник технического переводчика

Градиент давления — ► pressure gradient Изменение давления, отнесенное к единице длины … Нефтегазовая микроэнциклопедия

ГРАДИЕНТ ДАВЛЕНИЯ — понижение давления, отнесенное к единице длины пути … Словарь по гидрогеологии и инженерной геологии

градиент давления бурового раствора — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN drilling mud pressure gradientmud pressure gradient … Справочник технического переводчика

градиент давления паров — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN vapor pressure gradient … Справочник технического переводчика

градиент давления при гидроразрыве — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN fracture gradient … Справочник технического переводчика

градиент давления при движении жидкости — (в пласте или в подъёмных трубах) [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN flowing pressure gradient … Справочник технического переводчика

градиент давления в кардиологии — разность давления крови в каких либо двух отделах сердечно сосудистой системы, непосредственно сообщающихся между собой … Большой медицинский словарь

Источник

Градиент давления: что это такое и как рассчитывается?

Содержание:

Например, в бассейне, наполненном водой, есть градиент давления положительный в вертикальном направлении вниз, потому что давление увеличивается с глубиной. С каждым метр (или сантиметр, фут, дюйм) глубины давление линейно растет.

Однако во всех точках, расположенных на одном уровне, давление одинаковое. Следовательно, в пуле градиент давления равен нулю (нулю) в горизонтальном направлении.

В нефтяной промышленности очень важен градиент давления. Если давление на дне отверстия выше, чем на поверхности, масло будет выходить легко. В противном случае перепад давления пришлось бы создавать искусственно, путем перекачки или нагнетания пара.

Жидкости и их интересные свойства

Это обстоятельство принимается во внимание, наблюдая, что твердые тела сохраняют фиксированную форму, в то время как жидкости, как уже упоминалось, принимают в большей или меньшей степени форму контейнера, в котором они находятся.

Газы и жидкости считаются жидкостями, потому что они ведут себя подобным образом. Газ полностью расширяется, чтобы заполнить емкость.

С другой стороны, жидкости не достигают такого количества, поскольку они имеют определенный объем. Разница в том, что жидкости можно считать несжимаемыйа газов нет.

Это последнее ограничение важно, поскольку в действительности почти любое вещество может вести себя как жидкость при определенных условиях экстремальной температуры и давления.

В недрах земли, где условия можно считать экстремальными, камни, которые на поверхности были бы твердыми, тают в магма и они могут вытекать на поверхность в виде лавы.

Расчет давления

Чтобы найти давление, оказываемое столбом воды или любой другой жидкости на дно контейнера, считается, что жидкость имеет следующие характеристики:

Столб жидкости в этих условиях оказывает прочность на дне контейнера, в котором он находится. Эта сила эквивалентна его весу W:

Теперь плотность жидкости, которая, как объяснено выше, является частным между ее массой м и его объем V, это:

Плотность обычно измеряется в килограммах / кубических метрах (кг / м 3 ) или фунтов на галлон (ppg)

Подставляя выражение для плотности в уравнение веса, получаем:

Гидростатическое давление п Он определяется как отношение силы, действующей перпендикулярно к поверхности, и ее площади A:

Давление = Сила / Площадь

Подставляя объем столба жидкости V = площадь основания x высота столба = A.z, уравнение давления принимает следующий вид:

Приведенное выше уравнение показывает, что более плотные жидкости будут оказывать большее давление. И давление тем больше, чем меньше поверхность, на которую оно действует.

Подставляя объем столба жидкости V = площадь основания x высота столба = A.z, уравнение давления упрощается:

Приведенное выше уравнение показывает, что более плотные жидкости будут оказывать большее давление. И давление тем больше, чем меньше поверхность, на которую оно действует.

Как рассчитать градиент давления?

Уравнение P = ρgz указывает, что давление п столба жидкости линейно увеличивается с глубиной z. Поэтому вариант ΔP давления, будет связано с изменением глубины Δz следующим образом:

Определение новой величины, называемой удельным весом жидкости γ, определяемой по формуле:

Что переписывается как:

Это градиент давления.Теперь мы видим, что в статических условиях градиент давления жидкости постоянен и равен ее удельному весу.

Единицы градиента давления такие же, как и удельный вес, но могут быть переписаны как Паскаль / метр в Международной системе. Теперь можно визуализировать интерпретацию градиента как изменение давления на единицу длины, как определено в начале.

Удельный вес воды при температуре 20 ºC составляет 9,8 килопаскаль / м или 9800 Па / м. Это означает, что:

«На каждый метр, опущенный в толщу воды, давление увеличивается на 9800 Па».

Коэффициент преобразования плотности

Значения плотности и удельного веса любой жидкости были определены экспериментально для различных условий температуры и давления. Они доступны в таблицах значений.

Чтобы найти числовое значение градиента давления между различными системами единиц, необходимо использовать коэффициенты преобразования, которые ведут от плотности непосредственно к градиенту.

Коэффициент преобразования 0,052 используется в нефтяной промышленности для перехода от плотности в фунтах на галлон к градиенту давления в фунтах на квадратный дюйм / фут. Таким образом, градиент давления рассчитывается следующим образом:

GP = коэффициент преобразования x плотность = 0,052 x плотность_ppg

Например, для пресной воды градиент давления составляет 0,433 фунта на квадратный дюйм / фут. Значение 0,052 получается с помощью куба, стороны которого измеряют 1 фут. Для наполнения этого ведра требуется 7,48 галлона жидкости.

Сейчас в 1 футе 2 там 144 квадратных дюйма, поэтому в 1 футе 3 на каждый фут длины будет 144 квадратных дюйма. Деление 7,48 / 144 = 0,051944, что примерно равно 0,052.

Например, если у вас есть жидкость с плотностью 13,3 фунта на галлон, ее градиент давления будет: 13,3 x 0,052 фунта на квадратный дюйм / фут = 0,6916 фунта на квадратный дюйм / фут.

Источник

Градиенты давления

Статические градиенты. В большинстве природных резервуаров статический градиент изменения пластового давления с глубиной составляет в среднем 45 фунт/кв. дюйм/100 фут (0,1 атм/м). Это характерно для воды, содержащей растворенные соли в количестве 55 000 ч. на млн. (5,5%) (см. Приложение, табл. А-1). Иногда наблюдаются градиенты давления, достигающие 100 фунт/кв. дюйм/100 фут (0,23 атм/м). По-видимому, такие градиенты обусловлены уже не весом столба воды, а весом перекрывающих горных пород, для которых градиент давления равен примерно этой величине.

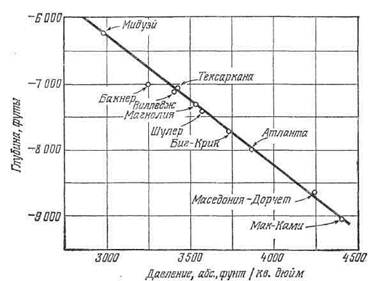
Несколько примеров пластовых давлений, замеренных по десяти нефтяным залежам в продуктивных известняках Смаковер в южном Арканзасе, приведены на фиг. 9-2. Градиенты давления составляют в среднем 52 фунт/кв. дюйм/100 фут. Плотность пластовых вод формации Смаковер равна 1,22, что соответствует градиенту 52 фунт/кв. дюйм/100 фут и расположению потенциометрического уровня приблизительно у земной поверхности. Средний статический градиент давления для провинции Галф-Кост в США обычно принимается равным 46,5 фунт/кв. дюйм/100 фут. Но известны градиенты, превышающие эту величину. Пластовые давления в группе залежей Большая Офисина в восточной Венесуэле показаны на фиг. 9-15.

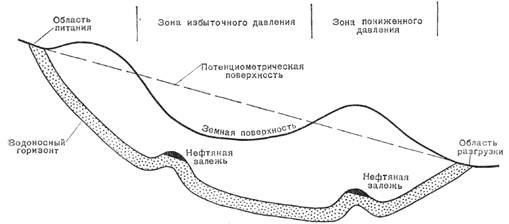
Фиг. 9-3. Соотношение потенциометрической поверхности и поверхности земли. Расстояние между областями питания и разгрузки измеряется сотнями миль. Пластовые условия гидродинамические: вода движется из области питания к области разгрузки в направлении наклона потенциометрической поверхности.

¹Термин «пьезометрическая поверхность» уже давно употребляется в гидрогеологии. В тех случаях, когда имеется в виду энергия воды, Хабберт применяет термин «потенциометрическая поверхность» [43, стр. 1973-1974].

Потенциометрическая поверхность водоносного горизонта представляет собой поверхность, связывающую все точки гидростатического напора (высота, до которой поднимается вода относительно нулевой плоскости отсчета), и является мерой потенциальной энергии воды во всех точках кровли этого горизонта независимо от его гипсометрического положения. Обычно пьезометрическая поверхность соответствует расчетной потенциометрической поверхности только в том случае, если при построении последней учитывалась плотность воды в каждой конкретной точке замера давления. Пьезометрическая поверхность соответствует поверхности, которая может быть определена с помощью серии скважин, рассматриваемых в качестве манометров, если потенциометрическая поверхность уже рассчитана и можно достаточно объективно судить о том, как плотность флюида может быть использована для преобразования величины давления флюида в величину его потенциала.

Связь между давлением флюида и потенциалом флюида по Хабберту может быть выражена формулой

Разделив оба отношения на g, получим

Это отношение часто используетсядля расчета величины потенциала флюида, символизируемого потенциометрической поверхностью напора h, по известной величине давления флюида. Поскольку ρg равно градиенту р, для этого расчета используется статический градиент давления соответствующего флюида, но при этом имеется один минус, касающийся плотности флюида, так как в реальных геологических условиях плотность воды в любой гидрогеологической системе никогда не бывает постоянной. Однако практически ошибка может быть значительно уменьшена, если все величины гидростатического давления в любой данной гидрогеологической системе превращать в величины потенциометрической поверхности исходя из предположения о постоянной плотности всех вод этой системы. В том случае, если известны различия в плотности флюида между любыми двумя точками замера давления флюида, в расчеты могут быть внесены соответствующие поправки.

Давление измеряется усилием, приходящимся на единицу площади. В единой гидравлической системе давление флюида может быть различным на каждом конкретном уровне, даже если движение жидкости отсутствует, т.е. в гидростатических условиях. Если имеется разница в давлении флюида на одном и том же уровне, то различается и потенциал флюида, т.е. существуют гидродинамические условия. Величины давлений флюида, замеренные на разных уровнях, могут быть скорректированы до величины давления, которая должна была бы быть на одном уровне, с помощью соответствующего данному флюиду статического градиента давления ρg. Если различия в величинах давлений флюида тем не менее остаются и после такой корректировки, следует говорить о преобладании в этой системе гидродинамических условий.

Региональные и локальные гидродинамические исследования водоносных горизонтов обычно проводятся в границах потенциометрической поверхности, рассчитанной по данным замеров давлений флюидов во всех доступных точках перспективного района. Результаты этих замеров изображаются в виде карты потенциометрической поверхности, изолинии которой соединяют точки равных значений потенциала флюида или равных высот потенциометрической поверхности. Поток воды в этой системе изображается как движение в направлении, перпендикулярном изолиниям потенциометрической поверхности, от площадей с высоким положением последней к площадям с низким ее положением. Другими словами, вода в водоносном горизонте течет вниз по наклону потенциометрической поверхности.

При использовании данных о давлении для поисков нефти (при условии, что имеются два или более замера давления флюида) интерпретация этих данных зависит от того, сделаны ли замеры в одном и том же пласте, в одной и той же скважине, на одной и той же глубине, в одно и то же или в различное время. Например, замеры статического пластового давления часто производятся в одной и той же скважине, но в различное время с целью получения сведений для определения промысловых характеристик пласта, в частности количества добытой нефти, приходящегося на одну атмосферу падения пластового давления. Если замеры давления флюида производятся на различных горизонтах, но в одной скважине и, главное, в одно и то же время, и при этом оказывается, что высоты расчетной потенциометрической поверхности одинаковы для всех замеренных пластовых давлений, то такие горизонты на данном участке считаются находящимися в гидростатическом равновесии. Если же высоты потенциометрической поверхности различны для разных горизонтов, на которых произведены замеры давления, то между пластами существует гидродинамический градиент; и, кроме того, если между ними имеются проницаемые зоны, например по сбросам, тектоническим трещинам или поверхностям несогласий, то пластовые флюиды будут двигаться вдоль этих зон от пластов с относительно высокими значениями потенциала флюида к пластам с более низкими его значениями.

Фиг. 9-4. Три водоносных пласта А, В и С в одной скважине, характеризующиеся различными потенциометрическими поверхностями А, В и С.

Стрелками показано направление движения воды в случае сообщающихся пластов.

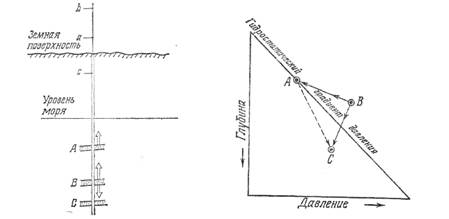
Фиг. 9-5. Диаграмма распределения давления флюида в водоносных пластах А, В и С с учетом гидростатического градиента давления.

Диаграмма показывает различие в величинах потенциалов флюидов между сообщающихся пластов. В случае сообщаемости пластов вода будет двигаться от пласта В к пластам А и С и от пласта А к пласту С.

Подобным же образом если данные регионального изучения изменения давления в каком-либо одном водоносном пласте свидетельствуют о том, что потенциометрическая поверхность горизонтальна, то такая система находится в гидродинамическом равновесии; в случае наклонной потенциометрической поверхности имеет место гидродинамический градиент, и флюиды будут двигаться по проницаемым зонам от участков с высокими значениями потенциала к участкам с низкими значениями последнего (фиг. 9-4 и 9-5). Можно провести аналогию с системой городского водопровода: потенциометрическая поверхность горизонтальна, если все краны закрыты, но если хотя бы один кран откроют, давление в этой точке понижается, устанавливается градиент гидравлического потенциала и вода движется в сторону открытого крана.

В седиментационном бассейне можно выделить два основных вида гидродинамической обстановки: 1) различие в гидравлических потенциалах внутри одного водоносного пласта, обусловливающее движение воды в пласте вдоль поверхностей напластования; 2) различие в потенциалах флюидов между разными пластами в разрезе, обусловливающее движение флюида вверх или вниз по проницаемым зонам, секущим поверхности напластования, от пластов с относительно высоким потенциалом флюида к пластам с более низким его значением. В зависимости от конкретных геологических условий в пластовой системе, содержащей залежи нефти или газа, могут проявляться одна или обе гидродинамических обстановки. Доказательством наличия градиента потенциала флюида в одном пласте является наклонная потенциометрическая поверхность. О существовании вертикального градиента потенциала флюида между различными пластами свидетельствует различие в высоте потенциометрической поверхности одного

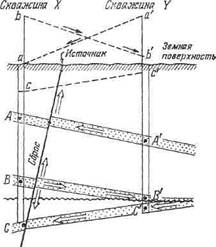
Фиг. 9-6. Схематическое изображение соотношения давлений флюида и потенциометрических уровней в двух скважинах X и Y, вскрывших одни и те же водоносные пласты.

пласта относительно другого (пласты находятся на различной глубине в пределах одной и той же части разреза) (фиг. 9-4). Можно также указать на два основных вида градиентов потенциала флюида внутри пласта-коллектора: 1) естественные градиенты, характерные для данного региона, и 2) искусственные градиенты, образовавшиеся в эксплуатирующейся скважине или в залежи в результате извлечения флюидов и соответствующего снижения пластового давления (фиг. 9-5).

Градиент гидравлического потенциала конкретного пласта или системы пластов обычно определяется как изменение высоты потенциометрической поверхности (bb?) на данном горизонтальном расстоянии (XY) (фиг. 9-6). Кроме того, он может быть выражен как величина снижения напора, или потенциометрической поверхности, на единицу расстояния (например, 25 футов на 1 милю между точками X и Y на фиг. 9-6). Гидродинамические соотношения между различными пластами в геологическом разрезе (А, В, С на фиг. 9-4 и 9-6) изображаются различными уровнями (а, b и с) потенциометрических поверхностей систем на одном и том же участке.

При извлечении флюидов из скважины вокруг нее образуется зона пониженного пластового давления. Эта зона распространяется во всех направлениях от скважины, создавая локальный градиент потенциала флюида, направленный к скважине. Это по существу искусственная локальная потенциометрическая поверхность, наклоненная в сторону скважины. Зона пониженного потенциала флюида вокруг одиночной скважины сообщается с зонами низкого пластового давления, окружающими другие скважины. В конечном счете это приводит к тому, что пластовое давление по всей залежи становится более низким, чем начальное пластовое давление. Снижение пластового давления распространяется от залежи на различные расстояния и с различной скоростью в зависимости от характера пластовых флюидов и проницаемости коллекторов.

Заметный градиент давления, возникающий при разработке залежи, которая приурочена к замкнутым резервуарам¹ (например, к изолированной линзе или участку пористой породы, окруженной относительно непроницаемыми отложениями), практически не обнаруживается за пределами проницаемой зоны. Однако чаще залежь располагается не в замкнутой, а в ограниченной системе и связана с широко распространенным по площади водоносным горизонтом. Градиент давления, обусловленный разработкой такой залежи, может наблюдаться на значительном расстоянии. Так, например, в залежах, приуроченных к оолитам Рейнолдс (свиты Смаковер) в южном Арканзасе или к известнякам Асмари в Иране, зоны пониженного пластового давления распространяются на несколько километров от работающих скважин. Очень характерен в этом отношении бассейн Ист-Тексас (или Тайлер), где эффект от снижения пластового давления на месторождении Ист-Тексас отчетливо прослеживается на всей площади бассейна, на расстоянии 70 миль или более от месторождения [7]. Снижение пластового давления в бассейне Ист-Тексас показано на фиг. 10-17.

Параметры пластового давления в двух скважинах, вскрывших несколько водоносных пластов, в схематическом виде показаны на фиг. 9-6. Для того чтобы определить точное направление и скорость движения воды, необходимо располагать не менее чем тремя контрольными точками (скважинами). Гидродинамические условия, изображенные на фиг. 9-6, безусловно, существовали в течение геологического времени, но постоянно менялись величины градиентов гидравлического потенциала и направление движения воды, что обусловливалось эрозией, деформациями и осадконакоплением. Различия в потенциале флюидов, существующие между пластами и внутри них, образуют комплекс гидродинамических условий, обычный для большинства осадочных бассейнов.

Источник

Пластовое давление

Обычно прогноз пластового давления основан на предположении о том, что оно изменяется строго пропорционально глубине скважины, причем коэффициент пропорциональности называют часто коэффициентом (индексом) аномальности k_a:

l_пл– глубина расположения пласта (в наклонно направленных скважинах вместо глубины по стволу берут вертикальную проекцию ствола на данной глубине.), м.

Тогда получается, что для определения пластового давления вполне достаточно знать только величину k_a для различных интервалов бурения. Обычно принимают, что для некоторого интервала бурения k_a – величина постоянная. Однако то обстоятельство, что для всех интервалов бурения расчет пластового давления ведут с помощью формулы (1.1), представляющей собой уравнение прямой, исходящей их начала координат, означает, во-первых, что линии пластовых давлений являются отрезками прямых, а во-вторых, продолжения этих отрезков образуют лучи, исходящие из устья скважины.

На рис. 1 показаны четыре луча, соответствующие разным значениям индекса пластового давления k_a . У луча 0а оно минимально, а у луча 0g – максимально. На глубине L_а изменяется индекс аномальности k_a , и линия скачком переходит на другой луч и так далее. В результате образуется ломаная линия 0abcdefghi, включающая горизонтальные участки ab, cd, ef, hg. Известны случаи локального роста пластового давления на некотором интервале бурения (по сравнению с соседними пластами) с последующим возвратом на прежний (или близкий к прежнему) уровень давлений. На рис. 1. этому соответствует участок efghi.

Величина q_пл, в строгом смысле, характеризует изменение пластового давления в пределах некоторого интервала бурения или пласта, приходящееся на единицу длины (как правило, это 1 м) и вычисляется по формуле:

где p_пл2 и p_пл1 – пластовые давления соответственно на глубинах L₂и L₁ (например, в подошве и кровле пласта).

Если обнаружится, что для любых двух глубин в пределах данного интервала бурения (пласта) величина q_пл постоянна (одна и та же), то это будет означать, что пластовое давление изменяется по линейному закону.

Но это совсем не означает, что продолжение прямой пройдет точно через устье скважины, как это имеет место на рис. 1. И здесь возможны варианты (рис. 2):

1. Участок 0′ a отражает изменение р_пл в верхней части разреза, насыщенной пресными или маломинерализованными водами со статическим уровнем пластовой воды в скважине, как правило, ниже уровня земли («сухой» отрезок 0-0′). Предположим теперь, что каким-то образом удалось замерить пластовые давления в точках a’ и a. Вычисляя теперь по формуле (1.1) коэффициенты аномальности k_a (при известных давлениях и глубинах), мы бы получили разные величины k_a для указанных глубин (прямые 0а и 0а’ не совпадают). Но выше мы только что доказали, что наличие линейной связи между давлением и глубиной автоматически означает постоянство градиента давления. В этих условиях применение формулы (1.1) с коэффициентом k_a, найденным по глубине L_a, приведет к завышению р_пл для всех глубин, меньших L_a.

2. Если продолжение прямой линии пластового давления (прямая 0 с на рис. 2) проходит через устье скважины, то имеет место частный случай постоянства k_a и q_пл на всем интервале бурения. При этом расчеты по формуле (1.1) будут тоже точными.

4. Продуктивная толща газовых месторождений и некоторых, например, Прикаспийских, имеют большую протяженность (несколько сотен метров), и отдельные проницаемые участки (коллектора) имеют между собой гидродинамическую связь в вертикальном направлении. Такие залежи месторождений называют массивными. Пластовое давление в пределах продуктивных пластов распределяется не пропорционально глубине, а в соответствии с плотностью флюида в пластовых условиях. В продуктивной части газового месторождения – в зависимости от плотности сжатого газа, в нефтяных – от плотности нефти в пластовых условиях. На рис. 2 прямая fg иллюстрирует распределение давления в газовой залежи. Считается, что в подошве залежи давление близко к давлению в водоносных пластах на соответствующей глубине, зато в кровле оно существенно больше «нормального» и воспринимается как АВПД. Для таких случаев прогнозный расчет по формуле (1.1) в принципе возможен только для подошвы залежи. Что касается давления в кровле, то оно определяется по формулам (соответственно для газа и нефти):

где p_пд и p_кр – пластовое давление в подошве и в кровле пласта;

r_н— плотность нефти в пластовых условиях;

Для многопластовых месторождений нефти, когда каждый нефтеносный пласт может рассматриваться как самостоятельная залежь малой мощности (единицы метров) с собственным водонефтяным контактом, в пределах нефтеносной части распределение тоже будет по закону, описанному формулой (1.4). Однако, в связи с малой мощностью пластов, описанным эффектом аномальности в кровле пренебрегают, и пластовые давления определяют либо по формуле (1.1), либо через градиент давления q_пл, если известно давление для одной из глубин в пределах рассматриваемого интервала бурения.

На линии пластовых давлений выделяются горизонтальные площадки, что свидетельствует о скачкообразном изменении пластового давления при достижении определенных глубин. Если подходить формально, то получается, что в одной точке пласта существуют два давления, что абсурдно. Все дело в том, что в реалии переход от одного давления к другому происходит не сразу, а на некотором, относительно коротком (в несколько метров) интервале. Вследствие малости интервала переход на новое давление показывают в виде ступенек.

Существует еще один способ оценки пластового давления и его изменения, суть которого сводится к определению эквивалентной плотности жидкости, которая, находясь (условно) в скважине от рассматриваемой точки пласта на глубине L_i до устья, создает гидростатическое давление, численно равное пластовому на данной глубине:

Понятие «эквивалентная плотность» применяется не только к пластовому давлению, но используется и для описания всех других давлений, представленных в ТПД: гидростатического, давления гидроразрыва и горного. Вычисляются они по формуле (1.5) с заменой числителя на значения соответствующих давлений.

Предположим, что в кровле пласта на глубине 2000 м пластовое давление оказалось равным 21,6 МПа, а в подошве, на глубине 2500 м – 27 МПа.

— коэффициент аномальности k_a = 21,6*10 6 / (1000*9,81*2000)=1,1 (на глубине 2000 м),

— коэффициент аномальности k_a = 27*10 6 / (1000*9,81*2500)=1,1 (на глубине 2500 м),

— градиент пластового давления в интервале 2000-2500 м:
q_пл = (27-21,6)/ (2500-2000) = 0,0108 МПа/м,

Приближенный, но весьма распространенный метод прогнозирования пластового давления, предполагает использование формулы (1.1).

Более строгий метод расчета пластового давления предусматривает точное знание давления на одной из глубин в пределах пласта (интервала бурения), например, прямым измерением глубинными манометрами, и расчет давления для других глубин с использованием величины градиента давления(По определению пластовое давление – фактор природный, и его величина в принципе не может зависеть от человека. Однако бывает пластовое давление «рукотворным». Например, в результате добычи нефти имеет место уменьшение давления в продуктивных пластах. При закачке в пласт жидкости или газа для восстановления пластовой энергии оно, наоборот, увеличивается и может превысить первоначальное давление. ).

Источник