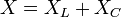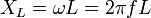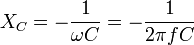в чем измеряется емкостное сопротивление

Ёмкостное сопротивление

Реактивное сопротивление определяет мнимую часть импеданса:

В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:

Индуктивное сопротивление (X_L) обусловлено возникновением ЭДС самоиндукции. Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока:

Ёмкостное сопротивление (X_C). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока:

См. также

Полезное

Смотреть что такое «Ёмкостное сопротивление» в других словарях:

ёмкостное сопротивление — величина, характеризующая сопротивление, оказываемое переменному току электрической ёмкостью цепи (или её участка). Ёмкостное сопротивление синусоидальному току Хс = 1/ωС, где ω угловая частота, С ёмкость. Измеряется в омах. * * * ЕМКОСТНОЕ… … Энциклопедический словарь

ёмкостное сопротивление — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN capacitancecondensancecapacitive reactancecapacity… … Справочник технического переводчика

ёмкостное сопротивление — talpinė varža statusas T sritis fizika atitikmenys: angl. capacitance; capacity reactance; capacitive reactance vok. kapazitiver Widerstand, m rus. ёмкостное сопротивление, n pranc. capacitance, f; réactance capacitive, f … Fizikos terminų žodynas

Ёмкостное сопротивление — см.Сопротивление ёмкостное … Большая советская энциклопедия

ЁМКОСТНОЕ СОПРОТИВЛЕНИЕ — см. Сопротивление ёмкостное … Большой энциклопедический политехнический словарь

ЁМКОСТНОЕ СОПРОТИВЛЕНИЕ — физ. величина, характеризующая сопротивление, оказываемое переменному току электрич. ёмкостью цепи (или её участка). Ё.с. синусоидальному току Хс = 1/w С, где w угловая частота, С ёмкость. Измеряется в омах … Естествознание. Энциклопедический словарь

зарядное ёмкостное сопротивление — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN charge capacitance … Справочник технического переводчика

СОПРОТИВЛЕНИЕ — (1) аэродинамическое (лобовое) сила, с которой газ действует на движущееся в нём тело. Оно всегда направлено в сторону, противоположную скорости движения тела, и является одной из составляющих аэродинамической силы; (2) С. гидравлическое… … Большая политехническая энциклопедия

ёмкостное реактивное сопротивление — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN capacitive reactance … Справочник технического переводчика

Сопротивление реактивное — электрическое, величина, характеризующая сопротивление, оказываемое переменному току электрической ёмкостью (См. Электрическая ёмкость) и Индуктивностью цепи (её участка); измеряется в омах (См. Омаха). В случае синусоидального тока при… … Большая советская энциклопедия

Источник

Емкостное и индуктивное сопротивление в цепи

Разность потенциалов между точками электрической цепи порождает ток, который представляет собой упорядоченное движение электронов под действием электрополя. В том случае, когда напряжение постоянное, в цепи будет только активное сопротивление. Если же напряжение переменное, то появляется еще реактивное сопротивление, которое определяется индуктивностью и емкостью компонентов используемой схемы.

Виды сопротивления и их особенности

Если в цепи постоянное напряжение, то, зная её сопротивление, можно узнать силу тока при помощи закона Ома. Он говорит о том, что сила тока пропорциональна напряжению, которое является его причиной. Коэффициент пропорциональности представляет обычное сопротивление. Его принято называть активным.

Если напряжение является постоянным, то сопротивление будет только активным. Его значение определяет, сколько энергии электрического поля преобразовано в тепло, то есть, безвозвратно утрачено. Поэтому при работе с кабелями СИП-3 1×50, СИП-2 3×70 и другими нужно помнить, что потери энергии из-за активного сопротивления могут быть значительными.

Более распространено использование переменного тока. Он возникает под воздействием напряжения, циклически изменяющегося по синусоидальному закону. Такой ток порождает реактивное сопротивление, которое дополняет действие активного. Существует две разновидности реактивного сопротивления различной природы — на основе индуктивности или емкости. Их отличительной особенностью является то, что они способствуют не трате электроэнергии, а преобразованию её в другую форму.

Нужно учитывать, что применение различных видов кабелей связано не только с наличием активного сопротивления, но и реактивного. Например, кабели СИП-3 1×50, СИП-2 3×70, АС-95 могут использоваться в электросетях и с активным, и индуктивным, и емкостным сопротивлениями.

Чтобы понять, что собой представляет индуктивное сопротивление, можно представить цепь, в которой имеется катушка, подключённая к источнику переменного тока. Как известно, напряжение меняется по синусоидальному закону. При этих изменениях катушка будет создавать магнитное поле, которое будет, в частности, влиять на текущий через него ток. Согласно природе магнитного поля, при уменьшении тока магнитное поле способствует его увеличению, а при усилении наблюдается противоположный эффект. Кроме того, цепь переменного тока с активным сопротивлением тратит энергию на выделение тепла.

На практике речь идёт о действии индуктивного сопротивления, обеспечивающего сдвиг фазы между током и напряжением. Движение зарядов создаёт поле, которое в свою очередь препятствует изменению тока. Такое сопротивление присутствует не только в катушках, но и, например, при использовании кабеля СИП-2 3×70.

Емкостное сопротивление имеет другую природу. Для объяснения следует рассмотреть цепь, состоящую из источника переменного тока и конденсатора. Последний представляет собой деталь, в которой две поверхности параллельны друг другу и не имеют непосредственного электрического контакта.

При использовании постоянного тока на обкладках конденсатора накапливаются заряды: на одной — положительный, а на второй — отрицательный. Электрополе за счет накопленного заряда представляет собой источник, противодействующий току. Поэтому конденсатор в цепи постоянного тока является бесконечно большим сопротивлением. Ток не проходит сквозь диэлектрик, разделяющий обкладки конденсатора.

В цепи переменного тока конденсатор циклически заряжается и разряжается, обеспечивая движение электрозарядов. Данный процесс в цепи переменного тока с активным и реактивным сопротивлением будет происходить с опозданием относительно синусоидального изменения напряжения. Таким образом, конденсатор представляет собой конечное сопротивление, получившее название емкостного.

Разница между емкостным и индуктивным сопротивлением заключается в том, что через индуктивную катушку постоянный ток протекает, а при использовании конденсатора пройти не может. Однако переменный ток в обеих цепях может течь без каких-либо проблем.

Полное сопротивление

На практике необходимо учитывать как активное, так и индуктивное и емкостное сопротивления. Это особенно важно при выборе компонентов для электрических сетей. Например, активное, емкостное и индуктивное сопротивления кабелей СИП-3 зависят от их номинального сечения. Поэтому при создании электролинии следует выбрать правильный диаметр проводника, чтобы в будущем не возникало аварийных ситуаций.

При наличии нескольких разновидностей сопротивления возникает понятие полного сопротивления. Графически его представляют в виде прямоугольного треугольника. Длина одного его катета представляет величину активного сопротивления, а другого — разницу между значениями индуктивного и емкостного сопротивлений. Полное сопротивление в этом случае будет измеряться гипотенузой. В соответствии с теоремой Пифагора она определяется по следующей формуле:

Пример использования

Если в сети необходимо регулировать силу тока, удобно использовать реостат (переменное сопротивление). При использовании этой детали, действие которой основано на омическом сопротивлении, можно видеть, как расходуется энергия на нагрев. Таким образом, его можно включать в цепь с активным сопротивлением и индуктивностью с целью регулировки обоих видов сопротивления.

Если вместо реостата используется катушка с изменяемыми параметрами, она позволяет легко произвести регулировку и при этом избежать нагрева. Такое решение особенно удобно, если используется электрическая цепь со значительным напряжением. Когда присутствует активное, емкостное и индуктивное сопротивление, регулировать можно любое из них.

При использовании проводов или обычных радиодеталей в электрической цепи на самом деле измеряется и индуктивное, и ёмкостное сопротивления. Каждое из них зависит от частоты тока, а также от физических и геометрических особенностей используемых схем. Например, провод АС 50 или АС 70 может иметь индуктивное сопротивление в пределах 0.392–0.435 Ом/км. У А 50 аналогичная величина составляет от 0.297 до 0.468 Ом/км. Изолированный кабель АВБбШв 4х240 характеризируется величиной сопротивления всего 0.077 Ом/км.

При выборе проводов необходимо учитывать особенности соответствующих марок. Например, в наименованиях АС 95, АС 120 и других цифра указывает толщину проводов, от которой зависят их электрические свойства. При работе с изолированными самонесущими кабелями СИП-2 3×70, СИП-3 1×50, СИП-3 1×70, СИП-3 1×95, СИП-3 1×120 нужно помнить, что их характеристики зависят не только от физических показателей, но и от номинального напряжения.

Видео по теме

Источник

Емкостное сопротивление

Использование ёмкости в цепи постоянного тока знакомо каждому электронщику. В этом случае работа детали описывается сравнительно простыми физическими законами. Несколько сложнее дела обстоят с переменным током, ведь при таком применении ёмкости уже возникает необходимость учитывать реактивное сопротивление.

Формула ёмкостного сопротивления

При подаче на обкладки конденсатора переменного напряжения ток через этот элемент первоначально стремится к максимальному значению. По мере заряда прибора он постепенно снижается. В то же время вольтаж ведёт себя иначе, т.е. плавно возрастает от нуля до максимального значения.

Подобный эффект вызван ёмкостным сопротивлением. Оно зависит как от строения самого электронного прибора, так и от характеристик поданного на него переменного напряжения.

Обратите внимание! Ёмкость элемента можно узнать по маркировке, имеющейся на его корпусе. Если она нечитаемая или стёрлась, то эта величина определяется с помощью мультиметра. Он должен быть с функцией замера ёмкости (прим. DT9208A).

Векторное представление ёмкости

Для простоты понимания процессов, происходящих в конденсаторе под действием источника переменного тока, удобно воспользоваться векторным представлением ёмкости.

В начальный момент зарядки конденсатора потенциал U на его обкладках равен нулю (точка a). В то же время ток I имеет своё максимальное значение (точка b). На этом этапе уже заметно отставание. Ток начинает снижаться со своей пиковой величины (участок bd). Напряжение в этот момент ещё не выросло и только подбирается к своему максимуму (ac).

Подобное отражается и на диаграмме справа. В момент, когда вольтаж U имеет своё наименьшее значение (e), ток I только начинает переходить в отрицательную область (f).

Емкостное сопротивление

Ёмкостное, оно же реактивное, сопротивление принципиально зависит от частоты напряжения. Данная связь хорошо видна на графике, приведённом ниже. Чем выше частота, тем меньше реактивное сопротивление. Очевидно это и из вышеприведённой формулы. Переменная f (частота) стоит в знаменателе. Поэтому с её увеличением Xc будет уменьшаться.

Емкость в цепи переменного тока

При подаче на конденсатор постоянного напряжения он постепенно зарядится до максимальной разности потенциалов на его обкладках. После этого ток через электронный компонент прекратится и, не считая ничтожной утечки, будет равняться нулю. Поэтому в цепи постоянного тока конденсатор имеет огромное сопротивление. При расчетах его величину принимают равной бесконечности.

Реактивное сопротивление имеет вполне исчисляемое значение. Его можно измерить с помощью осциллографа, генератора и постоянного резистора. Для этого потребуется собрать схему. В ней конденсатор образует с резистором делитель напряжения. С помощью осциллографа будет измеряться потенциал, который образуется на выводах ёмкости.

Для данной схемы вычисления имеют следующий вид.

Здесь:

Важно! Электрический кабель также обладает ёмкостью. Поэтому после снятия напряжения на нём остаётся некоторый заряд. Данное явление опасно для человека, особенно, если проводник до отключения находился под потенциалом 1000 В и выше.

Единицы измерения

Для правильного проведения всех расчетов важно понимать, какие величины в них используются, и что они обозначают:

Пример расчета емкостного сопротивления

Для расчета понадобится большинство из перечисленных физических величин. Они обозначены на схеме и в качестве примера имеют следующие значения:

Реактив будет рассчитываться по вышеописанной формуле:

В таком случае сопротивление конденсатора в цепи переменного тока равно 96,5 кОм. Если расписать все вычисления, то получится следующее.

Сама по себе формула не вызывает сложности. Однако для проведения вычислений необходимы знания школьного курса алгебры, т.е. умение работать со степенями, дробями и прочими алгоритмами математики. На практике имеет смысл немного схитрить. Чтобы каждый раз не городить сложные вычисления, можно воспользоваться одним из онлайн калькуляторов из сети Интернет. Подобные ресурсы позволяют произвести комплексный расчёт и выяснить некоторые другие параметры цепи.

Свойства ёмкостей

Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C.

Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU. Здесь U – напряжение источника питания.

Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.

Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.

Видео

Источник

Что такое емкостное реактивное сопротивление и как его рассчитать?

Содержание:

В емкостное сопротивление Это сопротивление, которое конденсатор, регулирующий поток заряда в цепи переменного тока, противодействует прохождению тока.

В цепи, состоящей из конденсатора и активируемой источником переменного тока, емкостное реактивное сопротивление X может быть определено_C следующим образом:

Емкостное реактивное сопротивление зависит от обратной частоты, поэтому на высоких частотах оно обычно мало, а на низких частотах реактивное сопротивление велико.

Пока идет заряд, через конденсатор устанавливаются переменное напряжение и ток, амплитуды или максимальные значения которых обозначаются соответственно как V_C и я_C, связаны емкостным сопротивлением аналогично закону Ома:

В конденсаторе напряжение на 90 ° отстает от тока или ток на 90 ° опережает ток, как вы предпочитаете. В любом случае частота такая же.

Когда X_C очень большой, ток имеет тенденцию быть маленьким, и значение X стремится к бесконечности_C, конденсатор ведет себя как разомкнутая цепь и ток равен нулю.

Как рассчитать емкостное реактивное сопротивление

Рассмотрим пример расчета емкостного реактивного сопротивления: предположим, что конденсатор 6 мкФ подключен к розетке переменного тока с напряжением 40 В и частотой F 60 Гц.

Для определения емкостного реактивного сопротивления используется определение, данное в начале. Угловая частота ω определяется как:

Затем этот результат подставляется в определение:

Теперь посмотрим на амплитуду тока, циркулирующего в цепи. Поскольку источник предлагает напряжение амплитудой V_C = 40 В, мы используем соотношение между емкостным реактивным сопротивлением, током и напряжением для вычисления амплитуды тока или максимального тока:

я_C = V_C / ИКС_C = 40 В / 442,1 Ом = 0,09047 А = 90,5 м А.

Если частота становится очень большой, емкостное реактивное сопротивление становится небольшим, но если частота становится равной 0 и у нас есть постоянный ток, реактивное сопротивление стремится к бесконечности.

Ток и напряжение на конденсаторе

Когда конденсатор подключен к источнику переменного тока, когда он колеблется и меняет свою полярность, конденсатор испытывает переменные заряды и разряды.

Для частоты 60 Гц, такой как в примере, напряжение положительное 60 раз в секунду и отрицательное еще 60 раз в секунду.

По мере увеличения напряжения он толкает ток в одном направлении, но если конденсатор разряжается, он производит ток в противоположном направлении, противоположном первому.

C = q / V → q (t) = CV = CV_м сен ωt

И имея нагрузку как функцию времени, у нас будет ток, который является производной от этого:

Но синус и косинус связаны соотношением: cos α = sin (α + π / 2), следовательно:

я_C(t) = CV_м ω sin (ωt + π / 2) = I_C грех (ωt + π / 2)

Как видите, существует разница в 90º опережения тока по отношению к напряжению, как было сказано в начале.

В описании этого типа схем используется понятие фазор, который очень похож на вектор и позволяет представить любую переменную величину, такую ​​как ток, напряжение или импеданс, на комплексной плоскости.

На следующем рисунке справа показаны векторы напряжения и тока в конденсаторе, которые образуют между ними угол 90º, который представляет собой разность фаз между ними.

Слева соответствующие графики, разных амплитуд, но одинаковой частоты. Со временем ток опережает напряжение, и когда он максимален, ток равен нулю, а когда напряжение равно нулю, ток максимален, но с обратной полярностью.

Комплексное сопротивление конденсатора

Фактически, импеданс цепи определяется как отношение напряжения к току:

Для конденсатора или конденсатора его импеданс определяется отношением:

Z_C = v (t) / i (t) = V_C sin ωt / I_C грех (ωt + π / 2)

Импеданс последовательной RC-цепи

Импеданс цепи переменного тока с резисторами, конденсаторами и катушками индуктивности также может быть представлен биномиально следующим образом:

Если в цепи последовательно соединены резистор и конденсатор, их полное сопротивление составляет:

Например, в схеме, показанной ниже, источник имеет вид:

Учитывая, что ω = 120π, импеданс равен:

Приложения с емкостным реактивным сопротивлением

Фильтры верхних частот, фильтры нижних частот, мостовые схемы для измерения емкости и индуктивности и схемы фазового сдвига являются одними из основных применений схем, которые содержат емкостные реактивные сопротивления в сочетании с индуктивностями и электрическими сопротивлениями.

В стереосистемах некоторые динамики поставляются с отдельными динамиками. вуфер (больше) для низких частот и твитер или небольшой рог для высоких частот. Это улучшает производительность и качество звука.

В них используются конденсаторы, которые предотвращают попадание низких частот в высокочастотный динамик, а в низкочастотном динамике добавлен индуктор, чтобы избежать высокочастотных сигналов, поскольку индуктивность имеет реактивное сопротивление, пропорциональное частоте: X_L = 2πfL.

Источник

Емкостное сопротивление.

Емкостное сопротивление в цепи переменного тока — это та часть сопротивления, которая создается конденсатором, включенным в цепь переменного тока (при пренебрежимо малой емкости подводящих прово­дов).

Для получения формулы емкостного сопротивления определим, как меняется сила тока в цепи, содержащей только конденсатор.

.

Напряжение на обкладках конденсатора u = φ₁ – φ₂ = q/C равно напряже­нию на входе цепи, поэтому

Для силы тока, которая определяется как производная заряда q по времени, из (q = C U_m cos ωt) полу­чим:

Между напряжением и силой тока в цепи с конденсатором наблюдается сдвиг фаз на π/2 (), причем ток опережает напряжение. Когда конденсатор разряжается (напряжение на нем равно нулю), ток максима­лен.

Амплитуда силы тока равна

.

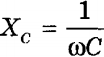
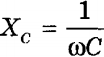
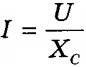
называется емкостным сопротивлением. Если вместо амплитуд силы тока и напряжения в (I_m = U_m Cω) использовать их действующие значения, то, учитывая , получим:

.

Это означает, что действующие значения силы тока и напряжения на конденсаторе связаны так же, как и сила постоянного тока и напряжение согласно закону Ома, причем роль активного сопротивления R играет емкостное сопротивление Х_с.

Чем больше емкость конденсатора и частота напряжения, тем меньше емкостное сопротивле­ние и тем больше ток перезарядки.

Благодаря сдвигу фаз между током и напряжением в среднем за период не происходит ни накопления энергии на конденсаторе, ни ее диссипации (рассеяния). За четверть периода, когда конденсатор заряжается до максимального значения, на нем происходит накопление энергии электрического поля; в следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.

Источник