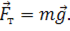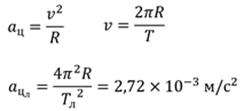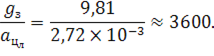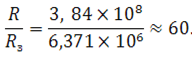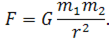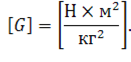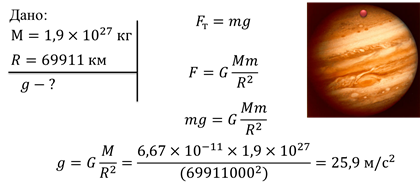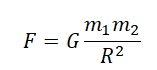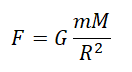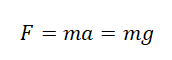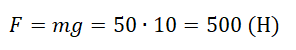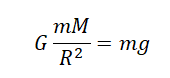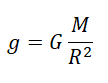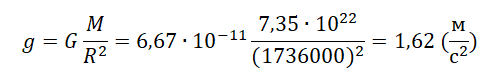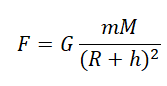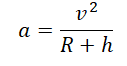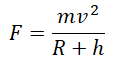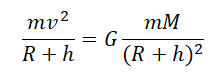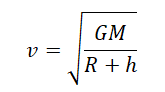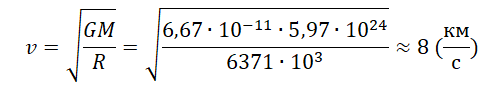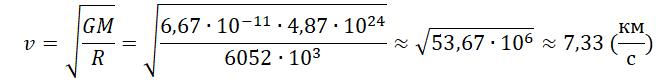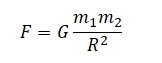что нужно сделать чтобы уменьшить силу тяготения между двумя телами

Явление тяготения. Сила тяжести

Содержание

Мы рассмотрели множество примеров с различными телами, когда они взаимодействуют друг с другом. Мы рассматривали совсем маленькие предметы, физические тела больших размеров.

Но одно очень большое физическое тело, с которым каждый из нас взаимодействует каждый день, мы оставили на рассмотрение в этом уроке. Имя этому телу — наша планета Земля.

Закон всемирного тяготения

Начнем с самого простого. Если нет ветра, капли дождя падают вертикально вниз на землю. Если мы отпустим камень из руки, то он тоже упадет на землю.

Если пнуть мяч, то он не полетит в прямом направлении вечно. Его траекторией будет кривая линия (рисунок 1). В конце движения он все равно окажется на земле.

Рисунок 1. Траектория полета мяча

Искусственные спутники запускаю вверх, но они не улетают по прямой в неизведанные космические пространства. Они движутся вокруг Земли.

Все эти тела участвуют в некотором взаимодействии, на них действует сила — сила притяжения к Земле.

К Земле притягивается все, что на ней находится: люди, океаны, наша атмосфера, дома, животные.

Кроме этого, можно сказать, что она притягивает все тела — например, Луну, Солнце, другие небесные объекты. Но взаимодействие не бывает односторонним, значит, и Земля притягивается ко всем этим телам.

Рассмотрим Луну и Землю. Взаимодействие этих небесных тел (их взаимное притяжение) вызывает приливы и отливы вод на Земле (рисунок 4). Дважды в сутки огромные массы воды поднимаются и опускаются по всей планете.

Вся наша Солнечная система взаимодействует подобным образом. Планеты притягиваются к Солнцу и друг к другу (рисунок 5).

Рисунок 5. Солнечная система и время оборота планет вокруг солнца.

Всемирное тяготение — это притяжение всех тел Вселенной друг к другу.

Открытие закона всемирного тяготения

Закон всемирного тяготения был открыт Ньютоном, когда ему было 23 года (в 1666 году), но опубликован позже — в 1687 году. Согласно этому закону,

Силы притяжения между телами тем больше, чем больше массы этих тел. Силы притяжения между телами уменьшаются, если увеличивается растояние между ними.

Сила тяжести

Для всех нас, живущих на планете Земля, наиболее важное значение имеет сила притяжения всех тел к Земле, а не наоборот. Так мы подошли к определению силы тяжести:

Cила тяжести — это сила, с которой Земля притягивает к себе тело.

Сила тяжести:

Земля имеет не идеальную форму шара, а немного сплюснута у полюсов (рисунок 7).

Рисунок 7. Схематическое изображение формы Земного шара.

Из-за этого сила тяжести на полюсах немного больше, чем на других участках планеты. По той же причине сила тяжести у подножья горы будет больше, чем на ее вершине.

Также имеется связь с массой тела:

Cила тяжести прямо пропорциональна массе рассматриваемого тела.

Т.е., если мы возьмем два тела с разными массами, то:

Источник

Силы всемирного тяготения. Закон всемирного тяготения

Урок 17. Физика 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Силы всемирного тяготения. Закон всемирного тяготения»

Вы уже знакомы с явлением всемирного тяготения из курса девятого класса. Так же мы говорили о том, что все тела, обладающие массой, притягиваются друг к другу. Из второго закона Ньютона следует, что любая равнодействующая сила равна произведению массы тела и ускорения, сообщаемого этой силой: .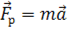

Так, например, сила тяжести равна произведению массы тела и ускорения свободного падения:

Но, как мы уже выяснили, ускорение свободного падения не зависит от массы тела, из чего можно сделать вывод, что гравитационные силы сообщают ускорение, которое не зависит от массы тела!

Это поразительное свойство можно объяснить только тем, что гравитационные силы пропорциональны массе тела, на которое они действуют. А теперь, вспомним третий закон Ньютона: тела действуют друг на друга с силами, равными по модулю, направленными по одной прямой в противоположных направлениях: .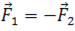

В частности, если Земля действует на Луну с некоторой силой, то и Луна должна действовать на Землю с этой силой. Значит, гравитационная сила, возникающая между двумя телами пропорциональна массам обоих тел.

Рассмотрим теперь ускорение, с которым двигается Луна. Напомним, что любое криволинейное движение является ускоренным. Движение Луны вокруг Земли хорошо известно людям: период обращения Луны вокруг Земли составляет примерно 27,3 земных суток, а средний радиус орбиты Луны составляет 384 тыс. километров. Исходя из этого, мы можем подсчитать центростремительное ускорение Луны:

Если мы сравним теперь получившуюся величину с ускорением свободного падения на Земле, то убедимся, что ускорение Луны примерно в 3600 раз меньше, чем ускорение свободного падения на Земле:

А теперь, сравним радиус Земли с расстоянием между Землёй и Луной:

Оказывается, что радиус Земли примерно в 60 раз меньше, чем расстояние между Землей и Луной. Заметим, что 60 2 — это 3600. Из этого можно заключить, что сила тяготения между двумя телами уменьшается пропорционально квадрату расстояния между этими телами.

Исходя из всего вышеперечисленного, формулировка закона всемирного тяготения такова: сила взаимного притяжения двух тел прямо пропорциональна произведению их масс и обратно пропорционально квадрату расстояния между ними.

Необходимо отметить, что если тела не являются материальными точками, то за расстояние между ними принимается расстояние между центрами тяжести этих тел. В формуле мы видим коэффициент пропорциональности, который называется гравитационной постоянной. Гравитационная постоянная численно равна силе притяжения между двумя материальными точками массами 1 кг, если расстояние между ними составляет 1 метр.

Гравитационная постоянная является очень важной константой, поскольку именно с её помощью люди смогли вычислить массу Земли, Луны, Солнца и так далее. Но как вычислить саму гравитационную постоянную?

Впервые гравитационная постоянная была измерена Генри Кавендишем в 1798 году. С помощью крутильных весов, ему удалось определить значение гравитационной постоянной достаточно точно (оно почти совпадает с принятым сегодня значением).

Крутильные весы представляют собой следующую установку: на тонкой упругой нити подвешено лёгкое коромысло с двумя шарами на концах. Рядом закреплены два значительно более тяжёлых шара (в эксперименте Кавендиша легкие шары имели массу 775 г, а тяжёлые – 49,5 кг). В результате гравитационного взаимодействия, коромысло поворачивалось и закручивало нить. Зная упругие свойства нити, Кавендишу удалось измерить силу притяжения. Поскольку, массы шаров ему были известны, так же, как и расстояние между ними, Кавендиш смог вычислить гравитационную постоянную.

Необходимо отметить, что закон всемирного тяготения дает точный результат, в трех случаях:

1) Если оба тела имеют форму шара и являются однородными.

2) Если размеры тел ничтожно малы, по сравнению с расстоянием между ними.

3) Если одно из тел обладает формой шара и его размеры многократно больше размеров второго тела любой формы.

Примеры решения задач.

Задача 1. Юпитер обладает массой 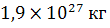и радиусом 69 911 км. Определите ускорение свободного падения на Юпитере.

Поскольку закон всемирного тяготения является одним из универсальных законов природы, он одинаково выполняется для всех тел, имеющих массу. Рассмотрим произвольное тело (масса и размеры которого ничтожно малы по сравнению с массой и размерами Юпитера).

Задача 2. Вычислите, на какой высоте над поверхностью Земли должен находиться геостационарный спутник.

На первый взгляд может показаться, что в задаче нет исходных данных. Но если мы внимательно рассмотрим ситуацию, то убедимся, что некоторые данные у нас есть. В первую очередь, — это период обращения спутника: разумеется, он должен быть равен периоду обращения Земли вокруг своей оси. И самое главное: спутник должен двигаться с постоянной скоростью, поскольку Земля тоже двигается с постоянной скоростью.

Необходимо отметить, что в задачах мы принимали орбиты планет за окружности для упрощения расчетов. В действительности, планеты Солнечной системы двигаются по эллиптическим орбитам, поэтому, когда мы говорим о расстоянии от планеты до Солнца, мы имеем ввиду средний радиус её орбиты.

Источник

Закон всемирного тяготения. Сила тяжести

1. Силы, с которыми все тела притягиваются друг к другу, называют силами всемирного тяготения или гравитационными силами.

Закон всемирного тяготения был установлен Ньютоном, и он утверждает, что тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними.

где ​ \( m_1 \) ​ и ​ \( m_2 \) ​ — массы тел, ​ \( r \) ​ — расстояние между телами, ​ \( G \) ​ — постоянная всемирного тяготения или гравитационная постоянная.

Значение гравитационной постоянной свидетельствует о том, что силы тяготения между телами малы. Они становятся заметными при больших значениях масс взаимодействующих тел. Например, притяжение шарика к Земле можно наблюдать без специальных приборов, а притяжение Земли к такому же шарику мы не можем наблюдать непосредственно.

Закон всемирного тяготения справедлив для тел, размерами которых можно пренебречь по сравнению с расстоянием между ними (для материальных точек). Закон применим также к шарам, в этом случае расстоянием между телами является расстояние между центрами шаров.

2. Все тела притягиваются к Земле. Силу притяжения тела к Земле называют силой тяжести ​ \( (F_т) \) ​.

По второму закону Ньютона сила равна произведению массы тела и ускорения, с которым оно движется под действием этой силы. Ускорение, с которым движется тело под действием силы тяжести, называется ускорением свободного падения и обозначается буквой ​ \( g \) ​. Ускорение свободного падения не зависит от массы тела. Соответственно, сила тяжести рассчитывается но формуле: ​ \( F_т=mg \) ​.

Полученная формула позволяет вычислить ускорение свободного падения тела, находящегося на поверхности Земли. Она наглядно показывает, что значение ускорения свободного падения зависит от расстояния тела до центра Земли. Именно поэтому оно на экваторе больше, чем на полюсах.

По этой формуле можно вычислить ускорение свободного падения на любой планете, подставив вместо массы Земли массу соответствующей планеты, а вместо радиуса
Земли радиус планеты.

5. Пользуясь законом всемирного тяготения, можно вычислить скорость, которую необходимо сообщить телу для того, чтобы оно стало спутником Земли. Эта скорость
называется первой космической скоростью.

Центростремительное ускорение ​ \( a \) ​ спутнику массой ​ \( m \) ​ обеспечивает сила тяготения ​ \( F_т \) ​, которая по второму закону Ньютона равна ​ \( F_т=ma \) ​. Сила тяготения ​ \( F_т=G\frac \) ​, центростремительное ускорение равно ​ \( a=\frac \) ​, где ​ \( v \) ​ — линейная скорость спутника, ​ \( R \) ​ — радиус Земли. Откуда следует: ​ \( G\frac=m\cdot\frac \) ​ или ​ \( g=\frac \) ​. Отсюда ​ \( v=\sqrt \) ​, т.е. первая космическая скорость равна 7,9 км/с. Первый в мире искусственный спутник Земли был запущен в СССР в 1957 г.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Сила тяготения между двумя телами уменьшится в 2 раза, если массу каждого тела

1) увеличить в √2 раз
2) уменьшить в √2 раз
3) увеличить в 2 раза
4) уменьшить в 2 раза

2. Массу каждого из двух однородных шаров увеличили в 4 раза. Расстояние между ними тоже увеличили в 4 раза. Сила тяготения между ними

1) увеличилась в 64 раза
2) увеличилась в 16 раз
3) увеличилась в 4 раза
4) не изменилась

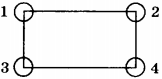
3. В вершинах прямоугольника расположены тела одинаковой массы. Со стороны какого тела на тело 1 действует наибольшая сила?

1) со стороны тела 2
2) со стороны тела 3
3) со стороны тела 4
4) со стороны всех тел одинаковая

4. Закон всемирного тяготения справедлив

A. Для всех тел
Б. Для однородных шаров
B. Для материальных точек

1) А
2) только Б
3) только В
4) и А, и Б

5. На ящик массой 5 кг, лежащий на полу лифта, движущегося с ускорением ​ \( a \) ​ вертикально вниз, действует сила тяжести

1) равная 50 Н
2) большая 50 Н
3) меньшая 50 Н
4) равная 5 Н

1) ​ \( F_э=F_м \) ​
2) \( F_э>F_м \) ​
3) \( F_э ​
4) ответ может быть любым в зависимости от массы тел

7. Сила тяжести, действующая на космонавта на поверхности Луны,

1) больше силы тяжести, действующей на него на поверхности Земли
2) меньше силы тяжести, действующей на него на поверхности Земли
3) равна силе тяжести, действующей на него на поверхности Земли
4) больше силы тяжести, действующей на него на поверхности Земли на экваторе, и меньше силы тяжести, действующей на него, на поверхности Земли на полюсе

8. Сила тяжести, действующая на тело, зависит от

А. Географической широты местности
Б. Скорости падения тела на поверхность Земли

1) только А
2) только Б
3) ни А, ни Б
4) и А, и Б

9. Какое(-ие) из утверждений верно(-ы)?

Сила тяжести, действующая на тело у поверхности некоторой планеты, зависит от

А. Массы планеты.
Б. Массы тела.

1) только А
2) только Б
3) ни А, ни Б
4) и А, и Б

10. Первая космическая скорость зависит

A. От радиуса планеты
Б. От массы планеты
B. От массы спутника

1) только А
2) только Б
3) только А и Б
4) А, Б, В

11. Установите соответствие между физической величиной (левый столбец) и формулой, выражающей её взаимосвязь с другими величинами (правый столбец). В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Сила тяжести
Б. Ускорение свободного падения на поверхности Земли
B. Закон всемирного тяготения

12. Среди приведённых утверждений выберите два правильных и запишите их номера в таблицу

1) Гравитационная постоянная показывает, с какой силой притягиваются друг к другу два тела массой 1 кг.
2) Значение силы тяжести, действующей на тело, зависит от скорости его движения.
3) Ускорение свободного падения зависит от массы и радиуса планеты.
4) При увеличении расстояния между телами в 3 раза сила тяготения между ними уменьшается в 9 раз.
5) Изменение массы одного из взаимодействующих тел не влияет на значение силы тяготения.

Часть 2

13. Человек на Земле притягивается к ней с силой 700 Н. С какой силой он притягивался бы к Марсу, находясь на его поверхности, если радиус Марса в 2 раза меньше радиуса Земли, а масса в 10 раз меньше, чем масса Земли?

Источник

Гравитационные силы. Закон всемирного тяготения.

теория по физике 🧲 динамика

Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.

Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.

Закон всемирного тяготения

Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.

F — сила всемирного тяготения, m₁и m₂ — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10 –11 Н ∙ м 2 /кг 2 ).

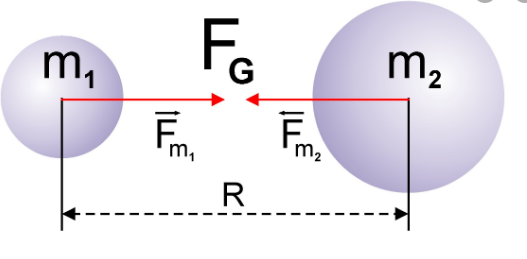
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.

Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m₁= 1 кг и m₂= 1 кг, то F = G.

Сила тяжести

Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.

Сила тяжести — сила, с которой Земля притягивает к себе тела.

Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.

Расчет силы тяжести на Земле

Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:

Вывод формулы ускорения свободного падения

Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.

Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.

Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:

Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:

Формула расчета ускорения свободного падения

Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.

Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙10 22 кг.

Переведем километры в метры: 1736 км = 1736000 м.

Первая космическая скорость

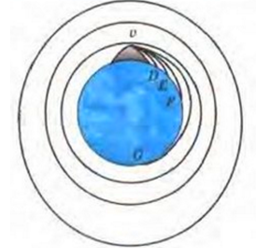
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.

Определение Первая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.

Вывод формулы первой космической скорости

Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:

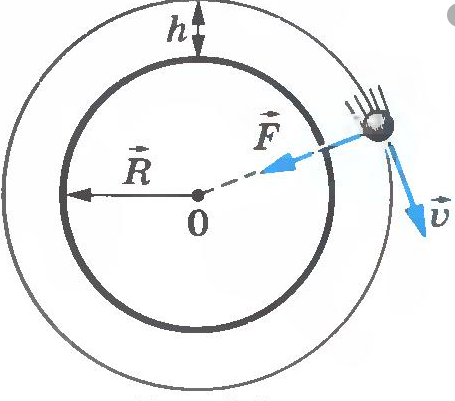
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.

Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:

Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:

Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:

Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:

Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.

Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:

8 км/с — первая космическая скорость Земли.

Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙10 24 кг, а ее радиус равен 6052 км.

Алгоритм решения

Решение

Запишем исходные данные:

Запишем закон всемирного тяготения:

Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m₁ и m₂.

R₂ больше R₁ втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 3 2 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?

Источник