что больше по объему вода или лед
Что тяжелее: 1 литр воды или 1 литр льда
Соотношение объема и массы воды
Литр – это единица объема для жидких веществ. Литрами допустимо измерять также сыпучие вещества с достаточно мелкой фракцией. Для прочих твердых тел используют понятие кубический метр (дециметр, сантиметр). Определение термина и понятия литра было сформулировано Генеральной конференцией по мерам и весам в 1901 году. Определение звучит следующим образом: 1 литр – это объем одного килограмма чистой пресной воды при атмосферном давлении 760 мм ртутного столба и температуре +3,98оС. При этой температуре вода достигает наибольшей плотности.
Перейдя температурный порог в +3,98оС, плотность воды снова начинает уменьшаться, и при +8оС опять достигает тех же значений, что и при нуле.
Что тяжелее?
Если в какой-либо сосуд налить, к примеру, 1 кг воды, она будет иметь объем, равный одному литру. Если вы подвергните эту воду заморозке, то при той же массе в 1 кг, вода, замерзая, будет стремиться занять больше места в сосуде. Закрытый сосуд, ограниченный емкостью 1 кв. дм (1 литр), лед разорвет. Получается, что при одинаковой массе жидкой и замороженной воды, лед будет иметь больший объем, что нарушит первоначальное условие.
Если поставить на заморозку литровую пластиковую бутылку с 1 000 мл воды (1 литр), то в процессе отвердения из нее выльется примерно 80 мл воды. А чтобы получить 1 литр льда, достаточно заморозить 920 мл воды.
Заморозить и восстановить
Сегодня все труднее встретить чистую природную воду. Особенно в условиях города, где она, прежде чем попасть в квартиру, фильтруется, хлорируется, подвергается другим видам физической и химической обработки. Чистая вода становится дефицитом, стоимость добываемой воды из артезианских скважин растет. Однако вода, оказывается, восстанавливает свою изначальную структуру и энергетику после заморозки – она очищается. Поэтому: пейте талую воду! Не зря на нее так хорошо реагируют весной все растения и с удовольствием пьют животные.
Парадокс закона Архимеда
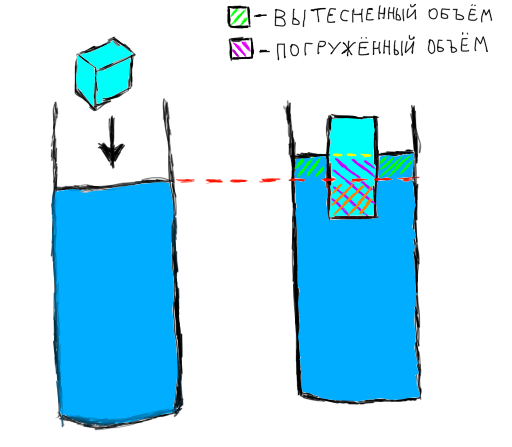
Существуют две разные формулировки закона Архимеда: «выталкивающая сила равна весу жидкости в объёме погружённой части тела» и «выталкивающая сила равна весу вытесненной телом жидкости». На первый взгляд кажется, что эти формулировки эквивалентны, ведь объём вытесненной жидкости равен погружённому объёму. Но на самом деле это абсолютно неверно. Чтобы понять почему, взглянем на рисунок.
В стакан с водой мы опускаем кубик льда. Красной пунктирной линией обозначен старый уровень воды, жёлтой — новый. Зелёным заштрихован вытесненный объём, фиолетовым — погружённый, а оранжевым — тот объём льда, который погружён ниже красной линии. Поскольку вода несжимаема, ясно, что зелёный объём равен оранжевому. Но как видно из рисунка, оранжевый объём является частью фиолетового. Фиолетовый объём намного больше оранжевого. А поскольку оранжевый равен зелёному, фиолетовый больше зелёного. Это означает, что погружённый объём больше вытесненного.
Нетрудно понять, что объём погружённой части всегда будет больше или равен вытесненному. Ведь вытесненный объём равен тому объёму тела, который погружён ниже старого уровня жидкости, а он, в свою очередь, является частью общего погружённого объёма. Значит, вытесненный объём будет равен погружённому только в том случае, когда вся погружённая часть тела находится ниже старого уровня жидкости.
Но если погружённый и вытесненный объёмы не равны, возникает вопрос: какая же формулировка закона Архимеда верна? Чтобы ответить на него, вспомним, как выводится закон Архимеда.
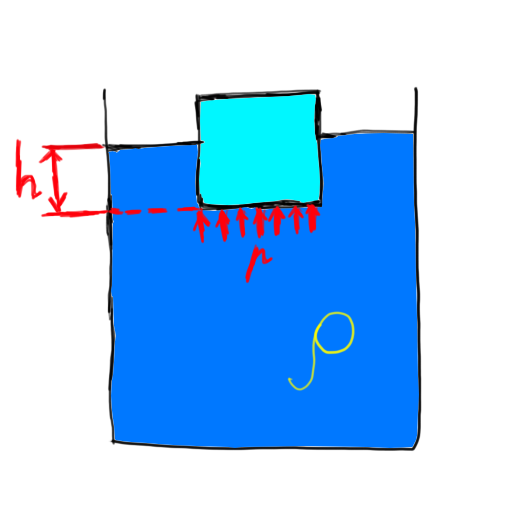
Вернёмся ко льду в воде. Пусть он погружён на глубину h. В любой точке на этой глубине давление равно ρgh, где ρ — плотность жидкости, g — ускорение свободного падения, h — глубина. По закону Паскаля давление передаётся без изменений во всех направлениях. Таким образом, это давление жидкость оказывает на нижнюю грань кубика. Пусть её площадь равна S. Тогда сила давления на нижнюю грань кубика равна ρghS = ρgV, где V — объём погружённой части кубика (V = hS). Эта сила и есть выталкивающая. Таким образом, получается, что выталкивающая сила равна весу жидкости в объёме погружённой части тела, а вовсе не весу вытесненной жидкости.
Из всего вышесказанного также следует, что водоизмещение корабля совсем не обязательно будет равно его массе (если под водоизмещением мы подразумеваем массу вытесненной воды). Поскольку корабль не тонет, сила тяжести, действующая на него, равна силе архимеда:
mg = ρgV (m — масса корабля, g — ускорение свободного падения, ρ — плотность воды, V — погружённый объём).
Разделив это уравнение на g, получим
Обозначим объём вытесненной воды как Vвыт. Поскольку
ρVвыт ≤ ρV ⇔ ρVвыт ≤ m.
Но ρVвыт — это масса вытесненной воды, то есть, водоизмещение. Следовательно, водоизмещение меньше или равно массе корабля.
Ситуацию, когда водоизмещение меньше массы корабля, проще всего наблюдать, когда корабль плавает в тесном доке. Даже если масса воды в доке меньше массы корабля, он всё равно не будет касаться дна, несмотря на то, что не будет вытеснять воду с массой, равной своей.
заполни изначально стакан до краев, чтобы жидкость выливалась, и не еби мозг
Но если погружённый и вытесненный объёмы не равны,
Кто тебе сказал, что они не равны?
«Поскольку вода несжимаема, ясно, что зелёный объём равен оранжевому. Но как видно из рисунка, оранжевый объём является частью фиолетового. Фиолетовый объём намного больше оранжевого. А поскольку оранжевый равен зелёному, фиолетовый больше зелёного. Это означает, что погружённый объём больше вытесненного.»
Зачем ты написал эту хуйню?
Или ты правда в нее веришь?
Даже если масса воды в доке меньше массы корабля, он всё равно не будет касаться дна
«На первый взгляд кажется, что эти формулировки эквивалентны, ведь объём вытесненной жидкости равен погружённому объёму. Но на самом деле это абсолютно неверно. Чтобы понять почему, взглянем на рисунок.»
Если я нарисую автора с тремя руками, это будет доказательством наличия у него трех рук?
Неправильно уже первое утверждение «Поскольку вода несжимаема, ясно, что зелёный объём равен оранжевому». Дальше эту куету не читал.
Тело, впихнутое в воду, выпирает на свободу с силой выпертой воды телом, впихнутым туды.)
Иначе получится неприятный казус. Вода должна подняться, но при поднятии ещё больший объём погружается воду, значит вода должна ещё чуть подняться; и так до того момента, пока весь предмет не будет погружён в воду! Приходим к выводу, что ни один предмет не может всплыть из воды, что неверно!
Вот ещё более интересная задачка про погружаемое тело и высоту столба жидкости вокруг него, Вам однозначно погравится https://zen.yandex.ru/media/id/5e4f1d8670d2aa13e1bf7948/oche.
Проблема Больцмановского мозга и как она появилась
Текстовая версия видео:
Допустим, что время движется именно в сторону максимальной энтропии. Что это значит для нашей Вселенной? Опять же, многое указывает на то, что в будущем наступит состояние с максимальной энтропией, термодинамическое равновесие, когда все частицы барионной материи будут двигаться почти с одинаковой скоростью. А Вселенная мало того, что и так огромная, так еще и расширяется, в общем скорость этих самых частиц будет практически нулевая, будет колебаться возле абсолютного нуля. Такое состояние еще называют «Тепловой смертью Вселенной». Существуют аргументы против того, что это произойдет, но опять же, не буду начинать все перечислять.
Итак, в чем же проблема с энтропией и вечной Вселенной. Если бы Вселенная была вечной, то мы бы не наблюдали таких объектов как, например, звезды, туманности и тем более жизнь, ведь все температуры уравнялись бы, было бы состояние термодинамического равновесия, то есть максимальной энтропии.
Так вот, в конце 19 века стоял вопрос. Если Вселенная вечна, то почему она не находится в состоянии с максимальной энтропией, почему не все имеет одинаковую температуру, ведь неизбежно температуры должны были уравняться за бесконечный промежуток времени, что следовало из законов термодинамики.
Получается такой вот парадокс. Подумайте, как бы вы его разрешили.
Некий физик, Людвиг Больцман, предложил аж два решения и надо отдать ему должное – додуматься до такого в те времена (19 век) было необычайно умно.
Что же он предложил? Одно из решений заключалось в том, что Вселенная начала свое существование с состояния с низкой энтропией. Другими словами, она была очень горячей в недалеком прошлом и понемногу постепенно охлаждается.
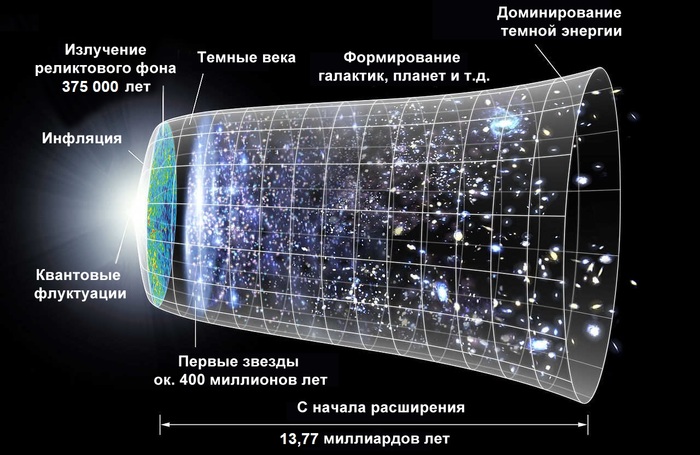
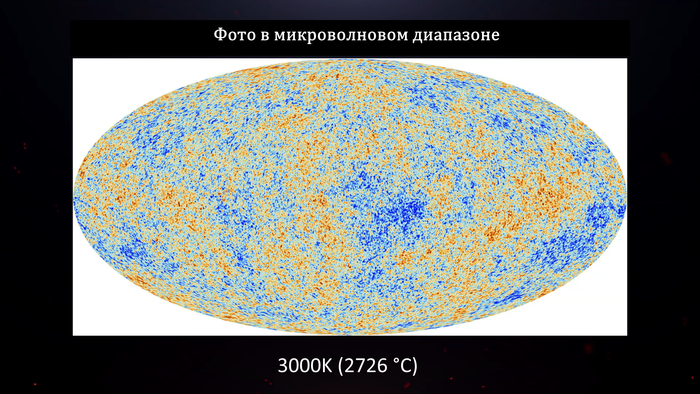
Сейчас мы знаем, что именно так и было – Вселенная начала свое существования с очень низкой энтропией относительно недавно по сравнению с вечностью – примерно 13.8 миллиардов лет назад (это один из нетривиальных способов доказать Большой Взрыв). У нас даже есть фотографии той горячей эпохи.
Вот, например, фотография Вселенной примерно 400 тысяч лет после Большого Взрыва, когда она имела температуру около 3000 кельвинов (2726 °C). Казалось бы, что тогда наоборот термодинамическое равновесие было больше и соответственно энтропия больше, чем сейчас, но это не так. Второе объяснение Больцмана более необычное. Он предположил, что да, Вселенная существовала вечно и в ней вечно было термодинамическое равновесие, максимальная энтропия, в общем практически везде одинаковая, холодная Вселенная. Но Больцман пошел дальше и высказал гипотезу, что атомы, наполняющие эту Вселенную, в ходе хаотических флуктуаций случайно собрались таким невероятным образом, что в итоге в одной части Вселенной случайно появилось все то, что мы наблюдаем: планеты, звезды, туманности и так далее.
Казалось бы, что это полнейший бред, такого произойти не может. Но на самом деле нет. В вечной Вселенной такое событие произойдет бесконечное количество раз – из хаоса появятся структуры любой сложности, но чем более сложная структура, тем меньшая вероятность ее случайного появления. Просто бесконечность, да и вообще очень большие или очень маленькие числа для нас неинтуитивны.
Существует очень известная «теорема о бесконечных обезьянах», которая утверждает, что абстрактная обезьяна, ударяя случайным образом по клавишам пишущей машинки в течение неограниченно долгого времени, рано или поздно напечатает любой наперёд заданный текст.
В общем, если событие имеет сколь угодно малую вероятность, то за бесконечное количество времени это событие произойдет с вероятностью 100%. Приведу еще примеры. Если на бильярдном столе шары будут двигаться вечно, то за бесконечное количество времени они случайно хотя бы на момент создадут любой возможный узор из шаров, хотя понятно, что такие события маловероятны, большинство времени они будут просто хаотически двигаться.
Представим, что мы заключили газ в какой-то коробке, можете представить, что ваша комната и воздух в ней являются такой коробкой с газом и что эта система (система из газа в коробке), является изолированной – то есть не может обмениваться энергией с внешним миром.
Газ в коробке будет стремиться к максимальной энтропии, к термодинамическому равновесию, что выглядит как хаотическое равномерное движение всех частиц, но существует шанс, мизерный, что газ случайно соберется на одной стороне коробки. Энтропия такой системы уменьшится, но ненадолго, газ опять быстро достигнет термодинамического равновесия.
За бесконечное количество времени произойдет бесконечное количество таких событий – газ соберется в одной стороне коробки бесконечное количество раз. Вообще, любая конфигурация, не нарушающая закон сохранения импульса и энергии произойдет в этой коробке, газ соберется в одну точку, сформирует различные фигуры, даже случайно напишет слово «энтропия» и случайно создаст микромодель, например, Солнечной Системы.
Парадокс действительно можно было решить этим объяснением, но позже физики пришли к следующим выводам: вероятность появления видимой Вселенной в результате случайных тепловых флуктуаций чрезвычайно мала, речь идет о вероятностях порядка 1 до Числа Грэма. Чем менее сложная структура и с чем меньшего количества частиц она состоит, тем большая вероятность появления такой структуры в вечной Вселенной. Звезда в результате хаотического движения частиц появится с большей вероятностью, чем галактика. Планета появится с большей вероятностью, чем звезда.
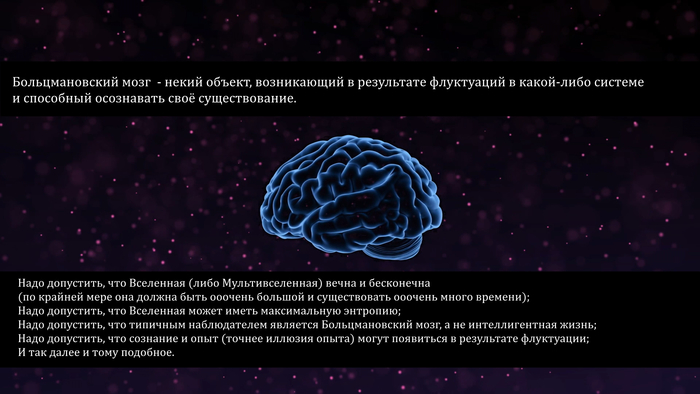
Человек появится с большей вероятностью, чем планета. Мозг, осознающий себя появится с большей вероятностью, чем человек. Согласно такой логике, с большей вероятностью ты, осознающий себя, на самом деле являешься просто случайно собравшимся мозгом из частиц во Вселенной с термодинамическим равновесием, причем все твои воспоминания — это иллюзия, они тоже появились случайно. Все, что ты видишь, знаешь и наблюдаешь – тоже иллюзия, на самом деле ты лишь мозг случайно появившийся посреди хаоса.
Сейчас в научных кругах проблему Больцмановских мозгов часто называют, в переводе на русский, «ложный наблюдатель» (freak observer), обычно это касается работ посвященных Мультивселенной. Если существует бесконечное число Вселенных, ну или очень большое число Вселенных с различными физическими законами, то математически большая вероятность, что во всем мультуме Вселенных больше мозгов Больцмана, а не обычных живых существ, и осознающий себя ты, опять же, с большей вероятностью это Больцмановский мозг, а не тот, кем себя представляешь.
Так в конце концов, все-таки я – Больцмановский мозг и все мои воспоминания поддельны, или нет?
Это нельзя проверить, это не наука, в это можно верить, либо не верить, а это уже решать вам. Добавлю еще, что некоторые ученые называют проблему Больцмановского мозга глупостями, а некоторые постоянно придумывают способы как-то ее опровергнуть и привести аргументы против, да и вообще проблема Больцмановского мозга возникает только при некоторых допущениях. Не вижу смысла более глубоко раскрывать эту тему, все основное я рассказала. Моей целью было предоставить пищу для размышлений. Приятного аппетита =)
Гидростатистический парадокс)
Это глобальное потепление во всем виновато
Что такое «парадокс убитого дедушки» и как его решить
Путешествия во времени — одна из самых интригующих фантастических концепций. Но она вызывает много вопросов — как у физиков, так и у философов, — а также может привести к разным парадоксам. «Парадокс убитого дедушки» — один из них.
Концепция путешествий во времени вовсю используется в литературе и кино, вне зависимости от жанров. Зачастую в центре всех таких историй — изменения, внесенные путешественником в события прошлого, которые приводят к настоящим катастрофам в будущем. Стоит вспомнить хотя бы рассказ Рэя Брэдбери «И грянул гром».
Эта дилемма, также известная как «парадокс убитого дедушки», представляет собой главное возражение физиков и философов против путешествий во времени: возможное нарушение причинности. И хотя путешествия во времени пока лишь спекуляция, вероятные результаты нарушения принципа причинности и того, как природа может их предотвратить, — предметы горячих споров среди таких ученых, как Стивен Хокинг и Кип Торн.
Что такое «парадокс убитого дедушки»
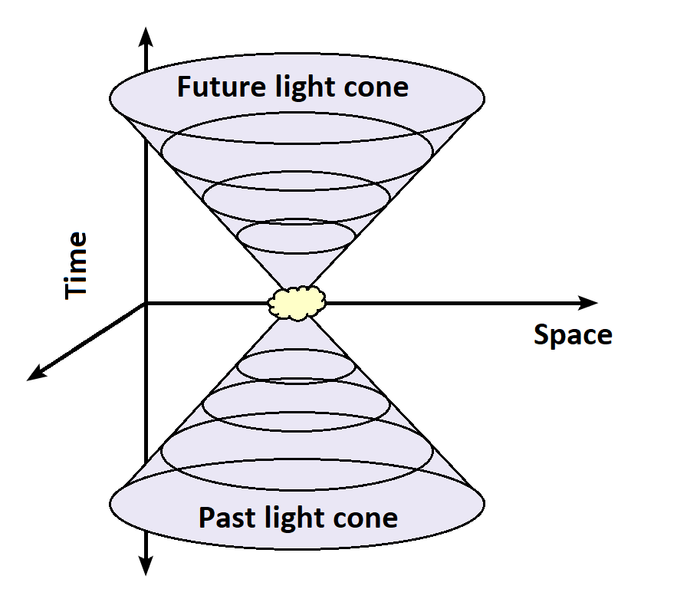
Согласно Специальной теории относительности, прошлое (причина) всегда предшествует будущему (следствию) / © Helen Klus
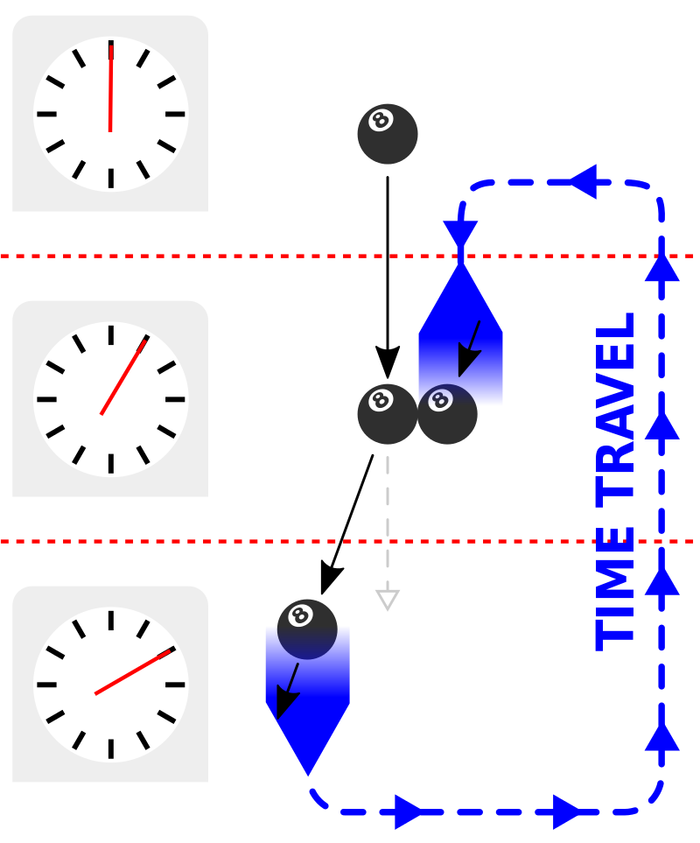
Давайте представим себе сценарий, в котором молодой талантливый изобретатель — назовем его Евгением — создает в 2018 году машину времени. Так как Евгений никогда не знал своего дедушку, он решает отправиться в прошлое, чтобы встретиться с ним. После тщательного исследования он выясняет, где именно находился его дедушка — все еще молодой и холостой — в 15:43, 22 ноября 1960 года. Он садится в машину времени и начинает свой путь.
К сожалению, Женя все воспринимает буквально, и, когда он выяснил, где будет его дедушка, он отправился именно в то самое место. Он «приземляется» прямо туда, где в этот момент должен находиться его дедушка… с весьма предсказуемым результатом. Проведя быстрый ДНК-тест, он понимает, что это действительно был отец его отца, садится обратно в машину и ждет своего исчезновения.
Игорь Дмитриевич Новиков / © Фотоархив ГАИШ МГУ
Эта идея позднее была расширена студентами Калтеха Фернандо Эшеверриа и Гуннаром Клинхаммером совместно с Кипом Торном. В своей статье они представили бильярдный шар, брошенный в прошлое через червоточину по траектории, которая в итоге помешала бы ему попасть в нее. Они утверждали, что физические свойства червоточины изменили бы траекторию шара таким образом, что он бы не смог помешать сам себе, или что шар не может попасть в червоточину по причине фактического вмешательства со стороны.
Таким образом, если следовать теории Новикова, любые действия, предпринятые путешественником во времени, становятся уже свершившейся историей, а наблюдателям эти события не дает увидеть горизонт Коши.
По возвращении в 2018 год наш Евгений обнаруживает, что дом его семьи пропал, как и другие следы его существования. Прочитав о теории Новикова и бильярдных шарах ученых из Калтеха, он проклинает Вселенную за бездействие. И в этот момент понимает, что, может, Вселенная не вмешалась, так как для этого требовалось некоторое корректирующее действие. Он бежит обратно к машине времени, чтобы изменить собственные действия и спасти свое будущее.
Решение Эшеверриа и Клинкхаммера / © Wikipedia
Решение Новикова может выглядеть несколько надуманным, так как для него определенно требуется множество механизмов, пока неизвестных физике. Именно по этой причине это решение «парадокса убитого дедушки» научное сообщество отвергает.
Может ли быть более экономное решение парадокса, построенное на уже существующих аспектах физики, введенных другими теориями? Оказывается, такая гипотеза, как многомировая интерпретация квантовой механики, может его предоставить. Многомировая интерпретация квантовой механики спешит на помощь!
Многомировую интерпретацию квантовой механики предложил Хью Эверетт III в 1950-х в качестве решения проблемы коллапса волновой функции, наблюдаемой в известном эксперименте Юнга с двумя щелями.
По мере прохождения через щель электрон может быть описан волновой функцией с конечной вероятностью прохождения либо через щель № 1, либо через щель № 2. Когда электрон появляется на экране, он выглядит размазанным, словно волна. А в других случаях проявляет себя как частица. Это называется коллапсом волновой функции. Другими словами, волна будто исчезает, а на ее месте остается частица. Это, в свою очередь, ключевой фактор Копенгагенской интерпретации квантовой механики. Но ученые не понимали, почему коллапсирует волновая функция.
Эверетт задал другой вопрос: а коллапсирует ли волновая функция вообще?
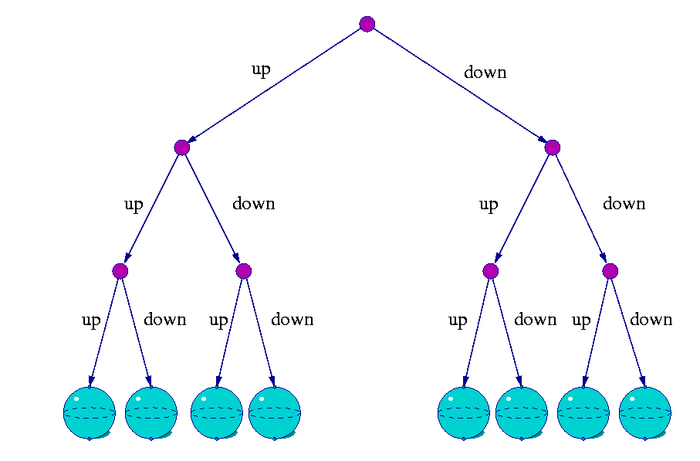
Он представил ситуацию, при которой волновая функция продолжает расти по экспоненте, не коллапсируя. В итоге вся Вселенная обретает одно из двух возможных состояний: «мир», в котором частица прошла через щель № 1, и «мир», в котором частица прошла через щель № 2. Эверетт утверждал, что такое же «деление» состояний происходит во всех квантовых событиях, многочисленные исходы которых существуют в разных мирах в состоянии суперпозиции. Волновая функция для нас выглядит так, будто она коллапсирует, поскольку мы живем в одном из таких миров, не способных взаимодействовать друг с другом.
Диаграмма разделения миров согласно многомировой интерпретации квантовой механики / © Wikipedia
Следовательно, когда Евгений прибывает в 1960 год, Вселенная разделяется. Он уже находится не в том мире, из которого прибыл (пусть это будет Мир № 1). Вместо этого он создал и занял новый мир. Когда он путешествует в будущее, то движется вместе с хронологией этого мира. Он никогда не существовал в нем и, по сути, никогда не убивал своего дедушку. Его дедушка продолжает существовать в добром здравии в Мире № 1.
Конечно, ни одно из предложенных решений и гипотез не делает путешествия во времени реальностью. Специальная теория относительности Эйнштейна и ограничения на скорость объекта с массой ставят серьезные преграды для этого. Тем не менее они предоставляют интересные решения головоломке. По иронии судьбы самое правдоподобное решение «парадокса убитого дедушки» исходит из единственной физической гипотезы, породившей еще больше фантастических историй, чем многие другие идеи и гипотезы, высказанные учеными за последнее столетие.
Любопытно, что многомировая интерпретация также может ответить на еще одну головоломку, связанную с путешествиями во времени. Если такая технология когда-то и станет чем-то большим, чем фантастика, где все путешественники во времени? Почему они до сих пор не прибыли к нам, чтобы рассказать о своем открытии?
Вероятный ответ — мы живем в первичном мире, в котором машинам времени суждено быть созданными. А изобретатели и их попутчики просто попадают в другие миры, которые сами и порождают. Если это действительно так, то изобретение машины времени приведет наш мир к тому, что из него пропадет множество физиков и изобретателей.
Аниме Закон Архимеда
Демон Максвелла | [Невозможные изобретения]
В древние времена самым простым, а иногда и единственным способом для достижения чего-либо невозможного человек считал обращение к помощи потусторонних сил.
Позже, вместе с бурным развитием наук появилась надежда, что технологический прогресс поможет устранить необходимость привлечения сверхъестественного для решения насущных проблем.
Но ведь потребности человека фактически не удовлетворимы, а границы желаемого расширяются намного быстрее, пределов достижимого.
Поэтому даже ученые иногда прибегают к помощи демонов, особенно когда им необходимо бросить вызов какому-нибудь фундаментальному научному закону. Например, второму началу термодинамики, неумолимая суровость которого, теоретически когда-нибудь приведет к концу своего существования всю нашу Вселенную.
Кстати, Томсон в 1851 году и сформулировал одно из определений второго закона термодинамики, который в его интерпретации звучит следующим образом: невозможен процесс, единственным результатом которого является получение системой теплоты от одного источника (теплового резервуара) и выполнение ею эквивалентного количества работы.
При этом Томсон опирался на исследования Сади Карно, который в 1824 году в своей работе «Размышления о движущей силе огня и о машинах, способных развивать эту силу», посвящённой паровым машинам, первым сформулировал идею, заложившую основу для понимания второго начала термодинамики:
при отсутствии разности температур теплота не может быть преобразована в работу; для постоянного производства работы тепловой машине необходимо иметь по крайней мере два тепловых резервуара с различными температурами — нагреватель и холодильник.
Но и здесь, если говорить о названиях, не все просто и однозначно. На самом деле, исторически первая формулировка закона и его определение «вторым началом термодинамики» принадлежат Рудольфу Клаузиусу.
Более того, понятие энтропии, её обозначение и название тоже были введены Клаузиусом в 1865 году.
Хотя, когда речь заходит об энтропии, большинство в первую очередь вспоминает Людвига Больцмана.
И раз речь, наконец, дошла до энтропии, то самое время вернуться к нашему демону.
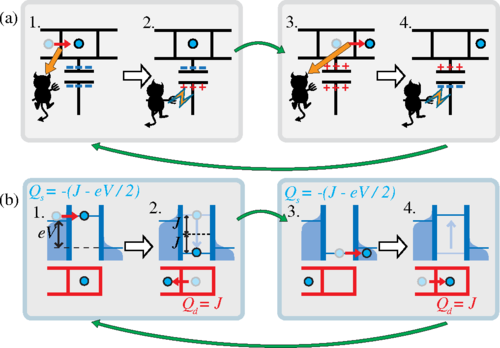
Итак, «демон» впервые появился в письме, которое Максвелл написал Питеру Гатри Тейту 11 декабря 1867 года в виде описания мысленного эксперимента, гипотетически позволяющего нарушать второй закон термодинамики. Позже он снова появился в письме Джону Уильяму Стратту в 1871 году, и только потом он был окончательно представлен публике в книге Максвелла 1872 года по термодинамике под названием «Теория тепла».
В своих письмах и книгах Максвелл описывал агента, открывающего дверь между комнатами, как «определенное существо» («finite being»). Как уже упоминалось, Уильям Томсон, он же лорд Кельвин, первым использовавший слово «демон» для концепции Максвелла в журнале Nature в 1874 году, на самом деле имел в виду посредническую, а не злобную коннотацию этого слова.
Согласно описанию Максвелла суть его мысленного эксперимента состоит в следующем:
Но это было бы слишком здорово, практически прямой путь к созданию вечного двигателя.
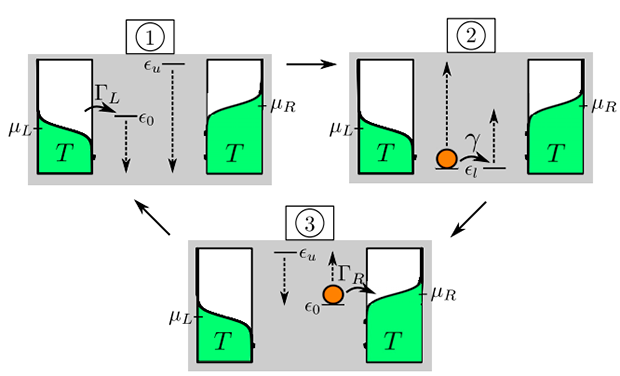
Все надежды на привлечение «демона Максвелла» к такому нужному делу были развеяны в 1929 году Лео Сцилардом. Сцилард обратил внимание на то, что реальный демон Максвелла должен иметь какие-то средства измерения молекулярной скорости и что получение информации тоже потребует затрат энергии. Поскольку демон и газ взаимодействуют, следует учитывать общую энтропию газа и демона вместе взятых. Расход энергии демоном вызовет увеличение энтропии демона, которое будет больше, чем понижение энтропии газа.
Звучит исчерпывающе! Казалось бы, вопрос закрыт? Снова «невозможное изобретение»!
Поскольку нарушение законов физики, в отличие от прочих законов, не грозит перспективой наказания, а вот на премию типа Нобелевской нарушитель вполне может рассчитывать, то желающих представить миру свою версию демона Максвелла превеликое множество.
Только за последнее десятилетие было предпринято несколько эффектных попыток.
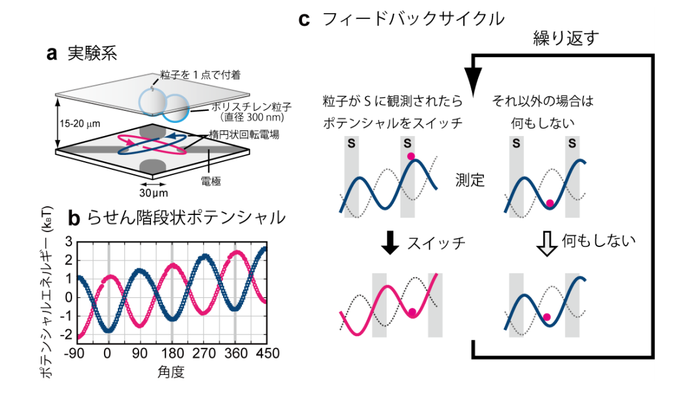
В 2010 году мысленный эксперимент в реальности удалось воплотить физикам из университетов Тюо и Токийского университета.
Японцы создали два связанных шарика полистирола диаметром 0,3 микрометра каждый. Один был прикреплен на поверхности стекла, а второй шарик-ротор мог вращаться вокруг первого.
Установку при этом заполняла жидкость. Её молекулы хаотично подталкивали шарики, создавая эффект броуновского движения. Поэтому, ротор мог вращаться с равной вероятностью, как по направлению часовой стрелки, так и против.
Авторы добавили слабое электрическое поле, которое создавало крутящий момент. Это был аналог лестницы, по которой шарик мог «взбираться», увеличивая потенциальную энергию. Иногда молекулы толкали ротор против действия поля (на подъём), а иногда в сторону поля (прыжок по ступенькам вниз). Но в целом ротор вращался туда, куда его толкало внешнее поле.
Но вот физики добавили «демона» — высокоскоростную камеру, наблюдающую за шариком, и компьютер, управляющий полем. Каждый раз, когда ротор в броуновском движении делал шаг против поля, компьютер сдвигал последнее так, что шарик мог повернуться, но когда ротор пытался вращаться обратно, поле блокировало его.
Так был создан аналог открываемой и закрываемой демоном Максвелла дверцы: ротор увеличивал свою энергию за счёт теплового движения молекул.
Законов природы, впрочем, установка не нарушает, поскольку для работы «демона» (то есть камеры, системы коррекции напряжения) необходима энергия. Но японцы подчёркивают, что данный опыт впервые на практике доказал реальность так называемого теплового насоса – варианта «демона Максвелла», теоретически обоснованного Лео Сцилардом в 1929 году. Такая машина извлекает энергию из изотермической окружающей среды и преобразует её в работу.
В 2016 году Физики из Финляндии, России и США создали электронную версию замкнутого (автономного) демона Максвелла. «Система» представляет собой одноэлектронный ящик, подключенный к внешнему потенциалу. Демон следит за зарядом на коробке. (Слева) Если электрон (синий) входит в ящик, демон немедленно захватывает его, прикладывая положительный заряд. (Справа) Если электрон покидает ящик, демон отталкивает его, прикладывая отрицательный заряд. Это электронный эквивалент того, как демон открывает или закрывает дверь для быстрых и медленных частиц в оригинальном мысленном эксперименте Максвелла.
В 2018 году физики в США упорядочили систему из 50 помещенных в трехмерную оптическую ловушку атомов цезия с помощью реального аналога демона Максвелла, уменьшив при этом энтропию системы почти в 2,5 раза.
В оптической ловушке атомы захватываются с помощью двух поляризованных лазеров, которые создают периодический удерживающий потенциал.
6 апреля 2020 года в журнале Physical Review B была опубликовано исследование, описывающее созданную учеными систему из двух квантовых точек с одноэлектронными переходами для оценки термодинамических характеристик демона Максвелла с учетом информации и возвратного действия измерений.
Они продемонстрировали возможность преобразования тепла в работу за счет информации и получили кривые зависимостей тепла и мощности от запирающего напряжения и степени туннелирования.
Это только самые удачные и поэтому самые нашумевшие эксперименты последних лет по созданию демона Максвелла.
Не стоит сомневаться, что попытки обмануть природу при содействии ловкого демона будут продолжаться и дальше до тех пор, пока они либо увенчаются успехом, либо вся Вселенная достигнет термодинамического равновесия…