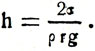высота поднятия жидкости в капилляре будет тем выше чем

25. Капиллярное поднятие жидкости, уравнение Жюрена

Процесс капиллярного поднятия жидкости является очень важным процессом и имеет достаточно широкое применение.

В этом случае можно рассматривать капиллярное давление (разность давлений в соседних фазах, которые разделены искривленной поверхностью) как добавление, которое в зависимости от знака кривизны может уменьшать или увеличивать давление внутри капли.

При контактах жидкостей с твердыми телами важной характеристикой является краевой угол смачивания, который может образовываться между поверхностями жидкости и твердого тела.

Если происходит достаточное смачивание твердой поверхности, при котором угол смачивания меньше 90°, говорят о гидрофильности вещества, если же угол велик и составляет больше 90°, говорят о процессах гидрофобности.

При условии смачивания поверхности жидкостью стенок капилляра ее поверхность будет казаться искривленной и иметь т. н. отрицательный радиус кривизны r.

В результате такого процесса давление в жидкости над поверхностью оказывается понижено по сравнению с тем давлением, при помощи которого жидкость будет подниматься по капилляру до тех пор, пока капиллярное давление не будет уравновешено:

где r 1 , r 11 – плотности жидкости и ее насыщенного пара; g – ускорение свободного падения; H – высота подъема жидкости.

Из уравнения Жюрена следует, что чем лучше жидкость смачивает стенки капилляра, тем выше происходит поднятие жидкости в капилляре при данном значении напряжения.

Если происходит несмачивание поверхности, жидкость способна образовывать некий выпуклый капиллярный мениск, этому условию будет отвечать повышение давления в жидкости под поверхностью самого мениска, и вместо поднятия жидкости происходит опускание жидкости.

Смачивание идет с уменьшением поверхностной энергии, при котором выделяется теплота. При лучшем смачивании твердого тела жидкостью теплота смачивания повышается. Метод капиллярного поднятия жидкости основан на рассмотренной выше формуле Жюрена.

При этом используют достаточно тонкие капилляры, что необходимо для обеспечения сферической поверхности мениска, но использование капилляров, которые смачиваются хорошо, позволяет избежать всех неувязок, которые могут возникать при определении краевого угла.

Существуют также полустатические методы определения поверхностного натяжения на границе жидкости.

Такое условие возможно при нарушении равновесия системы. Но при исследовании каждой новой системы необходим новый подбор оптимальных скоростей приближения к состоянию равновесия.

Этот процесс необходим, чтобы измерения не были очень долгими, т. к. для установления равновесия в системе требуется время.

Во всех методах используют приближенные значения и сравнивают с полученными данными для другой жидкости, для которой значение поверхностного натяжения известно с высокой точностью.

Данный текст является ознакомительным фрагментом.

Источник

Физика. 10 класс

§ 8-2. Смачивание. Капиллярные явления

Поверхность жидкости может граничить не только с газом, но и с твёрдым телом. Какие явления можно наблюдать в этом случае?

Смачивание. На границе соприкосновения твёрдых тел, жидкостей и газов наблюдаются явления смачивания или несмачивания, которые являются результатом взаимодействия между молекулами жидкости, твёрдого тела и газа. Они приводят к искривлению поверхности жидкости около поверхности твёрдого тела на границе с газом. При контакте жидкости с твёрдым телом возможны случаи, когда жидкость смачивает (частично или полностью) или не смачивает (частично или полностью) его. Так, ртуть хорошо смачивает чистые поверхности металлов и не смачивает чистое стекло. Вода хорошо смачивает чистое стекло и не смачивает жирные поверхности.

Свободная поверхность жидкости на границе с твёрдым телом искривляется, образуя мениск. Если жидкость смачивает поверхность тела, образуется вогнутый мениск ( рис. 57.3, а ), если не смачивает — выпуклый мениск ( рис. 57.3, б ). На границе соприкосновения трёх сред — твёрдой, жидкой и газообразной — жидкость принимает такую форму, при которой сумма потенциальной энергии жидкости в гравитационном поле Земли и поверхностной энергии всех тел минимальна (твёрдые тела также обладают поверхностной энергией). Поверхностное натяжение на границе твёрдого тела и жидкости обозначают σ_тж, на границе твёрдого тела и газа — σ_тг, на границе жидкости и газа — σ_жг. Если σ_тг ≥ σ_тж + σ_жг, то жидкость полностью смачивает поверхность твёрдого тела, покрывая его тонкой плёнкой. Если σ_тж ≥ σ_тг + σ_жг, то жидкость полностью не смачивает поверхность твёрдого тела, стягиваясь в каплю, несколько сплюснутую действием силы тяжести и силы реакции опоры. В большинстве случаев имеет место частичное смачивание ( рис. 57.4, а ) или частичное несмачивание ( рис. 57.4, б ).

1. Почему капля воды или масла растекается по поверхности дерева, а капля ртути не растекается ( рис. 57.5 )?

2. Почему перед окраской поверхность предварительно грунтуют — покрывают олифой?

Явление смачивания используют в промышленности и в быту. Хорошее смачивание необходимо при окраске и мытье разных тканей, нанесении лакокрасочных покрытий и т. д. На явлении смачивания основано склеивание различных изделий. Покрытие металлических изделий масляной плёнкой для их защиты от коррозии основано на несмачивании водой жирных поверхностей. Непромокаемую одежду изготавливают из тканей, которые не смачиваются водой ( рис. 57.6 ). Со свойством смачивания связана пайка металлов. Чтобы расплавленный припой хорошо растекался по поверхности металлических изделий и прилипал к ним, нужно эти поверхности очистить от жира, пыли и оксидной плёнки.

Источник

§ 7.7. Капиллярные явления

Под капиллярными явлениями понимают подъем или опускание жидкости в узких трубках — капиллярах(1) — по сравнению с уровнем жидкости в широких трубках.

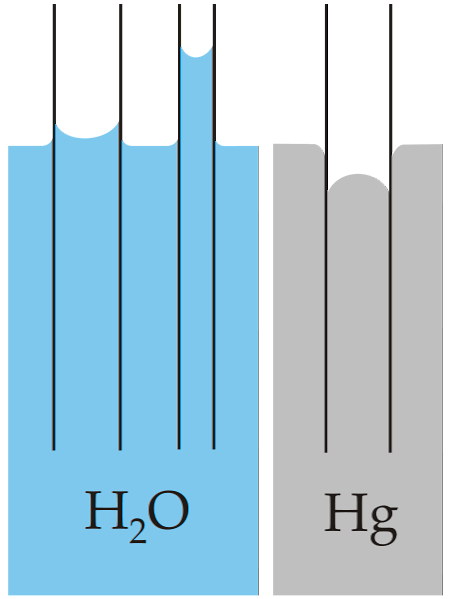
Смачивающая жидкость (например, вода в стеклянной трубке) поднимается по капилляру. При этом чем меньше радиус трубки, тем на большую высоту поднимается в ней жидкость (рис. 7.25). Жидкость, не смачивающая стенки капилляра (например, ртуть в стеклянной трубке), опускается ниже уровня жидкости в широком сосуде (рис. 7.26).

Почему смачивающая жидкость поднимается по капилляру, а несмачивающая опускается? В § 7.5 мы установили, что в случае полного смачивания и полного несмачивания мениск жидкости в узких трубках представляет собой полусферу, радиус которой равен радиусу канала трубки. Под вогнутым мениском смачивающей жидкости давление меньше, чем под плоской поверхностью (см. § 7.6). Поэтому жидкость в узкой трубке (капилляре) поднимается до тех пор, пока гидростатическое давление поднятой в капилляре жидкости на уровне плоской поверхности не скомпенсирует разность давлений. Под выпуклым мениском несмачивающей жидкости давление больше, чем под плоской поверхностью, и это ведет к опусканию несмачивающей жидкости в узких трубках.

Подъем смачивающей жидкости по капилляру можно объяснить по-другому — непосредственным действием сил поверхностного натяжения. Вдоль границы поверхностного слоя жидкости, имеющей форму окружности, на стенки трубки действует сила поверхностного натяжения, направленная вниз (для смачивающей жидкости). Такая же по модулю сила действует на жидкость со стороны стенок трубки вверх (третий закон Ньютона). Эта сила и заставляет жидкость подниматься в узкой трубке. Подъем смачивающей жидкости по капилляру прекратится тогда, когда сила, заставляющая жидкость подниматься вверх, уравновесится силой тяжести, действующей на поднятую жидкость.

Высота поднятия жидкости в капиллярных трубках

Пусть жидкость полностью смачивает стенки капилляра. Мениск ее в этом случае имеет форму полусферы (рис. 7.27) радиусом, равным радиусу канала капилляра r. Тогда непосредственно под вогнутым мениском (в точке А) давление жидкости будет меньше атмосферного давления р₀ на величину (см. § 7.6):

На глубине h, соответствующей уровню жидкости в широком сосуде (в точке В), к этому давлению прибавляется гидростатическое давление ρgh, где ρ — плотность жидкости. В широком сосуде на том же уровне, т. е. непосредственно под плоской поверхностью жидкости (в точке С), давление равно атмосферному давлению р₀. Так как жидкость находится в равновесии, то давления на одном и том же уровне (в точках В и С) равны. Следовательно,

Высота поднятия жидкости в капилляре прямо пропорциональна поверхностному натяжению ее и обратно пропорциональна радиусу канала капилляра и плотности жидкости.

Глубина h, на которую опускается в капилляре несмачивающая жидкость, тоже вычисляется по формуле (7.7.3). Это утверждение вы можете проверить самостоятельно.

Формулой (7.7.3) можно воспользоваться для определения поверхностного натяжения σ. Для этого необходимо по возможности точнее измерить высоту поднятия жидкости h и радиус канала трубки г. Зная плотность жидкости ρ, поверхностное натяжение σ можно найти по формуле

Это один из наиболее распространенных способов определения поверхностного натяжения.

Капиллярные явления в природе, быту и технике

Чрезвычайно важно для растений движение и сохранение воды в почве. Почва имеет рыхлое строение, и между отдельными частицами ее находятся промежутки. Узкие промежутки представляют собой капилляры. По капиллярным ходам вода поднимается к корневой системе растений и снабжает их необходимой влагой и питательными солями.

По капиллярам находящаяся в почве вода поднимается вверх и интенсивно испаряется (рис. 7.28). Чтобы уменьшить испарение, нужно разрушить капилляры. Это достигается разрыхлением почвы.

Иногда требуется, наоборот, усилить приток влаги по капиллярам. Тогда почву укатывают, увеличивая этим количество капиллярных каналов.

Любопытно, а может ли вода с растворенными в ней веществами подниматься к верхушкам высоких деревьев за счет поверхностного натяжения (высота, например, секвойи более 100 м). Радиус капилляров в древесине от 0,01 до 0,3 мм. Значит, в самых тонких капиллярах вода не поднимается выше 1,5 м. За счет атмосферного давления она может подняться не выше 10 м, даже если на конце трубки создать вакуум. Не может высоко поднять воду и осмотическое давление, благодаря которому давление в растворе больше, чем в чистой жидкости.

В быту капиллярные явления используют при самых разнообразных обстоятельствах. Прикладывая промокательную бумагу, удаляют излишек чернил с письма, хлопчатобумажной или льняной тряпкой вытирают мокрые места на столе или на полу. Применение полотенец, салфеток возможно только благодаря наличию в них капилляров. Поднятие керосина или расплавленного стеарина по фитилям ламп и свечей обусловлено наличием в фитилях капиллярных каналов. В технике как один из способов подвода смазки к деталям машин применяют иногда фитильный способ подачи масла.

В строительном деле приходится учитывать подъем влаги из почвы по порам строительных материалов. Из-за этого отсыревают стены зданий. Для защиты фундамента и стен от воздействия грунтовых вод и сырости применяют гидроизоляцию, покрывая фундамент горячим (жидким) битумом или обкладывая водонепроницаемым рулонным материалом (толь или рубероид).

Узких трубок (капилляров) в природе и технике великое множество. В этих трубках жидкость либо поднимается вверх на высоту h = , либо опускается вниз на расстояние, определяемое по той же формуле. Многие процессы в природе и технике вызываются этими движениями.

(1) От латинского слова capillaris — волосной.

Источник

Характеристики капиллярности и пример в воде

капиллярность Это свойство жидкостей, которое позволяет им перемещаться через трубчатые отверстия или пористые поверхности даже против силы тяжести. Для этого должны существовать баланс и координация двух сил, связанных с молекулами жидкости: когезия и адгезия; имея эти два физического отражения, называемого поверхностным натяжением.

Жидкость должна быть способной смачивать внутренние стенки трубки или поры материала, через который она движется. Это происходит, когда сила адгезии (жидкая стенка капиллярной трубки) больше, чем сила межмолекулярного сцепления. Следовательно, молекулы жидкости создают более сильные взаимодействия с атомами материала (стекло, бумага и т. Д.), Чем между ними..

Классический пример капиллярности иллюстрируется сравнением этого свойства для двух очень разных жидкостей: воды и ртути..

Верхнее изображение показывает, что вода поднимается через стенки трубки, что означает, что она имеет более высокие силы сцепления; в то время как с ртутью происходит обратное, потому что ее когезионные, металлические силы сцепления препятствуют смачиванию стекла.

Характеристики капиллярности

-Поверхность жидкости

Поверхность жидкости, например воды, в капилляре вогнутая; мениск вогнутый. Такая ситуация возникает из-за того, что результирующие силы, действующие на молекулы воды вблизи стенки трубки, направлены на это..

Во всем мениске есть угол контакта (θ), который представляет собой угол, который образует стенку капиллярной трубки с линией, касательной к поверхности жидкости в точке контакта.

Силы сцепления и сцепления

Если сила адгезии жидкости к стенке капилляра преобладает над силой межмолекулярного сцепления, то угол равен θ 90º; ртуть не смачивает стенку капилляра и поэтому опускается через ее внутреннюю стенку.

Когда капля ртути помещается на поверхность чистого стекла, капля сохраняет свою форму и угол θ = 140º.

-высота

Вода поднимается через капиллярную трубку, чтобы достичь высоты (h), при которой вес водяного столба компенсирует вертикальную составляющую силы межмолекулярного сцепления.

По мере подъема воды наступает момент, когда гравитация останавливает рост, даже если поверхностное натяжение работает в вашу пользу..

Когда это происходит, молекулы не могут продолжать «карабкаться» вверх по внутренним стенкам, и все физические силы уравниваются. С одной стороны, у вас есть силы, которые способствуют подъему воды, а с другой стороны, ваш собственный вес отталкивает ее вниз..

Закон Юрина

Это можно записать математически следующим образом:

2 π rΥcosθ = ρgπr 2 час

Где левая часть уравнения зависит от поверхностного натяжения, величина которого также связана с когезией или межмолекулярными силами; Cosθ представляет угол контакта, а r радиус отверстия, через которое поднимается жидкость.

И в правой части уравнения мы имеем высоту h, силу тяжести g и плотность жидкости; это будет вода.

Очистка тогда ч у вас есть

Эта формулировка известна как закон Юрина, который определяет высоту, достигаемую столбом жидкости в капиллярной трубке, когда вес столба жидкости уравновешивается силой подъема по капиллярности..

-Поверхностное натяжение

Вода является диполярной молекулой из-за электроотрицательности атома кислорода и его молекулярной геометрии. Это приводит к тому, что часть молекулы воды, в которой находится кислород, заряжена отрицательно, а часть молекулы воды, содержащая 2 атома водорода, заряжена положительно..

Молекулы внутри жидкости взаимодействуют благодаря множеству водородных связей, удерживая их вместе. Однако молекулы воды, находящиеся на границе раздела вода: воздух (поверхность), подвержены суммарному притяжению со стороны молекул жидкого синуса, не компенсируемому слабым притяжением с молекулами воздуха..

Следовательно, молекулы воды на границе раздела подвергаются воздействию силы притяжения, которая стремится удалить молекулы воды с поверхности раздела; то есть водородные мостики, сформированные с молекулами в основании, тянут те, которые находятся на поверхности. Таким образом, поверхностное натяжение стремится уменьшить поверхность раздела вода: воздух.

Отношения с ч

Если вы посмотрите на уравнение закона Юрина, то обнаружите, что h прямо пропорционально Υ; следовательно, чем больше поверхностное натяжение жидкости, тем больше высота, которая может подниматься через капилляр или пору материала.

Таким образом, можно ожидать, что для двух жидкостей, A и B, с разным поверхностным натяжением, жидкость с наибольшим поверхностным натяжением поднимается до более высокой высоты..

Из этого можно сделать вывод, что высокое поверхностное натяжение является наиболее важной характеристикой, которая определяет капиллярное свойство жидкости..

-Радиус капилляра или поры, где поднимается жидкость

Соблюдение закона Юрина указывает на то, что высота, достигаемая жидкостью в капилляре или поре, обратно пропорциональна радиусу того же самого.

Следовательно, чем меньше радиус, тем больше высота, которую столб жидкости достигнет за счет капиллярного воздействия. Это можно увидеть непосредственно на изображении, где вода сравнивается с ртутью.

В стеклянной трубке с радиусом 0,05 мм толща воды по капиллярности достигнет высоты 30 см. В капиллярных трубках с радиусом 1 мкм при давлении всасывания 1,5 х 10 3 ГПа (что равно 1,5 атм) соответствует расчету высоты водяного столба от 14 до 15 м..

Это очень похоже на то, что происходит с теми соломинками, которые вращаются сами по себе несколько раз. При всасывании жидкости создается перепад давления, который вызывает подъем жидкости в рот.

Максимальное значение высоты столбца, достигаемое капиллярностью, является теоретическим, поскольку радиус капилляров не может быть уменьшен за пределы определенного предела..

Закон Пуазейля

Это устанавливает, что поток реальной жидкости задается следующим выражением:

При уменьшении радиуса капилляра высота столба жидкости, достигаемого капиллярностью, должна увеличиваться бесконечно. Однако Пуазейль указывает, что уменьшение радиуса также уменьшает поток жидкости через этот капилляр.

Кроме того, вязкость, которая является мерой сопротивления, которое противодействует потоку реальной жидкости, будет дополнительно уменьшать поток жидкости.

-Угол контакта (θ)

Чем выше значение cosθ, тем выше высота столба воды по капиллярности, как указано в законе Юрина.

Если θ мало и приближается к нулю (0), cosθ равно = 1, поэтому значение h будет максимальным. Наоборот, если θ равен 90º, cosθ = 0 и значение h = 0.

Когда значение θ больше 90º, как в случае выпуклого мениска, жидкость не поднимается капиллярно и имеет тенденцию к снижению (как это происходит с ртутью).

Капиллярность воды

Вода имеет значение поверхностного натяжения 72,75 Н / м, относительно высокое по сравнению со значениями поверхностного натяжения следующих жидкостей:

-Этиловый спирт: 22,75 н / м

Следовательно, вода обладает исключительным поверхностным натяжением, что способствует развитию капиллярного явления, столь необходимого для поглощения воды и питательных веществ растениями..

На растениях

Капиллярность является важным механизмом для поднятия сока ксилемой растений, но сама по себе она недостаточна для того, чтобы сок достиг листьев деревьев..

Транспирация или испарение является важным механизмом восхождения сока ксилемой растений. Листья теряют воду в результате испарения, вызывая уменьшение количества молекул воды, что вызывает притяжение молекул воды, присутствующих в капиллярных трубках (ксилема).

Молекулы воды не действуют независимо друг от друга, но взаимодействуют под действием сил Ван-дер-Ваальса, которые заставляют их подниматься, связанные капиллярными трубками растений, к листьям..

В дополнение к этим механизмам следует отметить, что растения поглощают воду из почвы посредством осмоса и что положительное давление, создаваемое в корне, приводит к началу подъема воды через капилляры растения..

Источник

Высота поднятия жидкости в капилляре будет тем выше чем

§ 19. Капиллярные явления

Продолжим изучение явлений, которые объясняются поверхностным натяжением и смачиванием жидкости.

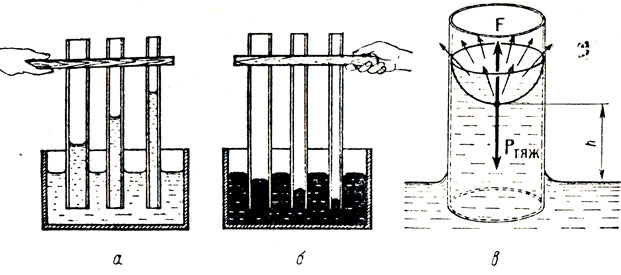
Рис. 20. Жидкости в капиллярах

Мы знаем, что под действием сил поверхностного натяжения поверхность жидкости стремится сократиться. Вследствие этого поверхность вогнутого мениска стремится выпрямиться и сделаться плоской (рис. 20, в). При этом она тянет за собой частицы жидкости, лежащие под ней, и жидкость поднимается по капилляру вверх. Но поверхность жидкости в узкой трубке плоской оставаться не может, она должна иметь форму вогнутого мениска. Как только в новом положении данная поверхность примет форму мениска, она снова будет стремиться сократиться и т. д. В результате действия этих двух причин смачивающая жидкость и поднимается по капилляру. Поднятие прекратится, когда сила тяжести Р_тяж поднятого столба жидкости, которая тянет поверхность вниз, уравновесит равнодействующую силу F сил поверхностного натяжения, изображенных маленькими векторами и направленных касательно к каждой точке поверхности.

Сила тяжести, действующая на поднятую жидкость,

Подъем жидкости прекращается, когда Р_тяж = F или ρπr 2 hg = σ2πr. Отсюда высота поднятия жидкости в капилляре

Высота поднятия в капиллярах смачивающей жидкости и опускания несмачивающей обратно пропорциональна радиусу капилляра и плотности жидкости.

Источник