выберите то что является множество решений неравенства ctg x a

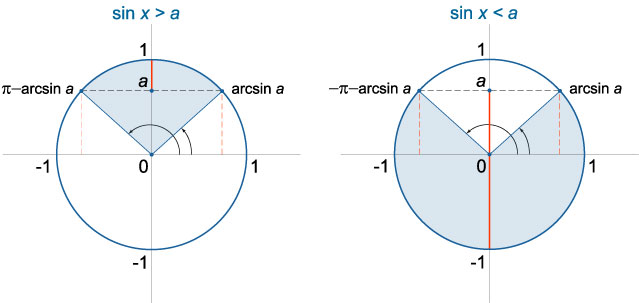
Неравенство \(sinx≤a\)

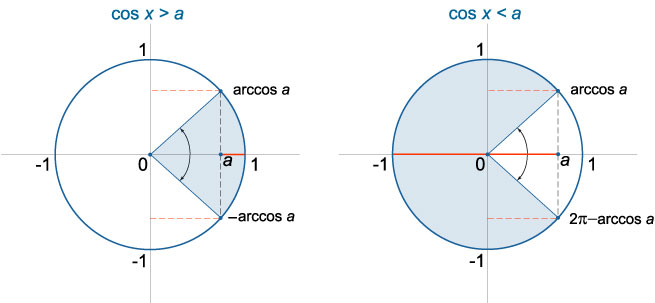
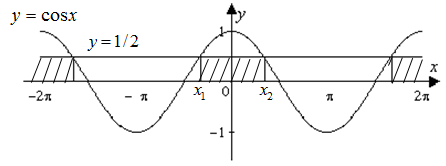
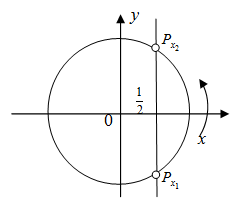
Неравенство \(cosx>a\)

Неравенство \(cosx≥a\)

Неравенство \(cosx

Неравенство \(cosx≤a\)

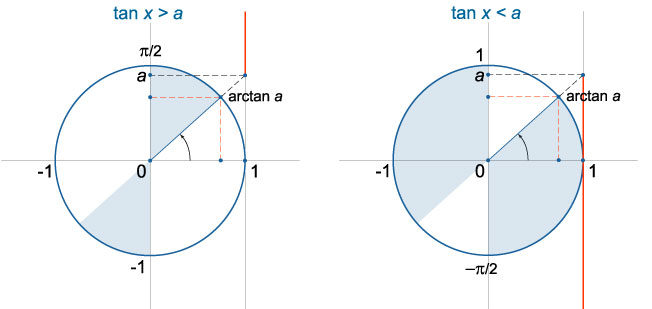
Неравенство \(tgx>a\)

Неравенство \(tgx≥a\)

Неравенство \(tgx

Неравенство \(tgx≤a\)

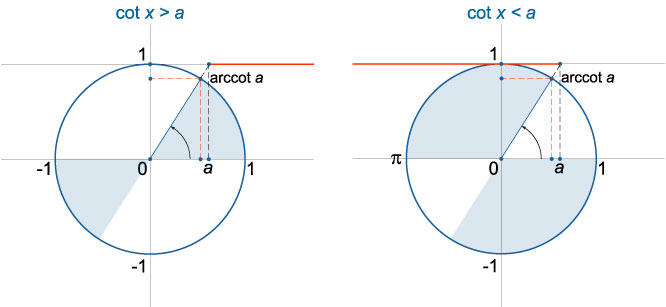
Неравенство \(ctgx>a\)

Неравенство \(ctgx≥a \)

Неравенство \(ctgx

Неравенство \(ctgx≤a\)

Решение: Данное неравенство можно решить двумя способами: графически и с помощью единичного круга. Рассмотрим каждый из способов.

Источник

Тест с ответами: “Простейшие тригонометрические уравнения”

1. Решением какого из ниже перечисленных уравнений является такой ответ x = 2πk:
а) cos x = 1 +
б) sin x = 0
в) ctg x = 1

2. Простейшими тригонометрическими уравнениями называют уравнения вида:
а) cos a = x
б) cos x = a +
в) cos x = bx

3. Решите уравнение cos x = √ 3/2:
а) x = ±π/3 + 2πk
б) x = ± 2π/3 + 2πk
в) x = ±π/6 + 2πk +

4. Простейшими тригонометрическими уравнениями называют уравнения вида:
а) tg x = a +
б) tg a = x
в) tg x = bx

6. Простейшими тригонометрическими уравнениями называют уравнения вида:
а) ctg a = x
б) ctg x = a +
в) ctg x = bx

7. Решите уравнение tg x = √3/3:
а) x = π/3 + πk
б) x = ±π/3 + 2πk
в) x = π/6 + πk +

8. “a” в тригонометрическом уравнении:
а) произвольное число +
б) основополагающее число
в) знаковое число

9. Решите уравнение sin x = 0:
а) x = π + 2πk
б) x = 2πk
в) x = πk +

10. Решение тригонометрического уравнения состоит из … этапов:
а) трех
б) двух +
в) четырех

11. Найти корни уравнения сos(x)=1:
а) 0+ 2π +
б) 0
в) 1

12. Один из этапов решения тригонометрического уравнения:
а) преобразование уравнения для получения его сложного вида
б) преобразование уравнения для получения его простейшего вида +
в) решение полученного сложного тригонометрического уравнения

13. Тригонометрическое уравнение:
а) тригонометрическая функция с неизвестным в качестве аргумента +
б) сos(x)=1
в) уравнения, не требующие никаких преобразований

14. Один из этапов решения тригонометрического уравнения:
а) решение полученного сложного тригонометрического уравнения
б) преобразование уравнения для получения его сложного вида
в) решение полученного простейшего тригонометрического уравнения +

15. 90 градусов:
а) π/2 +
б) π/4
в) π/6

16. Существует … основных методов решения тригонометрических уравнений:
а) пять
б) семь +
в) шесть

17. Скольким градусам соответствует π в тригонометрии:
а) 90
б) 45
в) 180 +

18. Один из основных методов решения тригонометрических уравнений:
а)
б) алгебраический метод +
в)

19. Число π в общем случае-это:
а) отношение радиуса окружности к ее диаметру
б) отношение длины окружности к ее радиусу
в) отношение длины окружности к ее диаметру +

20. Один из основных методов решения тригонометрических уравнений:
а) разложение на частное
б) разложение на множители +
в) разложение на множимые

21. Укажите наименьший положительный корень уравнения 2sinx + 1 = 0:
а) 7π/6
б) π/6
в) 5π/6

22. Один из основных методов решения тригонометрических уравнений:
а) приведение к однозначимому уравнению
б) приведение к однородному уравнению +
в) приведение к квадратному уравнению

23. Решите уравнение cos2x-1=0:
а) 0
б) x=π-k
в) x=πk +

24. Один из основных методов решения тригонометрических уравнений:
а) переход к целому углу
б) переход к половинному углу +
в) переход к вспомогательному углу

25. Является ли число 5π/6 решением уравнения 2cos2x+4sinx=3:
а) нет
б) отчасти
в) да +

26. Один из основных методов решения тригонометрических уравнений:
а) введение отрицательного угла
б) введение вспомогательного угла +
в) введение прямого угла

27. При каких значениях а уравнение sinx=a имеет хотя бы одно решение:
а) [-1;1] +
б) 2
в) R

28. Один из основных методов решения тригонометрических уравнений:
а) преобразование разности в сумму
б) преобразование произведения в разность
в) преобразование произведения в сумму +

29. Простейшими тригонометрическими уравнениями называют уравнения вида:
а) sin x = a +
б) sin a = x
в) sin x = bx

30. Один из основных методов решения тригонометрических уравнений:
а) общепринятая подстановка
б) универсальная подстановка +
в) закрепленная подстановка

Источник

Тригонометрические неравенства и методы их решения

Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.

Методы решений неравенств:

При решении более сложных тригонометрических неравенств пользуются двумя основными приемами:

I. Данное неравенство с помощью равносильных преобразований сводится к простейшим тригонометрическим неравенствам. При выполнении преобразований пользуются теми же приемами, что и при решении тригонометрических уравнений.

II. Применяется метод интервалов для определения числовых промежутков, в которых содержатся решения неравенства. Предварительно решается соответствующее тригонометрическое уравнение и устанавливаются интервалы знакопостоянства с учетом области определения неравенства.

Неравенство \(sinx>a\)

Неравенство \(sinx≥a\)

Неравенство \(sinx

Неравенство \(sinx≤a\)

Неравенство \(cosx>a\)

Неравенство \(cosx≥a\)

Неравенство \(cosx

Неравенство \(cosx≤a\)

Неравенство \(tgx>a\)

Неравенство \(tgx≥a\)

Неравенство \(tgx

Неравенство \(tgx≤a\)

Неравенство \(ctgx>a\)

Неравенство \(ctgx≥a \)

Неравенство \(ctgx

Неравенство \(ctgx≤a\)

Решение: Данное неравенство можно решить двумя способами: графически и с помощью единичного круга. Рассмотрим каждый из способов.

Источник