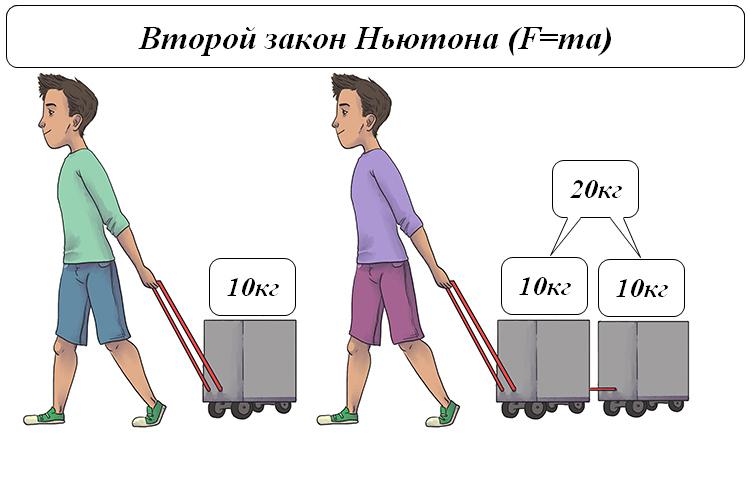
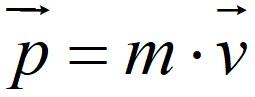второй закон ньютона утверждает что

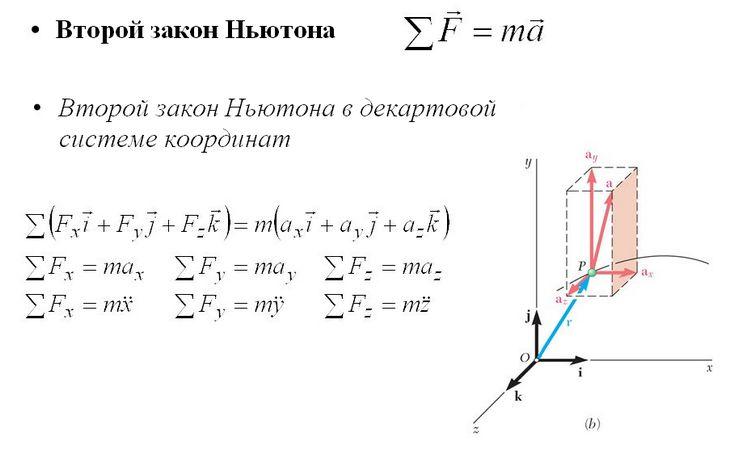
Второй закон Ньютона

Второй закон Ньютона — дифференциальный закон движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил. Один из трёх законов Ньютона.

Второй закон Ньютона в его наиболее распространённой формулировке утверждает: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела).

В приведённой формулировке второй закон Ньютона справедлив только для скоростей, много меньших скорости света и в инерциальных системах отсчёта.

Содержание

Формулировки

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Уравнения, соответствующие данному закону, называются уравнениями движения материальной точки.

Применимость различных формулировок

Второй закон Ньютона в виде приближённо справедлив только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. В виде второй закон Ньютона точно справедлив также в инерциальных системах отсчёта специальной теории относительности и в локально инерциальных системах отсчёта общей теории относительности.

Примечания

См. также

Полезное

Смотреть что такое «Второй закон Ньютона» в других словарях:

Ньютона второй закон — Второй закон Ньютона дифференциальный закон движения, описывающий взаимосвязь между равнодействующей всех приложенных к телу сил и ускорением этого тела. Один из трёх законов Ньютона. Второй закон Ньютона утверждает: в инерциальных системах… … Википедия

Ньютона законы — Классическая механика Второй закон Ньютона История… Фундаментальные понятия Пространство · Время · … Википедия

Закон сохранения энергии — Закон сохранения энергии фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и… … Википедия

Закон сохранения импульса — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия

Закон Мерсенна — Колебания струн пианино описываются дифференциальными уравнениями Спор о струне (также спор о колеблющейся струне, спор о звучащей струне) научная дискуссия, развернувшаяся в XVIII веке между математиками вокруг изучения колебаний струны.… … Википедия

Закон равнораспределения — Тепловое движение α пептида. Сложное дрожащее движение атомов, составляющих пептид, случайно, и энергия отдельного атома флуктуирует в широких пределах, но с помощью закона равнораспределения вычисляют как среднюю кинетическую энергию каждого… … Википедия

Закон (физика) — У этого термина существуют и другие значения, см. Закон (значения). Физический закон эмпирически установленная и выраженная в строгой словесной и/или математической формулировке устойчивая связь между повторяющимися явлениями, процессами и… … Википедия

Закон сохранения массы — Механика сплошных сред … Википедия

НЬЮТОНА ЧИСЛО — один из критериев подобия механич. движения, к рый получается из уравнения, выражающего второй закон Ньютона: где Р характерное давление, плотность и характерная скорость … Математическая энциклопедия

НЬЮТОНА ЗАКОНЫ МЕХАНИКИ — три закона, лежащие в основе т. н. классич. механики или механики Ньютона. Сформулированы И. Ньютоном (1687). Первый закон: «Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку… … Физическая энциклопедия

Источник

Вывод формулы второго закона Ньютона

В «Математических началах натуральной философии» Ньютона сформулирован закон, который в двадцатом веке охарактеризован Эйнштейном как главный постулат механики и считается фундаментом теоретической физики.

Второй закон Ньютона формулировка

Ньютон, формулируя постулат, связывал движущую силу и изменение количества движения.

Современная трактовка использует более привычные для восприятия термины, сегодня 2-й закон Ньютона звучит как:

В системах отсчёта, называемых инерциальными, материальная точка приобретает ускорение, сонаправленное силе или равнодействующей сил, являющихся возбудителями движения, и находящееся в прямо пропорциональной зависимости от неё. Также упомянутое ускорение обратно пропорционально массе движущейся материальной точки.

Трактовать постулат динамики можно через импульс – меру движения тела, численно равную результату умножения массы на скорость:

где p, m, v – импульс, масса, скорость тела или точки.

Вторая формулировка второго закона Ньютона гласит:

В системах отсчёта, называемых инерциальными, скорость изменения импульса, имеющего также название «количество движения», численно равно силе или равнодействующей сил, являющихся возбудителями движения материальной точки.

Область применения

2-й закон Ньютона применяют к материальным точкам – объектам массой, сосредоточенной в точке, и размерами, которыми допустимо пренебречь. Логичен вывод, что постулат механики работает в случаях, где масса тела остаётся постоянной. Также формулу свободно применяют в задачах движения центра масс системы, используя одноимённую теорему.

Формулировки отмечают ограниченность применимости закона инерциальными системами отсчёта. Однако, если внести силы инерции в равнодействующую, уравнение движения, составленное на основе постулата Ньютона, допустимо использовать в неинерциальных системах.

Вывод закона на основании проведённых опытов

Изучаемый фундамент динамики (динамика – наука, изучающая движение) не удастся вывести путём математических вычислений, формулу доказывают опытом, представленным рисунком.

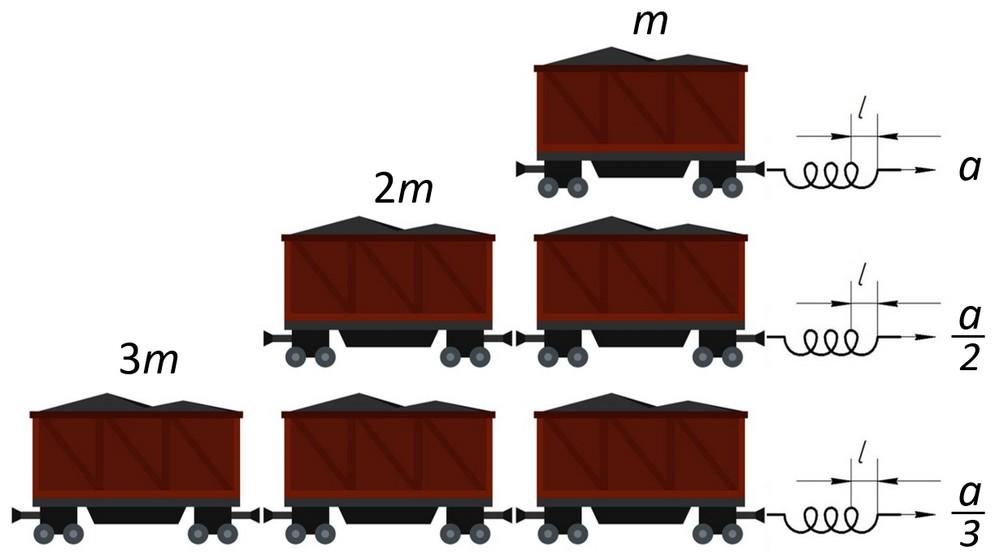
Тележка массой m взаимодействует с пружиной, растянутой на длину l. Если тянуть конец пружины, соблюдая выбранное значение деформации, тележка покатится по направлению воздействия, обладая ускорением a. Увеличим вес, добавив тележку, идентичную используемой, и снова потянем свободный конец пружины, следя за постоянностью удлинения. Зафиксируем уменьшение ускорения. Для полноты эксперимента, добавив третью тележку, повторим опыт и заметим, что значение ускорения меньше.

В эксперименте прикладываемая нагрузка оставалась неизменной, что контролировалось путём использования одной пружины, деформированной на величину l.

Рассмотрим произведение массы на ускорение тележки:

То есть, рассмотренное произведение одинаково и зависит от меры оказанного воздействия :

,

Вывод формулы второго закона Ньютона — видео.

Зависимость между массой и ускорением

Согласно проиллюстрированному опыту, ускорение объекта уменьшается настолько, насколько увеличивается масса. Результаты эксперимента для наглядности приведём в табличный вид:

Значение (единицы измерения условные)	Значение (единицы измерения условные)
1	1
2	1/2
3	1/3

Вывод: ускорение обратно пропорционально массе.

Зависимость между силой и ускорением

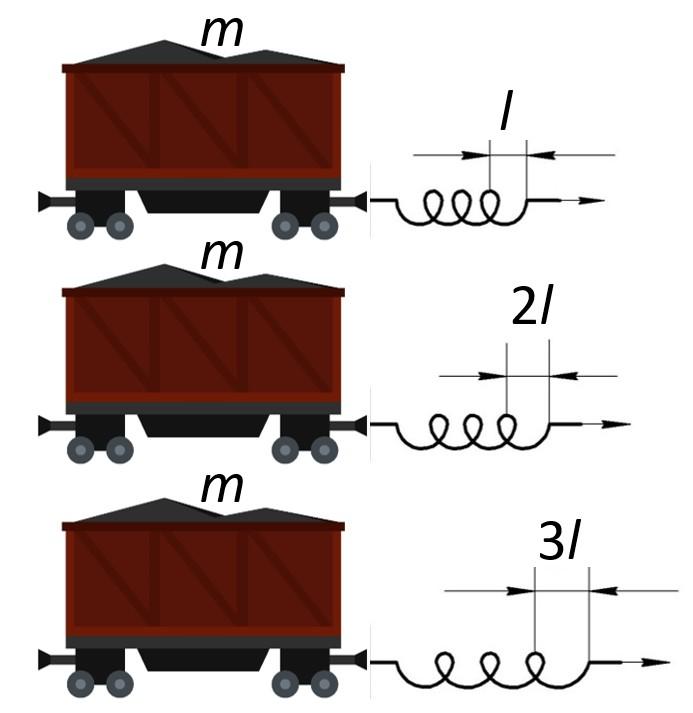
Для отражения связи между ускорением и силой придадим продемонстрированному опыту другую форму. К тележке массой m приложим силу, увеличивающуюся по модулю. Изменение нагрузки фиксируется за счёт возрастающей деформации пружины, тянущей тележку. В качестве эталонного проведём знакомый эксперимент: будем тянуть тележку массой m при помощи пружины с удлинением l и зафиксируем ускорение системы, равное a. Далее воздействуем на объект в два раза сильнее, растянув пружину до значения деформации 2l, и заметим, увеличение ускорения тележки до 2a. Для закрепления результата снова увеличим усилие, под действием которого растягивается пружина. По закону Гука, деформация пружины напрямую зависит от меры воздействия. Увеличив значение удлинения до 3l, увидим, что тележка двинется с ускорением 3a.

Анализируя эксперимент, делаем вывод: ускорение прямо пропорционально действующей силе.

Единица измерения силы

Международная система единиц, в привычном обозначении СИ – система интернациональная, называет ньютоны в качестве единиц, в которых измеряется сила. Ньютоны – производные единицы, выраженные основными (к ним относится семь наименований) путём умножения или деления последних друг на друга:

.

Справка: Фамилия Ньютон пишется с заглавной буквы, одноимённое название единиц измерений записывается со строчной.

Формула второго закона Ньютона

Формулу, выражающую закон Ньютона, записывают различными формами, в зависимости от системы координат. Стандартная запись:

в декартовой прямоугольной системе координат выглядит следующим образом:

,

где ,

– орты или единичные векторы.

В сферической и цилиндрической системах запись усложнена, однако все виды формулы выражают одну взаимосвязь силы, ускорения и массы.

Равнодействующая сила

Интуитивно значение силы, действующей на тело, ясно, однако второй закон Ньютона определении вносит незнакомый термин – «равнодействующая», и изначально сложно уверенно утверждать, о каком воздействии говорится.

Мало кто способен назваться гением по физике, однако каждому понятно, что любое тело испытывает воздействие нескольких сил одновременно. Сюда относятся, например, силы тяжести, сопротивления воздуха или упругости, реакция опоры. Для удобства расчётов прикладываемые к объекту воздействия сформировывают в одно – равнодействующую.

Совместное действие находят суммированием векторов внешних сил, приложенных к телу:

.

На практике подобное осуществляется проецированием векторов на координатные оси:

Если присутствует воздействие пары сил, действующих вдоль одной прямой, равнодействующая определяется как:

Таким образом, больше не возникнет вопроса, как читается выражение 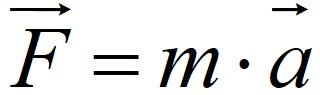, и изученный закон сразу будет формулироваться в мыслях.

Источник

Законы механики Ньютона

В отсутствие внешних силовых воздействий тело будет продолжать равномерно двигаться по прямой.

Ускорение движущегося тела пропорционально сумме приложенных к нему сил и обратно пропорционально его массе.

Всякому действию сопоставлено равное по силе и обратное по направлению противодействие.

Законы Ньютона — в зависимости от того, под каким углом на них посмотреть, — представляют собой либо конец начала, либо начало конца классической механики. В любом случае это поворотный момент в истории физической науки — блестящая компиляция всех накопленных к тому историческому моменту знаний о движении физических тел в рамках физической теории, которую теперь принято именовать классической механикой. Можно сказать, что с законов движения Ньютона пошел отсчет истории современной физики и вообще естественных наук.

Однако Исаак Ньютон взял названные в его честь законы не из воздуха. Они, фактически, стали кульминацией долгого исторического процесса формулирования принципов классической механики. Мыслители и математики — упомянем лишь Галилея (см. Уравнения равноускоренного движения) — веками пытались вывести формулы для описания законов движения материальных тел — и постоянно спотыкались о то, что лично я сам для себя называю непроговоренными условностями, а именно — обе основополагающие идеи о том, на каких принципах зиждется материальный мир, которые настолько устойчиво вошли в сознание людей, что кажутся неоспоримыми. Например, древним философам даже в голову не приходило, что небесные тела могут двигаться по орбитам, отличающимся от круговых; в лучшем случае возникала идея, что планеты и звезды обращаются вокруг Земли по концентрическим (то есть вложенным друг в друга) сферическим орбитам. Почему? Да потому, что еще со времен античных мыслителей Древней Греции никому не приходило в голову, что планеты могут отклоняться от совершенства, воплощением которой и является строгая геометрическая окружность. Нужно было обладать гением Иоганна Кеплера, чтобы честно взглянуть на эту проблему под другим углом, проанализировать данные реальных наблюдений и вывести из них, что в действительности планеты обращаются вокруг Солнца по эллиптическим траекториям (см. Законы Кеплера).

Первый закон Ньютона

Учитывая столь серьезный, исторически сложившийся провал, первый закон Ньютона сформулирован безоговорочно революционным образом. Он утверждает, что если какую-либо материальную частицу или тело попросту не трогать, оно будет продолжать прямолинейно двигаться с неизменной скоростью само по себе. Если тело равномерно двигалось по прямой, оно так и будет двигаться по прямой с неизменной скоростью. Если тело покоилось, оно так и будет покоиться, пока к нему не приложат внешних сил. Чтобы просто сдвинуть физическое тело с места, к нему нужно обязательно приложить стороннюю силу. Возьмем самолет: он ни за что не стронется с места, пока не будут запущены двигатели. Казалось бы, наблюдение самоочевидное, однако, стоит нам отвлечься от прямолинейного движения, как оно перестает казаться таковым. При инерционном движении тела по замкнутой циклической траектории его анализ с позиции первого закона Ньютона только и позволяет точно определить его характеристики.

Представьте себе что-то типа легкоатлетического молота — ядро на конце струны, раскручиваемое вами вокруг вашей головы. Ядро в этом случае движется не по прямой, а по окружности — значит, согласно первому закону Ньютона, его что-то удерживает; это «что-то» — и есть центростремительная сила, которую вы прилагаете к ядру, раскручивая его. Реально вы и сами можете ее ощутить — рукоять легкоатлетического молота ощутимо давит вам на ладони. Если же вы разожмете руку и выпустите молот, он — в отсутствие внешних сил — незамедлительно отправится в путь по прямой. Точнее будет сказать, что так молот поведет себя в идеальных условиях (например, в открытом космосе), поскольку под воздействием силы гравитационного притяжения Земли он будет лететь строго по прямой лишь в тот момент, когда вы его отпустили, а в дальнейшем траектория полета будет всё больше отклоняться в направлении земной поверхности. Если же вы попробуете действительно выпустить молот, выяснится, что отпущенный с круговой орбиты молот отправится в путь строго по прямой, являющейся касательной (перпендикулярной к радиусу окружности, по которой его раскручивали) с линейной скоростью, равной скорости его обращения по «орбите».

Теперь заменим ядро легкоатлетического молота планетой, молотобойца — Солнцем, а струну — силой гравитационного притяжения: вот вам и ньютоновская модель Солнечной системы.

Такой анализ происходящего при обращении одного тела вокруг другого по круговой орбите на первый взгляд кажется чем-то само собой разумеющимся, но не стоит забывать, что он вобрал в себя целый ряд умозаключений лучших представителей научной мысли предшествующего поколения (достаточно вспомнить Галилео Галилея). Проблема тут в том, что при движении по стационарной круговой орбите небесное (и любое иное) тело выглядит весьма безмятежно и представляется пребывающим в состоянии устойчивого динамического и кинематического равновесия. Однако, если разобраться, сохраняется только модуль (абсолютная величина) линейной скорости такого тела, в то время как ее направление постоянно меняется под воздействием силы гравитационного притяжения. Это и значит, что небесное тело движется равноускоренно. Кстати, сам Ньютон называл ускорение «изменением движения».

Первый закон Ньютона играет и еще одну важную роль с точки зрения нашего естествоиспытательского отношения к природе материального мира. Он подсказывает нам, что любое изменение в характере движения тела свидетельствует о присутствии внешних сил, воздействующих на него. Условно говоря, если мы наблюдаем, как железные опилки, например, подпрыгивают и налипают на магнит, или, доставая из сушилки стиральной машины белье, выясняем, что вещи слиплись и присохли одна к другой, мы можем чувствовать себя спокойно и уверенно: эти эффекты стали следствием действия природных сил (в приведенных примерах это силы магнитного и электростатического притяжения соответственно).

Второй закон Ньютона

Если первый закон Ньютона помогает нам определить, находится ли тело под воздействием внешних сил, то второй закон описывает, что происходит с физическим телом под их воздействием. Чем больше сумма приложенных к телу внешних сил, гласит этот закон, тем большее ускорение приобретает тело. Это раз. Одновременно, чем массивнее тело, к которому приложена равная сумма внешних сил, тем меньшее ускорение оно приобретает. Это два. Интуитивно эти два факта представляются самоочевидными, а в математическом виде они записываются так:

где F — сила, m — масса, а — ускорение. Это, наверное, самое полезное и самое широко используемое в прикладных целях из всех физических уравнений. Достаточно знать величину и направление всех сил, действующих в механической системе, и массу материальных тел, из которых она состоит, и можно с исчерпывающей точностью рассчитать ее поведение во времени.

Именно второй закон Ньютона придает всей классической механике ее особую прелесть — начинает казаться, будто весь физический мир устроен, как наиточнейший хронометр, и ничто в нем не ускользнет от взгляда пытливого наблюдателя. Назовите мне пространственные координаты и скорости всех материальных точек во Вселенной, словно говорит нам Ньютон, укажите мне направление и интенсивность всех действующих в ней сил, и я предскажу вам любое ее будущее состояние. И такой взгляд на природу вещей во Вселенной бытовал вплоть до появления квантовой механики.

Третий закон Ньютона

За этот закон, скорее всего, Ньютон и снискал себе почет и уважение со стороны не только естествоиспытателей, но и ученых-гуманитариев и попросту широких масс. Его любят цитировать (по делу и без дела), проводя самые широкие параллели с тем, что мы вынуждены наблюдать в нашей обыденной жизни, и притягивают чуть ли не за уши для обоснования самых спорных положений в ходе дискуссий по любым вопросам, начиная с межличностных и заканчивая международными отношениями и глобальной политикой. Ньютон, однако, вкладывал в свой названный впоследствии третьим закон совершенно конкретный физический смысл и едва ли замышлял его в ином качестве, нежели как точное средство описания природы силовых взаимодействий. Закон этот гласит, что если тело А воздействует с некоей силой на тело В, то тело В также воздействует на тело А с равной по величине и противоположной по направлению силой. Иными словами, стоя на полу, вы воздействуете на пол с силой, пропорциональной массе вашего тела. Согласно третьему закону Ньютона пол в это же время воздействует на вас с абсолютно такой же по величине силой, но направленной не вниз, а строго вверх. Этот закон экспериментально проверить нетрудно: вы постоянно чувствуете, как земля давит на ваши подошвы.

Тут важно понимать и помнить, что речь у Ньютона идет о двух силах совершенно разной природы, причем каждая сила воздействует на «свой» объект. Когда яблоко падает с дерева, это Земля воздействует на яблоко силой своего гравитационного притяжения (вследствие чего яблоко равноускоренно устремляется к поверхности Земли), но при этом и яблоко притягивает к себе Землю с равной силой. А то, что нам кажется, что это именно яблоко падает на Землю, а не наоборот, это уже следствие второго закона Ньютона. Масса яблока по сравнению с массой Земли низка до несопоставимости, поэтому именно его ускорение заметно для глаз наблюдателя. Масса же Земли, по сравнению с массой яблока, огромна, поэтому ее ускорение практически незаметно. (В случае падения яблока центр Земли смещается вверх на расстояние менее радиуса атомного ядра.)

По совокупности же три закона Ньютона дали физикам инструменты, необходимые для начала комплексного наблюдения всех явлений, происходящих в нашей Вселенной. И, невзирая на все колоссальные подвижки в науке, произошедшие со времен Ньютона, чтобы спроектировать новый автомобиль или отправить космический корабль на Юпитер, вы воспользуетесь все теми же тремя законами Ньютона.

Источник

Законы Ньютона

История…

Фундаментальные понятия
Пространство · Время · Масса · Сила Энергия · Импульс

Формулировки
Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби

Разделы
Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика

Учёные
Галилей · Кеплер · Ньютон Эйлер · Лаплас · Д’Аламбер Лагранж · Гамильтон · Коши

См. также: Портал:Физика

Зако́ны Ньюто́на — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год).

Содержание

Первый закон Ньютона

Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.

Современная формулировка

В современной физике первый закон Ньютона принято формулировать в следующем виде [1] :

Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.

Закон верен также в ситуации, когда внешние воздействия присутствуют, но взаимно компенсируются (это следует из 2-го закона Ньютона, так как скомпенсированные силы сообщают телу нулевое суммарное ускорение).

Историческая формулировка

Ньютон в своей книге «Математические начала натуральной философии» сформулировал первый закон механики в следующем виде:

Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (скажем, вращающейся) системе отсчёта закон инерции неверен. Поэтому ньютоновская формулировка нуждается в уточнениях.

Второй закон Ньютона

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).

Современная формулировка

В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

где — ускорение материальной точки;
— сила, приложенная к материальной точке;
— масса материальной точки.

Или в более известном виде:

В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил.

где — импульс точки,

где — скорость точки;

— время;
— производная импульса по времени.

Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:

Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности.

Нельзя рассматривать частный случай (при ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Историческая формулировка

Исходная формулировка Ньютона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Интересно, что если добавить требование инерциальной системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.

Третий закон Ньютона

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой , а второе — на первое с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Современная формулировка

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.

Историческая формулировка

Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.

Выводы

Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, если потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел , то возникает закон сохранения суммарной механической энергии взаимодействующих тел:

Законы Ньютона являются основными законами механики. Из них могут быть выведены уравнения движения механических систем. Однако не все законы механики можно вывести из законов Ньютона. Например, закон всемирного тяготения или закон Гука не являются следствиями трёх законов Ньютона.

Комментарии к законам Ньютона

Сила инерции

Законы Ньютона справедливы только в инерциальных системах отсчета. Если мы честно запишем уравнение движения тела в неинерциальной системе отсчета, то оно будет по виду отличаться от второго закона Ньютона: , где — это ускорение, наблюдаемое в рассматриваемой системе отсчёта, и — ускорение данной точки этой неинерциальной системы отсчёта относительно любой инерциальной системы отсчёта. Однако часто, для упрощения рассмотрения, вводят фиктивную «силу инерции» , и тогда эти уравнения движения переписываются в виде, идентичном второму закону Ньютона. Математически здесь всё корректно (правильно), но с точки зрения физики новую фиктивную силу нельзя рассматривать как нечто реальное, как результат некоторого реального воздействия на тело. Ещё раз подчеркнём: «сила инерции» — это лишь удобная параметризация того, как отличается движение в инерциальной и неинерциальной системах отсчета.

Законы Ньютона и Лагранжева механика

Законы Ньютона — не самый глубокий уровень формулирования классической механики. В рамках Лагранжевой механики имеется одна-единственная формула (запись механического действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), и из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами). Более того, в рамках Лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.

Решение уравнений движения

Уравнение является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию(перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.

Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.

Исторический очерк

Основные законы механики Ньютон сформулировал в своей книге «Математические начала натуральной философии» в следующем виде.

1. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
2. Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует.
3. Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.

LEX I
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.

LEX II
Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.

LEX III
Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.

Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей. Надо отметить, что Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов этот принцип является прямым следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».

Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта) и сила. Он ввёл в физику понятие массы как меры инерции и, одновременно, гравитационных свойств (ранее физики пользовались понятием вес).

Завершили математизацию механики Эйлер и Лагранж.

Источник