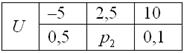
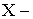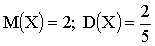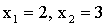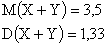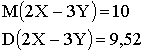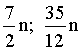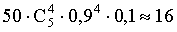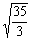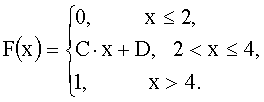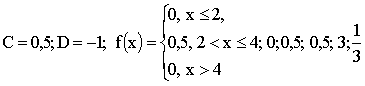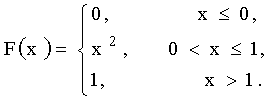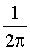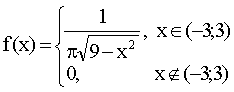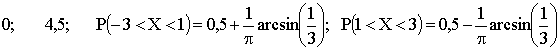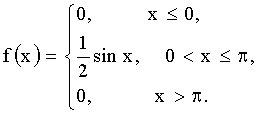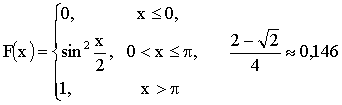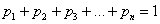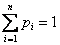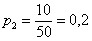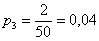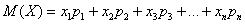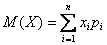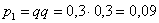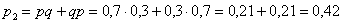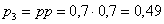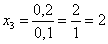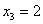вероятность того что случайная величина примет значения меньше заданного называется
Математика — онлайн помощь
Для теории вероятностей характерно то, что результаты рассматриваемых экспериментов можно представить числом, причем случайный характер исхода влечет и случайность этого числа.
Случайной величиной называется величина, которая в результате опыта может принять какое-либо числовое значение, заранее нам не известное.
Как видно из примеров по типу множества возможных значений случайные величины бывают дискретные, непрерывные и кусочно-непрерывные.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого промежутка.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
Существует универсальный способ задания закона распределения, который годится для случайных величин любого типа: функцией распределения случайной величины X называется функция F(X), равная вероятности того, что X примет значение меньше, чем число x,то есть 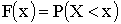
Из определения следует: 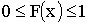
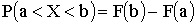
Непрерывную случайную величину можно также задать, используя другую функцию f(X)=F'(X), которую называют плотностью распределения вероятностей (иногда ее называют дифференциальной функцией).
Из определения следует:
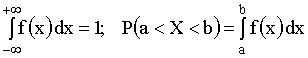
Одна из числовых характеристик, фиксирующая положение случайной величины на числовой оси, то есть некоторое среднее, ориентировочное значение случайной величины, около которого группируются ее возможные значения – математическое ожидание M(X).
Математическое ожидание вычисляется:
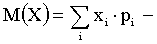
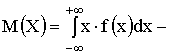
Дисперсия D(X) — есть характеристика рассеяния, разбросанности случайной величины около ее математического ожидания.
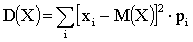
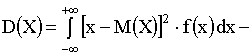
Иногда дисперсию удобно вычислять по следующей формуле:
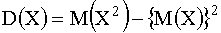
Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому вводится еще одна характеристика рассеяния – среднее квадратическое отклонение 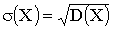
Математическое ожидание обладает следующими свойствами:
1. 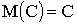
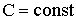
2. 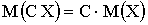
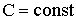
3. 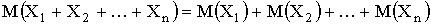
4. 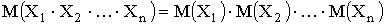
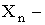
Дисперсия обладает следующими свойствами:
1.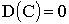
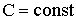
2.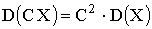
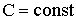
3.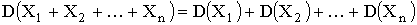
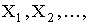
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.36. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 10 рублей. Написать закон распределения случайной величины X — стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение. Напишем возможные значения X: 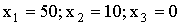
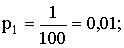
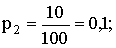
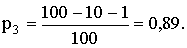
Напишем искомый закон распределения
ПРИМЕР 13.2.37. Функция распределения непрерывной случайной величины X задана выражением:
Найти: а) коэффициент a; б) найти плотность распределения f(X); в) найти вероятность того, что случайная величина X в результате опыта примет значение между 0,25 и 0,5.
Решение. а) Для непрерывной случайной величины функция F(x) непрерывна, следовательно, 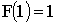
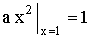
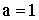
б) Плотность распределения 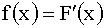
в) Воспользуемся формулой 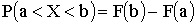
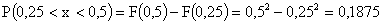
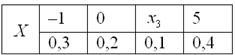
ПРИМЕР 13.2.38. Дискретная случайная величина X задана законом распределения
| X | 4 | 6 |  |
| P | 0,5 | 0,3 | 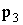 |
Найти: а) 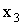
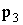
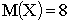
Решение. а) Известно, что 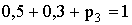
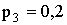
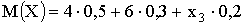
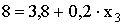
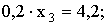
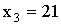
Закон распределения будет иметь вид:
б) Дисперсию можно вычислить двумя способами:
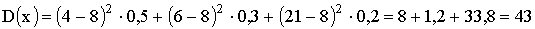
Для второго способа напишем закон распределения случайной величины 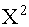
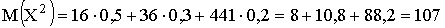
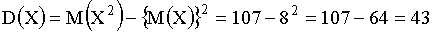
Примеры и задачи для самостоятельного решения
Решить задачи, используя формулы расчета вероятности для случайных величин
3.2.7.1. В урне 5 белых и 25 черных шаров. Вынули наугад 1 шар. Случайная величина X — число вынутых белых шаров.
а) построить ряд распределения СВ X;
б) построить функцию распределения СВ X;
б)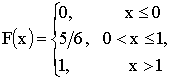
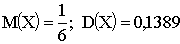
3.2.7.2. В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X — числа стандартных деталей среди отобранных. Найти M(X), D(X).
Отв.:
3.2.7.3. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа приборов таковы: 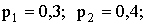
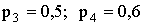
3.2.7.4. Случайная величина X — может принимать два возможных значения: 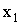
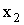
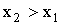
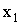
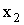
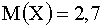
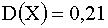
Отв.:
3.2.7.5. Дан перечень возможных значений дискретной случайной величины X : 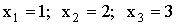
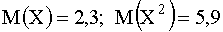
3.2.7.6. Даны независимые случайные величины X и Y.
Отв.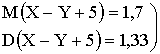
3.2.7.7. Брошены n игральных костей. Случайная величина X — сумма числа очков, которые выпадут на всех гранях. Найти: а) M(X); б) D(X).
Отв.:
3.2.7.8. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равно 0,9. Найти M(X) дискретной случайной величины X — числа партий, в каждой из которых окажется ровно четыре стандартных изделия, если проверке подлежит 50 партий.
Отв.:
3.2.7.9. Вероятность того, что в обувном магазине есть обувь, подходящей для покупателя модели, равна 0,6, а вероятность наличия обуви подходящего размера равна 0,8. Построить функцию распределения случайной величины X – числа обувных магазинов, которые посетит покупатель, если в городе три магазина.
| X | 1 | 2 | 3 |
| P | 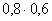 | 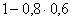 | 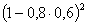 |
3.2.7.10. Имеется 6 ключей, из которых только один подходит к замку. Найти закон распределения случайной величины Х — числа попыток при открывании замка, если испробованный ключ в последующих попытках не участвует. Найти M(X) и 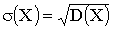
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| P | 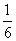 | 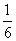 | 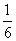 | 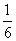 | 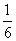 | 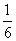 |
M(X)=3,5;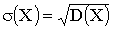
3.2.7.11. Два баскетболиста независимо друг от друга делают по одному броску в одну корзину. Вероятность попадания при одном броске равна 0,6 и 0,9 соответственно. Найти закон распределения случайной величины Х – числа попаданий в корзину. Найти M(X) и D(X).
| X | 0 | 1 | 2 |
| P | 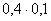 | 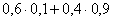 | 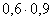 |
3.2.7.12. Вероятность того, что на АЗС есть в наличии бензин марки Аи-95, необходимый автомобилисту, равна 0,9. Построить функцию распределения случайной величины X – числа АЗС, которые посетит автомобилист, если в городе пять АЗС. Найти M(X), D(X).
3.2.7.13. Случайная величина X — задана функцией распределения
б) плотность распределения f(x) ;
в) 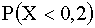
г) 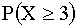
д) 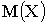
Отв.:
3.2.7.14. Случайная величина задана функцией распределения
Найти вероятность того, что в результате четырех независимых испытаний величина X — ровно три раза примет значение, принадлежащее интервалу (1/4; 3/4).
3.2.7.15. Плотность распределения непрерывной случайной величины X задана на всей оси Ox функцией
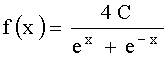
Найти постоянный параметр C.
Отв.:
3.2.7.16. Случайная величина X — задана плотностью распределения
Найти: а) математическое ожидание и дисперсию СВ X; б) установить, что вероятнее: в результате испытания окажется X 1.
Отв.:
3.2.7.17. Функция распределения случайной величины X — задана формулой 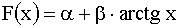
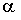
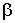
Отв.: 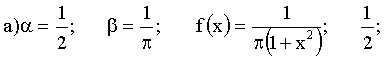
3.2.7.18. Случайная величина X имеет плотность распределения
Требуется а) Построить функцию распределения F(X).
б) Найти вероятность того, что в результате испытания 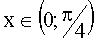
Отв.:
3.2.7.19. Среднее квадратическое отклонение каждой из 16 одинаково распределенных взаимно независимых случайных величин равно 10. Найти среднее квадратическое отклонение среднего арифметического этих величин.
Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Случайные величины. Дискретная случайная величина.
Математическое ожидание
Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:
Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.
Случайные величины, как правило, обозначают через 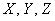
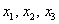
* Иногда используют 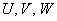
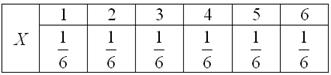
Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:
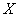
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина 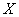
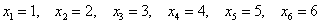
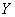
Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:
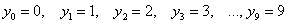
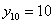
И, дабы соблюсти форму, немного физкультуры:
Её не в состоянии предугадать даже мастер спорта 🙂
Тем не менее, ваши гипотезы?
Коль скоро речь идёт о множестве действительных чисел, то случайная величина 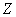
Таким образом, случайные величины целесообразно разделить на 2 большие группы:
1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.
…нарисовались непонятные термины? Срочно повторяем основы алгебры!
2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.
Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ
Сначала разберём дискретную случайную величину, затем – непрерывную.
Закон распределения дискретной случайной величины
– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей: 
Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».
А теперь очень важный момент: поскольку случайная величина 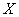
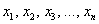
или, если записать свёрнуто:
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:
Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:
Некоторая игра имеет следующий закон распределения выигрыша:
Найти
…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.
Решение: так как случайная величина 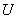
Разоблачаем «партизана»: 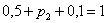
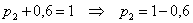
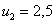
Контроль: 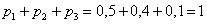
Ответ:
Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:
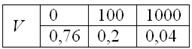
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины 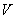
Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно 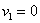
Всего таковых билетов 50 – 12 = 38, и по классическому определению:
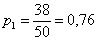
С остальными случаями всё просто. Вероятность выигрыша 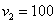
И для 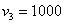
Проверка: 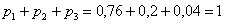
Ответ: искомый закон распределения выигрыша:
Следующее задание для самостоятельного решения:
Вероятность того, что стрелок поразит мишень, равна 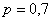
…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.
Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.
Математическое ожидание дискретной случайной величины
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина 
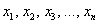
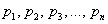
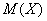
или в свёрнутом виде:
Вычислим, например, математическое ожидание случайной величины 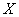
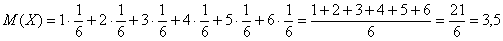
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.
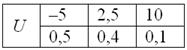
Теперь вспомним нашу гипотетическую игру:
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:
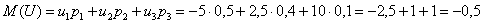
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины 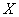
Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.
Но прежде будет полезно размять пальцы на клавишах калькулятора:
Случайная величина 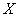
Найти 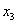
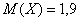
Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.
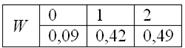
Пример 3. Решение: по условию 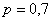
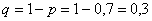
Составим 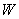
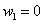
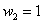
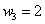
Проверка: 0,09 + 0,42 + 0,49 = 1
Ответ:
Примечание: можно было использовать обозначения 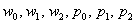
Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: 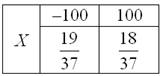
Вычислим математическое ожидание: 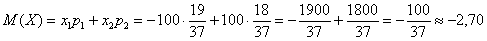
Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.
Пример 5. Решение: по определению математического ожидания: 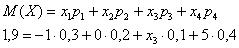
поменяем части местами и проведём упрощения: 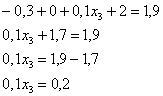
таким образом:
Выполним проверку: 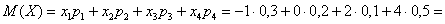
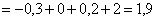
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5