верно ли что все равносторонние треугольники подобны

Три признака подобия треугольников

Теорема 1. Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

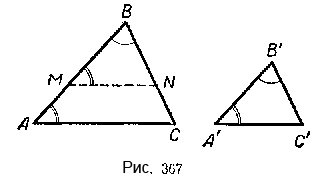
Пусть в треугольниках ABC и А’В’С ∠A = ∠А’ ∠В = ∠B’ (в подобных треугольниках вершины соответственно равных углов часто обозначают одинаковыми буквами).

Доказать, что \(\Delta\)ABС \(\sim\) \(\Delta\)А’В’С (рис. 367).

Прежде всего отметим, что из равенства двух углов данных треугольников следует, что и третьи углы их равны, т. е. ∠C = ∠С’.

Отложим от вершины В, например, на стороне AB треугольника ABC отрезок ВМ, равный отрезку А’В’. Из точки М проведём прямую MN || АС. Мы получили \(\Delta\)MBN, который подобен \(\Delta\)ABC. Но \(\Delta\)MBN = \(\Delta\)А’В’С’, так как ∠В = ∠В’ по условию теоремы; сторона MB = A’B’ по построению; ∠BMN = ∠A’ (∠BMN и ∠А’ порознь равны одному и тому же ∠А).

Если \(\Delta\)MBN \(\sim\) \(\Delta\)AВС, то \(\Delta\)А’В’С’ \(\sim\) \(\Delta\)ABC. Эта теорема выражает 1-й признак подобия треугольников.

Следствия. 1. Равносторонние треугольники подобны.

2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.

3. Два прямоугольных треугольника подобны, если она имеют по равному острому углу.

4. Равнобедренные прямоугольные треугольники подобны.

Пусть в треугольниках ABC и А’В’С’ \(\frac = \frac\) и ∠В = ∠В’

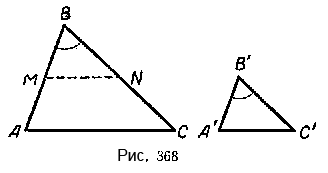
Требуется доказать, что \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’ (рис. 368).

Для доказательства отложим, например, на стороне AB треугольника ABC от вершины В отрезок ВМ, равный отрезку А’В’. Через точку М проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC.

Докажем, что \(\Delta\)MBN = \(\Delta\)А’В’С’. В этих треугольниках ∠В = ∠В’ по условию теоремы, MB = А’В’ по построению. Чтобы убедиться в равенстве сторон BN и В’С, составим пропорцию AB /_MB = BC /_BN (она вытекает из параллельности АС и MN) и сравним её с пропорцией, которая дана в условии теоремы: \(\frac = \frac\). В этих двух пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены,

т. е. В’С’ = BN. Отсюда следует равенство треугольников MBN и А’В’С’.

Так как \(\Delta\)MBN \(\sim\) \(\Delta\)А’В’С’, то, следовательно, и \(\Delta\)А’В’С’ \(\sim\) \(\Delta\)ABС.

Эта теорема выражает 2-й признак подобия треугольников.

Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.

Теорема 3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника.

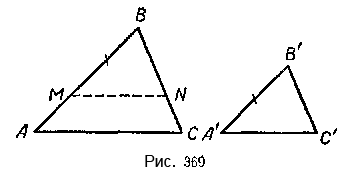
Пусть в треугольниках ABC и А’В’С’ \(\frac = \frac = \frac\) (рис. 369).

Требуется доказать, что \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’

Для доказательства отложим на стороне AB треугольника ABC от вершины В отрезок BM = А’В’. Из точки M проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC. Следовательно, \(\frac = \frac = \frac\).

Докажем, что \(\Delta\)MBN = \(\Delta\)А’В’С’. Для доказательства сравним две пропорции

\(\frac = \frac\) и \(\frac = \frac\).
В этих пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены, т.е. BN = В’С’.

Оказалось, что три стороны \(\Delta\)BMN равны трём сторонам \(\Delta\)А’В’С’, а именно:

MB = А’В’, BN = В’С’ и MN = А’С’.

Следовательно, \(\Delta\)MBN = \(\Delta\)А’В’С’, а \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’.

Эта теорема выражает 3-й признак подобия треугольников.

Источник

Подобие треугольников (ЕГЭ — 2022)

Что такое равные треугольники, понятно более или менее всем: их можно правильно наложить – и они совпадут.

А вот что такое подобные треугольники? Вроде как «похожие», но как это понимать? И для чего это понимать?

Ну например для решения задание ЕГЭ №16, где подобие треугольников используется для доказательств. Кстати, полностью 16-ю задачу решают менее 1% выпускников!

Читай эту статью, смотри вебинар по 16 задаче и все поймешь!

Подобие треугольников — коротко о главном

Подобные треугольники – это треугольники, у которых все углы равны и все стороны строго пропорциональны.

Коэффициент пропорциональности называется коэффициентом подобия \( \displaystyle k\).

\( \angle A = \angle ,\angle B = \angle ,\angle C = \angle \)

Отношение периметров подобных треугольников равно коэффициенту подобия: \( \displaystyle \frac<<

_>><<

_<<_<1>><_<1>><_<1>>>>>=k\).

Отношение площадей подобных треугольников равно квадрату коэффициента подобия: \( \displaystyle \frac<<_>><<_<<_<1>><_<1>><_<1>>>>>=<^<2>>\).

Признаки подобия треугольников:

По двум углам:

По одному углу и отношению заключающих его сторон:

По отношению трех сторон:

Подобные треугольники — подробнее

Мы разобрали подробно все, что касается треугольников в общем. Кроме того мы рассмотрели отдельные темы:

Но что такое подобные треугольники?

Вот, например, такой и такой:

Похожи эти треугольники? Ты скажешь, конечно же нет!

А вот такой и такой?

Посмотри внимательно, тоже похожи.

А теперь строго математически!

Треугольники называются подобными, если у них все углы равны и все стороны пропорциональны.

То есть все углы равны и все стороны одного треугольника в \( \displaystyle 5\), или, в \( \displaystyle 7\), или в \( \displaystyle 8,21\) (или и т.д.) больше сторон другого треугольника.

Записываются слова «треугольник \( \displaystyle ABC\) подобен треугольнику \( \displaystyle <_<1>><_<1>><_<1>>\)» с помощью такого значка:

То число раз, в которое отличаются стороны подобных треугольников, называются коэффициентом подобия, обозначается обычно с помощью буквы \( \displaystyle k\).

\(\angle A = \angle ,\angle B = \angle ,\angle C = \angle \)

Можно было бы все так и оставить, но, как и в случае с равенством треугольников, ленивым математикам стало слишком неохота проверять равенство ВСЕХ трех углов, и пропорциональность ВСЕХ трех сторон.

Признак подобия треугольников «по двум углам»

Помнишь еще, что «\( \displaystyle \sim<\ >\)» обозначает слова «подобен»?

Осознай удобство! Вместо того, чтобы проверять 6 утверждений – 3 равных угла и 3 пропорциональных стороны – ДОСТАТОЧНО РАВЕНСТВА ВСЕГО ДВУХ УГЛОВ! И это вообще-то самых удобный и часто используемый признак.

Но есть и еще два. Смотри.

Признак подобия треугольников «две пропорциональные стороны и угол между ними»

Признак подобия треугольников «три пропорциональные стороны»

Самый главный «секрет» подобия треугольников

Признаки нам рассказали о том, как обнаружить подобные треугольники, а теперь, как же воспользоваться найденным?

Ну вот, что же хорошего? А то, что тогда…

Все элементы одного треугольника ровно в \( \displaystyle 2\) (или сколько у тебя выйдет раз) больше, чем элементы другого треугольника.

Не только стороны, но и высоты, биссектрисы, медианы, радиусы вписанной и описанной окружности и т.д.

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 16. Подобие треугольников. Задачи на доказательство

Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!

Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.

Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.

В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.

Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.

Вы научитесь также применять подобие треугольников для расчетных задач (не только для доказательств).

Источник

Верно ли: Любые равносторонние треугольники подобны?

Укажите, верно ли высказывание? Любые равносторонние треугольники подобны?

Собственно так гласит «решебник» за 9-й класс,

А вот сами признаки подобия:

Исходя из 2-го признака можем заключить что любые равносторонние прямоугольники будут подобны, поскольку их стороны будут всегда пропорциональны.

Или же исходя из 3-го признака (углы в равностороннем треугольнике всегда под 60 градусов) и стороны пропорциональны.

Мне эта задачка знакома с детства. Разгадка ее состоит в том, чтобы выйти за границы привычного, двухмерного мышления в отношении выкладывания фигур из спичек на столе.

Ведь как бы мы ни старались раскладывать спички по плоскости так и сяк, не получается выложить четыре равносторонних треугольника из шести спичек. А вот если из плоскости выйти в трехмерное пространство.

Нашлось, действительно двадцать четыре треугольника. Пришлось слегка потрудиться, чтобы уж наглядно предъявить их. Дарю, может кому и понадобится. Чего не сделаешь ради вопрошающих? В общем, двадцать четыре штуки, включая основной из задания.

Не совсем поняла, какие именно треугольники, но могу поделиться рецептом вкусного домашнего печенья «Треугольники».

Затем тесто отправляем на 1-2 ч в холодильник. Достаем, делим на 2 части, чтобы было удобнее работать.Раскатываем одну часть, нарезаем квадратиками, в цент кладем немного сахара, складываем пополам и по краю защепляем пальцами или подходящей палочкой. Затем выпекаем на противне в духовке при температуре 220 градусов, до того как они немножко подрумянятся.

Вместо треугольников из этого теста можно сделать рогалики(типа круасанов, но более завернутые). Для этого раскатанный в круг кусок теста толщиной 1 мм нужно разрезать снежинкой, т.е. сначала пополам, потом провести перпендикулярную линию, чтобы получился крест, и порезать аналогично, чтобы вышла снежинка. В центр толстого конца положить сахар и закатать рулетиком от толстого конца к тонкому. Когда они испекутся, то приобретут объем и будут выглядеть лучше, чем когда только их сделаешь.

Первая задача. Обозначим заданную точку буквой S, а вершины треугольника А, В, С. Из точки S на плоскость треугольника опустим перпендикуляр SO и наклонные SА, SВ и SС. Их проекции на плоскость треугольника соответственно ОА, ОВ и ОС. Если из одной точки к плоскости проведены равные наклонные SА, SВ и SС, то и их проекции ОА, ОВ и ОС тоже равны между собой. Таким образом точка О является центром описанной окружности.

Сторона треугольника, вписанного в окружность, в √3 раз больше радиуса окружности. Значит радиус окружности (ОА, ОВ и ОС) равен 3/√3=√3 см. Теперь из прямоугольного треугольника SOA по Пифагору определяем SO=√(2^2-(√3)^2)=√(4-3)=√(1)=1 см.

Вторая задача. В треугольниках АОВ и АОС углы АВЩ и АСЩ равны по 30°. Катет треугольника, лежащий против угла в 30° (АО) равен половине гипотенузы. Значит гипотенузы АВ и АС равны 20 см. Треугольник АВС прямоугольный равнобедренный. По Пифагору АС=√(20^2+20^2)=√(800)=20√2 см.

Источник

Геометрия

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Пропорциональные отрезки

Если известна длина двух отрезков, то можно узнать, во сколько раз один из них больше другого. Например, если некоторый отрезок NM = 24 см, а другой отрезок KP = 4 см, то можно утверждать, что NM в 6 раз длиннее, так как

Величину NM/KP именуют отношением отрезков NM и KP. Надо заметить, что в ряде случаев отношение отрезков можно найти, не зная их длины. Пусть в ∆МКР проведена медиана МН. Очевидно, что отрезок КР будет вдвое длиннее КН, ведь Н – середина КР:

Другой пример – это отношение между диагональю квадрата и его стороной.

Используя теорему Пифагора, несложно показать, что в любом квадрате АВСD

Наконец, в прямоугольном треуг-ке, один из углов которого равен 30°, гипотенуза всегда вдвое длиннее меньшего из катетов:

Если отношение отрезка AB к А₁В₁ равно отношению отрезка СD к С₁D₁, то говорят, что отрезки AB и CD пропорциональны отрезкам А₁В₁ и С₁D₁. Например, пусть

Получается, AВ и CD пропорциональны А₁В₁ и С₁D₁. Важно отметить, что пропорциональны могут быть также сразу три и более отрезка.

Определение подобных треугольников

В жизни нередко можно наблюдать объекты, у которых совпадает форма, но отличаются размеры. В качестве примера можно привести мяч для настольного тенниса и баскетбольный мяч. Оба этих предмета имеют форму шара, на баскетбольный мяч значительно больше. Другой пример – настоящий танк и игрушка, изображающая его. Часто подобны друг другу матрешки, которые вкладываются друг в друга – все они выглядят одинаково, а отличаются только общим размером. Наконец, подобны и знаменитые египетские пирамиды:

Такие объекты в геометрии именуют подобными. Подобны друг другу любые две окружности и любые два квадрата. Но особо важную роль в геометрии играют подобные треугольники. Рассмотрим это понятие подробнее.

Пусть есть два треуг-ка, ∆AВС и ∆А₁В₁С₁, у которых соответственно равны углы:

Стороны, которые лежат против одинаковых углов в таких треуг-ках, именуют сходственными. Ими являются стороны AВ и А₁В₁, ВС и В₁С₁, АС и А₁С₁.

Можно дать такое определение подобных треугольников:

Таким образом, подобие треугольников (оно обозначается символом ∾) обозначает выполнение сразу нескольких равенств:

Отношение между сходственными сторонами подобных треуг-ков именуется коэффициентом подобия и обозначается буквой k:

Грубо говоря, подобие треуг-ков означает, что их форма одинакова, но один из них в несколько раз больше или меньше другого. Чтобы получить, из одного треуг-ка другой, равный ему по размерам, его надо просто «масштабировать». Например, на этом рисунке все стороны исходного треуг-ка просто увеличили в три раза:

Это значит, что коэффициент подобия в данном случае равен 3. Однако важно понимать, что в различных геометрических задачах подобные треуг-ки также могут быть повернуты друг относительно друга:

Задание. ∆AВС подобен ∆DEF. Известно, что

Найдите длину ЕF.

Решение. Как только в задаче появляются подобные треуг-ки, стоит сразу же определить их коэффициент подобия, а для этого надо разобраться, какие стороны будут сходственными. Так как∠А = ∠Е, то лежащие против них стороны DF и ВС– сходственные. Их отношение и будет равно коэффициенту подобия:

Получили, что стороны ∆DEF вдвое длиннее сходственных им сторон ∆AВС. У подобных треуг-ков углы одинаковы, поэтому∠С = ∠D. Отсюда следует, что стороны AВ и ЕF сходственны, а потому ЕF вдвое больше:

Задание. ∆AВС и∆DEF – подобные. Известно, что

Найдите длину ЕF.

Решение. По сравнению с предыдущей задачей изменилось только одно условие, теперь∠А = ∠D. Однако это меняет сходственные стороны. Из подобия треуг-ков следует, что∠С = ∠Е. Тогда сходственными оказываются уже стороны AВ и DF. Найдем коэффициент подобия треугольников:

Сходственными являются также стороны ВС и ЕF (ведь∠А = ∠D), поэтому ЕF в 1,25 раза длиннее:

Эти две задачи показывают, как важно правильно определять сходственные стороны подобных треугольников.

Естественно, что все равные друг другу треуг-ки являются одновременно и подобными, причем их коэффициент подобия равен единице.

Задание. Докажите, что у подобных треуг-ков отношение их периметров равно коэффициенту подобия.

Решение. Пусть подобны ∆ AВС и ∆А₁В₁С₁, причем

Периметр ∆AВС можно вычислить так:

Мы доказали утверждение, сформулированное в условии.

Первый признак подобия треугольников

Оказывается, для того, чтобы доказать подобие треуг-ков, не требуется сравнивать все их углы и находить соотношение всех сторон. Существуют три простых признака подобия треугольников.

Однако прежде, чем сформулировать их, нам придется доказать отдельное утверждение, которое известно как обобщенная теорема Фалеса («обычную», не обобщенную теорему мы уже изучали ранее).

Если прямые ВВ₁ и СС₁ (показаны красным цветом)параллельны, то отрезки AВ и АС пропорциональны отрезкам AВ₁ и АС₁, то есть справедливо соотношение:

Доказывать будем от противного. Пусть отрезки AВ и АС непропорциональны AВ₁ и АС₁. Тогда отметим наАС такую точку Н, которая разобьет АС на пропорциональные отрезки, то есть

Естественно, эта точка не будет совпадать с С₁. Рассмотрим случай, когда она окажется правее, чем С₁:

Теперь поступим следующим образом. Проведем через стороны угла большое число прямых, параллельных ВС, которые будут разбивать АС на одинаковые отрезки. По теореме Фалеса эти же прямые отсекут одинаковые отрезки и на AВ. При этом мы проведем настолько много параллельных прямых, что хотя бы одна из них пересечет отрезок С₁Н:

Пусть эта прямая пересечет отрезок С₁Н в некоторой точке С₂, а сторону AВ в точке В₂. Ясно, что отрезки AВ и АВ₂ пропорциональны отрезкам АС и АС₂, так как они состоят из одинакового количества одинаковых отрезков. Например, на построенном рисунке отношение AB₂ к AB равно 5/8, так как AB₂ состоит из 5 отрезков, отсеченных зелеными параллельными прямыми, а AB состоит из 8 таких отрезков. Аналогично и отношение АС₂ к АС также равно 5 к 8. Таким образом, можно записать:

Здесь мы рассмотрели случай, когда точка Н лежит правее С₁, то есть АН >C₁. Случай, когда АН 2 раз. Докажем это.

Пусть ∆AВС и ∆А₁В₁С₁ подобны с коэффициентом подобия k. Снова проведем в них высоты СН и СН₁:

Запишем очевидные равенства:

В итоге получили, что площади подобных треугольников отличаются в k 2 раз.

Задание. Известно, у ∆AВС площадь составляет 10, а отрезок AВ имеет длину 5. ∆DEF подобен ∆AВС, причем сторона DE, сходственная AВ, равна 15. Вычислите площадь ∆DEF.

Решение. По условию задачи легко найти коэффициент подобия ∆AВС и ∆DEF, надо лишь поделить одну сходственную сторону на другую:

Решение. Зная площади треуг-ков, легко найдем коэффициент их подобия:

Если коэффициент равен 2, то стороны первого многоугольника вдвое меньше сторон второго, поэтому интересующая нас сторона равна

Источник

Верно ли что все равносторонние треугольники подобны

Признака подобия треугольников

Две фигуры `F` и `F’` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры `F` и `F’` подобны, то пишется `F

F’`. Напомним, что запись подобия треугольников `Delta ABC

Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если `Delta ABC

Delta A_1B_1C_1`, то `/_ A = /_ A_1`, `/_ B = /_ B_1`, `/_ C = /_ C_1`,

`A_1B_1 : AB = B_1C_1 : BC = C_1A_1 : CA`.

Два треугольника подобны, если:

1. два угла одного соответственно равны двум углам другого;

2. две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;

3. три стороны одного треугольника пропорциональны трём сторонам другого.

В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно.

Если две стороны треугольника пересекает прямая, параллельная третьей стороне (рис. 9), то она отсекает треугольник, подобный данному.

Действительно, из параллельности `MN` и `AC` следует, что углы `1` и `2` равны. Треугольники `ABC` и `MBN` имеют два равных угла: общий угол при вершине `B` и равные углы `1` и `2`. По первому признаку эти треугольники подобны.

И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции.

Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках `M` и `N`. Найти длину отрезка `MN`, если основания трапеции равны `a` и `b`.

Delta COB` по двум углам (рис. 10б):

`(OD)/(OB) = (AD)/(BC)`, то есть `(OD)/(OB) = a/b`.

3. Учитывая, что `BD = BO + OD` находим отношение

`(BO)/(BD) = (BO)/(BO + OD) = 1/(1 + OD//BO) = b/(a + b)`.

Подставляя это в (1), получаем `MO = (ab)/(a + b)`; аналогично устанавливаем, что `ON = (ab)/(a + b)`, таким образом `MN = (2ab)/(a + b)`.

Delta MBF`. Из подобия следует `(AE)/(MF) = (AM)/(MB) = 1/3`.

Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон. Верно также следующее утверждение: отношение медиан, биссектрис и высот, проведённых к сходственным сторонам в подобных треугольниках, равно отношению сходственных сторон.

Отношение радиусов вписанных окружностей, как и отношение радиусов описанных окружностей, в подобных треугольниках также равно отношению сходственных сторон.

Попытайтесь доказать это самостоятельно.

Прямоугольные треугольники подобны, если:

1. они имеют по равному острому углу;

2. катеты одного треугольника пропорциональны катетам другого;

3. гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого.

Два первых признака следуют из первого и второго признаков подобия треугольников, поскольку прямые углы равны. Третий признак следует, например, из второго признака подобия и теоремы Пифагора.

Заметим, что высота прямоугольного треугольника, опущенная на гипотенузу, разбивает его на два прямоугольных треугольника, подобных между собой и подобных данному. Доказанные в § 1 метрические соотношения Свойств 1, 2, 3 можно доказать, используя подобие указанных треугольников.

СВОЙСТВА ВЫСОТ И БИССЕКТРИС

Если в треугольнике `ABC` нет прямого угла, `A A_1` и `BB_1` — его высоты, то `Delta A_1B_1C

Delta ABC` (этот факт можно сформулировать так: если соединить основания двух высот, то образуется треугольник, подобный данному).

Как всегда, полагаем `AB = c`, `BC = a`, `AC = b`.
а) Треугольник `ABC` остроугольный (рис. 12а).

В треугольниках `A_1 B_1C` и `ABC` угол `C` общий, прилежащие стороны пропорциональны: `(A_1C)/(AC) = (B_1C)/(BC) = cos C`.

Таким образом, `Delta A_1 B_1 C

$$\left.\begin
\Delta AA_1C, \angle A_1 =90^\circ \Rightarrow A_1C=AC\cdot \cos C =b \cos C;\\
\Delta BB_1C, \angle B_1 =90^\circ \Rightarrow B_1C=BC\cdot \cos C =a \cos C,
\end
\right\>\Rightarrow \Delta A_1B_1C\sim \Delta ABC,$$

коэффициент подобия `ul (cos C)`, `/_ A_1 B_1 C = /_B`.

$$\left.\begin
\Delta AA_1C, \angle A_1 =90^\circ \Rightarrow A_1C=AC\cdot \cos\varphi =b |\cos C|;\\
\Delta BB_1C, \angle B_1 =90^\circ \Rightarrow B_1C=BC\cdot \cos\varphi =b |\cos C|,
\end
\right\>\Rightarrow \Delta A_1B_1C\sim \Delta ABC$$

с коэффициентом подобия `ul (k = |cos C|`, `(/_A_1B_1C=/_B)`.

В остроугольном треугольнике `ABC` проведены высоты `A A_1`, `B B_1`, `C C_1` (рис. 13).

Треугольник, вершинами которого служат основания высот, называется «высотным» треугольником (или ортотреугольником).

Доказать, что лучи `A_1 A`, `B_1 B` и `C_1 C` являются биссектрисами углов высотного треугольника `A_1 B_1 C_1` (т. е. высоты остроугольного треугольника являются биссектрисами ортотреугольника).

По первой лемме о высотах `Delta A_1 B_1 C

Delta ABC`, `/_ A_1 B_1 C = /_ B`.

Аналогично `Delta AB_1C_1

Delta ABC`, `/_ AB_1 C_1 = /_ B`, т. е. `/_A_1 B_1C = /_ AB_1 C_1`.

Высоты `A A_1`, `B B_1` треугольника `ABC` пересекаются в точке `H` (рис. 14). Доказать, что имеет место равенство `AH * H A_1 = BH * HB_1`, т. е. произведение отрезков одной высоты равно произведению отрезков другой высоты.

Delta BHA_1`, имеют по равному острому углу при вершине `H` (заметим, что этот угол равен углу `C`). Из подобия следует `(AH)/(BH) = (HB_1)/(HA_1)`, откуда `AH * HA_1 = BH * HB_1`. Для тупоугольного треугольника утверждение также верно. Попробуйте доказать самостоятельно.

Высоты `A A_1` и `B B_1` треугольника `ABC` пересекаются в точке `H`, при этом `BH = HB_1` и `AH = 2 HA_1` (рис. 15). Найти величину угла `C`.

Установим ещё одно свойство биссектрисы угла треугольника.

Биссектриса треугольника делит одну из сторон треугольника на отрезки длиной `3` и `5`. Найти в каких пределах может изменяться периметр треугольника.

По свойству биссектрисы `AB : AC = 3:5`. Положим `AB = 3x`, тогда `AC = 5x`. Каждая сторона треугольника должна быть меньше суммы двух других сторон, т. е. `ul (5x 1`.

Периметр треугольника `P = 8 + 8x = 8(1 + x)`, поэтому `ul (16

Источник