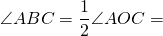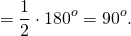верно ли что вписанный угол опирающийся на диаметр окружности прямой

Вписанный угол опирающийся на диаметр окружности прямой

Здравствуйте!
Помогите разобраться, какое из следующих утверждений верно?
1) вписанный угол, опирающийся на диаметр окружности, прямой;
2) если 3 угла в одном треугольнике соответственно равны трем углам в другом треугольнике, то эти треугольники являются равными.
Спасибо!

Утверждение №1.
Вписанный угол, опирающийся на диаметр окружности, прямой.

Ответ.
Утверждение является верным.
Так как рассматриваемый угол является вписанным в окружность и опирается на дугу, равную 180 градусов (диаметр можно рассматривать как развернутый угол с вершиной в центре окружности, равный 180 градусов). Следовательно, такой угол будет равен половине градусной меры этой дуги, а значит, равен 180 / 2 = 90 градусов.
Существует также теорема о плоском угле, который опирается на диаметр окружности, которая называется теоремой Фалеса. Причем эта теорема является частным случаем свойств вписанного угла.
При использовании свойства угла, который опирается на диаметр, возможно выполнить построение касательной к окружности.

Утверждение №2.
Если 3 угла в одном треугольнике соответственно равны трем углам в другом треугольнике, то эти треугольники являются равными.

Ответ.
Утверждение является неверным.
Если у двух треугольников соответственно равны все три угла, то в таком случае треугольники являются подобными, а не равными между собой. Это следует из признаков подобия треугольников, которых всего три. Не стоит путать равенство и подобие треугольников.

Источник

Вписанный угол, опирающийся на диаметр

Вписанный угол, опирающийся на диаметр, обладает полезным свойством, вытекающим из теоремы о вписанном угле.

Свойство вписанного угла, опирающегося на диаметр

(следствие из теоремы о вписанном угле)

Вписанный угол, опирающийся на диаметр, прямой.

Дано:

Так как AC- диаметр, то ∠AOC=180º.

∠AOC — центральный, ∠ABC — соответствующий ему вписанный угол.

Следовательно, по теореме о вписанном угле,

Что и требовалось доказать.

Из этого следует, например, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой.

Если центр описанной окружности лежит на диагонали четырехугольника, то угол напротив этой диагонали — прямой.

Другой вариант формулировки следствия:

Диаметр виден из любой точки окружности под углом 90º.

Если вписанный угол связать с дугой, то следствие из теоремы о вписанном угле звучит так:

Вписанный угол, опирающийся на полуокружность — прямой.

Источник

Центральные и вписанные углы

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, что и вписанный угол.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

Угол AOC и угол ABC, вписанный в окружность, опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Хорда — отрезок, соединяющий две точки на окружности.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Как решаем: окружность 360° − ⌒AC − ⌒CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ ⌒AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ ⌒AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

⌒СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от ⌒CB = 72° / 2 = 36°

Источник

Углы, связанные с окружностью

Вписанные и центральные углы

Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

Теоремы о вписанных и центральных углах

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу равны.

Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Теоремы об углах, образованных хордами, касательными и секущими

Фигура	Рисунок	Теорема
Вписанный угол

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами
Угол, образованный секущими, которые пересекаются вне круга
Угол, образованный касательной и хордой, проходящей через точку касания
Угол, образованный касательной и секущей
Угол, образованный двумя касательными к окружности

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Доказательства теорем об углах, связанных с окружностью

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

что и требовалось доказать.

что и требовалось доказать.

что и требовалось доказать

что и требовалось доказать.

Источник

Верно ли что вписанный угол опирающийся на диаметр окружности прямой

Какие из следующих утверждений верны?

1) Через любые три точки проходит не более одной окружности.

2) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.

3) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.

4) Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Через любые три точки проходит не более одной окружности.» — верно, Через любые три точки, не лежащие на одной прямой, проходит единственная окружность. Если точки лежат на одной прямой, то окружность провести невозможно. Тем самым, через любые три точки можно провести не более одной окружности.

2) «Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.» — верно, если расстояние от центра до прямой меньше радиуса, то окружности имеют две общие точки, если окружности касаются то окружности имеют одну общую точку, если расстояние больше радиуса, то окружности не имеют общих точек.

3) «Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются» — неверно, окружность, радиус которой равен 3, лежит внутри окружности с радиусом 5.

4) «Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.» — верно, вписанный угол измеряется половиной дуги,на которую он опирается.

Источник

• ← вакцина гам ковид вак что нельзя делать после прививки
• полис нового образца номер где →

Угол, образованный пересекающимися хордами хордами

Формула: