верно ли что сумма простых чисел есть число простое

Может ли сумма двух простых чисел быть простым числом?

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37.

Простым числом считается число, которое возможно разделить только на себя и на единицу. В поисках простых чисел сразу обращаем взгляд на нечетные числа, но не все из них являются простыми. Единственным простым четным числом является два.

Как мы видим все простые числа нечетные, а для получения в сумме нечетного числа слагаемые должны быть четное + нечетное. Получается, что для получения в сумме двух простых чисел простого числа надо прибавить простое число к 2.

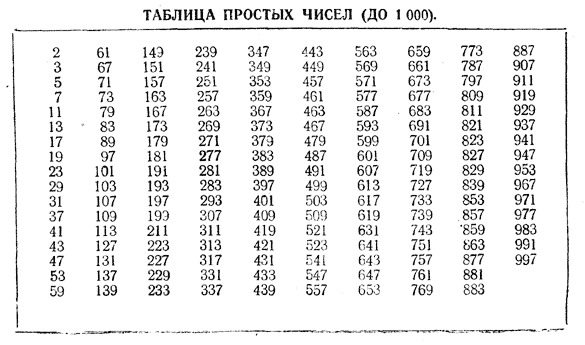
Как бы это не показалось странным, но два простых числа в сумме вполне могут дать еще одно простое число. Казалось бы при сложении двух нечетных чисел должно получиться четное и таким образом уже не нечетное, но кто сказал, что простое число обязательно нечетное? Не будем забывать, что к простым числам относится и число 2, которое делится только на себя и единицу. И тогда оказывается, что если между двумя соседними простыми числами разница 2, то прибавляя к меньшему из них простому числу другое простое число 2 мы получаем большее простое число этой пары. Примеры перед вами:

Есть и другие пары, которые несложно найти в таблице простых чисел по описанному способу.

Простое число, это число которое делится на себя и на 1

Оно положительное и больше единицы

Есть таблицы этих чисел

Есть много статей по этим числам

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37.

Наверное это все числа с разницей в 2

Конечно, ответ на этот вопрос был бы отрицательным, если бы не вездесущая двойка, которая как оказывается, тоже является простым числом.А ведь она подпадает под правило простых чисел:делится на 1 и на самоё себя.И вот из-за неё и ответ на вопрос становится положительным.Множество простых чисел и двойки даёт тоже простое число.Иначе бы все остальные в сумме давали бы число чётное, что является (кроме 2) числами не простыми.О так с 2-ё получаем целый ряд тоже простых чисел.

И как видно из приведённых в литературе таблиц простых чисел, такую сумму с помощью двойки и простого числа можно получить не всегда, а только идёт подчинение некоторому закону.

Из школьного курса математики мы знаем. что сумма двух простых чисел также может быть простым числом. Например 5+2=7 и т.п. Простым же называется то число, которое может делиться на само себя или же ни цифру один. То есть таких чисел довольно много и всоей сумме они также могут давать простое число.

К простым числам относятся те, которые делятся на себя и на единицу.

прилагаю таблицу с простыми числами до числа 997

теперь находим сумму двух простых чисел, чтобы в итоге было тоже простое, с таблицей это сделать будет проще:

Сумма двух простых чисел может быть простым числом только при одном условии: если одно слагаемое является простым числом большим двух, а другое равно, обязательно, цифре два.

Перед тем, как на такой вопрос ответить, нужно подумать, а не сходу отвечать. Так как многие забывают о том, что есть одно чётное число, при это оно является простым. Это число 2. И благодаря ему ответ на вопрос автора: «да!», такое вполне возможно, причём примеров такого довольно много. К примеру 2+3=5, 311+2=313.

Может ли сумма двух простых чисел быть простым числом?

Если учесть то, что простое число-которое можно поделить на само себя, на такое же и на 1.

То-да, может.Простой пример 2+3=5 или 2+5=7

и 5 и 7 делятся на самих себя, и на 1.

Все очень просто, если вспомнить школьные годы.

Если исключить из простых число 2, то сумма двух других чисел не может быть простым числом, поскольку эта сумма будет делиться на 2.

Подобрать простые числа можно по таблице ниже. Зная определение, что называется простым числом, можно подобрать сумму простых чисел, которые дадут тоже простое число. То есть конечная цифра (простое число)будет делиться на себя и на цифру один. Например, два плюс три равно пять. Эти три цифры стоят первыми в таблице простых чисел.

Вариантов ответа на этот вопрос действительно много. например можно переформулировать данную задачу так: Из каких слагаемых состоит сумма равная 350, если одно слагаемое больше второго в 9 раз.

Это очень простая задача, которая решается безо всяких уравнений.

Сумма = МС + 9*МС = 10 МС.

Найти меньшее слагаемое тогда просто: 350/10=35.

Получили, что одно слагаемое равно 35, а второе тогда равно 350-35=315.

Ответ: слагаемые 35 и 315 дают в сумме 350, а слагаемое 315 в 9 раз больше слагаемого 35.

Моя дочка умненькая, и память у неё хорошая, а термины «сумма» и «разность» ей тоже никак не давались, путала и всё тут. Пришлось мне ей помочь.

Kozma of Szechwan, вы невнимательны. Сказано не сумма всех чисел, а сумма простых чисел.

Василий правильно написал у вас в комменте:

2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29 + 31 + 37 = 197

Сложение, наряду с вычитанием, умножением и делением является одним из простейших арифметических действий.

Пожалуй, именно со сложения стоит начинать знакомство с математическими действиями.

Под сложением понимают объединение двух и более объектов, предметов, чисел в единое целое.

Например, если к одному яблоку добавить два яблока, мы получим три яблока: 1 + 2 = 3.

Те объекты ( числа ), которые складываются ( объединяются ), называются слагаемыми. Слагаемых может быть в примере два и больше. То есть количество слагаемых может быть любым, но оно должно быть не меньше двух.

Действие сложение обозначается знаком ( символом ) «+» ( плюс ).

Важно знать, что от перестановки слагаемых местами сумма не меняется: 1 + 2 = 3 и 2 + 1 = 3.

Примеры на сложение можно читать по-разному:

Все приведенные формулы и понятия сложение, вычитание, умножение, деление не что иное как арифметические действия, которыми мы пользуемся в своей повседневной жизни весьма и весьма часто.

Понятие сложение практически не нуждается в определении, поскольку вытекает из простых фактов, и не может быть определено формально.

В результате сложения чисел получается сумма, а сами складываемые числа называются слагаемыми.

Умножение, в результате которого получается произведение, позволяет повторить некоторое число а (это множимое) слагаемым столько раз, сколько указывает другое число в (множитель). Если множимое и множитель поменять местами, то произведение от этой перестановки не изменится. Поэтому множитель и множимое и называют сомножителями.

Источник

Что такое Простые числа

Простые числа — это натуральные числа, больше единицы, которые делятся без остатка только на 1 и на само себя. Например: 2, 3, 5, 7, 11, 13, 17, 19, 23. Единица не является ни простым числом, ни составным.

Последовательность простых чисел начинается с 2 и является бесконечной; наименьшее простое число — это 2 (делится на 1 и на самого себя).

Составные числа — это натуральные числа, у которых есть больше двух делителей (1, оно само и например, 2 и/или 3); это противоположность простым числам. Например: 4, 6, 9, 12 (все делятся на 2, на 3, на 1 и на само себя).

Все натуральные числа считаются либо простыми, либо составными (кроме 1).

Натуральные числа — это те числа, которые возникли натуральным образом при счёте предметов; например: 1, 2, 3, 4. (нет ни дробей, ни 0, ни чисел ниже 0).

Зачастую множество простых чисел в математике обозначается буквой P.

Простые числа до 1000

Как определить, является ли число простым?

Очень простой способ понять, является ли число простым — нужно его разделить на простые числа и посмотреть, получится ли целое число. Сначала нужно попробовать его разделить на 2 и/или на 3. Если получилось целое число, то оно не является простым.

Если после первого деления не получилось целого числа, значит нужно попробовать разделить его на другие простые числа: 5, 7, 11 и т. д. (на 9 делить не нужно, т. к. это не простое число и оно делится на 3, а на него вы уже делили).

Более структурированный метод — это решето Эратосфена.

Решето Эратосфена

Это алгоритм поиска простых чисел. Для этого нужно:

Те числа, которые не будут вычеркнуты в конце этого процесса, являются простыми.

Взаимно простые числа

Это натуральные числа, у которых 1 — это единственный общий делитель. Например:

Число Мерсенна

Простое число Мерсенна — это простое число вида:

До 1536 г. многие считали, что числа такого вида были все простыми, пока математик Ульрих Ригер не доказал, что 2 (^11) – 1 = 2047 было составным (23 x 89). Затем появились и другие составные числа (p = 23, 29, 31, 37 и др.).

Например, для p = 23 это 2 (^23) – 1 = 8 388 607; И 47 x 178481 = 8 388 607, значит оно составное.

Почему 1 не является простым числом?

Российские математики Боревич и Шафаревич в своей знаменитой работе «Теория чисел» (1964 г.) определяют простое число как p (элемент кольца D), не равен ни 0, ни 1. И p можно называть простым числом, если его невозможно разложить на множители ab (т.е. p = ab), притом ни один из них не является единицей в D. Так как 1 невозможно представить ни в одном, ни в другом виде, 1 не считается ни простым числом, ни составным.

Почему 4 не является простым числом?

Простое число — это натуральное число, больше единицы, которое делится без остатка на 1 и на само себя. Т. к. 4 можно разделить на 1, на 2 и на 4, из-за деления на 2 оно не является простым.

Самое большое простое число

21 декабря 2018 года Great Internet Mersenne Prime Search (проект, целью которого является открытие новых простых чисел Мерсенна) обнаружил новое самое большое известное простое число:

Новое простое число также именуется M82589933 и в нём более чем на полтора миллиона цифр больше, чем в предыдущем (найденном годом ранее).

Источник

Закономерности в распределении простых чисел

Введение

Простое число — это натуральное число, имеющее ровно два различных натуральных делителя — единицу и самого себя. Такие числа представляют огромный интерес. Дело в том, что никто так и не смог полностью понять и описать закономерность по которой простые числа располагаются в ряду натуральных чисел.

Ещё до нашей эры Евклид сформулировал и доказал первые теоремы о простых числах. С тех пор математики, среди них Гаусс, Ферма, Риман, Эйлер, продолжали исследования и надо отдать им должное заметно продвинулись. Было обнаружено много интересных свойств простых чисел, выдвинуто много предположений, некоторые из которых были доказаны. Однако много гипотез связанных с простыми числами до сих пор остаются необоснованными.

Распределение простых чисел

Первостепенная задача, решение которой автоматически привело бы к решению большинства вопросов связанных с простыми числами заключается в следующем:

Получить рекуррентную формулу для очередного простого числа

Существует родственная ей задача о количестве простых чисел, не превосходящих заданной величины:

Найти функцию p(x), значение которой в точке x равно числу простых чисел на отрезке [1, x]. Где x – любое действительное число не меньшее единицы.

Функция называется функцией распределения простых чисел.

К решению вышеуказанных задач существует множество подходов. Рассмотрим некоторые из них.

Основная теорема арифметики гласит, что любое натуральное число большее единицы может быть представлено в виде произведения простых множителей (причём единственным образом, с точностью до порядка множителей).

Отсюда и из определения простого числа следует, что натуральное число, большее двух, является простым тогда и только тогда, когда оно не делится ни на одно из простых чисел меньших самого себя.

Первое простое число p₁ =2. Значит все последующие простые числа должны не делится на 2, то есть иметь вид 2k+1, где k – натуральное. То есть все простые числа начиная со второго — нечётные.

Второе простое число p₂ = 3. Значит все последующие простые числа должны иметь вид 3m+1, либо 3m+2, где m – целое. Это равносильно утверждению о том, что все простые числа начиная с третьего не делятся на три. Однако при этом числа ещё должны не делится на два, то есть иметь вид 2k+1.

Решая диофантовы уравнения

найдём k и m и получим, что все простые числа начиная с p₃ обязательно представимы в виде , либо в виде , где t – целое.

И правда, какое бы простое число мы ни взяли оно представимо таким образом:

Однако обратное неверно, то есть любое натуральное число вида 6t+1 или 6t+5 не обязательно простое. Например, .

Третье простое число p₃ = 5. И если по аналогии учесть, что любое простое число, начиная с четвёртого не делится на 5, также не делится на p₁ = 2 и на p₂ = 3, то получим, что все простые числа начиная с p₄ обязательно имеют одно из представлений

Затем учтём p₄, p₅ и т.д. Проблема в том, что на каждом шаге нам придётся решать всё большую систему диофантовых уравнений, поэтому такой прямолинейный подход оказывается весьма сложным.

На самом деле, при различных попытках решения поставленной нами задачи в большом количестве случаев появляются одни и те же конструкции. Например, произведение Эйлера. Рассмотрим, как это происходит, на следующем примере.

Итак, как же найти функцию F(x)? Сначала рассмотрим множество всех натуральных чисел. Какова доля чисел, которые не делятся ни на одно из простых p₁, p₂, …, p_n?

Каждое второе число делится на p₁ = 2. Значит, часть всех чисел делится на p₁.

Каждое третье число делится на 3. Значит, всех чисел делится на p₂. При этом надо учесть, что каждое шестое число делится и на 2 и на 3 одновременно.

Значит, доля чисел не делящихся ни на 2, ни на 3 равна

Если преобразовать выражение, то оно примет вид:

Опять же можно представить выражение в виде

Будем обозначать такое произведение P(n). Кстати, если учесть все простые числа (n→∞), то мы получим обратную величину от так называемого произведения Эйлера.

Почему так происходит? Когда мы получали формулу (1), мы пользовались рассуждениями, что среди всех натуральных чисел доля, делящихся на p_n, равна . Но нельзя сделать такое утверждение о конечном наборе последовательных натуральных чисел. Например, возьмём набор 1,2, 3,4,5,6,7,8,9. Здесь 4 числа из 9 делятся на два. И несложно заметить, что отличается от . То есть, при применении к конечному набору чисел, данный метод даёт результат с некоторой погрешностью.

Это будет мешать далее получать точные формулы. Но если оценить эту погрешность, то можно (например, приняв и используя приведённые выше рассуждения) получить оценку для p_n+1-го простого числа. Однако, получение таких оценок — это тема отдельной работы. И поэтому здесь я не буду на этом останавливаться, а приведу лишь некоторые результаты, полученные математиками.

Одна из оценок для простого числа с номером n:

оценка верна для всех n, начиная с 6.

А вот формула для функции распределения простых чисел:

Для функции Риман получил приближение, используя интегральный логарифм и нетривиальные нули дзета-функции Римана. Однако, это приближение верно, только если верна гипотеза Римана. Причём если гипотеза Римана верна, то оно является наилучшим.

Гипотеза Римана до сих пор не доказана и не опровергнута. Она, как мы могли видеть, тесно связана с простыми числами и, вообще, имеет огромное значение для теории чисел. Из-за своей важной роли в математике, гипотеза Римана была объявлена одной из семи задач тысячелетия.

Проблемы Ландау

Насчёт простых чисел выдвинуто очень много интересных гипотез. Среди них видное место занимают гипотезы Ландау (проблемы Ландау). Формулируются они так:

1. Гипотеза Гольдбаха

Можно ли любое целое чётное число, большее 2, записать в виде суммы двух простых?

2. Гипотеза о числах-близнецах

Бесконечно ли число простых p таких, что p + 2 тоже простое?

3. Гипотеза Лежандра

Всегда ли существует по меньшей мере одно простое число, лежащее между двумя последовательными полными квадратами?

4. Гипотеза о почти квадратных простых числах

Существует ли бесконечно много простых чисел p вида .

Проблемы Ландау ни доказаны, ни опровергнуты по состоянию на 2020 год. Далее кратко расскажу про каждую из них.

1. Гипотеза Гольдбаха

Существуют две гипотезы Гольдбаха: слабая (тернарная) и сильная (бинарная).

Слабая гипотеза Гольдбаха: Каждое нечётное число, большее 5, можно представить в виде суммы трёх простых чисел.

Эту гипотезу доказал Харольд Гельфготт в 2013 году используя так называемые большие дуги. Финальная часть доказательства заняла 133 страницы.

Сильная гипотеза Гольдбаха: Каждое чётное число, большее двух, можно представить в виде суммы двух простых чисел.

Надо заметить, что в обоих случаях гипотезы Гольдбаха простые числа не обязательно должны быть различными.

Заметьте, что в сильной гипотезе речь идёт только о чётных числах. Давайте покажем, что нечётное число не обязано быть представимо в виде суммы двух простых чисел. Просто приведём пример. Число 11 не представимо в виде суммы двух простых. Вроде бы несложно.

Но переформулируем проблему так: существует ли такое число, что любое нечётное, большее этого числа, представимо в виде суммы двух простых чисел? Давайте проверим. Пусть существует некоторое нечётное натуральное число N, такое, что любое нечётное число представимо в виде суммы двух простых чисел.

Возьмём произвольное нечётное . По предположению существуют такие простые p₁ и p₂, что . Если сумма двух натуральных чисел нечётна, то это значит, что одно из слагаемых чётно, а другое нет. Пусть для определённости p₁ – чётное. Единственное чётное простое число — это 2. Значит, . То есть, K-2 (предыдущее перед K нечётное число) является простым. Поскольку всё вышесказанное верно для любого нечётного большего N, то получается, что все нечётные числа, начиная с N-2, являются простыми. Это неверно. Если бы это было так, то при n→ ∞. Однако, как говорилось выше при n→ ∞.

Итак, не существует такого числа, начиная с которого все нечётные числа могут быть представлены в виде суммы двух простых.

А что же насчёт чётных? Гипотеза не была опровергнута, не было найдено ни одного контрпримера. Но это не значит, что их не существует. Доказать же гипотезу полностью пока никому не удалось.

2. Гипотеза о числах-близнецах

Бесконечно ли число простых чисел близнецов?

Для начала сформулируем определение. Два простых числа называются близнецами если отличаются друг от друга на 2.

Так же доказано, что существует бесконечно много простых чисел, разница между которыми составляет 246. Это наилучшая из обоснованных на данный момент оценок. Если же использовать некоторые недоказанные гипотезы о простых числах, то оценку можно улучшить.

3. Гипотеза Лежандра

Всегда ли существует, по меньшей мере, одно простое число, лежащее между двумя последовательными полными квадратами?

Аналогичная гипотеза доказана для кубов, начиная с некоторого n. То есть, существует, по меньшей мере, одно простое число, лежащее между и для достаточно большого n. Для квадратов же, гипотеза Лежандра пока не доказана.

4. Почти квадратные простые числа

Заключение

Как мы видим, в этой области теории чисел существует очень много пробелов, а также недоказанных гипотез. Отдельно хочется сказать про численную проверку утверждений. Например, ни для одной из гипотез Ландау не был найден контрпример, даже с использованием значительных вычислительных мощностей в течение большого времени. Однако, в истории математики 20-го и 21-го века были случаи, когда контрпример, опровергающий гипотезу, был настолько огромным числом, что его не удавалось найти с помощью вычислительных машин.

Также, постоянный интерес к простым числам обусловлен их обширным применением в криптографии. Итак, как мы убедились, исследование простых чисел — это, действительно, важная и очень интересная задача.

Источник

• ← воспалился глаз чем мазать
• что нужно говорить когда звонишь в скорую →