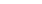в чем заключаются работы при детальной разбивки кривых на местности
Разбивка кривых на местности



Разбивка главных точек кривой. Закрепив на местности вершину угла и предшествующие ему пикеты, закрепляют главные точки кривой.
Середину кривой СК закрепляют, отложив от ВУ по направлению биссектрисы отрезок, равный Б (или Бс).
На новом после вершины угла направлении трассы откладывают величину домера, после чего продолжают разбивку пикетажа. Обеим точкам домера (его началу и концу) присваивают одно и то же пикетажное наименование, благодаря чему пикетаж точки КК совпадает с пикетажем, считаемым по кривой.
Положение начала кривой НК и конца кривой КК определяют, используя разбитый пикетаж. Например, если ПК НК = 5 + 39,27, то от пикета № 5 откладывают вперёд 39,27 м и здесь колышком и сторожком закрепляют точку НК.
Детальная разбивка кривых.При детальной разбивке кривую закрепляют на местности через 10 или 20 м, применяя разные способы.
Способ ординат от касательной для круговой кривой. Для каждой точки i (рис. 15.7, а), задавая расстояние k от начала кривой, вычисляют ее координаты:
Здесь угол j выражен в радианах и равен j = k/R.
Разбивку кривой ведут от ее начала и от конца к середине. Мерной лентой по оси x откладывают длину кривой k, от полученной точки отступают назад на величину k–x и здесь строят перпендикуляр – ординату y. Значения k–x и y обычно выбирают из таблиц для разбивки кривых.
Рис. 15.7 Детальная разбивка кривых:
а – способом ординат от касательной для круговой кривой;
б – то же, для переходной и следующей за ней круговой кривой;
в – разбивка кривой электронным тахеометром
Способ ординат от касательной для переходной и следующей за ней круговой кривой (рис. 15.7, б). Для точек, расположенных в пределах переходной кривой, то есть при k £ l, координаты x, y вычисляют по формулам (15.8) и (15.9), принимая s = k. Для точек i, расположенных на круговой кривой, где k > l, вычисления выполняют по формулам:
Действия при разбивке кривой на местности аналогичны тем, что выполняют при разбивке круговой кривой.
Разбивка кривой с помощью электронного тахеометра. Выбирают на местности такую точку T (рис. 15.7, в), где обеспечена видимость точек будущей кривой и ее начала НК. В точке НК измеряют угол g и расстояние d. Вычисляют координаты точки Т:
По приведенным выше формулам вычисляют координаты точек кривой xi, yi (i = 1, 2, …).
Разбивка кривых на местности.
Середину кривой СК закрепляют, отложив от ВУ по направлению биссектрисы отрезок, равный Б (или Бс).
На новом после вершины угла направлении трассы откладывают величину домера, после чего продолжают разбивку пикетажа. Обеим точкам домера (его началу и концу) присваивают одно и то же пикетажное наименование, благодаря чему пикетаж точки КК совпадает с пикетажем, считаемым по кривой.
Положение начала кривой НК и конца кривой КК определяют, используя разбитый пикетаж. Например, если ПК НК = 5 + 39,27, то от пикета № 5 откладывают вперёд 39,27 м и здесь колышком и сторожком закрепляют точку НК.
Детальная разбивка кривых. При детальной разбивке кривую закрепляют на местности через 10 или 20 м, применяя разные способы.
Способ ординат от касательной для круговой кривой. Для каждой точки i (рис. 15.7, а), задавая расстояние k от начала кривой, вычисляют ее координаты:
Здесь угол j выражен в радианах и равен j = k/R.
Разбивку кривой ведут от ее начала и от конца к середине. Мерной лентой по оси x откладывают длину кривой k, от полученной точки отступают назад на величину k–x и здесь строят перпендикуляр – ординату y. Значения k–x и y обычно выбирают из таблиц для разбивки кривых.
Рис. 15.7 Детальная разбивка кривых:
а – способом ординат от касательной для круговой кривой;
б – то же, для переходной и следующей за ней круговой кривой;
в – разбивка кривой электронным тахеометром
Способ ординат от касательной для переходной и следующей за ней круговой кривой (рис. 15.7, б). Для точек, расположенных в пределах переходной кривой, то есть при k £ l, координаты x, y вычисляют по формулам (15.8) и (15.9), принимая s = k. Для точек i, расположенных на круговой кривой, где k > l, вычисления выполняют по формулам:
Действия при разбивке кривой на местности аналогичны тем, что выполняют при разбивке круговой кривой.
Разбивка кривой с помощью электронного тахеометра. Выбирают на местности такую точку T (рис. 15.7, в), где обеспечена видимость точек будущей кривой и ее начала НК. В точке НК измеряют угол g и расстояние d. Вычисляют координаты точки Т:
По приведенным выше формулам вычисляют координаты точек кривой xi, yi (i = 1, 2, …).
Оставьте свой комментарий
Оставить комментарий от имени гостя
Комментарии
Закрепленные
Понравившиеся
Последние материалы
Заключение (Грунты)
При построении курса учитывалась необходимость его использования для различных гидротехнических специальностей и специализаций. В качестве основной части для студентов всех гидротехнических специальностей следует считать обязательным прочтение гл. 1—7. В гл. 8.
Представления о решении задач нелинейной механики грунтов
На современном этапе развития нелинейного направления механики грунтов оформились два основных подхода к решению практических задач расчета грунтовых оснований и сооружений: нелинейно-упругий и упругопластический (А. К. Бугров, С. С. Вялов.
Прочность грунтов при сложном напряженном состоянии
Для сред и материалов, обладающих сплошностью, предложено много различных условий прочности. Для оценки прочности грунтов наиболее широкое распространение получило условие Мора—Кулона (2.38), не содержащее промежуточного главного напряжения а2 и тем.
Основные закономерности татического деформирования грунтов
За последние 15. 20 лет в результате многочисленных экспериментальных исследований с применением рассмотренных выше схем испытаний получены обширные данные о поведении грунтов при сложном напряженном состоянии. Поскольку в настоящее время в…
Упругопластическое деформирование среды и поверхности нагружения
Деформации упругопластических материалов, в том числе и грунтов, состоят из упругих (обратимых) и остаточных (пластических). Для составления наиболее общих представлений о поведении грунтов при произвольном нагружении необходимо изучить отдельно закономерности…
Описание схем и результатов испытаний грунтов с использованием инвариантов напряженного и деформированного состояний
При исследовании грунтов, как и конструкционных материалов, в теории пластичности принято различать нагружение и разгрузку. Нагружением называют процесс, при котором происходит нарастание пластических (остаточных) деформаций, а процесс, сопровождающийся изменением (уменьшением)…
Инварианты напряженного и деформированного состояний грунтовой среды
Применение инвариантов напряженного и деформированного состояний в механике грунтов началось с появления и развития исследований грунтов в приборах, позволяющих осуществлять двух- и трехосное деформирование образцов в условиях сложного напряженного состояния…
О коэффициентах устойчивости и сопоставление с результатами опытов
Так как во всех рассмотренных в этой главе задачах грунт считается находящимся в предельном напряженном состоянии, то все результаты расчетов соответствуют случаю, когда коэффициент запаса устойчивости к3 = 1. Для…
Давление грунта на сооружения
Особенно эффективны методы теории предельного равновесия в задачах определения давления грунта на сооружения, в частности подпорные стенки. При этом обычно принимается заданной нагрузка на поверхности грунта, например, нормальное давление р(х), и…
Несущая способность оснований
Наиболее типичной задачей о предельном равновесии грунтовой среды является определение несущей способности основания под действием нормальной или наклонной нагрузок. Например, в случае вертикальных нагрузок на основании задача сводится к тому…
Процесс отрыва сооружений от оснований
Задача оценки условий отрыва и определения требуемого для этого усилия возникает при подъеме судов, расчете держащей силы «мертвых» якорей, снятии с грунта морских гравитационных буровых опор при их перестановке, а…
Решения плоской и пространственной задач консолидации и их приложения
Решений плоской и тем более пространственных задач консолидации в виде простейших зависимостей, таблиц или графиков очень ограниченное число. Имеются решения для случая приложения к поверхности двухфазного грунта сосредоточенной силы (В…
Разбивка кривых на местности
Разбивка главных точек кривой. Закрепив на местности вершину угла и предшествующие ему пикеты, закрепляют главные точки кривой.
Середину кривой СК закрепляют, отложив от ВУ по направлению биссектрисы отрезок, равный Б (или Бс).
На новом после вершины угла направлении трассы откладывают величину домера, после чего продолжают разбивку пикетажа. Обеим точкам домера (его началу и концу) присваивают одно и то же пикетажное наименование, благодаря чему пикетаж точки КК совпадает с пикетажем, считаемым по кривой.
Положение начала кривой НК и конца кривой КК определяют, используя разбитый пикетаж. Например, если ПК НК = 5 + 39,27, то от пикета № 5 откладывают вперёд 39,27 м и здесь колышком и сторожком закрепляют точку НК.
Детальная разбивка кривых.При детальной разбивке кривую закрепляют на местности через 10 или 20 м, применяя разные способы.
Способ ординат от касательной для круговой кривой. Для каждой точки i (рис. 15.7, а), задавая расстояние k от начала кривой, вычисляют ее координаты:
Здесь угол j выражен в радианах и равен j = k/R.
Разбивку кривой ведут от ее начала и от конца к середине. Мерной лентой по оси x откладывают длину кривой k, от полученной точки отступают назад на величину k–x и здесь строят перпендикуляр – ординату y. Значения k–x и y обычно выбирают из таблиц для разбивки кривых.
Рис. 15.7 Детальная разбивка кривых:
а – способом ординат от касательной для круговой кривой;
б – то же, для переходной и следующей за ней круговой кривой;
в – разбивка кривой электронным тахеометром
Способ ординат от касательной для переходной и следующей за ней круговой кривой (рис. 15.7, б). Для точек, расположенных в пределах переходной кривой, то есть при k £ l, координаты x, y вычисляют по формулам (15.8) и (15.9), принимая s = k. Для точек i, расположенных на круговой кривой, где k > l, вычисления выполняют по формулам:
Действия при разбивке кривой на местности аналогичны тем, что выполняют при разбивке круговой кривой.
Разбивка кривой с помощью электронного тахеометра. Выбирают на местности такую точку T (рис. 15.7, в), где обеспечена видимость точек будущей кривой и ее начала НК. В точке НК измеряют угол g и расстояние d. Вычисляют координаты точки Т:
По приведенным выше формулам вычисляют координаты точек кривой xi, yi (i = 1, 2, …).
Дата добавления: 2016-01-03 ; просмотров: 1765 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Лекция Разбивка главных точек кривой на местности
Кривые по трассе разбивают, чтобы сгладить резкие повороты трассы, недопустимые для таких сооружений, как усовершенствованные дороги, каналы и некоторые трубопроводы. Разбивка кривой требует от пикетажиста знаний технических условий для устройства сооружения, трассу которого он разбивает. Разбивка кривой в трех главных точках сопровождается введением в измеренную длину трассы поправки Д (домера), а также выносом пикетов на кривую.
По вычисленным элементам круговую кривую разбивают так: от вершины угла отмеряют лентой по трассе в обратном направлении величину тангенса Т и получают точку НК (начало кривой). Отмеряя эту же величину от вершины угла в прямом направлении трассы, получают точку КК (конец кривой). Чтобы получить точку СК (середина кривой), делят на местности при помощи теодолита угол (3 пополам, получают направление биссектрисы этого угла; откладывая по направлению биссектрисы величину Б, получают точку СК. Поправку в длину трассы вводят путем смещения вперед на величину домера следующего за концом кривой пикета, первоначальное положение которого было найдено измерениями по ломаной (по тангенсам).
Профили строят на миллиметровой бумаге. Продольный профиль строят в такой последовательности: 1) строят вспомогательные графы шириной от 0,5 до 2 см в соответствии с потребностью расположить в них записи или чертежи; 2) заполняют графы, начиная с графы расстояний, предварительно разбитой на интервалы согласно горизонтальному масштабу и расстоянию между пикетными точками и между пикетными и плюсовыми точками; расстояния между смежными точками на профиле подписывают только в случае, когда имеются плюсовые точки; 3) подписывают номера пикетных точек; 4) в графу «фактические отметки» * вписывают отметки пикетов и плюсовых точек, взятые из журнала геометрического нивелирования по трассе; 5) в графе «план полосы по трассе» строят ситуацию полосы местности вдоль трассы, снятую при разбивке пикетажа, причем сама трасса изображается в виде прямой линии посередине графы; 6) выбирают Яуг — отметку условного горизонта, от которой следует строить вертикальный разрез трассы; для удобства вычислений и построений профиля отметка условного горизонта выбирается кратной 10 м, и, кроме того, она должна позволить построить разрез по трассе, необходимой для проектирования сооружения глубины; 7) от линии условного горизонта вверх в вертикальном масштабе профиля откладывают разность отметок — фактической (черной) и условного горизонта над каждым пикетом и плюсовой точкой профиля и находят положение этих точек на разрезе; далее от найденных точек до линии условного горизонта проводят «ординаты», а смежные точки соединяют между собой прямыми линиями, которые по совокупности образуют ломаную линию, изображающую линии поверхности земли по трассе; 8) оформляют профиль, т. е. подписывают наименование трассы, масштабы профиля, даты производства изысканий по трассе. На построенном «черном профиле» проектируют сооружение, ось которого изображают линией красного цвета — проектной линией. В одной из граф профиля подписывают проектный уклон оси сооружения, в другой — проектные (красные) отметки точек оси; около проектной линии подписывают «рабочие отметки», выражающие проектные высоты насыпи или глубины выемки в разных точках трассы.
Поперечные профили строят в одном масштабе для горизонтальных и вертикальных расстояний. Такой неискаженный чертеж удобен для проектирования насыпей и выемок по направлению трассы и, в частности, для определения планиметром площадей поперечных сечений, а следовательно, и для подсчета объемов насыпей и выемок. Число и содержание вспомогательных граф на поперечном профиле могут быть различными в зависимости от вида сооружения; однако на любом поперечном профиле подписывают: 1) наименование точек поперечника; 2) фактические отметки точек поперечного профиля, включая и отметку точки пересечения его с трассой; 3) расстояния от трассы до точек поперечного профиля; 4) проектные и рабочие отметки.
Середину кривой СКК закрепляют, отложив от ВУ по направлению биссектрисы угла, образованного направлениями трассы, отрезок, равный Б.
Рис. 1. Разбивка пикетажа с учетом кривой.
Рис. 2.Схема круговой кривой.
1. Зачем разбивают кривые по трассе?
2. Что значит «разбить кривую в главных точках на местности»?
3. Как разбивают круговую кривую?
4. В какой последовательности строят продольный профиль?
5. Что подписывают на любом поперечном профиле?
ДЕТАЛЬНАЯ РАЗБИВКА КРУГОВЫХ КРИВЫХ
Детальная разбивка кривой предусматривает не только закреп-ление на местности начала НК, конца КК и середины СК кривой, но и обозначение всей кривой, например, колышками через определен-ный интервал. Существует ряд способов разбивки круговых кривых: способ прямоугольных координат, способ углов, способ продолжен-ных хорд.
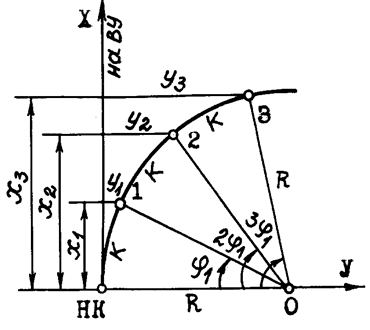
Способ прямоугольных координат (ординат от тангенса).
|
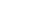
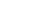

|
|
|
|
|
|
В эти формулы подставляют значение угла j1, зависящее от величины интервала К, которое можно найти из выражения:
j1= 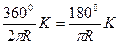
Способ углов (полярный способ).
|
|
|
|
|
Этот способ удобно применять в стесненных условиях, когда есть видимость между НК и точками 1, 2, 3. (например, на высокой насыпи, где способ прямоугольных координат неприемлем).
|
|

|
|
|
|
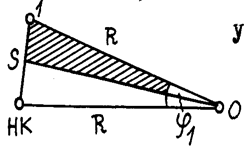
Способ продолженных хорд
|
|
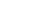



|
|
Недостатком способов углов и продолженных хорд является снижение точности разбивки кривой по мере возрастания ее длины, так как положение каждой последующей точки определяется относительно предыдущей.





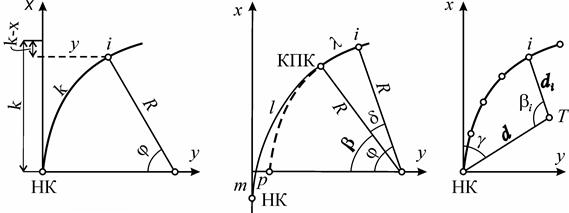



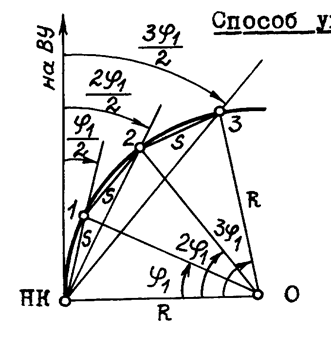
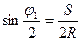 (из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.
(из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.