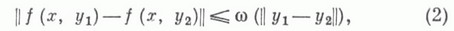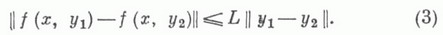в чем заключается задача коши

Инструменты пользователя

Инструменты сайта

Боковая панель

Теория вероятностей и математическая статистика
Строительная механика для строительных специальностей
Матанализ. Дифференциальное и интегральное исчисление
Экономика

Решение дифференциальных уравнений:

Контакты

Решение задачи Коши (диффуры)

Задача Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Что бы решить задачу Коши – нужно получить общее решение дифференциального уравнения в которое входят произвольные постоянные, количество которых зависит от порядка дифференциального уравнения и численно равно этому порядку. Собственно, решение задачи Коши и отличается от нахождения общего решения дифференциального уравнения тем, что, используя общее решение с учётом начальных условий находят эти произвольные константы, входящие в общее решение.

От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.

Примеры

Пример 1.

Решение дифференциального уравнения:

Дифференциальные уравнения с разделяющимися переменными. Решение задачи Коши

Источник

Коши задача

Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.

Основные вопросы, которые связаны с задачей Коши, таковы:

Содержание

Различные постановки задачи Коши

Свойства задачи Коши

См. также

Литература

А.Н. Тихонов, А.Б. Васильева, А.Г. Свешников Курс высшей математики и математической физики. Дифференциальные уравнения. — Физматлит, 2005. — ISBN 5-9221-0277-X

Полезное

Смотреть что такое «Коши задача» в других словарях:

Коши задача — одна из основных задач теории дифференциальных уравнениний. Заключается в нахождении решения такого уравнения, удовлетворяющего так называемым начальным условиям. Например, для уравнения dy = 2xdx можно поставить Коши задачу: найти решение… … Энциклопедический словарь

КОШИ ЗАДАЧА — задача о нахождении решения дифференц. ур ния (обыкновенного или в частных производных), удовлетворяющего нач. условиям. Рассмотрена в 1823 24 О. Коши (A. Cauchy). Примером К. з. может служить осн. задача механики, когда по известным нач.… … Физическая энциклопедия

КОШИ ЗАДАЧА — одна из основных задач теории дифференциальных уравнений. Заключается в нахождении решения такого уравнения, удовлетворяющего т. н. начальным условиям. Напр., для уравнения dy = 2xdx можно поставить Коши задачу: найти решение у = у(х),… … Большой Энциклопедический словарь

КОШИ ЗАДАЧА — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в отыскании решения (интеграла) дифференциального уравнения, удовлетворяющего так наз. начальным условиям (начальным данным). К. з. обычно… … Математическая энциклопедия

Коши задача — одна из основных задач теории дифференциальных уравнений (См. Дифференциальные уравнения), впервые систематически изучавшаяся О. Коши. Заключается в нахождении решения u (x, t); х = (x1. xn) дифференциального уравнения вида: … … Большая советская энциклопедия

КОШИ ЗАДАЧА — численные методы решения для обыкновенного дифференциального уравнения. Задачей Коши наз. задача определения функции или нескольких функций, удовлетворяющих одному или, соответственно, системе дифференциальных уравнений и принимающих заданные… … Математическая энциклопедия

КОШИ ЗАДАЧА — одна из оси. задач теории дифференц. ур ний. Заключается в нахождении решения такого ур ния, удовлетворяющего т. н.начальным условиям. Напр., для ур ния dy = 2xdx можно поставить К. з.: найти решение у = у(х), принимающее при х0 = 0 значение… … Естествознание. Энциклопедический словарь

КОШИ ХАРАКТЕРИСТИЧЕСКАЯ ЗАДАЧА — задача отыскания решения дифференциальных уравнений или систем уравнений с частными производными по заданным его значениям на характеристических многообразиях. Для широкого класса уравнений гиперболического и параболического типов в пространстве… … Математическая энциклопедия

Коши — (Cauchy) Огюстен Луи (21.8.1789, Париж, 23.5.1857, Со), французский математик, член Парижской АН (1816). Окончил Политехническую школу (1807) и Школу мостов и дорог (1810) в Париже. В 1810 13 работал инженером в г. Шербур. В 1816 30… … Большая советская энциклопедия

Источник

КОШИ ЗАДАЧА

численные методы решения для обыкновенного дифференциального уравнения. Задачей Коши наз. задача определения функции или нескольких функций, удовлетворяющих одному или, соответственно, системе дифференциальных уравнений и принимающих заданные значения в нек-рой фиксированной точке. Пусть

Вводя соответствующим образом новые неизвестные функции, можно привести к такому виду К. з. для любой системы обыкновенных дифференциальных уравнений произвольного порядка. Решение задачи (1) существует, если функция f(x, у).непрерывна в П. Для того чтобы это решение было единственным, достаточно, чтобы выполнялось условие О т к у д а:

или более сильное условие Липшица:

Величина Lназ. постоянной Липшица. Если функция f(x, у).непрерывно дифференцируема по у, то в качестве постоянной Липшица можно взять величину

В точке x k+1 приближенное решение может быть вычислено по формуле

Это соотношение и наз. методом Эйлера.

В дальнейшем численные методы были значительно усовершенствованы. Это развитие велось в основном в двух направлениях: методы, получившие в дальнейшем название Рунге-Кутта методов и конечноразностные методы, важнейшим представителем к-рых является Адамса метод.

Предсказывающе-уточняющие методы находят успешное применение при решении жестких систем обыкновенных дифференциальных уравнений. Несмотря на то, что дифференциальные уравнения высокого порядка формально сводятся к системе уравнений 1-го порядка, методы, приспособленные к конкретному виду дифференциального уравнения, иногда оказываются значительно более эффективными. В связи с этим развиваются конечноразностные методы, использующие производные высшего порядка, напр. Штермера метод.

Лит.:[1] Б е р е з и н И. С., Ж и д к о в Н. П., Методы вычислений, 2 изд., т. 2, М., 1962; [2] Бахвалов Н. С., Численные методы, 2 изд., М., 1975; [3] Modern Numerical Methods for ordinary differential equations, Oxf., 1976.

Источник

В чем заключается задача коши

Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах…
Часть II. Глава IV. Обыкновенные дифференциальные уравнения

§ 1. Дифференциальные уравнения первого порядка

1. Основные понятия. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции. Если независимая переменная одна, то уравнение называется обыкновенным; если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.

Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Например:

1) х²у’ + 5xy = у² – обыкновенное дифференциальное уравнение первого порядка;

2) – обыкновенное дифференциальное уравнение второго порядка;

3) y’³ + y»y»’ = х – обыкновенное дифференциальное уравнение третьего порядка;

4) F (х, у, у’, у») = 0 – общий вид обыкновенного дифференциального уравнения второго порядка;

5) – уравнение в частных производных первого порядка.

В этом параграфе рассматриваются обыкновенные дифференциальные уравнения первого порядка, т. е. уравнения вида F (х, у, у’) = 0 или (в разрешенном относительно у’ виде) y’ = f(х, у).

Решением дифференциального уравнения называется такая дифференцируемая функция у = φ (x), которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.

Общим решением дифференциального уравнения первого порядка у’ = f(x, у) в области D называется функция у = φ(x, C), обладающая следующими свойствами: 1) она является решением данного уравнения при любых значениях произвольной постоянной С, принадлежащих некоторому множеству; 2) для любого начального условия у(х0) = у0 такого, что (x0; y0) ∈ 0, существует единственное значение С = С0, при котором решение у = φ(x, C0) удовлетворяет заданному начальному условию.

Всякое решение у = φ(x, C0), получающееся из общего решения у = φ (x, C) при конкретном значении С = С0, называется частным решением.

Задача, в которой требуется найти частное решение уравнения y’ = f(х, у) удовлетворяющее начальному условию у(х0) = y0, называется задачей Коши.

Построенный на плоскости хОу график всякого решения у = φ(х) дифференциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению у = φ(х, С) на плоскости хОу соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной С, а частному решению, удовлетворяющему начальному условию y(x0) = y0, – кривая этого семейства, проходящая через заданную точку М0(x0; у0).

Если функция f(х, у) непрерывна и имеет непрерывную производную в области D, то решение дифференциального уравнения у’= f (х, у) при начальном условии у(х0) = у0 существует и единственно, т. е. через точку (x0; y0) проходит единственная интегральная кривая данного уравнения (теорема Коши).

Особым решением называется такое решение, во всех точках которого условие единственности не выполняется, т. е. в любой окрестности каждой точки (х; у) особого решения существуют по крайней мере две интегральные кривые, проходящие через эту точку.

Особые решения не получаются из общего решения дифференциального управления ни при каких значениях произвольной постоянной С (в том числе и при С = ± ∞).

Особым решением является огибающая семейства интегральных кривых (если она существует), т. е. линия, которая в каждой своей точке касается по меньшей мере одной интегральной кривой.

2. Дифференциальные уравнения с разделяющимися переменными. Дифференциальное уравнение вида

относится к типу уравнений с разделяющимися переменными. Если ни одна из функций f1(x), f2(y), φ1(x), φ2(y) не равна тождественно нулю, то в результате деления исходного уравнения на f2 (x) φ1 (y) оно приводится к виду

Почленное интегрирование последнего уравнения приводит к соотношению

которое и определяет (в неявной форме) решение исходного уравнения. (Решение дифференциального уравнения, выраженное в неявной форме, называют интегралом этого уравнения.)

507. Решить уравнение х(у²-4)dx + y dy = 0.

△ Разделив обе части уравнения на у² – 4 ≠ 0, имеем

Это общее решение данного дифференциального уравнения.

Пусть теперь у² – 4 = 0, т. е. у = ± 2. Непосредственной подстановкой убеждаемся, что у = ±2 – решение исходного уравнения. Но оно не будет особым решением, так как его можно получить из общего решения при С = 0. ▲

508. Найти частный интеграл уравнения у’ cos х = у / ln у, удовлетворяющий начальному условию y(0) = l.

△ Полагая , перепишем данное уравнение в виде

Проинтегрируем обе части уравнения:

, или

Используя начальное условие у = 1 при х = 0, находим С = 0. Окончательно получаем

509. Найти общий интеграл уравнения у’ = tg x tg y.

△ Полагая и разделяя переменные, приходим к уравнению ctg у dy = tg х dx. Интегрируя, имеем

Отсюда находим sin y = C/cos x, или sin y / cos x = С (общий интеграл). ▲

510. Найти частное решение дифференциального уравнения (l + x²)dy + y dx = 0 при начальном условии у(1) = 1.

△ Преобразуем данное уравнение к виду . Интегрируя, получим

, или ln |y| = – arctg x + С

Это и есть общий интеграл данного уравнения.

Теперь, используя начальное условие, найдем произвольную постоянную С; имеем ln 1 = — arctg 1 + С, т. е. С = π/4. Следовательно,

ln у = – arctg х + π/4,

Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах… Ч. II. Стр. 117-119.

Источник

Решение задачи Коши

Содержание:

Задача Коши. Одной из важнейших задач в теории дифференциальных уравнений является так называемая задача Коши. Для уравнения (2),

задача Коши, или начальная задача, ставится следующим образом: среди всех решений уравнения (2) найти такое решение

в котором функция у(х) принимает заданное числовое значение Уо при заданное числовом значении х0 независимой переменной х, т. е.

где и — заданные числа, так что решение (36) удовлетворяет условию:

При этом число называется начальным значением искомой функции, а число — начальным значением независимой переменной. В целом же числа и называются начальными данными решения (36), а условие (38) —начальным условием этого решения.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Задачу Коши геометрически можно сформулировать так: среди всех интегральных кривых уравнения (2)’найти tj (рис. 6), которая проходит через заданную точку

Будем говорить, что задача Коши с начальными условиями (38) имеет единственное решение, если существует та кое число , что в интервале — определено решение такое, что и не существует решения, определенного в этом же интервале и не совпадающего с решением хотя бы в одной точке интервала

отличной от точки В противном случае, т. е. когда задача Коши с начальным условием (38) имеет не одно решение или же совсем не имеет решений, мы будем говорить, что в точке нарушается единственность решения задачи Коши.

Возможно вам будут полезны данные страницы:

Вопрос о единственности решения задачи Коши представляет исключительный интерес как для самой теории дифференциальных уравнений, так и для ее многочисленных приложений, ибо, зная, что решение задачи Коши единственно, мы, найдя решение, удовлетворяющее заданным начальным условиям, уверены, что других решений, удовлетворяющих тем же начальным условиям, нет.

В вопросах естествознания эго приводит к тому, что мы получаем вполне определенный, единственный закон явления, определяемый только дифференциальным уравнением и начальным условием. Иллюстрацией сказанного может служить хотя бы пример 1, рассмотренный во введении.

Заметим, что в простейшем случае задача Коши встречается нам уже в интегральном исчислении, именно там, по существу, доказывается, что если функция f(x) непрерывна в интервале (а, Ь),то единственным решением уравнения

принимающим значение принадлежит интервалу —любое заданное число, является функция*

Эго решение определено ео всем интервале (а, Ь).

Из формулы (40) легко усмотреть характер зависимости решения рассматриваемой задачи Коши как от независимой переменной, так и от начальных данных.

Из формулы (40) видно также, что решение задачи К о ш и дл я простейшего дифференциального уравнения (39) я в-ляется непрерывной и даже непрерывно дифференцируемой функцией начальных данных

Особые случаи задачи Коши. При постановке задачи Коши с начальными данными мы неявно предполагали, что числа х0 и уо конечны и что правая часть уравнения (2) определена и конечна в точке , т. е. уравнение (2) задает в точке определенное направление поля, причем последнее не параллельно оси Оу. Если правая часть уравнения (2) обращается в точке в бесконечность, то следует рассматривать перевернутое уравнение (.

и искать решение (рис. 7), удовлетворяющее начальному условию: . Единственная «особенность» решения этой задачи Коши состоит только в том, что в точке касательная к интегральной кривой параллельна оси Оу.

Совсем другое положение мы будем иметь, если в точке правая часть уравнения (2) по определена. Предположим, что f(x, у) обращается в точке в неопределенность вида Тогда обычная постановка задачи Коши теряет смысл, так как через точку не проходит ни одна интегральная кривая.

В этом случае задача Коши ставится так:

найти решение вида [или обладающее свойством (28) [или (29)], т. е. найти решение, примыкающее к точке

Здесь, так же как и в основном случае задачи Коши, возникают вопросы существования и единственности решения.

Кроме того, здесь возникают и дополнительные вопросы:

1) имеют ли решения, примыкающие к точке , определенную касательную в этой точке? Дело в том, что само уравнение (2) в этом случае не предписывает никакого определенного направления касательной в такой точке ;

2) если интегральные кривые примыкают к точке с определенными направлениями касательной, то каковы эти направления? Сколько кривых входит по данному направлению? В примерах 3 и 4, рассмотренных в п. 4, все интегральные кривые уравнения (30) примыкают к точке (0,0) (где правая часть обращается в о — неопределенность вида ), имея в ней каждая свою касательную, в то время как ни одна из интегральных кривых уравнения (34) не примыкает к точке (0,0), так что для этого уравнения задача Коши с начальными данными не имеет ни одного решения.

В некоторых случаях возникает необходимость искать решения , удовлетворяющие условиям:

Указанные выше особые случаи задачи Коши исследуются в аналитической теории дифференциальных уравнений и в качественной теории дифференциальных уравнений. Во всех случаях задачи Коши наряду с вопросами существования и единственности возникают /вопросы о свойствах решения задачи Коши как функции независимой переменной (аналитический вид, дифференциальные и геометрические свойства и особенности «поведения во всей области существования) и как функции начальных данных. Рассмотрение этих вопросов составляет одну из основных задач теории дифференциальных уравнений.

Достаточное условие существования решения задачи Коши

Предположим, что правая часть уравнения (2) определена и непрерывна в некоторой области G изменения х и у. Тогда, как уже отмечалось раньше (п. 4), уравнение (2) определяет некоторое поле направлений, причем в силу только что сделанного предположения о непрерывности правой части уравнения (2) это ноле направлений непрерывно, так что направления в двух достаточно близких точках разнятся сколь угодно мало. Заметим, что из сделанного предположения о непрерывности

правой части уравнения (2) следует, что всякое решение этого уравнения (если оно существует) будет непрерывно дифференцируемым, так что всякая интегральная кривая будет гладкой. Всякая интегральная кривая, как уже было сказано в п. 4., обладает чем свойством, что в каждой ее точке направление карательной совпадает с направлением поля, определяемым дифференциальным уравнением в этой точке. Попытаемся, пользуясь этим свойством интегральной кривой, найти решение задачи Коши для уравнения (2) с начальными данными из области G.

Возьмем п области G некоторую точку (рис 8) Наклон поля в этой точке равен Проведем через точку -прямую с угловим коэффициентом

На этой прямой возьмем любую точку , принадлежащую области G, и через нее прощую области G, и через нее проведем прямую с угловым коэффициентом, равным наклону поля в этой точке, т. е. На последней прямой возьмем любую точку принадлежащую области G, и проведем через нее прямую с угловым коэффициентом и т. д. Такое же построение можно сделать и влево от точки . Построенная ломаная линия называется ломаной Эйлера.

Можно доказать*, что при сделанном предположении относительно f(x, у) это действительно имеет место, так что для существования непрерывно дифференцируемого решения задачи Коши для уравнения (2) достаточно предположить, что его правая часть непрерывна в окрестности начальных данных (теорема Пеано).

Заметим, однако, что нс исключена возможность существования нескольких последовательностей ломаных Эйлера, проходящих через точку , каждая из которых стремится к своей интегральной кривой, так что в общем случае, нет оснований ожидать, что мы получим единственную интегральную кривую, проходящую через точку . Более того, как показал М. Л. Лаврентьев**, единственность решения может нарушаться даже во всех точках непрерывности правой части уравнения (2).

Таким образом, теорема Пеано есть только теорема существования решения задачи Коши. Единственности решения она не гарантирует.

Достаточные условия существования и единственности решения задачи Коши

Поставим вопрос: каким условиям достаточно подчинить правую часть уравнения (2) в окрестности начальных данных чтобы через точку проходила одна и только одна интегральная кривая этого уравнения» В общем виде этот вопрос мы рассматриваем в гл. V, где пр* некоторых предположениях относительно правой части уравнения (2) мы доказываем существование и единственность решения задачи Коши и показываем, что свойства решения задачи Коши вполне определяются свойствами правой части уравнения (2) и начальными данным и. Сейчас мы приведем без дока-загельства основную теорему существования и единственности (теорему Пикара) для уравнения (2) в упрощенной формулировке.

Теорема. Пусть дано уравнение (2),

и поставлено начальное условие (38),

Предположим, что функция определена в некоторой замкнутой ограниченной области (рис. 9)

с точкой внутри (а и b — заданные положительные числа) и удовлетворяет в ней следующим двум условиям.

У 1. Функция непрерывна и следовательно, ограничена, т. е.

где М—постоянное положительное число, а(х, у) — любая точка области R;

II. Функция f(x, у) имеет ограничейную частную производную по аргументу у, т. е.:

где К — постоянное положительное число, а (х, у)—любая точка области R.

При этих предположениях уравнение (2) имеет единственное решение (36),

удовлетворяющее начальному условию (38). Это решение определено и непрерывно дифференцируемо в некоторой окрестности начального значения х0 независимой переменной х, а именно оно заведомо определено в интервале

где h есть наименьшее из чисел

Из этой теоремы, в частности, следует, что если правая часть уравнения (2) есть полином относительно х и у или любая другая функция, определенная и непрерывная относительно х и у вместе с частной производной по у при всех значениях х и у, то через любую точку проходит одна и только одна интегральная кривая, ибо во всяком прямоугольнике R с центром в точке (х0, уо) оба условия теоремы Пикара будут очевидно выполнены. В этом случае вся плоскость (х, у) будет заполнена не пересекающимися и не касающимися друг друга гладкими интегральными кривыми.

Примеры с решением

Пример 1.

Пусть дано уравнение

и поставлено начальное условие:

Так как правая часть уравнения (45) есть полином относительно х и у, то решение с любыми начальными условиями, в том числе и с начальным условием (46), существует и единственно.

Оценим область определения решения с начальным условием (46).

С этой целью построим прямоугольник R с центром в точке (0, 0),

причем в качестве а и b можно взять любые положительные числа. Будем иметь:

Отсюда видно, что h зависит от выбора чисел а к &*. В частности, при а = b — 1, получим:

Поэтому уравнение (45) имеет единственное решение, заведомо определенное в интервале и удовлетворяющее начальному условию (46). это решение непрерывно дифференцируемо.

С геометрической точки зрения полученный результат означает, что уравнение (45) имеет только одну интегральную кривую, проходящую через начало координат, причем эта интегральная кривая гладкая.

Этот результат приобретает особое значение, если принять во внимание, что уравнение (45) не интегрируется пи в элементарных функциях, пи в квадратурах от элементарных функций, в чем мы убедимся в п. 51. Установленный факт существования и единственноеги решения дает нам основание пытаться искать его другими методами и в том числе находить это решение приближенно.

Пример 2.

Найти решение уравнения

удовлетворяющее начальному условию:

Так как правая часть уравнения (50) вместе с ее частной производной по непрерывна при всех х и у, то через каждую точку плоскости (х, у) проходит единственная интегральная кривая. Это же будет иметь место и в начале координат. Но легко заметить, что у = 0 (ось Ох) есть решение уравнения (50) и это решение проходит через начало координат, так чго оно и будет искомым решением. В силу только что установленной единственности решения уравнение (50) не имеет других решений, проходящих через начало координат.

* Наибольшим значением h будет

Вообще, если в уравнении (2) функция f(x, у) удовлетворяет обоим условиям теоремы Пикара в некоторой окрестности заданной точки (х0, у0) и такова, что , то единственным решением этого уравнения, проходящим через точку , будет прямая

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник