в чем заключается теория пуанкаре
Что доказывает теорема Пуанкаре о возвращении
Все началось еще в конце XIX века, когда ученый из Франции, Анри Пуанкаре, изучал различные части систем, которые могут быть полностью проанализированы. Как обычно, звучит это не так сложно, но именно его труды легли в основу большой задачи и стали одной из загадок, которую ученые современности называют ”Задачами тысячелетия”. Думаю вы легко согласитесь, что если подождать достаточное количество времени, то планеты в небе выстроятся в нужную вам линию. Так же будет и с частицами газа или жидкости, которые могут сколько угодно менять свое положение, но теоретически в один из моментов времени выстроятся относительно друг друга так, как они располагались в момент начала измерений. На словах все просто — рано или поздно это случится, иначе быть не может. Вот только на деле доказать это довольно сложно. Именно над этим и работал Анри Пуанкаре больше века назад. Позже его теории были доказаны, но от этого не стали менее интересными.
Теорий, гипотез, теорем и просто рассуждений очень много. Все их надо доказывать.
Кто такой Анри Пуанкаре
Жюль Анри Пуанкаре (фр. Jules Henri Poincaré) родился 29 апреля 1854 в Нанси, Франция, а умер 17 июля 1912 в Париже, Франция. Он был французским ученым, в сферу интересов которого входили самые разные науки. Среди них были: математика, механика, физика, астрономия и философия.
Кроме того, что он занимался исследованиями, Анри Пуанкаре в разные годы также был главой Парижской академии наук, членом Французской академии и ещё более 30 академий мира, в том числе иностранным членом-корреспондентом Петербургской академии наук.
Физики зафиксировали квантовый шум в лаборатории LIGO – что нужно знать?
Чуть ли не единогласно историки называют Анри Пуанкаре одним из величайших математиков всех времён. Его ставили в один ряд с Гильбертом, последним математиком-универсалом, учёным, способным охватить все математические результаты своего времени.
Анри Пуанкаре сделал для математики настолько много, что некотрые его труды до сих пор приносят нам пользу.
Перу Анри Пуанкаре принадлежат более 500 статей и книг. Все это говорит о нем, как о гении, который даже спустя более 100 лет после своей смерти может изменить мир будущего своими теориями, формулами, рассуждениями и прочими научными трудами.
Что такое теорема возвращения Пуанкаре
Теорема Пуанкаре о возвращении — одна из базовых теорий эргодической теории. Её суть в том, что при сохраняющем меру отображении пространства на себя почти каждая точка вернётся в свою начальную окрестность. На это потребуется огромное, но конечное количество времени.
С одной стороны, все логично, но есть у данной теории и немного непонятное следствие. Например, у нас есть сосуд, который разделен перегородкой на два отсека. В одном находится газ, а во втором ничего. Если убрать перегородку, то газ заполнит собой весь сосуд. Если верить теории повторения, то рано или поздно все частицы газа должны выстроиться в изначальной последовательности в половине сосуда.
Немного развязывает руки то, что время, которое на это потребуется, может быть очень большим. Но такое следствие не совсем корректно, так как изменились условия наблюдения. Зато, если говорить о том, что перегородку мы убирать не будем, объем газа не изменится и ему не придется нарушать законы физики, произвольно меняя свою плотность, и частицы газа рано или поздно действительно займут те места, в которых они были на момент начала наблюдений.
Есть такие загадки науки, которые были понятны гению, но после него никто так и не может этого доказать. Хотя, все понимают, что автор был прав.
Теория Пуанкаре в квантовой системе
Если мы говорим о том, что в традиционной системе повторения возможны и даже неизбежны, то можно предположить, что в квантовой системе, в которой возможны несколько состояний, все немного иначе. Оказывается, это не так, и труды Пуанкаре могут быть применены и к квантовым системам. Однако правила будут немного иными.
Проблема применения заключаются в том, что состояние квантовой системы, которая состоит из большого количества частиц, не может быть измерено с большой точностью, не говоря уже об идеальном измерении. Более того, можно сказать, что частицы в таких системах можно рассматривать в качестве полностью независимых объектов. Учитывая запутанности, не сложно понять, что при анализе таких систем придется столкнуться с большим количеством сложностей.
Несмотря на это, ученые не были бы учеными, если бы не попытались продемонстрировать эффект повторения Пуанкаре в том числе и в квантовых системах. Сделать это у них получилось. Вот только пока это возможно только для систем с очень небольшим числом частиц. Их состояние нужно измерить как можно точнее и обязательно учесть его.
Сказать, что сделать это сложно — ничего не сказать. Главная сложность в том, что время, которое потребуется системе для возвращения в исходное состояние, будет очень сильно возрастать даже при незначительном увеличении количества частиц. Именно поэтому некоторые ученые анализируют не систему в целом, а ее отдельные частицы. Они пытаются понять, возможно ли возвращение к первоначальному значению некоторых участков этой системы.
Для этого они изучают и анализируют поведение ультрахолодного газа. Он состоит из тысяч атомов и удерживается на месте при помощи электромагнитных полей. Описать характеристики подобного квантового газа можно несколькими величинами. Они говорят о том, насколько тесно могут быть связаны частицы с помощью эффектов квантовой механики. В обычной жизни это не так важно и может даже показаться чем-то ненужным, но в квантовой механике это имеет решающее значение.
В итоге, если понять, как такие величины характеризуют систему в целом, можно будет говорить о возможности квантового возвращения. Получив такие знания, можно более смело говорить о том, что мы знаем, что такое газ, какие процессы в нем происходят и даже прогнозировать последствия воздействия на него.
Квантовые системы сильно отличаются от всего, что мы можем себе представить.
В последнее время ученые смогли доказать, что квантовые состояния могут возвращаться, но некоторые поправки в концепцию повторения внести все же стоит. Не стоит пытаться измерить всю квантовую систему в целом, ведь эта задача близка к невозможности. Куда правильнее будет сосредоточиться на некоторых ее элементах, которые можно измерить и предсказать поведение системы в целом.
Если сказать более смело, то такие исследования и наработки в сфере самых разных наук приближают создание настоящего квантового компьютера, а не тех тестовых систем, которые существуют сейчас. Если дело продвинется, то нас ждет большое будущее. А сначала казалось, что это просто измерение чего-то непонятного. Не так ли?
Гипотеза Пуанкаре: история проблемы, доказательство, смысл
По школьному курсу каждый знаком с понятиями теоремы и гипотезы. Как правило, в жизни затрагиваются самые простые и примитивные законы, в то время как математики делают очень сложные предположения и ставят интересные проблемы. Далеко не всегда им самим удается найти решения и доказательства, а в некоторых случаях над этим многие годы бьются их последователи и просто коллеги.
Институт Клея в 2000 году сформировал список из 7 так называемых Проблем Тысячелетия по аналогии с перечнем гипотез, составленным в 1900 году. Те задачи почти все оказались к настоящему времени решены, только одна из них перекочевала в обновленную версию. Сейчас список проблем выглядит следующим образом:
Все они относятся к различным дисциплинам внутри математики и имеют важное значение. Например, уравнения Навье-Стокса относятся к гидродинамике, а на практике могут описать поведение вещества в земной магме или пригодиться в предсказании погоды. Но все эти проблемы все еще ищут своего доказательства или опровержения. Кроме одной.
Теорема Пуанкаре
Объяснить простыми словами, в чем заключается эта проблема, довольно непросто, но попробовать можно. Представим себе сферу, к примеру, мыльный пузырь. Все точки его поверхности равноудалены от его центра, который ей не принадлежит. Но это двумерное тело, а гипотеза говорит о трехмерном. Это представить уже невозможно, но на то у нас и есть теоретическая математика. При этом, разумеется, все точки этого тела также будут удалены от центра.
История
Французский математик Анри Пуанкаре занимался самыми разными областями науки. О его достижениях может сказать, к примеру, тот факт, что совершенно независимо от Альберта Эйнштейна он выдвинул основные положения специальной теории относительности. В 1904 году он поднял проблему доказательства того, что любое трехмерное тело, обладающее некоторыми свойствами сферы, ею и является с точностью до деформации. Позднее она была расширена и обобщена, и стала частным случаем гипотезы Терстона, сформулированной в 1982 году.
Формулировка
Пуанкаре изначально оставил такое утверждение: всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере. В дальнейшем оно было расширено и обобщено. И все же на протяжении длительного времени именно изначальная задача вызывала больше всего проблем, и была решена лишь через 100 лет после ее появления.
Интерпретация и смысл
О том, что такое гомеоморфность, речь уже шла. Теперь стоит поговорить о компактности и односвязности. Первое означает лишь, что многообразие имеет ограниченные размеры, не может быть непрерывно и бесконечно растянуто.
Доказательство
Не стоит думать, что из десятков математиков, работавших по всему миру, никто не продвинулся ни на йоту, занимаясь этой проблемой. Наоборот, прогресс был, и в конце концов он привел к результату. Сам Пуанкаре не успел закончить работу, но его исследования серьезно продвинули всю топологию.
В 1982 году и для 4 было найдено доказательство, оставалось только 3. В том же году Терстон сформулирован гипотезу о геометризации, при этом теория Пуанкаре стала ее частным случаем.
На 20 лет гипотеза Пуанкаре была как будто забыта. В 2002 году российский математик Григорий Перельман представил решение в общих чертах, спустя полгода сделав некоторые дополнения. Уже позже это доказательство проверяли и доводили «до блеска» американские и китайские ученые. А сам Перельман словно потерял к проблеме весь интерес, хотя он решил более общую задачу о геометризации, для которой гипотеза Пуанкаре является лишь частным случаем.
Признание и оценки
Разумеется, это сразу стало сенсацией, ведь решение одной из Проблем Тысячелетия просто не могло оказаться незамеченным. Еще больше удивления вызывал тот факт, что Григорий Перельман отказался от всех наград и премий, сообщив, что ему и так прекрасно живется. В умах обывателей он сразу стал примером того самого полусумасшедшего гения, которого интересует только наука.
Все это вызвало много обсуждений в прессе и СМИ, что популярность математика стала его тяготить. Летом 2014 года прошла информация о том, что Перельман уехал работать в Швецию, но это оказалось лишь слухами, он все еще скромно живет в Санкт-Петербурге и почти ни с кем не общается. Среди наград, присужденных ему, были не только премия института Клея, но и престижная медаль Филдса, но он отказался от всего. Впрочем, Гамильтон, который по оценкам Перельмана сделал не меньший вклад в доказательство, тоже не был забыт. В 2009 и 2011 годах он также удостоился некоторых престижных наград и премий.
Отражение в культуре
Несмотря на то что для простых обывателей как постановка, так и решение этой проблемы представляют мало смысла, о доказательстве стало известно довольно быстро. В 2008 году по этому поводу японским режиссером Масахито Касуга был снят документальный фильм «Чары гипотезы Пуанкаре», посвященный столетним попыткам решить эту задачу.
Теорема Пуанкаре простыми словами (6 фото)
Доказательство этой гипотезы российским математиком Григорием Перельманом привело к некоторым очень интересным выводам с точки зрения нашего понимания мира.
Жюль Анри Пуанкаре (1854-1912) возглавлял Парижскую академию наук и был избран в научные академии 30 стран мира. Он имел масштаб Леонардо: его интересы охватывали физику, механику, астрономию, философию. Математики же всего мира до сих пор говорят, что только два человека в истории по-настоящему знали эту науку: немец Давид Гилберт (1862-1943) и Пуанкаре.
В 1904 году учёный опубликовал работу, содержавшую среди прочего предположение, получившее название теорема Пуанкаре. Поиск доказательства истинности этого утверждения занял около века.
Основатель топологии
Математический гений Пуанкаре впечатляет количеством разделов науки, где им были разработаны теоретические основы различных процессов и явлений. Во времена, когда ученые совершали прорывы в новые миры космоса и в глубины атома, было не обойтись без единой основы общей теории мироздания. Такой базой стали ранее неизвестные отрасли математики.
Пуанкаре искал новый взгляд на небесную механику, он создал качественную теорию дифференциальных уравнений, теорию автоморфных функций. Исследования ученого стали основой специальной теории относительности Эйнштейна. Теорема Пуанкаре о возвращении говорила среди прочего о том, что понять свойства глобальных объектов или явлений можно исследуя составляющие их частицы и элементы. Это дало мощный толчок научным поискам в физике, химии, астрономии и т.д.
Развитием неэвклидовой геометрии стало возникновение топологии – отрасли математики, которую называли геометрией размещения. Она изучает пространственные взаимоотношения точек, линий, плоскостей, тел и т.д. без учета их метрических свойств. Теорема Пуанкаре, ставшая символом самых трудноразрешимых задач в науке, возникла именно в недрах топологии.
Одна из семи задач тысячелетия
• Равенство классов P и NP (о соответствии алгоритмов решения задачи и методов проверки их правильности).
• Гипотеза Ходжа (о связи объектов и их подобия, составленного для их изучения из «кирпичиков» с определенными свойствами).
• Гипотеза Пуанкаре (всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере).
• Гипотеза Римана (о закономерности размещения простых чисел).
• Теория Янга — Миллса (уравнения из области элементарных частиц, описывающие различные виды взаимодействий).
• Существование и гладкость решений уравнений Навье — Стокса (описывают турбулентность течений воздуха и жидкостей).
• Гипотеза Бёрча — Свиннертон-Дайера (об уравнениях, описывающих эллиптические кривые).
Каждая эта проблема имела очень долгую историю, поиски их решения приводили к возникновению целых новых научных направлений, но единственно правильные ответы на поставленные вопросы не находились. Понимающие люди говорили, что деньги фонда Клэя в безопасности, но так было лишь до 2002 года – появился тот, кто доказал теорему Пуанкаре. Правда, деньги он не взял.
Классическая формулировка
Гипотеза, для которой найдено подтверждение, становится теоремой, имеющей корректное доказательство. Именно это произошло с высказанным Пуанкаре предположением о свойствах трехмерных сфер. В более общем виде этот постулат говорил о гомеоморфности всякого многообразия размерности n и сферы размерности n как необходимом условии их гомотопической эквивалентности. Знаменитая теперь теорема Пуанкаре относится к варианту, когда n=3. Именно в трехмерном пространстве математиков ждали затруднения, для других случаев доказательства были найдены быстрее.
Чтобы хоть немного постичь смысл теоремы Пуанкаре, не обойтись без знакомства с основными понятиями топологии.
Гомеоморфизм
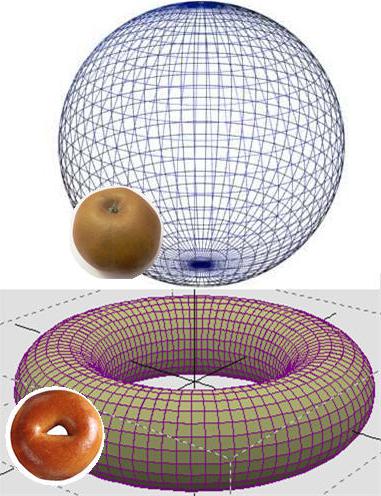
Топология, говоря о гомеоморфизме, определяет его как взаимно-однозначное соответствие между точками одной и другой фигуры, в некотором смысле неотличимость. Неподготовленному сложно даётся теорема Пуанкаре. Для чайников можно привести самый популярный пример гомеоморфных фигур – шар и куб, также гомеоморфны бублик и кружка, но не кружка и куб. Фигуры гомеоморфны, если одну фигуру можно получить произвольной деформацией из другой, причем это преобразование ограничено некоторыми свойствами поверхности фигуры: её нельзя рвать, прокалывать, разрезать.
Если куб раздуть, он легко может стать шаром, если шар примять встречными движениями, можно получить кубик. Наличие дырки у бублика и дырки, образованной ручкой у кружки, делает их гомеоморфными, та же дырка делает невозможным превращение кружки в шар или куб.
Связность
Дырка – важное понятие, определяющее свойства объекта, но категория совершенно не математическая. Было введено понятие связности. Его содержат многие топологические постулаты, в том числе и теорема Пуанкаре. Простыми словами можно говорить так: если поверхность шара обернуть петлей из резиновой ленты, она, сжимаясь, соскользнёт. Этого не произойдет, если имеется отверстие, как у тора-бублика, сквозь которое можно продеть эту ленту. Таким образом определяется главный признак сходства или отличия объектов.
Многообразие
Самая адекватная аналогия этих категорий – поверхность земли. Изображение её поверхности представляет собой карты отдельных её районов, собранные в атлас. На глобусе эти изображения обретают форму шара, который относительно пространства Вселенной превращается в точку.
Трехмерная сфера
Математики приводят ещё и такое описание трехмерной сферы: допустим, что к нашему привычному пространству, считаемому неограниченным и определяемому тремя координатами (X, Y, Z), добавлена точка (на бесконечности) таким образом, что в неё всегда можно попасть, двигаясь в любом направлении по прямой линии, т.е. любая прямая в этом пространстве становится окружностью. Говорят, что есть люди, которые могут это вообразить и спокойно ориентироваться в таком мире.
Для них обычное дело – трехмерный тор. Такой объект можно получить путем дважды повторенного совмещения в одну точку двух, расположенных на противоположных (например, правой и левой, верхней и нижней) гранях куба. Чтобы попытаться представить трехмерный тор с привычных нам позиций, следует провести абсолютно нереальный эксперимент: необходимо выбрать направления, взаимно перпендикулярные, – вверх, влево и вперед – и начать двигаться в любом из них по прямой. Через какое-то (конечное) время с противоположного направления мы вернемся в исходную точку.
Такое геометрическое тело имеет принципиальное значение, если хотеть понять, что такое теорема Пуанкаре. Доказательство Перельмана сводится к обоснованию существования в трехмерном пространстве лишь одного односвязного компактного многообразия – 3-сферы, другие, как 3-тор, неодносвязные.
Долгий путь к истине
Прошло более полувека, прежде чем появилось решение теоремы Пуанкаре для больших чем 3 размерностей. Стивен Смэйл (род. 1930), Джон Роберт Стэллингс (1935-2008), Эрик Кристофер Зиман (род. 1925) нашли решение для n, равного 5, 6 и равного или больше 7. Только в 1982 году Майкл Фридман (род. 1951) был удостоен высшей математической награды – Филдсовской премии – за доказательство теоремы Пуанкаре для более сложного случая: когда n=4.
Обыкновенный гений
Многие специалисты, особенно российские, отмечают что Григорий Яковлевич был подготовлен к невиданному взлету высоким классом ленинградской школы геометров, какую он прошел на мехмате Ленинградского госуниверситета и в аспирантуре при Математическом институте им. В.А. Стеклова. Став кандидатом наук, он стал работать в нем.
Трудное время 90-х заставило молодого ученого уехать на работу в США. Те, кто знал его тогда, отмечали его аскетизм в быту, увлечённость работой, прекрасную подготовку и высокую эрудицию, которые и стали залогом того, что Перельман доказал теорему Пуанкаре. Вплотную он занялся этой проблемой после возвращения в Санкт-Петербург в 1996 году, но начал думать над ней еще в США.
Верное направление
Григорий Яковлевич отмечает, что его всегда увлекали сложные проблемы, такие как теорема Пуанкаре. Доказательство Перельман стал искать в направлении, вынесенном из беседы с профессором Колумбийского университета Ричардом Гамильтоном (род. 1943). Во время пребывания в США он специально ездил из другого города на лекции этого неординарного ученого. Перельман отмечает прекрасное доброжелательное отношение профессора к молодому математику из России. В их разговоре Гамильтон упомянул о потоках Риччи – системе дифференциальных уравнений – как способе решения теорем геометризации.
Впоследствии Перельман пытался связаться с Гамильтоном и обсудить ход работы над задачей, но не получил ответа. Долгое время после возвращения на родину Григорий Яковлевич провел наедине с труднейшей задачей, которой была теорема Пуанкаре. Доказательство Перельмана – итог огромных усилий и самоотречения.
Гамильтон пришел в тупик, когда увидел, что при преобразованиях кривых под действием потоков Риччи образуются сингулярные (обращающиеся в бесконечность) зоны, которые не предусматривала теорема Пуанкаре. Простыми словами, Перельману удалось нейтрализовать образование таких зон, и многообразие благополучно превратилось в сферу.
Потоки Риччи
Односвязное 3-мерное многообразие наделяется геометрией, вводятся метрические элементы с расстоянием и углами. Легче понять это на одномерных многообразиях. Гладкая замкнутая кривая на эвклидовой плоскости наделяется в каждой точке касательным вектором единичной длины. При обходе кривой вектор поворачивается с определенной угловой скоростью, которая определяет кривизну. Где линия изогнута сильнее, кривизна больше. Кривизна положительна, если вектор скорости повернут в сторону внутренней части плоскости, которую делит наша линия, и отрицательна, если повернут вовне. В местах перегиба кривизна равна 0.
Нет пророка…
Он взошел на свой Эверест, каким признается математиками теорема Пуанкаре. Доказательство Перельман выложил в Интернет в виде трех небольших статей. Они немедленно вызвали ажиотаж, хотя русский математик не пошел положенной дорогой – публикация в специализированном журнале в сопровождении профессиональных рецензий. Григорий Яковлевич в течение месяца разъяснял в университетах США суть своего открытия, но число до конца понявших ход его мысли увеличивалось очень медленно.
Лишь через четыре года появилось заключение самых больших авторитетов: доказательства русского математика корректны, первая из проблем тысячелетия решена.
Эпоха соцсетей
Ему пришлось пережить ажиотаж и хамство в соцсетях, молчание тех, кого он уважал, и крики других, учивших его жизни. Энергичные китайцы сначала оценили его вклад в решение проблемы в 25 %, себе и другим насчитав 80! Потом вроде бы пришло мировое признание, но выдержать такое дано не каждому.
Гипотеза Пуанкаре
Гипотеза Пуанкаре — это доказанная гипотеза о том, что если трёхмерная поверхность чем-то похожа на сферу, и если её расправить, она превратится именно в сферу.
Одна из версий официальной формулировки гипотезы Пуанкаре́ звучит так: «Всякое связное, односвязное, компактное трёхмерное многообразие без края гомеоморфно сфере S³».
Гипотеза Пуанкаре была сформулирована в 1904 году известным французским математиком Анри Пуанкаре. В 2002–2003 годах она была доказана русским математиком Григорием Перельманом. После этого Гипотеза Пуанкаре стала именоваться теоремой Пуанкаре — Перельман.
Топология — простыми словами это «геометрия резинового листа» или «резиновая геометрия» т.к. объекты растягиваются и сжимаются как резина и их невозможно сломать; топология изучает свойства пространств, которые неизменны под давлением любой непрерывной деформации. Гипотеза Пуанкаре связана с топологией.
Доказательство
Простыми словами: Перельман доказал при помощи потока Риччи, что при эволюции любая замкнутая кривая на плоскости ведёт себя одинаково и превращается в окружность.
В своих статьях, где Перельман опубликовал идеи доказательства, он также доказал гипотезу о геометризации Уильяма Тёрстона, частным случаем которой является гипотеза Пуанкаре.
Гипотеза геометризации Уильяма Тёрстона гласит, что каждое трёхмерное многообразие локально изометрично только одному из восьми различных типов (изометрично — в науке это то, что относится к равенству меры или этим характеризуется).
Доказательство Перельмана было основано на теории потока Риччи и использовало результаты Чигера, Громова и самого Перельмана о метрических пространствах.
Метрическое пространство — это набор, где есть функция измерения расстояния между точками и который называется метрикой.
Что доказательство гипотезы дало науке?
В плане астрономии эта теорема предполагает, что если наша Вселенная имеет характеристики односвязного компактного многообразия без края, следовательно, она является трёхмерной сферой. Однако ранее считалось, что Вселенная является бесконечной (т.е. имеет форму евклидового трёхмерного пространства).
Теорема Перельмана — Пуанкаре также имеет огромное значение для математики, особенно способ её доказательства. Эта теорема считается математической формулой Вселенной. Она описывает наш мир, который является гладким трёхмерным многообразием.