в чем заключается теорема пуанкаре
О гипотезе Пуанкаре. Лекция в Яндексе
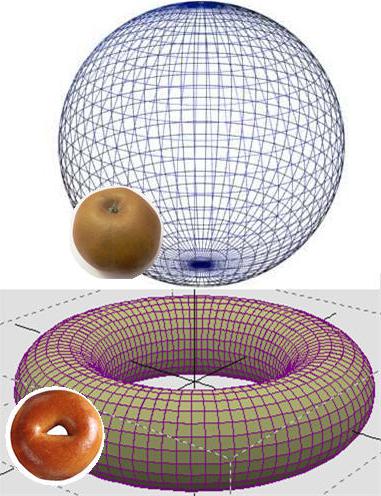
Еще в XIX веке было известно, что если любую замкнутую петлю, лежащую на двумерной поверхности, можно стянуть в одну точку, то такую поверхность легко превратить в сферу. Так, поверхность воздушного шарика удастся трансформировать в сферу, а поверхность бублика – нет (легко вообразить себе петлю, которая в случае с бубликом не стянется в одну точку). Гипотеза, высказанная французским математиком Анри Пуанкаре в 1904 году, гласит, что аналогичное утверждение верно и для трехмерных многообразий.
Доказать гипотезу Пуанкаре удалось только в 2003 году. Доказательство принадлежит нашему соотечественнику Григорию Перельману. Эта лекция проливает свет на объекты, необходимые для формулировки гипотезы, историю поиска доказательства и его основные идеи.
Читают лекцию доценты механико-математического факультета МГУ к. ф-м. н. Александр Жеглов и к. ф.-м. н. Федор Попеленский.
Если не вдаваться в математические подробности, то вопрос, поднимаемый гипотезой Пуанкаре можно следующим образом: как охарактеризовать (трехмерную) сферу? Чтобы правильно понять этот вопрос, нужно познакомиться с одним из важнейших понятий в топологии – гомеоморфизмом. Разобравшись с ним, мы сможем точно сформулировать гипотезу Пуанкаре.
Чтобы совсем уж не залезать в математические подробности формального определения, мы скажем, что две фигуры считаются гомеоморфными, если можно установить такое взаимно-однозначно соответствие между точками этих фигур, при котором близким точкам одной фигуры соответствуют близкие точки другой фигуры и наоборот. Пропущенные нами подробности состоят как раз в адекватной формализации близости точек.
Легко понять, что две фигуры гомеоморфны, если одну из другой можно получить произвольной деформацией, при которой запрещено «портить» поверхности (рвать, сминать области в точку, делать дырки и т.п.).
Например, чтобы получить из диска полусферу, как показано на картинке выше, нам потребуется просто нажать сверху в его центр, придерживая внешний обод. Можно представлять себе, что поверхности сделаны из идеальной резины, так что все фигуры могут сжиматься и растягиваться как угодно. Нельзя делать только две вещи: разрывать и склеивать.
Более точное (но все же не окончательное с точки зрения строгости) представление о гомеоморфных фигурах мы будем иметь, если разрешим еще одну операцию: можно сделать на фигуре разрез, перекрутить, завязать, развязать и т.п., но потом обязательно заклеить разрез как было.
Приведем еще один пример. Представим себе яблоко, в котором червяк прогрыз ход в виде узла и небольшую пещеру.
С точки зрения топологии поверхность этого яблока все равно останется сферой, т.к. если стянуть все это определенным образом, мы получим поверхность яблока в том же виде, как было до того, как червяк начал его есть.
Для закрепления попробуйте классифицировать буквы латинского алфавита с точностью до гомеоморфизма (т.е. выясните, какие буквы гомеоморфны, а какие — нет). Ответ зависит начертания букв (от типа шрифта или от гарнитуры), и для простейшего варианта начертания он приведен на следующем рисунке:
Из 26 букв у нас получается всего 8 классов.
На следующей картинке изображены гиря, кофейная чашка, бублик, сушка и кренделек. С топологической точки зрения поверхности гири, кофейной чашки, бублика и сушки одинаковы, т.е. гомеоморфны. Что касается кренделька, то он приведен здесь для сравнения с поверхностью, которую в топологии часто называют кренделем (он изображен в правом нижнем углу рисунка). Как вы, наверное, уже понимаете, и топологический крендель, и съедобный крендель отличаются от тора.
Формальная постановка вопроса
Пусть M – замкнутое связное многообразие размерности 3. Пусть на нем любая петля может быть стянута в точку. Тогда M гомеоморфно трехмерной сфере.
Наибольшую трудность для неподготовленного человека здесь вызывает понятие «многообразия размерности 3» и свойства, выраженные словами «замкнутое» и «связное». Поэтому мы попробуем разобраться со всеми этими понятиями и свойствами на примере размерности 2, в этом случаем многое кардинально упрощается.
Гипотеза Пуанкаре для поверхностей
Пусть M – замкнутая связная поверхность (многообразие размерности 2). Пусть на ней любая петля может быть стянута в точку. Тогда поверхность M гомеоморфна двумерной сфере.
Сначала определим, что такое поверхность. Возьмем конечный набор многоугольников, разбиваем все их стороны (ребра) на пары (т.е. всего сторон у всех многоугольников должно быть четное число), в каждой паре выбираем, каким из двух возможных способов будем их склеивать. Склеиваем. В результате поучается замкнутая поверхность.
Если полученная поверхность состоит из одного куска, а не из нескольких отдельных, то говорят, что поверхность связна. С формальной точки зрения это значит, что после склейки из любой вершины любого многоугольника можно по ребрам пройти в любую другую вершину.
Вот простой пример: если считать, что на картинке выше все треугольники правильные, то после склеивания у нас должен получиться правильный тетраэдр, поверхность которого также гомеоморфна сфере.
Формально нужно требовать, чтобы из любой вершины любого многоугольника после склейки можно было пройти в любую вершину любого многоугольника (по ребрам).
Нетрудно сообразить, что связную поверхность можно склеить и из одного многоугольника. На рисунке видна идея, как это обосновывается:
Рассмотрим примеры простейших склеек:
В первом случае у нас получится сфера:
Во втором случае у нас получится тор (поверхность бублика, мы встречались с ним раньше):
В третьем случае получится так называемая бутылка Клейна:
Если склеивать не все стороны многоугольника, то получится поверхность с краем:
Важно отметить, что после склейки «шрамы» от нее носят чисто «косметический характер. Все точки поверхности равноправны: у любой точки имеется окрестность гомеоморфная диску.
Две поверхности считаются гомеоморфными, если схемы склейки каждой из них можно так разрезать на схемы склейки из более мелких многоугольников, что схемы склейки станут одинаковыми.
Разберем это утверждение на примере разбиения поверхности куба на части, из которых можно сложить развертку тетраэдра:
Верен и более общий факт: поверхности всех выпуклых многогранников – это сферы.
Теперь подробнее остановимся на понятии петли. Петял — это замкнутая кривая на рассматриваемой поверхности. Две петли называются гомотопными, если одну из них можно продеформировать в другую без разрывов и склеек, оставаясь на поверхности. Ниже приведен простейший случай стягивания петли на плоскости или сфере:
Даже если петля на плоскости или сфере имеет самопересечения, ее все равно можно стянуть:
На плоскости можно стянуть любую петлю:
А вот какие петли бывают на торе:
Стянуть такие петли невозможно. (К сожалению, доказательство выходит довольно далеко за рамки нашего рассказа.) Более того, показанные петли на торе не гомотопны. Предлагаем слушателям или читателям найти еще одну петлю на торе, не гомотопную этим двум — это очень простой вопрос. После этого попробуйте найти на торе четвертую петлю, не гомотопную этим трем — это будет несколько сложнее.
Эйлерова характеристика
Теперь, когда мы познакомились со всеми основными понятиями из формулировки гипотезы Пуанкаре, попробуем приступить к доказательству двумерного случая (лишний раз отметим, что это многократно проще трехмерного случая). А поможет нам в этом эйлерова характеристика.
Эйлеровой характеристикой поверхности M назовем число B−P+Г. Здесь Г — число многоугольников, Р — это число ребер после склейки (в случае рассматриваемых поверхностей это половина числа сторон всех многоугольников), B — это число вершин, которое получается после склейки после склейки.
Если две схемы склейки задают гомеоморфные поверхности, то у этих схем числа B−P+Г одинаковы, т. е. B−P+Г является инвариантом поверхности.
Если поверхность уже как-то задана, то надо нарисовать на ней какой-нибудь граф, чтобы после разрезания по нему поверхность распалась на куски гомеоморфные дискам (например, кольца запрещены). Затем подсчитываем величину B−P+Г — это и есть эйлерова характеристика поверхности.
Будут ли гомеоморфны поверхности с одинаковыми эйлеровыми характеристиками, мы узнаем позже. Но совершенно точно можно утверждать, что если эйлеровы характеристики у поверхностей разные, то поверхности не гомеоморфны.
Знаменитое соотношение B−P+Г=2 для выпуклых многоугольников (теорема Эйлера) является частным случаем этой теоремы. В данном случае речь идет о конкретной поверхности — о сфере. Замечание Обозначение: Эйлерову характеристику поверхности M будем обозначать через χ(M): χ(M) = B − P + Γ
Если поверхность M связна, то χ(M) ≤ 2, причем χ(M) = 2 тогда и только тогда, когда M гомеоморфна сфере.
Посмотрев лекцию до конца, вы узнаете, как же все-таки доказывается гипотеза Пуанкаре в размерности 2, и как Григорию Перельману удалось доказать ее в размерности 3.
Теорема Пуанкаре простыми словами
Жюль Анри Пуанкаре (1854-1912) возглавлял Парижскую академию наук и был избран в научные академии 30 стран мира. Он имел масштаб Леонардо: его интересы охватывали физику, механику, астрономию, философию. Математики же всего мира до сих пор говорят, что только два человека в истории по-настоящему знали эту науку: немец Давид Гилберт (1862-1943) и Пуанкаре.
В 1904 году учёный опубликовал работу, содержавшую среди прочего предположение, получившее название теорема Пуанкаре. Поиск доказательства истинности этого утверждения занял около века.
Основатель топологии
Математический гений Пуанкаре впечатляет количеством разделов науки, где им были разработаны теоретические основы различных процессов и явлений. Во времена, когда ученые совершали прорывы в новые миры космоса и в глубины атома, было не обойтись без единой основы общей теории мироздания. Такой базой стали ранее неизвестные отрасли математики.
Пуанкаре искал новый взгляд на небесную механику, он создал качественную теорию дифференциальных уравнений, теорию автоморфных функций. Исследования ученого стали основой специальной теории относительности Эйнштейна. Теорема Пуанкаре о возвращении говорила среди прочего о том, что понять свойства глобальных объектов или явлений можно исследуя составляющие их частицы и элементы. Это дало мощный толчок научным поискам в физике, химии, астрономии и т.д.
Развитием неэвклидовой геометрии стало возникновение топологии – отрасли математики, которую называли геометрией размещения. Она изучает пространственные взаимоотношения точек, линий, плоскостей, тел и т.д. без учета их метрических свойств. Теорема Пуанкаре, ставшая символом самых трудноразрешимых задач в науке, возникла именно в недрах топологии.
Одна из семи задач тысячелетия
• Равенство классов P и NP (о соответствии алгоритмов решения задачи и методов проверки их правильности).
• Гипотеза Ходжа (о связи объектов и их подобия, составленного для их изучения из «кирпичиков» с определенными свойствами).
• Гипотеза Пуанкаре (всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере).
• Гипотеза Римана (о закономерности размещения простых чисел).
• Теория Янга — Миллса (уравнения из области элементарных частиц, описывающие различные виды взаимодействий).
• Существование и гладкость решений уравнений Навье — Стокса (описывают турбулентность течений воздуха и жидкостей).
• Гипотеза Бёрча — Свиннертон-Дайера (об уравнениях, описывающих эллиптические кривые).
Каждая эта проблема имела очень долгую историю, поиски их решения приводили к возникновению целых новых научных направлений, но единственно правильные ответы на поставленные вопросы не находились. Понимающие люди говорили, что деньги фонда Клэя в безопасности, но так было лишь до 2002 года – появился тот, кто доказал теорему Пуанкаре. Правда, деньги он не взял.
Классическая формулировка
Гипотеза, для которой найдено подтверждение, становится теоремой, имеющей корректное доказательство. Именно это произошло с высказанным Пуанкаре предположением о свойствах трехмерных сфер. В более общем виде этот постулат говорил о гомеоморфности всякого многообразия размерности n и сферы размерности n как необходимом условии их гомотопической эквивалентности. Знаменитая теперь теорема Пуанкаре относится к варианту, когда n=3. Именно в трехмерном пространстве математиков ждали затруднения, для других случаев доказательства были найдены быстрее.
Чтобы хоть немного постичь смысл теоремы Пуанкаре, не обойтись без знакомства с основными понятиями топологии.
Гомеоморфизм
Топология, говоря о гомеоморфизме, определяет его как взаимно-однозначное соответствие между точками одной и другой фигуры, в некотором смысле неотличимость. Неподготовленному сложно даётся теорема Пуанкаре. Для чайников можно привести самый популярный пример гомеоморфных фигур – шар и куб, также гомеоморфны бублик и кружка, но не кружка и куб. Фигуры гомеоморфны, если одну фигуру можно получить произвольной деформацией из другой, причем это преобразование ограничено некоторыми свойствами поверхности фигуры: её нельзя рвать, прокалывать, разрезать.
Если куб раздуть, он легко может стать шаром, если шар примять встречными движениями, можно получить кубик. Наличие дырки у бублика и дырки, образованной ручкой у кружки, делает их гомеоморфными, та же дырка делает невозможным превращение кружки в шар или куб.
Связность
Дырка – важное понятие, определяющее свойства объекта, но категория совершенно не математическая. Было введено понятие связности. Его содержат многие топологические постулаты, в том числе и теорема Пуанкаре. Простыми словами можно говорить так: если поверхность шара обернуть петлей из резиновой ленты, она, сжимаясь, соскользнёт. Этого не произойдет, если имеется отверстие, как у тора-бублика, сквозь которое можно продеть эту ленту. Таким образом определяется главный признак сходства или отличия объектов.
Многообразие
Самая адекватная аналогия этих категорий – поверхность земли. Изображение её поверхности представляет собой карты отдельных её районов, собранные в атлас. На глобусе эти изображения обретают форму шара, который относительно пространства Вселенной превращается в точку.
Трехмерная сфера
Математики приводят ещё и такое описание трехмерной сферы: допустим, что к нашему привычному пространству, считаемому неограниченным и определяемому тремя координатами (X, Y, Z), добавлена точка (на бесконечности) таким образом, что в неё всегда можно попасть, двигаясь в любом направлении по прямой линии, т.е. любая прямая в этом пространстве становится окружностью. Говорят, что есть люди, которые могут это вообразить и спокойно ориентироваться в таком мире.
Для них обычное дело – трехмерный тор. Такой объект можно получить путем дважды повторенного совмещения в одну точку двух, расположенных на противоположных (например, правой и левой, верхней и нижней) гранях куба. Чтобы попытаться представить трехмерный тор с привычных нам позиций, следует провести абсолютно нереальный эксперимент: необходимо выбрать направления, взаимно перпендикулярные, – вверх, влево и вперед – и начать двигаться в любом из них по прямой. Через какое-то (конечное) время с противоположного направления мы вернемся в исходную точку.
Такое геометрическое тело имеет принципиальное значение, если хотеть понять, что такое теорема Пуанкаре. Доказательство Перельмана сводится к обоснованию существования в трехмерном пространстве лишь одного односвязного компактного многообразия – 3-сферы, другие, как 3-тор, неодносвязные.
Долгий путь к истине
Прошло более полувека, прежде чем появилось решение теоремы Пуанкаре для больших чем 3 размерностей. Стивен Смэйл (род. 1930), Джон Роберт Стэллингс (1935-2008), Эрик Кристофер Зиман (род. 1925) нашли решение для n, равного 5, 6 и равного или больше 7. Только в 1982 году Майкл Фридман (род. 1951) был удостоен высшей математической награды – Филдсовской премии – за доказательство теоремы Пуанкаре для более сложного случая: когда n=4.
Обыкновенный гений
Многие специалисты, особенно российские, отмечают что Григорий Яковлевич был подготовлен к невиданному взлету высоким классом ленинградской школы геометров, какую он прошел на мехмате Ленинградского госуниверситета и в аспирантуре при Математическом институте им. В.А. Стеклова. Став кандидатом наук, он стал работать в нем.
Верное направление
Григорий Яковлевич отмечает, что его всегда увлекали сложные проблемы, такие как теорема Пуанкаре. Доказательство Перельман стал искать в направлении, вынесенном из беседы с профессором Колумбийского университета Ричардом Гамильтоном (род. 1943). Во время пребывания в США он специально ездил из другого города на лекции этого неординарного ученого. Перельман отмечает прекрасное доброжелательное отношение профессора к молодому математику из России. В их разговоре Гамильтон упомянул о потоках Риччи – системе дифференциальных уравнений – как способе решения теорем геометризации.
Гамильтон пришел в тупик, когда увидел, что при преобразованиях кривых под действием потоков Риччи образуются сингулярные (обращающиеся в бесконечность) зоны, которые не предусматривала теорема Пуанкаре. Простыми словами, Перельману удалось нейтрализовать образование таких зон, и многообразие благополучно превратилось в сферу.
Потоки Риччи
Односвязное 3-мерное многообразие наделяется геометрией, вводятся метрические элементы с расстоянием и углами. Легче понять это на одномерных многообразиях. Гладкая замкнутая кривая на эвклидовой плоскости наделяется в каждой точке касательным вектором единичной длины. При обходе кривой вектор поворачивается с определенной угловой скоростью, которая определяет кривизну. Где линия изогнута сильнее, кривизна больше. Кривизна положительна, если вектор скорости повернут в сторону внутренней части плоскости, которую делит наша линия, и отрицательна, если повернут вовне. В местах перегиба кривизна равна 0.
Нет пророка…
Он взошел на свой Эверест, каким признается математиками теорема Пуанкаре. Доказательство Перельман выложил в Интернет в виде трех небольших статей. Они немедленно вызвали ажиотаж, хотя русский математик не пошел положенной дорогой – публикация в специализированном журнале в сопровождении профессиональных рецензий. Григорий Яковлевич в течение месяца разъяснял в университетах США суть своего открытия, но число до конца понявших ход его мысли увеличивалось очень медленно.
Лишь через четыре года появилось заключение самых больших авторитетов: доказательства русского математика корректны, первая из проблем тысячелетия решена.
Эпоха соцсетей
Ему пришлось пережить ажиотаж и хамство в соцсетях, молчание тех, кого он уважал, и крики других, учивших его жизни. Энергичные китайцы сначала оценили его вклад в решение проблемы в 25 %, себе и другим насчитав 80! Потом вроде бы пришло мировое признание, но выдержать такое дано не каждому.
Гипотеза Пуанкаре: история проблемы, доказательство, смысл
По школьному курсу каждый знаком с понятиями теоремы и гипотезы. Как правило, в жизни затрагиваются самые простые и примитивные законы, в то время как математики делают очень сложные предположения и ставят интересные проблемы. Далеко не всегда им самим удается найти решения и доказательства, а в некоторых случаях над этим многие годы бьются их последователи и просто коллеги.
Институт Клея в 2000 году сформировал список из 7 так называемых Проблем Тысячелетия по аналогии с перечнем гипотез, составленным в 1900 году. Те задачи почти все оказались к настоящему времени решены, только одна из них перекочевала в обновленную версию. Сейчас список проблем выглядит следующим образом:
Все они относятся к различным дисциплинам внутри математики и имеют важное значение. Например, уравнения Навье-Стокса относятся к гидродинамике, а на практике могут описать поведение вещества в земной магме или пригодиться в предсказании погоды. Но все эти проблемы все еще ищут своего доказательства или опровержения. Кроме одной.
Теорема Пуанкаре
Объяснить простыми словами, в чем заключается эта проблема, довольно непросто, но попробовать можно. Представим себе сферу, к примеру, мыльный пузырь. Все точки его поверхности равноудалены от его центра, который ей не принадлежит. Но это двумерное тело, а гипотеза говорит о трехмерном. Это представить уже невозможно, но на то у нас и есть теоретическая математика. При этом, разумеется, все точки этого тела также будут удалены от центра.
История
Французский математик Анри Пуанкаре занимался самыми разными областями науки. О его достижениях может сказать, к примеру, тот факт, что совершенно независимо от Альберта Эйнштейна он выдвинул основные положения специальной теории относительности. В 1904 году он поднял проблему доказательства того, что любое трехмерное тело, обладающее некоторыми свойствами сферы, ею и является с точностью до деформации. Позднее она была расширена и обобщена, и стала частным случаем гипотезы Терстона, сформулированной в 1982 году.
Формулировка
Пуанкаре изначально оставил такое утверждение: всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере. В дальнейшем оно было расширено и обобщено. И все же на протяжении длительного времени именно изначальная задача вызывала больше всего проблем, и была решена лишь через 100 лет после ее появления.
Интерпретация и смысл
О том, что такое гомеоморфность, речь уже шла. Теперь стоит поговорить о компактности и односвязности. Первое означает лишь, что многообразие имеет ограниченные размеры, не может быть непрерывно и бесконечно растянуто.
Доказательство
Не стоит думать, что из десятков математиков, работавших по всему миру, никто не продвинулся ни на йоту, занимаясь этой проблемой. Наоборот, прогресс был, и в конце концов он привел к результату. Сам Пуанкаре не успел закончить работу, но его исследования серьезно продвинули всю топологию.
В 1982 году и для 4 было найдено доказательство, оставалось только 3. В том же году Терстон сформулирован гипотезу о геометризации, при этом теория Пуанкаре стала ее частным случаем.
На 20 лет гипотеза Пуанкаре была как будто забыта. В 2002 году российский математик Григорий Перельман представил решение в общих чертах, спустя полгода сделав некоторые дополнения. Уже позже это доказательство проверяли и доводили «до блеска» американские и китайские ученые. А сам Перельман словно потерял к проблеме весь интерес, хотя он решил более общую задачу о геометризации, для которой гипотеза Пуанкаре является лишь частным случаем.
Признание и оценки
Разумеется, это сразу стало сенсацией, ведь решение одной из Проблем Тысячелетия просто не могло оказаться незамеченным. Еще больше удивления вызывал тот факт, что Григорий Перельман отказался от всех наград и премий, сообщив, что ему и так прекрасно живется. В умах обывателей он сразу стал примером того самого полусумасшедшего гения, которого интересует только наука.
Все это вызвало много обсуждений в прессе и СМИ, что популярность математика стала его тяготить. Летом 2014 года прошла информация о том, что Перельман уехал работать в Швецию, но это оказалось лишь слухами, он все еще скромно живет в Санкт-Петербурге и почти ни с кем не общается. Среди наград, присужденных ему, были не только премия института Клея, но и престижная медаль Филдса, но он отказался от всего. Впрочем, Гамильтон, который по оценкам Перельмана сделал не меньший вклад в доказательство, тоже не был забыт. В 2009 и 2011 годах он также удостоился некоторых престижных наград и премий.
Отражение в культуре
Несмотря на то что для простых обывателей как постановка, так и решение этой проблемы представляют мало смысла, о доказательстве стало известно довольно быстро. В 2008 году по этому поводу японским режиссером Масахито Касуга был снят документальный фильм «Чары гипотезы Пуанкаре», посвященный столетним попыткам решить эту задачу.