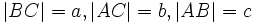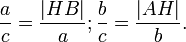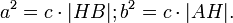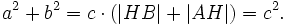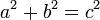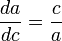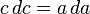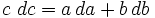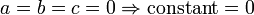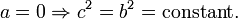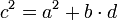в чем заключается теорема пифагора
Теорема Пифагора
Основные понятия
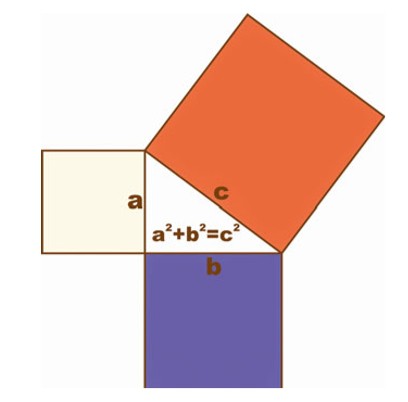
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
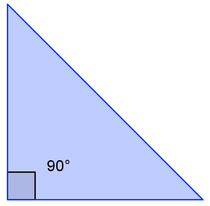
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
Для фигуры со сторонами a, b и c, где c самая длинная сторона действуют следующие правила:
Теорема Пифагора: доказательство
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
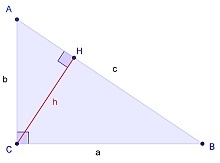
Дано: ∆ABC, в котором ∠C = 90º.
Пошаговое доказательство:
a 2 + b 2 = c * HB + c * AH
a 2 + b 2 = c * (HB + AH)
Обратная теорема Пифагора: доказательство
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такая фигура является прямоугольной.
Дано: ∆ABC
Доказать: ∠C = 90º
Пошаговое доказательство:
Обратная теорема доказана.
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 10 см. Какое значение у гипотенузы?
значит c 2 = a 2 + b 2 = 6 2 + 10 2 = 36 + 100 = 136
Задание 2. Является ли фигура со сторонами 8 см, 9 см и 11 см прямоугольным треугольником?
Ответ: треугольник не является прямоугольным.
Пифагор и его теорема
Пифагору (570—490 гг. до н. э.) принадлежит доказательство знаменитой теоремы о том, что сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
Пифагор родился на острове Самос. Считается, что он побывал и в Египте, и в Вавилоне, но в конце концов поселился в Кротоне — греческой колонии на юге Италии. Там он основал пифагорейский религиозно-мистический союз. Его члены были вегетарианцами, проповедовали аскетизм и считали основой всего число. Среди последователей Пифагора были знатные люди, которые практически захватили власть в Кротоне. Это вызвало недовольство, наука смешалась с политикой, и Пифагору пришлось покинуть город. А после его смерти пифагорейский союз был разгромлен.
Теорема Пифагора
Теорема Пифагора широко применяется на практике, например в мобильной связи. Нужно определить высоту АВ антенны (вышки), чтобы сигнал от неё передавался на расстояние 30 км, до точки С.
ВС — касательная к окружности Земли, следовательно, она перпендикулярна радиусу Земли ОС. Имеется прямоугольный треугольник ВСО, его гипотенуза — ОА + АВ (высота антенны + радиус Земли 6371 км). Известна длина его катетов:
ВС — 30 км, СО — 6371 км, вычисляем длину гипотенузы:
302 + 63712 = 900 + 40589641 = 405905541 (квадрат длины гипотенузы).
Длина гипотенузы: V40590541 = 6371,070632162227 км.
Высота антенны: 6371,070632162227 — 6371 = 0,070632162227 км = 70 м.
Теорема Пифагора.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение
между сторонами прямоугольного треугольника.
Будет полезно сохранить таблицу Пифагора.
Считается, что доказана греческим математиком Пифагором, в честь которого и названа.
Геометрическая формулировка теоремы Пифагора.
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов,
построенных на катетах.
Алгебраическая формулировка теоремы Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
Обе формулировки теоремы Пифагора эквивалентны, но вторая формулировка более элементарна, она не
требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и
Обратная теорема Пифагора.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то
Для всякой тройки положительных чисел a, b и c, такой, что

существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Теорема Пифагора для равнобедренного треугольника.
Теорема Пифагора для равностороннего треугольника.
Доказательства теоремы Пифагора.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема
Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие
можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:
доказательства методом площадей, аксиоматические и экзотические доказательства (например,
с помощью дифференциальных уравнений).
1. Доказательство теоремы Пифагора через подобные треугольники.
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся
напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим
её основание через H.
Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC.


или 
2. Доказательство теоремы Пифагора методом площадей.
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они
используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

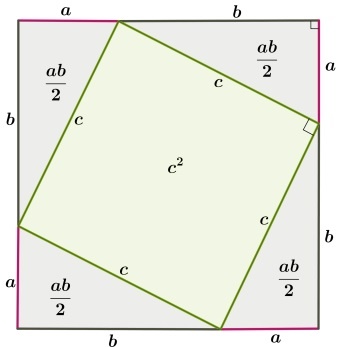
треугольника так, как показано на рисунке
Четырёхугольник со сторонами c – квадратом,
так как сумма двух острых углов 90°, а
развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны,
площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и
Что и требовалось доказать.
3. Доказательство теоремы Пифагора методом бесконечно малых.
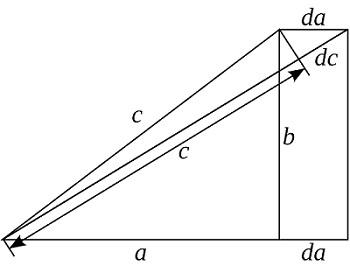
Рассматривая чертёж, показанный на рисунке, и
записать следующее соотношение для бесконечно
малых приращений сторон с и a (используя подобие
Используя метод разделения переменных, находим:
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:
Интегрируя данное уравнение и используя начальные условия, получаем:
Таким образом, мы приходим к желаемому ответу:
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной
пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми
вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения
(в данном случае катет b). Тогда для константы интегрирования получим:
Пифагора теорема
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.
Содержание
Формулировки
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.
Обратная теорема Пифагора:
Доказательства
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например с помощью дифференциальных уравнений).
Через подобные треугольники
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения
Доказательства методом площадей
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.
Доказательство через равнодополняемость
Что и требовалось доказать.
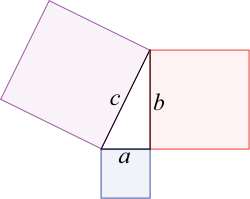
Доказательства через равносоставленность
Пример одного из таких доказательств указан на чертеже справа, где квадрат, построенный на гипотенузе, перестановкой преобразуется в два квадрата, построенных на катетах.
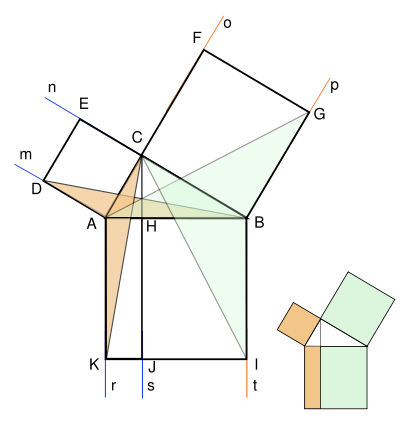
Доказательство Евклида
Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.
Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.
Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.
Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB=AK,AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).
Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.
Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше.
Доказательство Леонардо да Винчи
Главные элементы доказательства — симметрия и движение.
Доказательство методом бесконечно малых
Следующее доказательство при помощи дифференциальных уравнений часто приписывают известному английскому математику Харди, жившему в первой половине XX века.
Рассматривая чертёж, показанный на рисунке, и наблюдая изменение стороны a, мы можем записать следующее соотношение для бесконечно малых приращений сторон с и a (используя подобие треугольников):
Пользуясь методом разделения переменных, находим
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов
Интегрируя данное уравнение и используя начальные условия, получаем
c 2 = a 2 + b 2 + constant.
Таким образом, мы приходим к желаемому ответу
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения (в данном случае катет b ). Тогда для константы интегрирования получим
Вариации и обобщения
История
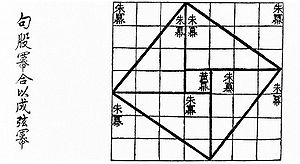
В древнекитайской книге Чу-пей говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.
Доказательства теоремы Пифагора
Этот одна из базовых теорем евклидовой геометрии, определяющая соотношение между сторонами в прямоугольном треугольнике. Несложность доказательства и широкое применение обеспечили ей массовую известность.
Теорема Пифагора — краткая история
Соотношение между сторонами прямоугольного треугольника в том или ином виде было известно многим древним цивилизациям (египетской, шумерской и др.), но первая известная формулировка принадлежит греческому философу и математику Пифагору в V в. до н.э. Об этом известно из труда «Начала», который написал Евклид приблизительно в 300 г. до н. э.
Теорема Пифагора используется для доказательства многих других теорем геометрии. Математиками разработано несколько обобщений, например, для произвольных треугольников, для многомерных пространств. При этом, теорема Пифагора выполняется только в евклидовых геометриях, в иных случаях она не действует.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формулировка теоремы
Изначальная (геометрическая) формулировка Пифагора гласила:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Позднее появился алгебраический вариант:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.
Уравнение
В виде формулы теорема Пифагора записывается следующим образом:
Доказательство через подобные треугольники
Это доказательство – одно из наиболее простых, так как является прямым следствием аксиом и не оперирует понятием площади.
Имеется прямоугольный треугольник ABC, где C = 90º. Высота, проведенная из прямого угла пересечет гипотенузу в точке H.
Полученные треугольники ACH и CHB подобны треугольнику АВС по двум углам. Отсюда получаем:
CB 2 =ABxHB, AC 2 =ABxAH
Сложив между собой квадраты катетов, получаем:
AC 2 +CB 2 =ABx(HB+AH)=AB 2
Это и требовалось доказать.
Другие способы доказательства теоремы
Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.
Методом площадей
Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:
Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.
Площадь внешнего квадрата включает в себя:
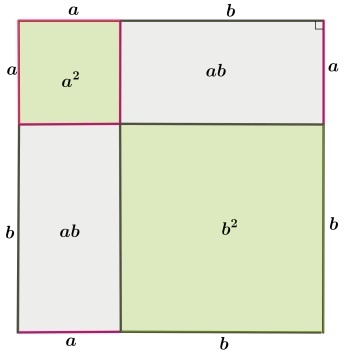
Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.
Методом бесконечных малых
Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.
В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем
Разделяя переменные составляется дифференциальное уравнение:
Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:
определяя из начальных условий константу интегрирования, получим:
a = 0 ⇒ c 2 = b 2 = const
Таким образом мы определяем, что
Следствие из теоремы Пифагора
Его так же называют обратной теоремой Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то такой треугольник прямоугольный.
В алгебраическом виде это можно представить так:
c2=a2+b2, где:
Применение теоремы
Благодаря своей универсальности, теорема Пифагора находит себе применение в разных областях математики и других наук. К числу преимуществ ее применения относится прозрачность производимых вычислений.
Расстояние между точками
Одно из главных применений – это определение расстояния между двумя точками в прямоугольной системе координат:
Евклидова метрика
В этом случае с помощью теоремы Пифагора находится расстояние в многомерном пространстве:
Теория чисел
Арифметическим аналогом теоремы Пифагора стали пифагоровы тройки чисел.
Пифагоровы тройки – группа из трех натуральных чисел x, y и z, удовлетворяющих равенству x2+y2=z2.
Например, к таким числам можно отнести группы (3, 4, 5), (6, 8, 10), (5, 12, 13) и другие. Пифагоровы тройки широко применяются в разных областях деятельности, например, в программировании и криптографии.
Примеры решения задач
Задача 1
В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.
Решение
Для нахождения ответа подставим в формулу исходные значения:
Задача 2
Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.
Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:
Задача 3.
Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.
Решение
Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.