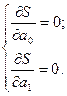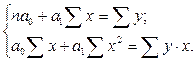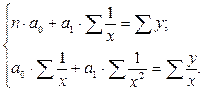в чем заключается сущность использования регрессионных уравнений
Сущность регрессионного анализа. Уравнение регрессии. Метод наименьших квадратов
Регрессионный анализ заключается в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения. До регрессионного анализа следует проводить корреляционный анализ, в процессе которого оценивается степень тесноты статистической связи между исследуемыми переменными. От степени тесноты связи зависит прогностическая сила регрессионной модели.
Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака от факторных признаков.
Уравнение регрессии или модель связи социально-экономических явлений выражается функцией. Различают парную (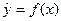
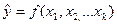
) и множественную (
) регрессии.
Парная регрессий описывает связь между двумя признаками (результативным и факторным). Множественная регрессия описывает связь между результативным признаком и двумя и более факторными признаками.
Изучение модели парной регрессии является базовым во всем курсе эконометрики. Обычно она применяется в том случае, когда из всего круга факторов, влияющих на результат, можно выделить один, оказывающий наиболее сильное воздействие. Он и берется в качестве объясняющей переменной х.
Представим, что есть два ряда данных:
| x1 | x2 | x3 | … | хn |
| y1 | y2 | y3 | … | yn |
где n – число наблюдений.
Каждое из наблюдений характеризуется двумя переменными xi, yi. Число наблюдений n должно в шесть-семь раз превышать число параметров при переменной х в уравнении регрессии. Таким образом, для изучения линейной регрессии число наблюдений должно быть не менее семи.
В парной линейной регрессии связь между переменными определяется следующим образом:
,
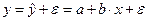
где у – зависимая (объясняемая) переменная, реальная, фактическая, эмпирическая;
х – независимая (объясняющая) переменная;
– зависимая переменная, рассчитанная по уравнению регрессии, теоретическая;
а, b – константы, параметры уравнения линейной регрессии;
– случайная компонента, возмущение.
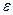
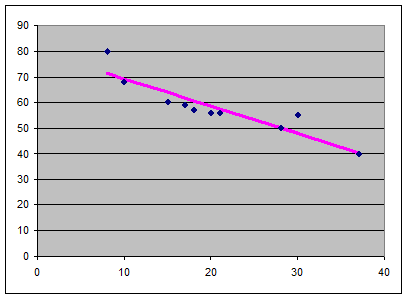
Каждую пару наблюдений (хi;yi) можно представить в виде точки на плоскости. Такое графическое изображение наблюдений называется полем корреляции или диаграммой рассеяния. Выбранный тип функции (прямая, парабола, гипербола и т.д.) должен проходить через большее количество точек или как можно ближе к ним.
В каждом из наблюдений величину случайной компоненты можно определить как разность между фактическим значением результата и рассчитанным по уравнению регрессии:
.
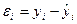
Если на графике все точки совпадут с линией регрессии, то между результативным признаком у и фактором х существует функциональная зависимость, и выполняется равенство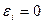 
для каждого наблюдения i=1,2,…,n.
Данные, которые описывают экономические процессы, не могут иметь строгую функциональную зависимость, поскольку на результативный признак в экономике влияет большое количество факторов и случайных процессов, и все они не могут быть учтены в модели.
В парной регрессии выбор вида математической функции 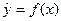может быть осуществлен с помощью следующих методов:
— графического (с помощью построения поля корреляции и подбора функции, график которой проходит через большее количество точек или как можно ближе к ним);
— аналитического (исходя из экономической теории изучаемой взаимосвязи и опыта подобных предыдущих исследований);
— экспериментального (посредством перебора нескольких функций, построения нескольких уравнений регрессии и выбора того уравнения, при котором остаточная дисперсия минимальна).
После того как выбран вид уравнения регрессии (прямая линия, парабола, гипербола и т.д.) находят значения параметров модели, для линейной регрессии – это а0 и а1. Для этого используют метод наименьших квадратов. В основу этого метода положена идея минимизации суммы квадратов отклонений фактических значений у от их выравненных (теоретических) значений , т.е.
,
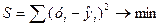
где уi – фактические значения результативного признака;
– теоретические значения результативного признака, найденные по уравнению регрессии.
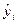
Если регрессия линейная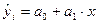 
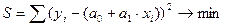
, то
.
Рассматривая сумму S в качестве функции параметров а0 и а1 (значения хi и уi в функции S являются постоянными величинами), определяют частные производные по а0 и а1 и приравнивают их к нулю, поскольку в точке экстремума производная функции равна нулю:
Так, если связь между признаками линейная, то система уравнений для нахождения параметров уравнения регрессии примет вид:
После решения системы относительно а0 и а1 находят уравнение регрессии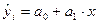 
.
Если связь между признаками у и х описывается уравнением параболы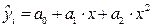 
, то система нормальных уравнений примет вид:
Если связь описывается уравнением гиперболы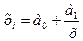 
, система нормальных уравнений следующая:
Вернемся к парной линейной регрессии. Решая систему уравнений относительно а и b, находят значения указанных параметров. Можно также воспользоваться следующими формулами для определения параметров а и b:
и 
.
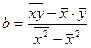
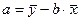
В Excel параметры а и b можно вычислить с помощью функции = ЛИНЕЙН, задав известные значения у и значения х.
Правильность расчетов параметров уравнения регрессии может быть проверена с помощью сравнения сумм:
.
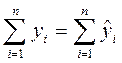
После определения параметров уравнения регрессии а и b записывают уравнение в окончательном виде, например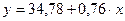 
.
Параметр b (коэффициент при х) определяет, на сколько в среднем изменится у при изменении факторного признака на единицу.
Чем больше величина коэффициента регрессии b, тем значительнее влияние данного факторного признака на моделируемый результативный.
Знак коэффициента регрессии говорит о характере влияния фактора на результативный признак.
Экономическая интерпретация параметров линейного уравнения регрессии дополняется расчетом коэффициента эластичности:
.
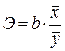
Этот коэффициент показывает, на сколько процентов в среднем изменится у при изменении фактора х на 1%.
R — значит регрессия
Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.
Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.
Введение в регрессионный анализ
Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция 
такая, что сумма квадратов разностей 
минимальна.
Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.
Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений 
вокруг регрессии 
является дисперсия.
Линейная регрессия
Уравнения линейной регрессии можно записать в виде
В матричном виде это выгладит
Случайная величина может быть интерпретирована как сумма из двух слагаемых:
Ограничения линейной регрессии
Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.
Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.
Неоднородность дисперсии
При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.
Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.
Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.
В этой формуле 
— коэффициент взаимной детерминации между 
и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.
Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.
Как преодолеть эти ограничения
Нарушения одной или нескольких ограничений еще не приговор.
К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.
Линейная регрессия плюсов на Хабре
Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.
Загружает данные из tsv файла.
Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.
В первой строке мы задаем параметры линейной регрессии. Строка points
. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points
Перейдем теперь к расшифровке полученных результатов.
Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.
Проверим значения параметров линейной регрессии.
Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.
И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.
В заключение
Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.
Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.
Сущность, виды и значение уравнений регрессии
Под регрессией понимается функция, предназначенная для описания зависимости изменения результативных признаков под влиянием колебаний признаков-факторов. Понятие регрессии введено в статистическую науку по предложению английского ученого Ф. Гальтона.
В корреляционно-регрессионном методе парной корреляционной взаимосвязи соответствует однофакторная регрессионная модель, множественной взаимосвязи – множественная регрессия. Поэтому наличие корреляционной связи между параметрическими признаками позволяет приближению представить значения результативного признака в виде некоторой функции от величины одного или нескольких факторных признаков.
Функцию, показывающую корреляционную зависимость между признаками, принято называть уравнением регрессии. Если оно связывает лишь два признака, то представляет собой уравнение парной регрессии; если отражает зависимость результативного признака от двух, трех и более факторных признаков – это уравнение множественной регрессии.
Ранее было показано, что при выявлении корреляционной формы, связывающей результативный признак с одним факторным, помогает графическое изображение корреляционной связи в виде поля корреляции. Обычно считают, что увеличение результативного и факторного признаков в арифметической прогрессии при прямой связи требует применения линейной, а при обратной – гиперболической регрессии.
Прямая связь, при которой результативный признак увеличивается в арифметической прогрессии, а факторный повышается быстрее признака-результата, требует применения параболической или показательной регрессии. Уравнение множественной регрессии обычно выражается либо прямой, представляющей собой функцию многих переменных, либо степенной функцией.
Составление уравнения регрессии означает прежде всего определение его параметров, используя для этого, где возможно, способ наименьших квадратов, согласно которому сумма квадратов отклонений фактических значений результативного признака от теоретических значений, рассчитанных по уравнению регрессии, должна быть наименьшей, т.е.
(11.7)
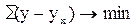
где у – фактические варианты признака-результата; ух – теоретические значения признака-результата.
Это условие приводит к системе нормальных уравнений, решение которых позволяет определить параметры уравнения регрессии. Заметим при этом, что число нормальных уравнений на одно больше числа входящих в уравнение регрессии факторов. Если известны параметры уравнения, то, подставляя в него принятые значения факторных признаков, можно рассчитать теоретическое значение результативного признака, что делает удобным применение корреляционных уравнений при прогнозировании результативных признаков.
Уравнение регрессии может показать связь между признаками более точно, если оно построено на основании достаточно большой статистической совокупности. Но поскольку оно все-таки выражает приближенную меру связи, то уравнение регрессии нередко называют моделью связи между признаками.
Методы регрессионного анализа в Data Science
Накануне запуска курса «Математика для Data Science. Продвинутый курс» мы провели открытый вебинар на тему «Методы регрессионного анализа в Data Science». На нём познакомились с понятием линейных регрессий, изучили, где и как их можно применять на практике, а также узнали, какие темы и разделы математического анализа, линейной алгебры и теории вероятностей используются в этой области. Преподаватель — Петр Лукьянченко, преподаватель НИУ ВШЭ, руководитель технологических проектов.
Если мы говорим о математике в контексте Data Science, мы можем выделить три наиболее часто решаемые задачи (хотя задач, разумеется, больше):
Поговорим об этих задачах подробнее:
Во всех трёх задачах присутствует и оптимизация, и минимизация ошибки, и наличие той или иной модели, которая описывает зависимость переменных. При этом внутри каждой лежит представление данных, которые разложены на векторное описание. Мы же в нашей статье уделим особое внимание разделу, который затрагивает именно регрессионные модели.
Мы уже упомянули, что есть некий набор пар данных: Х и Y. Мы знаем, какие значения принимает Y относительно X. Если Х — это время, то тогда у нас получается модель временного ряда, в котором Y — это, допустим, цена нефти и при этом курс рубля к доллару, а Х — это некоторый период времени с 2014 по 2018:
Рассмотрим следующую иллюстрацию:
Получается, мы выбираем какую-то модель зависимости данных, а виды зависимости между случайными величинами бывают разные. Всё не так уж и очевидно, ведь даже на этих простых рисунках мы видим различные зависимости. Выбрав конкретную зависимость, мы сможем использовать регрессионные методы для калибровки модели.
От того, какую модель вы выберете, будет зависеть качество ваших прогнозов. Если остановиться на линейных регрессионных моделях, то мы предполагаем, что есть некий набор реальных значений:
На рисунке показаны 4 наблюдаемых значения Х1, Х2, Х2, Х4. Для каждого из «иксов» известно значение Y (в нашем случае, это точки: P1, P2, P3, P4). Это точки, которые мы реально наблюдаем на данных. Таким образом, мы получили некий датасет. И по каким-то соображениям мы решили, что линейная регрессия лучше всего описывает зависимость между «иксом» и «игреком». Дальше весь вопрос заключается в том, как построить уравнение прямой линии Y = b1 + b2X, где b2 — коэффициент наклона, b1 — коэффициент пересечения. Весь вопрос заключается в том, какие b2 и b1 лучше всего установить, чтобы эта прямая линия как можно точнее описывала зависимость между этими переменными.
Точки R1, R2, R3, R4 — это значения, которые выдаёт наша модель при значениях X. Что получается? Точки P — точки, которые мы реально наблюдаем (реально собрали), а точки R — это точки, которые мы наблюдаем в нашей модели (те, что она выдаёт). Дальше следует до безумия простая человеческая логика: модель будет считаться качественной тогда и только тогда, когда точки R максимально близки к точкам P.
Если мы построим расстояние между этими точками для одинаковых «иксов» (P1 – R1, P2 – R2 и т. д.), то мы получим то, что называется ошибками линейной регрессии. Мы получим отклонения в линейной регрессии, и эти отклонения называются U1, U2, U3…Un. А ошибки эти могут быть как в плюс, так и в минус (мы могли переоценить или недооценить). Чтобы эти отклонения сравнить, их нужно проанализировать. Здесь применяют очень большой и красивый способ — возведение в квадрат (возведение в квадрат «убивает» знак). А сумму квадратов всех отклонений в математической статистике называют RSS (Residual Sum of Squares). Минимизировав RSS по b1 и минимизировав RSS по b2, мы получаем оптимальные коэффициенты, которые фактически выводятся методом наименьших квадратов.
После того, как мы построили регрессию, определили оптимальные коэффициенты b1 и b2, и у нас есть уравнение регрессии, проблемы на этом не заканчиваются, а задача продолжает развиваться. Дело в том, что если на одном графике пометить саму регрессию, все значения, которые у нас есть, а также средние значения «игреков», то суммы квадратов ошибок можно будет доуточнить.
В то же время полезным считается отображать ошибки предсказания регрессии относительно переменной X. Смотрим рисунок ниже:
Мы получили какую-то регрессию и нарисовали настоящие данные, которые есть. Мы получили расстояние от каждого настоящего значения до регрессии. И нарисовали её относительно нулевого значения для соответствующих значений X. И на рисунке выше мы наблюдаем на самом деле очень плохую картину: ошибки зависят от X. Явно выражена какая-то корреляционная зависимость: чем дальше по «иксу» мы движемся, тем большее значение ошибок. Это очень плохо. Наличие корреляции в этом случае свидетельствует, что мы ошибочно взяли регрессионную модель, и был какой-то параметр, который мы «не додумали» или просто упустили из виду. Ведь если внутрь модели помещены все переменные, ошибки должны быть полностью случайными и не должны зависеть от того, чему равняются ваши факторы. Ошибки должны быть с одинаковым вероятностным распределением, иначе ваши предсказания будут ошибочными. Если вы нарисовали на плоскости ошибки вашей модели и встретили расходящийся треугольник, лучше начать всё с нуля и полностью пересчитать модель.
По анализу ошибок можно даже сразу понять, где просчитались, какой тип ошибки сделали. И вот здесь нельзя не упомянуть теорему Гаусса-Маркова:
Теорема определяет условия, при которых оценки, которые мы получили методом наименьших квадратов, будут являться наилучшими, состоятельными, эффективными в классе линейных несмещённых оценок.
Вывод можно сделать следующий: сейчас мы понимаем, что область построения регрессионной модели — это, в каком-то смысле, кульминация с точки зрения математики, потому что в ней сливаются сразу все возможные разделы, которые могут быть полезны в анализе данных, например: