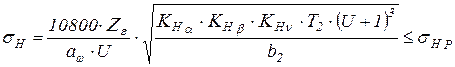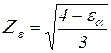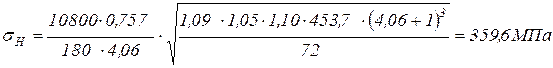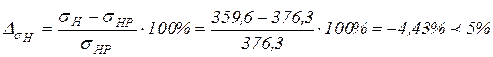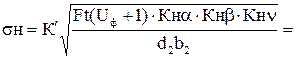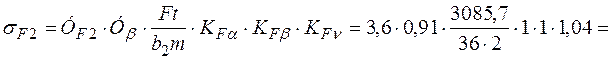в чем заключается проверочный расчет зубчатых передач
Проверочный расчет зубчатого зацепления



¨ Проверочный расчет зубьев на выносливость по контактным напряжениям.
Действительные контактные напряжения определяем по формуле:
где σНР – допустимые контактные напряжения;
Zε – коэффициент, учитывающий степень перекрытия,
Для прямозубых колес:
Для косозубых колес:
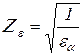
КНα – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;
КНα = 1 для прямозубых колес
Значение КНα для косозубых и шевронных передач определим из таблицы 6.6.
| Окружная скорость V, м/с | Степень точности по нормам плавности (ГОСТ 1643-81) | ||||
| 2,5 | 1,00 | 1,01 | 1,03 | 1,05 | 1,13 |
| 1,00 | 1,02 | 1,05 | 1,09 | 1,16 | |
| 1,01 | 1,03 | 1,07 | 1,13 | — | |
| 1,01 | 1,04 | 1,09 | — | — | |
| 1,02 | 1,05 | 1,12 | — | — | |
| 1,02 | 1,06 | — | — | — |
КНβ – коэффициент учитывающий неравномерность распределения нагрузки по ширине венца зубчатого колеса берут из таблицы 6.7:
| Расположение зубчатых колес относительно опор | Твердость НВ поверхностей зубьев | |
| ≤ 350 | > 350 | |
| Симметричное | 1,0…1,15 | 1,05…1,25 |
| Несимметричное | 1,10…1,25 | 1,15…1,35 |
| Консоль | 1,20…1,35 | 1,25…1,45 |
КНV – динамический коэффициент определяют в зависимости от степени точности передачи, окружной скорости и твердости рабочих поверхностей.
Значения коэффициента КНV определяют из таблицы 6.8:
| Степень точности по ГОСТ 1643-81 | Твердость на поверхности зубьев колеса | Значения КНV при V, м/с | |||
| >350 НВ | 1,02/1,01 | 1,06/1,03 | 1,10/1,04 | 1,16/1,06 | 1,20/1,08 |
| ≤ 350 НВ | 1,03/1,01 | 1,09/1,03 | 1,16/1,06 | 1,25/1,09 | 1,32/1,13 |
| >350 НВ | 1,02/1,01 | 1,06/1,03 | 1,12/1,05 | 1,19/1,08 | 1,25/1,10 |
| ≤ 350 НВ | 1,04/1,02 | 1,12/1,06 | 1,20/1,08 | 1,32/1,13 | 1,40/1,16 |
| >350 НВ | 1,03/1,01 | 1,09/1,03 | 1,15/1,06 | 1,24/1,09 | 1,30/1,12 |
| ≤ 350 НВ | 1,05/1,02 | 1,15/1,06 | 1,24/1,10 | 1,38/1,15 | 1,48/1,19 |
| >350 НВ | 1,03/1,01 | 1,09/1,03 | 1,17/1,07 | 1,28/1,11 | 1,35/1,14 |
| ≤ 350 НВ | 1,06/1,02 | 1,12/1,06 | 1,28/1,11 | 1,45/1,18 | 1,56/1,22 |
Примечание. В числителе приведены значения для прямозубых, в знаменателе – для косозубых зубчатых колес.
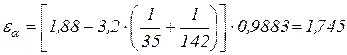
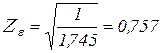
Из соответствующих таблиц согласно нашим условиям определим значения коэффициентов:
Подставив значения в формулу, получим:
Отклонение величины действительного контактного напряжения от допускаемого определим по формуле:
По принятым в общем машиностроении нормам для σН допускается отклонение ± 5%. Если отклонения выходят за указанные пределы, то размеры и другие параметры передачи необходимо откорректировать. При больших отклонения порядка ± 10…15% можно рекомендовать:
— в небольших пределах изменить ширину колеса b (при перегрузках – увеличить, при недогрузках – уменьшить);
— изменить степень точности изготовления колес;
— в тех случаях, когда нежелательно изменять ширину колеса или степень точности, можно выбрать другой режим термической обработки поверхностей зубьев и соответственно изменить твердость поверхностей зубьев, что приводит к увеличению или уменьшению σНР.
— при больших отклонениях σН от допускаемого значения расчет проводят заново после изменения межосевого расстояния.
¨ Проверка на контактную прочность по кратковременным перегрузкам.
Расчетное максимальное контактное напряжение при перегрузке найдем по формуле:
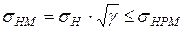
где σНРМ – максимальные допустимые контактные напряжения;
σН – действительные контактные напряжения;
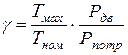
где 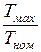
Рдв – стандартная мощность выбранного электродвигателя;
Рпотр. – потребная мощность электродвигателя.
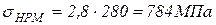
где σт – предел текучести материала зубчатого колеса.
Проверочные расчёты зубчатых передач
3.3.1 Проверочный расчёт цилиндрических зубчатых передач.
Порядок проверочного расчета цилиндрических зубчатых передач представим в виде таблицы 3.4.
Таблица 3.4 – Порядок проверочного расчета цилиндрических зубчатых передач
| Параметр | Обозна-чение | Определение параметра |
| По контактным напряжениям | ||
| Коэффициент торцового перекрытия (только для косозубой передачи) | 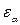 | 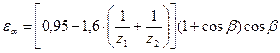 . . |
| Коэффициент повышения прочности косозубых передач по контактным напряжениям (только для косозубой передачи) | 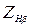 | 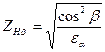 . . |
| Окружная скорость | 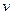 | 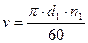 . . |
| Коэффициент динамической нагрузки | 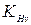 | Выбираем по таблице А.7 [1, таблица 8.3] в зависимости от степени точности, твердости поверхности зубьев и окружной скорости 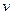 . . |
| Коэффициент расчётной нагрузки | 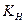 | 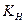 = = 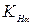 · · 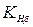 · · 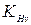 . . |
| Угол профиля | 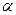 | 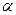 = 20º. = 20º. |
| Контактные напряжения | 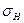 | Для прямозубых передач 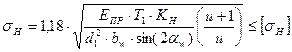 ; для косозубых передач ; для косозубых передач 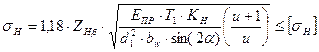 . . |
Продолжение таблицы 3.4
| Недогрузка (перегрузка) | 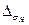 | 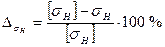 . Если недогрузка больше 5 % или перегрузка больше 3 % то производим корректировку ширины . Если недогрузка больше 5 % или перегрузка больше 3 % то производим корректировку ширины 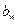 по формуле по формуле 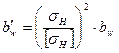 и пересчитываем и пересчитываем 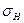 . . |
| По напряжениям изгиба | ||
| Эквивалентное число зубьев для шестерни и колеса (только для косозубой передачи) | 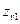 , , 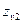 | 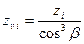 . . |
| Коэффициент формы зуба для шестерни и колеса | 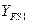 , , 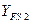 | Выбираем по графику на рисунке А.3 [1, рисунок 8.20] при коэффициенте смещения x = 0 при числе зубьев  ‑ для прямозубых передач и ‑ для прямозубых передач и 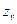 ‑ для косозубых. ‑ для косозубых. |
| Определяем отношение | 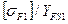 , , 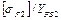 | В дальнейшем расчёт ведём при том 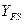 , для которого отношение получилось меньше. , для которого отношение получилось меньше. |
| Коэффициент повышения изгибной прочности вследствие наклона контактной линии к основанию зуба (только для косозубой передачи) | 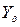 | 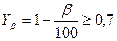 . . |
| Коэффициент повышения прочности косозубых передач по напряжениям изгиба (только для косозубой передачи) | 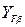 | 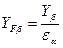 . . |
| Коэффициент неравномерности нагрузки | 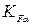 | 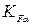 = = 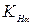 . . |
| Коэффициент концентрации нагрузки | 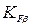 | Выбираем по графикам на рисунке А.2 [1, рисунок 8.15], в зависимости от твердости поверхности зубьев, вида редуктораи коэффициента 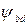 . . |
| Коэффициент динамической нагрузки | 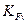 | Выбираем по таблице А.7 [1, таблица 8.3] в зависимости от степени точности, твердости поверхности зубьев и окружной скорости 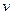 . . |
| Коэффициент расчётной нагрузки | 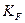 | 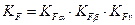 . . |
| Окружное усилие | 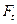 | 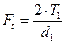 . . |
Окончание таблицы 3.4
| Напряжения изгиба | 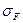 | Для прямозубых передач 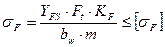 ; Для косозубых передач ; Для косозубых передач 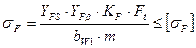 . Если условие не выполняется, то производим корректировку ширины шестерни по формуле . Если условие не выполняется, то производим корректировку ширины шестерни по формуле 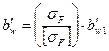 , но таким образом, чтобы выполнялось условие , но таким образом, чтобы выполнялось условие 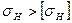 . . |
3.3.2 Проверочный расчёт конической прямозубой передачи.
Порядок проверочного расчета конических прямозубых передач представим в виде таблицы 3.5.
Таблица 3.5 – Порядок проверочного расчета конических прямозубых передач
| Параметр | Обозна-чение | Определение параметра |
| По контактным напряжениям | ||
| Степень точности | 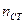 | Выбираем по таблице А.5 [1, таблица 8.2]. |
| Окружная скорость | 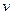 | 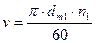 . . |
| Коэффициент динамической нагрузки | 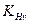 | Выбираем по таблице А.7 [1, таблица 8.3] в зависимости от степени точности, твердости поверхности зубьев и окружной скорости (при этом степень точности условно понижают на 1 единицу). |
| Коэффициент расчётной нагрузки | 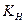 | 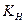 = = 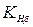 · · 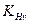 . . |
| Угол профиля | 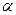 | 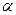 = 20º. = 20º. |
Продолжение таблицы 3.5
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Проверочный расчет зубчатых соединений



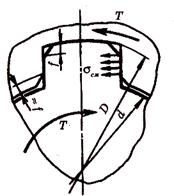
Прочность – основной критерий работоспособности зубчатых соединений. Эти соединения аналогично шпоночным выбирают по таблицам стандартов в зависимости от диаметра вала, а затем выполняют проверочный расчет. Проверочный расчет зубчатых соединений выполняют на смятие. Проверку зубьев на срез не производят. В упрощенной расчетной модели (рисунок 6.4) принято равномерное распределение нагрузки по длине зубьев. При этом получают
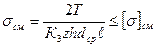
где Т –наибольший крутящий момент из длительно действующих; Кз = 0,7 – 0,8 – коэффициент неравномерности нагрузки по зубьям; z – число зубьев; h – рабочая высота зубьев; 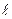
Рисунок 6.4 – Расчетная схема прямобочного шлицевого соединения
Для прямобочных зубьев
для эвольвентных зубьев
где т – модуль зубьев; 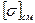
В таблице 6.2 приведены значения 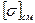
Например, в станкостроении рекомендуют более низкие значения: 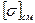
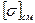
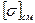
Таблица 6.2 –Допускаемые напряжения на смятие
| Тип соединения | Условия эксплуатации | [σ]см, МПа | |
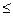 НВ 350 НВ 350 | 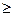 HRC 40 HRC 40 | ||
| Неподвижное | а б в | 35. 50 60. 100 80. 120 | 40. 70 100. 140 120. 200 |
| Подвижное без нагрузки (например, коробки скоростей) | а б в | 15. 20 20. 30 25. 40 | 20. 35 30. 60 40. 70 |
| Подвижное под нагрузкой | а б в | — — — | 3. 10 5. 15 10. 20 |
Примечания: а – тяжелые условия эксплуатации – нагрузка знакопеременная с ударами; вибрации большой частоты и амплитуды; плохие условия смазки в подвижных соединениях; невысокая точность изготовления; б – условия эксплуатации средние; в – условия эксплуатации хорошие. Меньшие значения – для легких режимов нагрузки.
Проверочный расчет зубчатой передачи
5.1. Проверим межосевое расстояние :
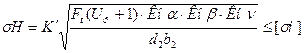
где K¢ – вспомогательный коэффициент. Для косозубых передач K¢=376 (для
Ft = 2Т2 × 10 3 / d2 – окружная сила в зацеплении, Н для нашего случая, где Т2 = Т3 имеем,
Ft = 2Т3 × 10 3 / d2= 2 × 0,307 × 10 3 × 10 3 /198,98 = 3085,7 Н.
Кнa – коэффициент, учитывающий распределение нагрузки между зубьями: определяем по графику (рис. 5) в зависимости от окружной скорости колес
ν = w3 d2 / (2 × 10 3 ), м/с и степени точности передачи (табл. 6):
ν= 10,23×198,98 / (2 × 10 3 )= 1,02 м/с.
Кнn – коэффициент динамической нагрузки, зависящий от окружной
скорости колес и степени точности передачи (табл. 6)
Кнβ, Uф, d2, b2 – значения перечисленных величин определяли ранее (см.
раздел 3, п.1, п.8, п.10, п.2).
Подставим в формулу (36) полученные величины, имеем, что
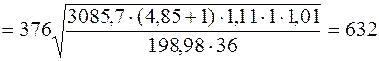
Полученное значение контактного напряжения [s]н меньше допускаемого [sн] = 637,9 МПа.
Определим степень недо грузки по контактным напряжениям :
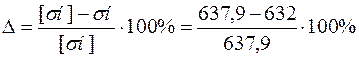
5.3. Проверим напряжение изгиба зубьев шестерни sF1 и колеса sF2, МПа :
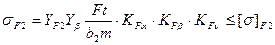
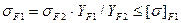
где m – модуль зацепления, m = 4 мм по расчетам ;
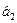
зависит для косозубых от степени точности передачи, определяемой по
Для прямозубых КFa = 1, задается.
КFβ – коэффициент неравномерности нагрузки по длине зуба, выбираем аналогично КFβ, КFβ = 1;
УF1 и УF2 – коэффициенты формы зуба шестерни и колеса.
где β – угол наклона зубьев, определяемый ранее.
Подставим в формулу (37) и (38) известные величины и определим :
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
В чем заключается проверочный расчет зубчатых передач
Классификация передач. По форме различают цилиндрические, конические, реечные, эллиптические, фигурные зубчатые колеса и с неполным числом зубьев. В зависимости от взаимного расположения; зубчатых колес различают зубчатые передачи с внешним и внутренним зацеплением, а также разделяются на открытые и закрытые (рис. 81).
Преимущества. Важнейшие: компактность, высокий КПД, постоянство передаточного числа, большая долговечность и надежность в работе, возможность осуществления передачи практически любых мощностей при практически любых скоростях и передаточных отношениях, простота обслуживания. Высокая технологичность, которая обусловлена высокопроизводительным специальным оборудованием и технологиями.
Недостатки. Высокие требования к качеству изготовления и монтажа. Шум при больших скоростях. Концентрация напряжений в эвольвентных передачах при точечном контакте и чувствительность к ошибкам монтажа в передачах с линейным контактом. Поэтому для реализации преимуществ при изготовлении деталей необходимо применять высококачественные материалы и технологии изготовления.
Сферы применения. 3убчатые передачи нашли самое широкое распространение среди механических передач в машинах различных отраслей. Назначение и конструкции зубчатых передач разнообразны. Их применяют во многих приборах и почти во всех машинах, в том числе и самых тяжелых и мощных для передачи мощностей до 65 тыс.кВТ (65МВт), с диаметром колес от долей миллиметра до 6м и более. Окружная скорость зубьев может достигать 270м/с. Передаточные отношения для открытой передачи принимают 


Геометрический расчет. Передаточное отношение передачи

где 
Номинальные значения передаточных чисел и зубчатых редукторов общего назначения, выполненных в виде самостоятельных агрегатов стандартизированы:
1-й ряд 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0;12,5.
2-й рад 1,12; 1,40; 1,80; 2,24; 2,80; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2.
При выборе стандартных параметров первый ряд предпочтительнее второго, а принятые значения передаточных чисел не должны отличаться от расчетных не более чем на 3%.
Расстояние между осями зубчатых колес цилиндрической передачи по межосевой линии называется межосевым расстоянием:

Стандартизированы номинальные значения межосевых расстояний aw, мм:
1-й ряд 40; 50; 63; 80100; 125; 160; 200; 250; 315; 400; 500; 630; 800
Межосевое расстояние цилиндрической зубчатой передачи, равное полусумме делительных диаметров колеса d2 и шестерни 

Делительные диаметры для зубчатых колес прямозубой передачи
для косозубой и шевронной

1-й ряд 1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25;
2-й ряд 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22; 28.
Ширина венца цилиндрического зубчатого колеса определяется по одной из формул


где 

Коэффициенты 


Значения коэффициентов ширины венца зубчатых колес 
Рис. 82. Обозначения элементов зубчатого зацепления.
Для заданного числа зубьев 




Параметр
Шестерня
Колесо
Диаметр вершин зубьев
Диаметр впадин зубьев
Делительный угол профиля в торцевом сечении
Коэффициент торцевого перекрытия
Рабочая ширина зубчатого венца
Коэффициент осевого перекрытия (при ширине венца 
Основной угол наклона
Кинематический и силовой расчет. Расчетная окружная скорость v цилиндрической передачи:
— шестерни 
— колеса 
Окружная сила цилиндрической зубчатой передачи Ft

где 
Сила давления между зубьями в цилиндрической прямозубой передаче

Радиальная сила в цилиндрической передаче

Осевая сила, действующая на колесо косозубой цилиндрической передачи

Критерии работоспособности зубчатых передач. Учитывая виды повреждений критериями работоспособности зубчатых передач являются контактная и изгибная прочность зубьев. Проектный расчет закрытых передач малой и средней твердости выполняется на контактную выносливость. Расчет на изгибную прочность зубьев в этом случае выполняется как проверочный. Для зубчатых колес высокой прочности (
Проектные расчеты зубчатых передач.
Расчет зубьев на контактную прочность выполняют для зацепления в полюсе, так как выкрашивание зубьев начинается у полюсной линии. По зависимости для проектного расчета на контактную прочность зубьев определяется межосевое расстояние

где 




Рис.84. Коэффициенты неравномерности распределения нагрузки по длине контактных линий 
Коэффициент ширины венца по межосевому расстоянию 





Допускаемое контактное напряжение

При известном межосевом расстоянии ориентировочное значение модуля передачи определяется по зависимости

где 


Значение модуля зацепления полученное по формуле (14.27) округляется до ближайшего стандартного значения. После определения значений межосевого расстояния 

Проверочные расчеты зубчатых передач.
Расчет зубьев на контактную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости
— для прямозубых передач

— для косозубых передач

где 


Таблица 14.3 Значения коэффициента динамических нагрузок
Степень точности
Твердость поверхностей зубьев
υ, м/с
















































Коэффициент неравномерности распределения нагрузки для прямозубых передач принят КНа = 1, а для косозубых коэффициент 

При действии на зубья кратковременных перегрузок выполняется проверка рабочих поверхностей зубьев на контактную прочность по максимальному контактному напряжению:

Расчет зубьев на изгибную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости

где 




При подстановке окружной силы 

Коэффициент, учитывающий перекрытие зубьев

При приближенных расчетах для для косозубых передач и прямозубых передач принимают 
Коэффициент наклона зубьев для прямозубых передач 

при 
Коэффициент неравномерности распределения нагрузки для прямозубых передач принят 


Таблица 14.4 Значения коэффициента динамических нагрузок
Степень точности
Твердость поверхностей зубьев