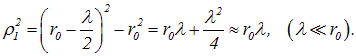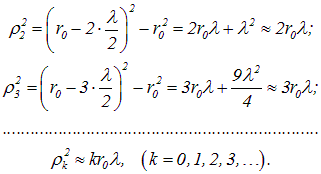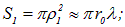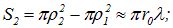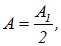в чем заключается принцип построения зон френеля

В чем заключается принцип теории Гюйгенса Френеля

Как известно, свет проявляет свойства, волны и частицы. Одна из теорий, описывающих его поведение — это волновая теория света. Важнейший постулат этой теории — принцип Гюйгенса-Френеля. Он описывает и объясняет распространение волн, частным случаем которых и является свет — электромагнитное излучение в оптическом диапазоне.

Суть принципа Гюйгенса-Френеля

Это утверждение объясняет и описывает то, как распространяются колебания, например, свет. Оно состоит из двух частей. Первую часть (принцип Гюйгенса) предложил Христиан Гюйгенс в 1678 году. Он предположил, что при распространении излучения из каждой точки волнового фронта начинают исходить новые сферические волны.

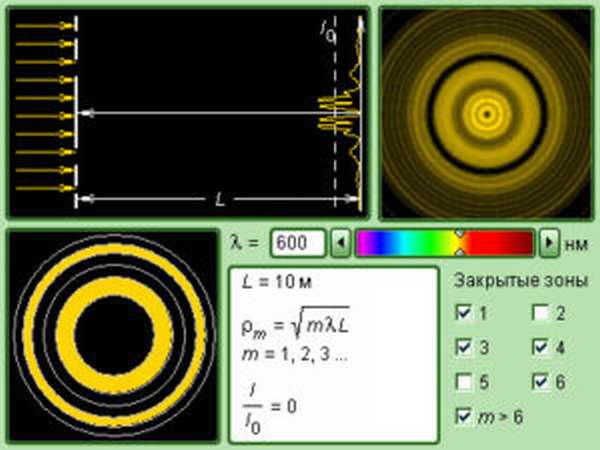
Волновой фронт — это поверхность, на которой возмущение находится в одинаковой фазе. Проще говоря, это граница пространства, в котором уже распространилось возмущение. Например, если бросить камень в воду, пойдут круги — волны. Их фронт в этом случае — это самый внешний круг.

Огюстен Жан Френель в 1815 году развил предположение Гюйгенса.

Важно! Его дополнение заключается в том, что поле, получившееся при распространении возмущения, создается интерференцией вторичных колебаний, которые имеют одинаковую амплитуду. Огибающая вторичных волн дает положение волнового фронта через небольшой промежуток времени.

Интерференция — это наложение волн друг на друга. При этом в одних участках колебания они взаимно усиливают друг друга, в других ослабляют. Поэтому для света получается картина из светлых и темных полосок. Пример этого кольца Ньютона, картина из концентрических кругов, получающаяся, если плоско-выпуклую линзу положить на стеклянную пластинку.

Чтобы можно было наблюдать картину интерференции, излучение должно быть когерентным. Это значит, что оно должно иметь постоянную разность фаз и давать колебания такой же частоты, если их сложить.

Утверждение, сделанное Гюйгенсом, помогало определить только направление распространения возмущения и объясняло распространение света, как его описывает геометрическая оптика. Дополнение принципа Гюйгенса позволяет рассчитывать амплитуду и интенсивность.

Это интересно! Какие бывают системы отсчета в физике и что это такое

Краткая формулировка

Если говорить кратко, этот постулат заключается в следующем. Колебания в любой точке пространства — это результат интерференции возмущений, излученных точками на волновой поверхности.

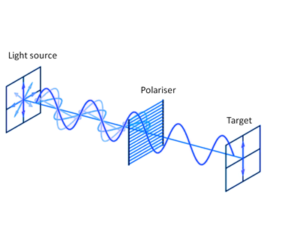
Для любой точки пространства колебания — это наложение вторичных когерентных колебаний, излучаемых точками волнового фронта. Таким образом, в некоторых задачах можно один источник заменить на несколько одинаковых вторичных источников.

Применение

Рассматриваемое утверждение дает возможность объяснить различные оптические явления:

С помощью принципа Гюйгенса-Френеля можно рассчитать амплитуду и интенсивность светового излучения. Для этого используются методы зон Френеля.

Зоны Френеля

Это утверждение важно для решения задач по дифракция света по принципу Гюйгенса-Френеля. Строгое решение таких задач математически очень сложно, поэтому пользуются приближенными методами.

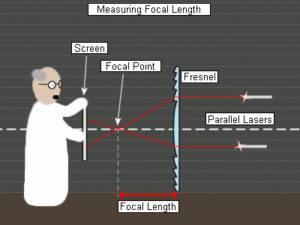
Благодаря открытиям Гюйгенса и Френеля в таких задачах можно заменить один первичный источник совокупностью вторичных источников.

Это существенно облегчает задачу, например, для сферического случая. Такой метод расчета называется методом зон Френеля.

Важно! Зоны Френеля — это участки, на которые делят поверхность, чтобы упростить расчет, например, амплитуды колебаний. На зоны можно разбить любую поверхность, через которую проходит свет.

Сферический случай

В случае сферической волны зоны Френеля выглядят как кольца. Для произвольной точки М их можно построить, проведя из этой точки сферы радиусы, различающиеся на 1/2 длины волны.

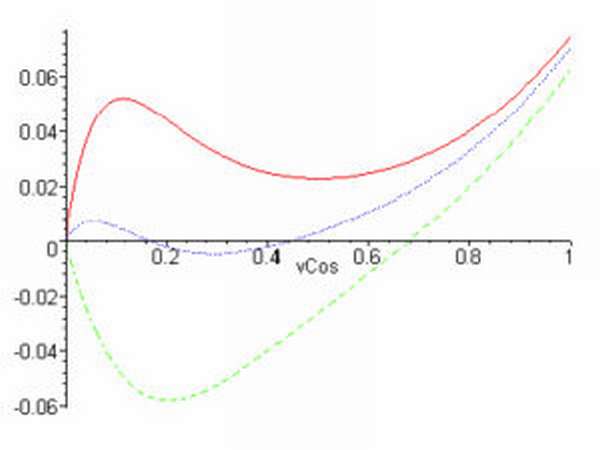
Для сферического случая можно посчитать радиус зоны. Это внешний радиус кольца.

Площади зон Френеля с небольшими номерами примерно одинаковы. Они не зависят от номера зоны m. Они считаются как разница площадей сегментов сферы. Если не углубляться в детали, площади зон Френеля в этом случае находят так. Нужно умножить длину волны на радиус сферического волнового фронта R, на расстояние до точки наблюдения a и на число пи, а затем поделить на сумму R и a.

Зоны Френеля находят применение в зонных пластинках со светлыми и темными кольцами-радиусами, соответствующими размерам зон. Они работают аналогично собирающей линзе.

Это интересно! Квантовые постулаты Нильса Бора: кратко об основных положениях

Дифракция

С помощью этого постулата объясняется дифракция света по принципу Гюйгенса-Френеля — огибание ими небольших предметов. Для света он дает обоснование того, почему возмущения распространяются и в область геометрической тени. Если бы они не огибали предметы, мы бы никогда не увидели полутени, все тени были бы резкими, как предполагает геометрическая оптика. Но реальная картина отличается от предположений геометрической оптики.

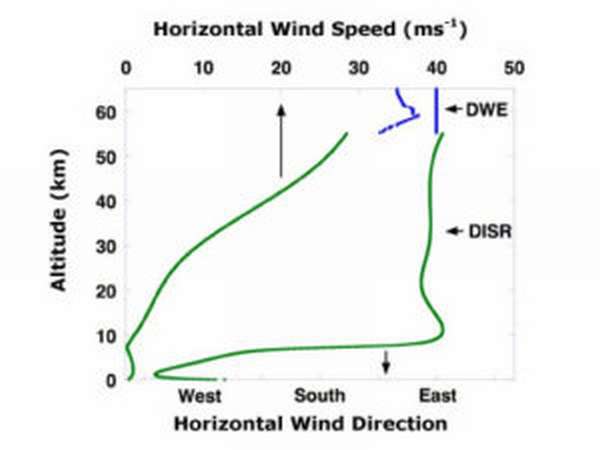
Пример — плоская волна, падающая на плоскость с отверстием. Когда она проходит через отверстие, все точки фронта излучают вторичные сферические колебания. С помощью построения огибающей увидим, что фронт волны оказывается там, куда согласно геометрической оптике свет попадать не должен.

Френель обосновал явление дифракции света по принципу Гюйгенса-Френеля и создал метод ее расчета. Развив принцип Гюйгенса, он установил, что:

Дифракция на прямоугольной щели

Прямоугольную щель можно поделить на N зон в виде узких полосок, параллельных ее длинной стороне. Если наблюдатель находится далеко от источника, то задача сводится к расчету интерференции от N одинаковых источников.

В таком случае интерференционная картина выглядит как светлые и темные полосы. Наиболее яркая светлая полоса — главный максимум — находится в центре.

Преломление

Когда свет попадает из одной среды в другую, например, из воздуха в воду, он меняет направление, т.е. преломляется. Согласно принципу Гюйгенса-Френеля на границе сред из каждой точки исходит вторичное излучение.

Из принципа Гюйгенса можно получить, что показатель преломления равен отношению скоростей светового колебания в одной и другой среде. Также можно найти и угол, на который отклоняется свет.

Это интересно! Изучаем термины: энтропия – что же это такое простыми словами

Видео

В интернете можно найти видео, демонстрирующие, как работает принцип Гюйгенса-Френеля. Например, наглядная демонстрация для отражения плоской волны от поверхности доказывает, что угол падения и угол отражения равны.

Если волна падает на плоскость, отражаясь от нее, различные точки волновой поверхности доходят до плоскости неодновременно. Начинают распространяться вторичные колебания.

Касательная к ним — это и есть волновой фронт отраженного колебания. Решив простую геометрическую задачу о равенстве треугольников, можно установить, что углы, под которыми излучение падает и отражается, равны.

Можно построить изображение источника в плоском зеркале. Фронт отраженного возмущения будет сферой с центром в некоторой точке. Эта точка и будет мнимым изображением плоского источника в зеркале.

Можно найти видео, иллюстрирующие и другие физические явления. Например, можно пронаблюдать зоны Френеля для электромагнитного колебания. Также можно найти лекции, посвященные принципу Гюйгенса-Френеля и другим вопросам оптики.

Это интересно! Формулировки законов Исаака Ньютона: кратко и понятно

Полезное видео

Заключение

Принцип Гюйгенса-Френеля дает возможность объяснить такие оптические явления, как рефракцию, дифракцию, распространение света по прямой, интерференцию. С его помощью можно приближенно решать задачи оптики, которые очень трудно решить точными методами. Это утверждение — основной постулат волновой теории и применимо не только к распространению светового излучения, но и к другим волновым процессам.

Источник

Зоны Френеля. Просто о сложном.

Научиться настройке MikroTik можно на онлайн курсе по оборудованию этого производителя. Автор курса является сертифицированным тренером MikroTik. Подробней Вы можете прочитать в конце статьи.

Зоны Френеля используются теорией распространения для расчета отражений и дифракционных потерь между передатчиком и приемником. Зоны Френеля нумеруются и называются «F1», «F2», «F3» и т. д.

Существует бесконечное количество зон Френеля, однако только первые 3 имеют реальное влияние на распространение радиоволн.

Что такое зона Френеля и почему это важно?

Зона Френеля — это цилиндрический эллипс, проведенный между передатчиком и приемником. Размер эллипса определяется частотой работы и расстоянием между двумя участками.

Определяем размер зоны

Когда радиосигнал проходит между передатчиком и приемником, он может распространяться несколькими путями. Он может идти напрямую между передатчиком и приемником (основной сигнал). Сигнал может отражаться от земли и затем переноситься на удаленный приемник (отраженный сигнал). Он может идти влево или вправо и отражаться от «холма» (еще один отраженный сигнал).

Радиус зоны Френеля описывает это отражение относительно общей длины радиотрассы. Рисунок выше показывает основные и отраженные сигналы и F1 (первая зона Френеля) и F2 (вторая зона Френеля). Отражение может происходить в любом месте между передатчиком и приемником. На рисунке показано отражение, происходящее в случайном месте, а не в центре пути.

Когда сигнал отражается, происходят две вещи:

ВАЖНО! На длинном пути сдвиг может составить 180º или больше.

Почему это важно? Приемная антенна не может различить основной и отраженный сигналы. Они оба на одной частоте. Он принимает как основной, так и отраженный сигналы. Он также получает любые другие сигналы в пределах своего заданного диапазона частот.

Когда антенна получает основной сигнал и отраженный сигнал, эти два сигнала будут объединяться и суммироваться на антенне. Если они сдвинуты на 360º (по фазе), это не проблема. Однако, если сигналы разнесены на 180º (противоположная фаза), они будут взаимно поглощаться, и приемник ничего не получит.

Метод зон Френеля

Для нахождения результата интерференции вторичных волн Френель предложил метод разбиения волнового фронта на зоны, называемые зонами Френеля.

Зона Френеля 1 (F1)

Радиус первой зоны Френеля рассчитывается так, чтобы разница в длине пути между основным сигналом и отраженным сигналом от расстояния радиуса F1 составляла 180º. Отраженный сигнал, смещенный на 180º расстояния пути плюс 180º от фактической точки отражения, составляет 360º фазового сдвига. Два сигнала, основной и отраженный, поступают на антенну на 360º друг от друга или в фазе. Они будут складываться и не влияют на производительность приемника.

Этот сдвиг фазы отражения может происходить в любом месте от вычисленной «трубки» зоны Френеля, известной как эллипс.

Зона Френеля 2 (F2)

Радиус второй зоны Френеля рассчитывается так, чтобы разница в длине пути между основным и отраженным сигналами от второй трубки зоны Френеля составляла 360º.

Это очень важно, так как отраженный сигнал имеет автоматический фазовый сдвиг на 180º плюс разница в длине пути 360º равна сдвигу фазы 540º. 540º и 180º имеют одинаковый фазовый сдвиг в математической модели, и два сигнала будут отменены, не оставляя сигнала на приемнике.

Вторая зона Френеля, F2, является зоной отражения, которая не учитывается при проектировании радиотрассы.

Зона Френеля 3 (F3)

Третья зона Френеля имеет разницу в длине пути 540º. Добавьте это к сдвигу отражения 180º; общее количество составляет 720º, и 2 сигнала находятся в фазе.

Эффект зоны Френеля

Конечным результатом является то, что четные зоны Френеля отражают сигнал 180 градусов. Это вредно для распространения по радио. Зоны Френеля с нечетным номером имеют фазовый сдвиг на 360º и не имеют никакого эффекта. Нечетные зоны Френеля — это «хорошие парни».

Эффект этих отражений в мобильной работе может ощущаться, например, вблизи крайнего конца ретранслятора.

В приемнике слышно быстрое увеличение / уменьшение сигнала, которое часто называют «пикетным ограждением».Быстрое увеличение и уменьшение сигнала от движущегося радио или транспортного средства называется замиранием Рэлея. Это является прямым результатом появления и исчезновения отражений в зоне Френеля, когда транспортное средство движется по шоссе.

Радиотерминалы «точка-точка»

Радиосвязи точка-точка обсуждаются далее в этой статье, однако стоит отметить одну хитрость при проектировании линий связи точка-точка.

Поскольку зона F2 вредна для уровня принимаемого сигнала, высоту антенны часто выбирают таким образом, чтобы F1 была беспрепятственной траекторией, а F2 препятствовала возвышению или утолщению земли вдоль трассы.

Любые 180º отраженные сигналы вдоль зоны F2 ослабляются холмом или землей и не достигают приемной антенны, чтобы создавать помехи и подавлять основной приемный сигнал.

Радиус зоны Френеля и расстояние до Земли

Диаметр зоны Френеля (половина диаметра — это радиус) эллиптического цилиндра можно рассчитать. Важным компонентом радиуса зоны Френеля является зазор между цилиндром зоны Френеля и поверхностью земли. Как показано на рисунке 2, показаны радиус зоны Френеля и расстояние от нижней части зоны Френеля до Земли.

При превышении 60% радиоканал считается «чистым, прямой видимости» и не несет дифракционных потерь.

Это понимание зон Френеля и их влияния помогает понять, как и почему радиопокрытие может быть предсказано с использованием математики, а теперь и компьютеров.

Дифракция Френеля на круглом отверстии

Предположим, что монохроматический луч света падает на экран с круглым отверстием в нем. На определенном расстоянии от отверстия на втором экране можно наблюдать дифракционную картину. Структура рисунка зависит от длины волны, и распределение фаз входящего волнового фронта, а также по диаметру, отверстия и расстояния, от дыры до экрана.

В этом так называемом дифракционном режиме ближнего поля или Френеля монохроматическая плоская или сферическая волна, которая освещает отверстие, будет создавать дифракционную картину в виде набора концентрических колец. Излучение на оптической оси будет минимальным или максимальным, когда при постоянной длине волны и диаметре отверстия расстояние от отверстия до экрана наблюдения уменьшается от бесконечности до нуля.

Кольца появляются после прохождения критического расстояния (также называемого длиной Рэлея):

\( z_p = A \lambda Z_p = A \lambda \)

Если ​ \( r > 3pZ>Z_p \) ​ z > z R «>— колец нет, но наблюдается плавное распределение освещенности в виде квадрата функции Бесселя, форма которого (но не диаметр пучка) остается постоянной при увеличении z. Это дальнее поле также называется дифракцией Фраунгофера.

То, появляется ли максимум или минимум на оптической оси, можно понять с помощью теории зон Френеля. Если число полу-лямбда-зон, «видимых» наблюдателем, нечетно, наблюдается максимум, четное количество зон создает минимальное излучение. Количество зон Френеля указывается номером Френеля:

В этих экспериментах измеряются расстояния, на которых появляются максимальная или минимальная интенсивность на оптической оси. Из этих измерений можно определить длину волны света, если известен диаметр отверстия.

В этом упражнении рассматриваются два входящих волновых фронта: плоская волна и сферическая волна.

Дифракция Френеля на маленьком круглом экране

Сферическая волна, распространяющаяся из точечного источника, встречает на своем пути экран с круглым отверстием

Каковы условия для дифракции Френеля?

Дифракция Френеля возникает, когда либо расстояние от источника до препятствия, либо расстояние от препятствия до экрана сравнимо с размером препятствия. Эти сопоставимые расстояния и размеры приводят к уникальному дифракционному поведению.

Почему дифракция Френеля отличается от других видов дифракции?

Как дифракция Френеля решается математически?

Принцип Гюйгенса — Френеля

Принцип Гюйгенса-Френеля гласит, что каждая точка на волновом фронте является источником вейвлетов. Эти вейвлеты распространяются в прямом направлении с той же скоростью, что и исходная волна. Новый волновой фронт — это линия, касающаяся всех вейвлетов.

Рис 3. Форма волны

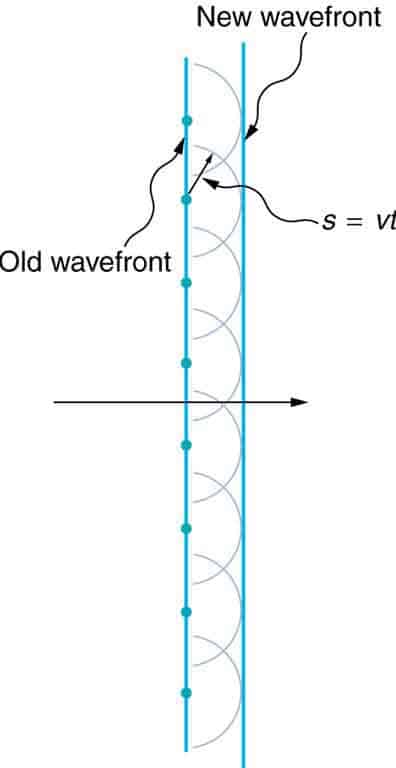
Кристиан Гюйгенс был голландским ученым, который разработал полезную технику для определения того, как и где распространяются волны. В 1678 году он предположил, что каждая точка, к которой относится световое возмущение, сама становится источником сферической волны. Сумма вторичных волн (волн, являющихся результатом возмущения) определяет форму новой волны, показывает вторичные волны, идущие вперед от их источника. Он смог придумать объяснение линейного и сферического распространения волн и вывести законы отражения и преломления (описанные в предыдущих атомах), используя этот принцип. Однако он не мог объяснить то, что обычно называют дифракционными эффектами. Эффекты дифракции — это отклонения от прямолинейного распространения, которое возникает, когда свет сталкивается с краями, экранами и отверстиями.

Прямой волновой фронт: принцип Гюйгенса, применяемый к прямому волновому фронту. Каждая точка на фронте волны излучает полукруглый вейвлет, который перемещается на расстояние:

Новый волновой фронт представляет собой линию, касательную к вейвлетам.

Принцип Гюйгенса

На рисунке показан простой пример дифракционного принципа Гюйгенса. Принцип может быть показан с помощью уравнения ниже:

где s — расстояние, V — скорость распространения, а t — время.

Каждая точка на волновом фронте испускает волну со скоростью V. Испускаемые волны полукруглые и появляются в момент времени t. Новый волновой фронт касается вейвлетов. Этот принцип работает для всех типов волн, а не только для световых волн. Принцип полезен при описании отражения, преломления и интерференции. наглядно показывает, как принцип Гюйгенса может быть использован для объяснения отражения, и показывает, как его можно применять к преломлению.

Рефракция Гюйгенса: принцип Гюйгенса применяется к прямому волновому фронту, перемещающемуся из одной среды в другую, где его скорость меньше. Луч изгибается в направлении перпендикуляра, поскольку вейвлеты имеют меньшую скорость во второй среде.

Отражение : принцип Гюйгенса применяется к прямому волновому фронту, ударяющемуся о зеркало. Показанные вейвлеты испускались, когда каждая точка на фронте волны ударялась о зеркало. Касательная к этим вейвлетам показывает, что новый волновой фронт был отражен под углом, равным углу падения. Направление распространения перпендикулярно фронту волны, как показано стрелками, направленными вниз.

Пятно Пуассона

Пятно Пуассона является доказательством того, что даже если вы правы, вы можете быть не правы. Узнайте, почему эта концепция физики привела к тому, что имя Симеона Пуассона прожило в позоре почти 200 лет.

В начале восемнадцатого столетия Французская академия решила провести товарищеский конкурс. Члены Академии, как и ученые всего мира, заметили, что когда свет перемещался из одной среды в другую, он изгибался. Стекло, вода, гель, все, что позволяет свету проходить через него, даст ему проход, только если он изменит свой ход. Люди могли измерить изгиб света, но были озадачены тем, что заставило это произойти. Французская академия пыталась решить эту проблему, противопоставляя умы разных ученых.

Помните Августина Френеля? Он был инженером и изучал эффекты света. Работая оттуда, он придумал новую идею; свет излучался волнами, перпендикулярными направлению, в котором он проходил. Его идея вызвала волнение, особенно у пуассоновских пэров. Они полагали, что свет путешествовал как ряд частиц, все из которых имели сложные взаимодействия друг с другом. Пуассон, Френель и другие ученые собрались вместе и провели волнующую серию дискуссий о природе света и наблюдаемых эффектах его путешествия через различные среды.

К концу дебатов Пуассон выдвинул аргумент, который, казалось, сжег теорию Френеля до основания и «засолил землю под ней». Если кого-то забрасывают предметами, его лучший шанс избежать травмы — спрятаться за более крупным предметом (по крайней мере, пока ракеты, ищущие тепло, не разрушат его для всех). Спрячьтесь за скалой, и поток гальки отскочит от скалы и пролетит мимо, не задев вас. Если, с другой стороны, человек по пояс в воде и хочет спрятаться от волны, он не будет в безопасности, приседая за скалой. Волны огибают твердые предметы.

Пуассон рассуждал, что если свет действительно был волной, то когда свет включался на совершенно сферическом объекте, световые волны могли бы огибать этот объект. Идеальная симметрия сферы означала, что все световые волны встретятся в точном центре тени позади нее, ведь там люди смогут увидеть яркое пятно света.

Это было нелепо. После выступления, как все закончили смеяться, успешные французские ученые пошли развлечься или выпить что-нибудь в близлежащем заведении. По крайней мере, один человек не присоединился к ним. Доминик Араго, один из судей, понял, что Пуассон описал идеальный эксперимент. Он нашел круглый предмет, он нашел свет, и довольно скоро он нашел это пятно. Что явилось подтверждением словам Пуассона.

Ничего не оставалось, кроме как вручить приз Френелю. Пуассон выдвинул следствие света как волны, которая была настолько нелепой, настолько маловероятной, что это не могло быть объяснено ничем другим. Френель был достаточно умен, чтобы выдвинуть теорию. Пуассон был достаточно умен, чтобы доказать, что Френель прав, и доказать, что он не прав. Несмотря на то, что Доминик Араго действительно прошел тест, крошечная точка света в центре тени сферического объекта всегда называлась Пятном Пуассона. В физике нет вечного движения, но есть постоянные насмешки.

MikroTik: куда нажать, чтобы заработало?
При всех своих достоинствах, есть у продукции компании MikroTik один минус – много разобщенной и далеко не всегда достоверной информации о ее настройке. Рекомендуем проверенный источник на русском языке, где все собрано, логично и структурировано – видеокурс «Настройка оборудования MikroTik». В курс входит 162 видеоурока, 45 лабораторных работ, вопросы для самопроверки и конспект. Все материалы остаются у вас бессрочно. Начало курса можно посмотреть бесплатно, оставив заявку на странице курса. Автор курса является сертифицированным тренером MikroTik.

Источник

5.2. Метод зон Френеля

Принцип Гюйгенса — Френеля в рамках волновой теории позволяет объяснить прямолинейное распространение света. Определим амплитуду световой волны в произвольной точке Р, используя метод зон Френеля. Рассмотрим сначала случай падающей плоской волны (рис. 5.2).

Пусть плоский фронт волны F, распространяющейся от расположенного в бесконечности источника света, в некоторый момент времени находится на расстоянии ОР – r₀ от точки наблюдения Р.

Рис. 5.2. Применение принципа Гюйгенса — Френеля к плоской волне: зоны Френеля на поверхности
плоского волнового фронта F представляют собой концентрические кольца
(для наглядности изображение зон Френеля развернуто на 90°, такими они выглядят из точки Р)

Все точки фронта волны, согласно принципу Гюйгенса — Френеля, испускают элементарные сферические волны, которые распространяются по всем направлениям и через некоторое время достигают точки наблюдения Р. Результирующая амплитуда колебаний в этой точке определяется векторной суммой амплитуд всех вторичных волн.

Колебания во всех точках волнового фронта F имеют одинаковое направление и происходят в одной фазе. С другой стороны, все точки фронта F находятся от точки Р на различных расстояниях. Для определения результирующей амплитуды всех вторичных волн в точке наблюдения Френель предложил метод разбиения волновой поверхности на кольцевые зоны, называемые зонами Френеля.

Взяв точку Р в качестве центра, построим ряд концентрических сфер, радиусы которых начинаются с и увеличиваются каждый раз на половину длины волны . При пересечении с плоским фронтом волны F эти сферы дадут концентрические окружности. Таким образом, на фронте волны появятся кольцевые зоны (зоны Френеля) с радиусами и т. д.

Для оценки амплитуд колебаний определим площади зон Френеля. Первая зона (круг):

вторая зона (кольцо):

третья и последующие зоны (кольца):

Таким образом, площади зон Френеля примерно одинаковы, поэтому, согласно принципу Гюйгенса — Френеля, каждая зона Френеля служит источником вторичных сферических волн, амплитуды которых приблизительно одинаковы. Кроме того, колебания, возбуждаемые в точке Р двумя соседними зонами, противоположны по фазе, так как разность хода соответствующих волн от этих зон до точки наблюдения Р равна . Поэтому при наложении эти колебания должны взаимно ослаблять друг друга, то есть амплитуда А результирующего колебания в точке Р может быть представлена в виде знакопеременного ряда

где А₁ — амплитуда колебаний в точке Р возбуждаемых действием центральной (первой) зоны Френеля, А₂ — амплитуда колебаний, возбуждаемых второй зоной, и т. д.

Расстояние от m-й зоны до точки Р медленно растет с номером зоны m. Угол между нормалью к элементам зоны и направлением в точку Р также растет с m, следовательно, амплитуда А_m колебания, возбуждаемого m-й зоной в точке Р, монотонно убывает с ростом m. Другими словами, амплитуды колебаний, возбуждаемых в точке Р зонами Френеля, образуют монотонно убывающую последовательность:

Вследствие монотонного и медленного убывания А_т можно приближенно положить, что амплитуда колебаний от зоны с номером m равна среднему арифметическому амплитуд колебаний от двух соседних зон Френеля:

В выражении для амплитуды результирующего колебания все амплитуды от четных зон входят с одним знаком, а от нечетных — с другим. Запишем это выражение в следующем виде:

Выражения в скобках на основании (5.10) будут равны нулю, так что

Если же на пути волны поставить диафрагму с отверстием, оставляющим открытой только центральную (первую) зону Френеля, амплитуда в точке Р будет равна А₁, то есть в два раза превзойдет амплитуду, создаваемую всем волновым фронтом. Соответственно, интенсивность света в точке Р будет в четыре раза больше, чем при отсутствии преграды между источником света и точкой Р. Удивительно, не так ли? Но чудес в природе не бывает: в других точках экрана интенсивность света будет ослаблена, а средняя освещенность всего экрана при использовании диафрагмы, как и следовало ожидать, уменьшится.

Правомерность такого подхода, заключающегося в делении волнового фронта на зоны Френеля, подтверждена экспериментально. Колебания от четных и нечетных зон Френеля находятся в противофазе и, следовательно, взаимно ослабляют друг друга. Если поставить на пути световой волны пластинку, которая перекрывает все четные или нечетные зоны Френеля, то можно убедиться, что интенсивность света в точке Р резко возрастет. Такая пластинка, называемая зонной, действует подобно собирающей линзе. Подчеркнем еще раз: зоны Френеля — это мысленно выделенные участки поверхности волнового фронта, положение которых зависит от выбранной точки наблюдения Р. При другой точке наблюдения расположение зон Френеля будет иным. Метод зон Френеля — удобный способ решения задач о дифракции волн на тех или иных препятствиях.

Различают два вида дифракции. Если источник света S и точка наблюдения Р находятся далеко от препятствия, лучи, падающие на препятствие и идущие в точку Р, образуют практически параллельные пучки. В таком случае говорят о дифракции в параллельных лучах, или дифракции Фраунгофера. Если же рассматривается дифракционная картина на конечном расстоянии от препятствия, вызвавшего дифракцию, то говорят о дифракции сферических волн, или дифракции Френеля.

Источник