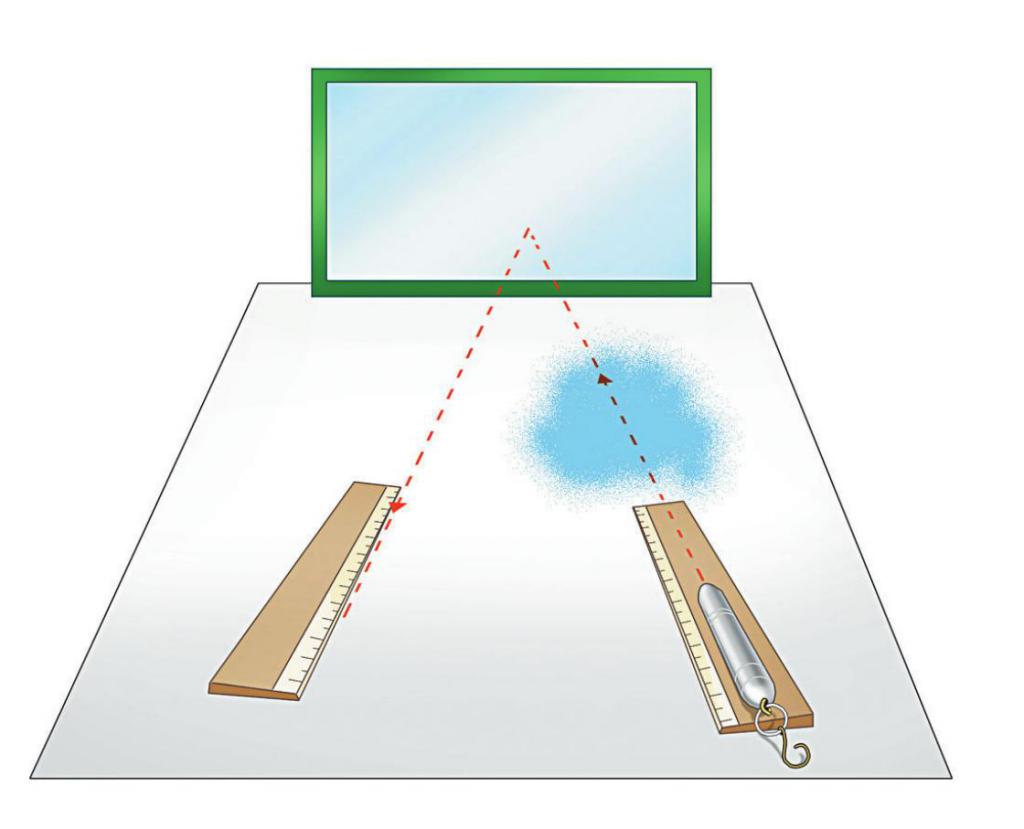
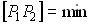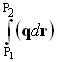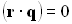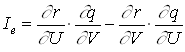в чем заключается принцип ферма

Принцип Ферма

Из Википедии — свободной энциклопедии

При́нцип Ферма́ (принцип наименьшего времени Ферма) — постулат в геометрической оптике, согласно которому свет выбирает из множества путей между двумя точками тот путь, который потребует наименьшего времени. То есть луч света движется из начальной точки в конечную точку по пути, минимизирующему время движения (или, что то же самое, минимизирующему оптическую длину пути). В более точной формулировке [1] : свет выбирает один путь из множества близлежащих, требующих почти одинакового времени для прохождения; другими словами, любое малое изменение этого пути не приводит в первом порядке к изменению времени прохождения.

Этот принцип, сформулированный в I в. Героном Александрийским для отражения света, в общем виде был сформулирован Пьером Ферма в 1662 году в качестве самого общего закона геометрической оптики. В разнообразных конкретных случаях из него следовали уже известные законы: прямолинейность луча света в однородной среде, законы отражения и преломления света на границе двух прозрачных сред.

Принцип Ферма представляет собой предельный случай принципа Гюйгенса — Френеля в волновой оптике для случая исчезающе малой длины волны света.

Принцип Ферма является одним из экстремальных принципов в физике.

Источник

Учебники

Журнал «Квант»

Общие

Кикоин А.К. Принцип Ферма //Квант. — 1984. — № 1. — С. 36-38.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Содержание

Основу геометрической оптики, которая оперирует понятием «световой луч», составляют три закона — законы прямолинейного распространения, отражения и преломления света. В давние времена, когда были сформулированы эти законы, вопрос о природе света еще не стоял, и за понятием «луч» не скрывалось ничего физически реального.

В 20-х годах XIX в. было выяснено, что свет — это волна. Луч света стал просто прямой, перпендикулярной волновой поверхности и указывающей направление распространения световой волны. На основе волновых представлений можно легко получить законы отражения и преломления света. Так это и сделано в учебнике «Физика 10» (§§ 37 и 65). Однако в конце XIX — начале XX вв. стало ясно, что свет обладает не только волновыми, но и корпускулярными свойствами тоже. С точки зрения корпускулярной (квантовой) природы свет представляет собой поток элементарных световых частиц — фотонов. В однородной среде луч можно считать траекторией движения фотонов.

Но интересно, что задолго до этого был сформулирован удивительный принцип, из которого прямо следуют все основные законы распространения света. Принцип этот, найденный французским математиком Пьером Ферма (1601-1665) около 1660 года, гласит: из всех возможных путей между двумя точками свет проходит по тому, по которому время прохождения наименьшее.

Из принципа Ферма (так его обычно называют) следует, что в однородной среде (в такой среде скорость света всюду одинакова) свет должен распространяться прямолинейно: прямая — кратчайшее расстояние между двумя точками, следовательно, и время распространения — наименьшее.

Покажем теперь, что закон отражения света — тоже прямое следствие принципа Ферма.

Закон отражения света

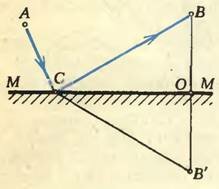
Пусть ММ — плоское зеркало. В точке А находится источник света, и нас интересует, по какому пути свет, отразившись от зеркала, приходит из точки А в точку В (рис. 1).

На рисунке 1 показаны некоторые из возможных путей — АА’В, АСВ, АВ’В. Таких «маршрутов» для света можно изобразить бесчисленное множество. Они различны по длине, так что на их прохождение требуется различное время. Оно зависит от того, в какую точку зеркала упадет луч и, отразившись, направится в В.

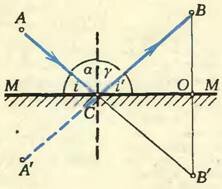
Из простых геометрических соображений легко выяснить, куда именно должен упасть луч, чтобы время его прохождения по «маршруту» точка А — зеркало — точка В было наименьшим. На рисунке 2 представлен один из возможных путей — АСВ.

Опустим из точки В перпендикуляр на зеркало ММ и продолжим его по другую сторону зеркала до точки В’, отстоящую от зеркала на расстоянии |ОВ’| = |ОВ|. Проведем линию СВ’. Получившиеся треугольники СОВ и СОВ’ равны друг другу, так как они прямоугольные, сторона ОС у них общая и |ОВ| = |ОВ’|. Следовательно, |CВ| = |CВ’|, откуда следует, что длина пути луча АСВ равна сумме длин от А до точки С падения луча на зеркало и от этой точки до токи В. Ясно, что эта сумма будет наименьшей, если точка С будет лежать на прямой, соединяющей точки А и В’ (рис. 3).

Тогда и сумма длин |АС| и |СВ|, то есть длина всего пути света, будет наименьшей, Наименьшим будет и время прохождения светом этого пути.

Закон этот, как мы видим, — следствие того, что свет как бы «выбирает» путь, который проходится за наименьшее время. Нетрудно видеть, что из принципа Ферма следует и утверждение, что луч падающий, луч отраженный и нормаль к зеркалу в точке падения лежат в одной плоскости. Если бы это было не так, то путь был бы длиннее и требовал бы большего времени.

Отметим еще одну важную особенность, связанную с отражением света от зеркала. Если в точке А (см. рис. 3) находится источник света, а в точке В — глаз, то глаз воспримет свет так, как будто бы источник света находится не в А, а в А’, а зеркала вовсе нет. Если зеркало убрать, а источник перенести из А в А’, то глаз не заметит такой замены.

Закон преломления света

Из принципа Ферма можно получить и закон преломления света (точнее — световых лучей). Здесь речь идет о переходе света из одной среды (среда I на рисунке 4) в другую (среда II) через границу раздела между ними. Различие сред состоит в том, что в них различны скорости распространения света.

Мы рассмотрим случай, когда среда I — это вакуум, в котором скорость света равна с, а вторая среда — какое-то прозрачное вещество (например, стекло, вода и т. д.), в котором скорость света υ меньше, чем с : с > υ.

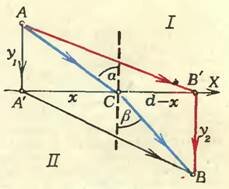
Между точками А в среде I и В в среде II также мыслимы бесчисленное множество путей, но, согласно принципу Ферма, свет «выбирает» тот из них, для прохождения которого нужно наименьшее время. Ясно, например, что путь АА’В не есть такой путь, потому что здесь свет проходит короткое (кратчайшее) расстояние в среде с большой скоростью и большое расстояние в среде с малой скоростью. Быть может, выгоднее путь АВ’В? Здесь свет в среде с малой скоростью проходит минимальную часть пути, а наибольшая часть приходится на среду с большой скоростью. Но есть ли именно этот путь самый выгодный в смысле экономии времени? Может быть, выгоднее несколько удлинить путь в среде II с тем, чтобы сократить путь в среде I? Словом, нужно найти, в какой точке свету (лучу) нужно пересечь границу раздела двух сред, чтобы время прохождения от А к В было наименьшим. Ясно, что эта точка лежит где-то между А’ и В’ (включая, возможно, и самую точку В’).

Обозначим расстояние между А’ и В’ через d. Если нужная нам точка С пересечения границы раздела находится на расстоянии х от А’, то от В’ она отстоит на расстоянии d — х (см. рис. 4). Путь АС, проходимый светом в среде I, равен \(

\sqrt\), а время прохождения этого пути

Путь СВ, проходимый светом в среде II, равен \(

Общее время t определяется равенством

Это приводит нас к такому условию для х:

Из рисунка 4 видно, что

где α — угол между падающим лучом и нормалью к границе раздела в точке падения (угол падения) и β — угол между этой нормалью и преломленным лучом (угол преломления). Условие (2) принимает поэтому вид:

В этом и заключается закон преломления для нашего случая: отношение синуса угла падения к синусу угла преломления равно отношению скоростей распространения света в вакууме и в среде, которая с ним граничит. Отношение \(

\frac<\upsilon>\) — величина постоянная, характерная для данной среды. Она называется показателем преломления вещества и обозначается буквой n, так что

В общем случае, когда свет переходит из произвольной среды, в которой скорость света равна υ₁, в среду со скоростью света в ней υ₂, закон преломления имеет вид

где n₂₁ — относительный показатель преломления сред 2 и 1.

Принцип Ферма справедлив, конечно, не только для тех простейших примеров отражения и преломления света, которые мы здесь рассмотрели. С помощью этого принципа можно понять и точно рассчитать ход лучей и в призме, и в линзе и в любой самой сложной системе призм, линз, зеркал.

Источник

Принцип Ферма

Луч света между двумя точками распространяется по тому пути, который занимает меньше всего времени.

Принцип Ферма, названный так по имени сформулировавшего его французского физика и математика Пьера Ферма (см. Великая теорема Ферма) является примером так называемого принципа экстремума. Принцип экстремума гласит, что любая система стремится к состоянию, при котором значение исследуемой величины принимает максимально или минимально возможное (т. н. экстремальное) значение. Вообще, принцип экстремума лежит в основе целого ряда законов геометрической оптики и распространения света. Что касается принципа Ферма, то он является простым математическим обобщением ранее сделанных наблюдений такого рода, и ранее открытые закон отражения света и закон Снеллиуса непосредственно вытекают из него. То есть, принцип Ферма можно считать теоретическим обобщением всех полученных к моменту его формулировки экспериментальных данных о поведении света.

Например, при попадании светового луча внутрь стеклянного параллелепипеда принцип Ферма подскажет нам, на какой угол преломится луч. Весь вопрос сведется к тому, по какому пути должен распространяться луч внутри стекла, чтобы на это ушел минимум времени, учитывая, что в стекле свет распространяется медленнее, чем в воздухе. Поскольку луч в стекле затормаживается, он неизбежно отклонится от направления, под которым он вошел в стекло, иначе возрастет время луча в пути. С другой стороны, если луч внутри стекла пойдет строго перпендикулярно к поверхности стекла, это приведет к увеличению общего пути, пройденного лучом, включая отрезки за пределами стекла, и, как следствие, также к увеличению затраченного времени. Следовательно, для нахождения кратчайшей по времени траектории пути луча между двумя точками нужно найти компромисс между увеличением совокупного пути луча и сокращением пути луча в тормозящей его среде.

При строгом геометрическом решении этой задачи (оно не столь сложно, сколь громоздко, поэтому приводить его здесь я не буду) мы получим закон Снеллиуса, описывающий преломление света. Применив же его к отраженному от поверхности лучу, мы без труда, чисто геометрически, получим закон отражения света, согласно которому угол падения равен углу отражения.

Иными словами, весь набор законов геометрической оптики выводится из принципа экстремума, согласно которому свет между двумя точками распространяется по пути, на преодоление которого у него уходит наименьшее время. Важно помнить и понимать, однако, что, подобно всем другим эмпирически выведенным законам природы, справедливость принципа Ферма полностью зависит от его экспериментальной проверки, однако данных, которые заставили бы в нем усомниться, на сегодняшний день не имеется.

Источник

В чем заключается принцип ферма

Все законы геометрической оптики следуют из закона сохранения энергии. Все эти законы не являются независимыми друг от друга.

4.3.1. Закон независимого распространения лучей

Если через точку пространства проходит несколько лучей, то каждый луч ведет себя так, как если бы других лучей не было.

Это справедливо для линейной оптики, где показатель преломления не зависит от амплитуды и интенсивности проходящего света.

4.3.2. Закон обратимости

Траектория и длина хода лучей не зависят от направления распространения.

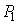
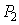
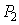
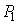
То есть, если луч, который распространяется от точки до точки , пустить в обратном ходе (от к ), то он будет иметь такую же траекторию, как и в прямом.

4.3.3. Закон прямолинейного распространения

4.3.4. Закон преломления и отражения

Закон отражения и преломления подробно рассматривается в Главе 3. В рамках геометрической оптики формулировки законов преломления и отражения сохраняются.

4.3.5. Принцип таутохронизма

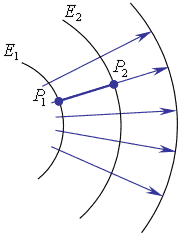
Рис.4.3.1. Принцип таутохронизма.

Рассмотрим распространение света, как распространение волновых фронтов (рис.4.3.1).

Оптическая длина любого луча между двумя волновыми фронтами одна и та же:

(4.3.1)

Волновые фронты – поверхности, которые оптически параллельны друг другу. Это справедливо и для распространения волновых фронтов в неоднородных средах

4.3.6. Принцип Ферма

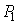
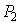
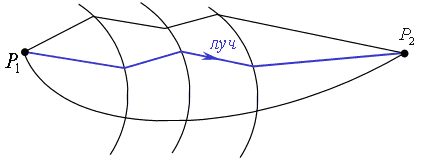
Пусть имеются две точки и , расположенные, возможно, в различных средах. Эти точки можно соединить между собой различными линиями. Среди этих линий будет только одна, которая будет являться оптическим лучом, который распространяется в соответствии с законами геометрической оптики (рис.4.3.2).

Рис.4.3.2. Принцип Ферма.

Можно сосчитать для сравнения оптическую длину этого луча и каких-либо других линий. В результате такого сравнения был получен принцип Ферма (Fermat principle).

Оптическая длина луча между двумя точками минимальна по сравнению со всеми другими линиями, соединяющими эти две точки:

(4.3.2)

Существует более полная формулировка:

Оптическая длина луча между двумя точками является стационарной по отношению к смещению этой линии.

Луч – кратчайшее расстояние между двумя точками. Если линия, вдоль которой мы измеряем расстояние между двумя точками, отличается от луча на величину 1-го порядка малости, то оптическая длина этой линии отличается от оптической длины луча на величину 2-го порядка малости.

Если оптическую длину луча, соединяющего две точки, поделить на скорость света, то получим время, необходимое на преодоление расстояния между двумя точками:

(4.3.3)

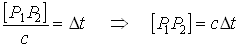
Еще одна формулировка принципа Ферма:

Луч, соединяющий две точки, идет по такому пути, который требует наименьшего времени (по самому быстрому пути).

Из этого принципа могут быть выведены законы преломления, отражения и т.д.

4.3.7 Закон Малюса-Дюпена

Нормальная конгруэнция сохраняет свойства нормальной конгруэнции в процессе прохождения через различные среды.

4.3.8 Инварианты

Инварианты (от слова неизменный) – это соотношения, выражения, которые сохраняют свой вид при изменении каких-либо условий, например, при прохождении света через различные среды или системы.

Интегральный инвариант Лагранжа

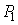
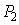
Пусть имеется некоторая нормальная конгруэнция (пучок лучей), и две произвольные точки в пространстве и (рис.4.3.4). Соединим эти две точки произвольной линией и найдем криволинейный интеграл.

(4.3.4)

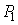Криволинейный интеграл (4.3.3), взятый между двумя любыми точками и 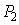, не зависит от пути интегрирования.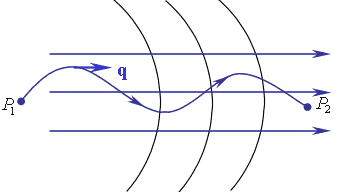

Рис.4.3.3. Интегральный инвариант Лагранжа.

Дифференциальный инвариант Лагранжа

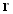
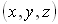
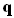
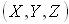
Луч в пространстве полностью описывается радиус-вектором , который содержит три линейные координаты , и оптическим вектором , который содержит три угловые координаты . Всего, таким образом, имеется 6 параметров для определения некоторого луча в пространстве. Однако из этих 6 параметров только 4 являются независимыми, так как можно получить два уравнения, которые связывают параметры луча друг с другом.

Первое уравнение определяется из длины оптического вектора:

(4.3.5)

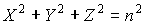
где 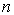– показатель преломления среды.

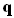
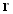
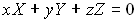
Второе уравнение вытекает из условия ортогональности векторов и :

(4.3.6)

Из выражений (4.3.5) и (4.3.6), воспользовавшись аналитической геометрией, можно вывести следующее соотношение:

(4.3.7)

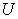где и 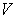– это пара любых из 6-ти параметров луча.

Дифференциальный инвариант Лагранжа:
Величина 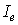сохраняет свое значение для данного луча при распространении пучка лучей через любую совокупность оптических сред.

Инвариант Штраубеля

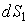
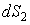
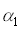
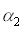
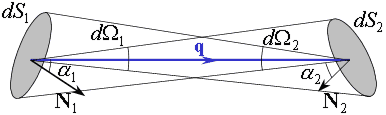
Рассмотрим в пространстве бесконечно малые площадки и , находящиеся на некотором расстоянии друг от друга (рис.4.3.4). Углы и – углы между нормалями к площадкам и направлением луча.

Рис.4.3.4. Световая трубка.

Геометрический фактор лучевой трубки записывается так:

(4.3.8)

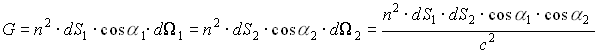
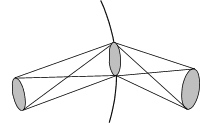
Рис.4.3.5. Инвариант Штраубеля.

Инвариант Штраубеля:
Геометрический фактор остается инвариантным при распространении лучевой трубки через любую последовательность различных сред (рис.4.3.5).

Инвариант Штраубеля выражает закон сохранения энергии, так как он показывает неизменность лучистого потока.

Из определения яркости (2.1.11) можно получить следующее равенство:

(4.3.9)
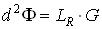
где 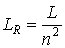– приведенная яркость, которая инвариантна, как уже было сказано в главе 2.

Источник

Что такое принцип Ферма?

Явления преломления и отражения

Под отражением понимают явление, при котором свет, распространяясь в прозрачном для него веществе, встречает на своем пути препятствие и резко изменяет свою траекторию. Препятствием может быть любое: жидкое или твердое тело, прозрачное и непрозрачное.

Явление отражения было известно с глубокой древности. Согласно историческим свидетельствам, законы отражения уже были сформулированы еще до нашей эры. А в первом веке нашей эры египетский философ Герон Александрийский высказал идею о траектории света, которую впоследствии использовал француз Пьер Ферма при формулировке своего принципа.

Явление преломления заключается в изломе прямой линии, по которой движется свет, при пересечении им поверхности, разделяющей два прозрачных материала. Заметим, что в случае отражения луч движется в одном прозрачном материале или, как принято говорить, в одной среде.

Законы распространения света в прозрачных средах

Перед тем как переходить к рассмотрению принципа Ферма, законы преломления и отражения света следует сформулировать. Для каждого из этих явлений принято выделять по два закона. Ниже они попарно объединены:

Формулировка принципа Ферма

Пьер Ферма был одним из известных математиков и юристов Франции в первой половине XVII века. Принцип, который носит его фамилию, он сформулировал в 1662 году, то есть спустя полвека после открытия Снеллом своего закона для преломления.

Кратко принцип Ферма может быть сформулирован так: свет при движении в абсолютно любых прозрачных средах выбирает такую траекторию, которую он пройдет за наименьшее время.

По сути, эта формулировка ничем не отличается от той, что сделал Герон Александрийский полторы тысячи лет ранее для явления отражения. Тем не менее француз сделал ее общей для всех явлений, связанных со светом, и показал, как из этого принципа могут быть получены законы преломления и отражения.

Вывод 1-го закона отражения

Пользуясь принципом Ферма, законы отражения получим математически. Для этого рассмотрим рисунок ниже.

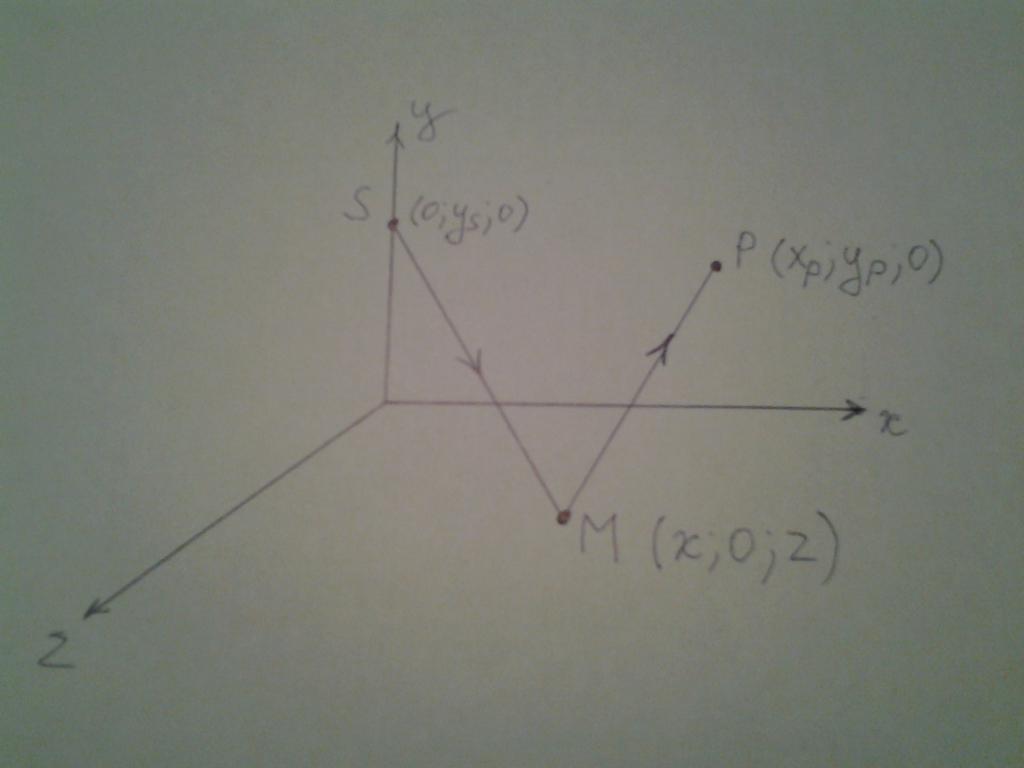
Здесь показано, что луч выходит с точки S, которая лежит на оси y. Затем он отражается от плоскости xz в некоторой неизвестной точке M. После отражения луч движется к точке P, лежащей на плоскости xy. Выбранное положение точек S и P не влияет на общность дальнейших рассуждений, а лишь упрощает математические выкладки.

Итак, запишем координаты каждой точки:

Координаты положения точек S и P известны. Задача состоит в том, чтобы найти такую точку M, которая будет соответствовать реальной траектории SMP, пройденной световым лучом. Также будем полагать, что рассматриваемое пространство является однородным, то есть скорость света в любой точке является постоянной величиной.

Согласно принципу Ферма, траекторию SMP свет пройдет за наименьшее время, если она будет наиболее короткой из всех возможных. Запишем ее длину:

Чтобы вычислить минимальную длину SMP, необходимо найти частные производные по x и z (неизвестные координаты точки M) и приравнять к нулю полученные результаты.

Сначала найдем частную производную по z. Имеем:

Это равенство имеет единственный корень, когда z = 0. Иными словами, точка M лежит на оси x, то есть в той же плоскости, что и точки P и S (плоскость xy). Откуда следует, что восстановленная нормаль к плоскости xz, в которой, по условию задачи, находится точка M, будет лежать вместе с SM и MP в одной плоскости (xy). Это и есть 1-й закон отражения.

Вывод 2-го закона отражения

Продолжим производить вычисления предыдущего пункта. Как было сказано, теперь необходимо найти частную производную по x. Имеем:

Последнее равенство запишем в виде:

Таким образом, следуя принципу Ферма, мы получили также 2-й закон отражения света.

Вывод закона преломления Снелла

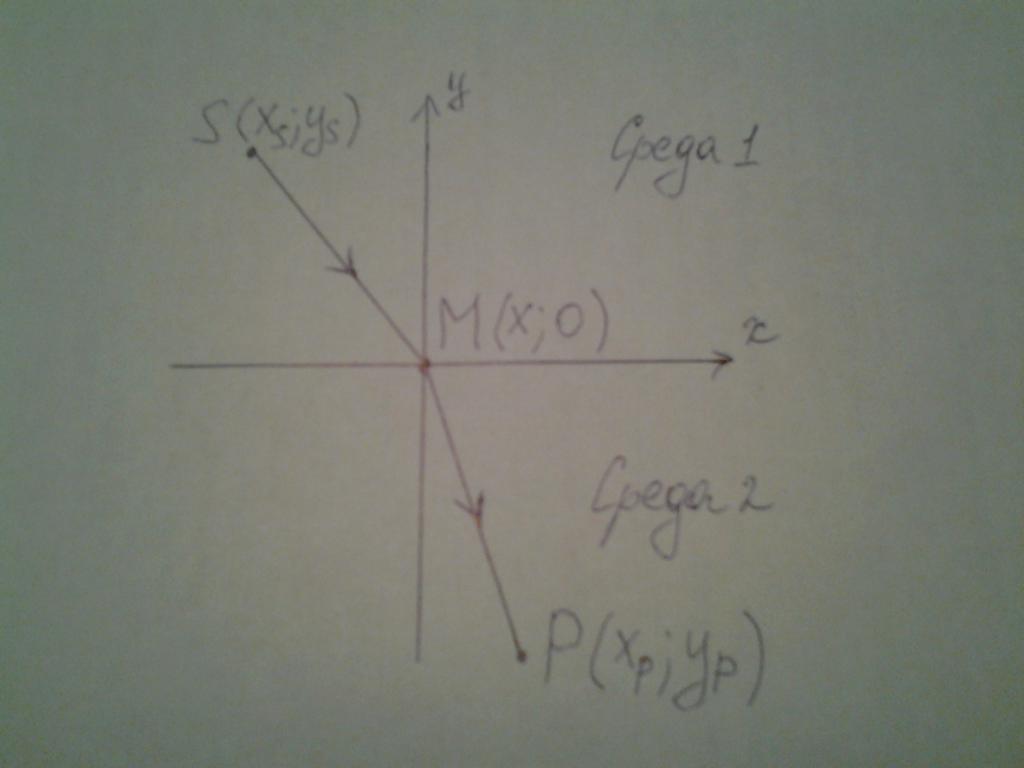
Теперь покажем, как можно вывести из принципа Ферма закон преломления света. Для этого рассмотрим рисунок, похожий на предыдущий.

Для простоты будем рассматривать случай в плоскости xy. Выпишем координаты источника S и приемника P света, которые находятся в разных средах:

Найдем неизвестную координату точки M. Координата y=0 для нее точно известна, поскольку именно на границе сред (ось x) меняется скорость распространения света. Длины отрезков SM и MP равны:

Общее время, которое затратит свет на прохождение траектории SMP, будет равно:

Используя функции синусов угла падения θ₁ и преломления θ₃, получаем:

Чтобы привести полученное равенство к закону Снелла в удобном виде (через показатели преломления сред), необходимо помножить левую и правую части на скорость света c.

Таким образом, применение принципа Ферма позволяет легко вывести законы для основных явлений движения светового луча в прозрачных материалах.

Движение света в неоднородной среде

Рассмотренные выше случаи предполагают, что материал является гомогенным, и световой луч при движении в нем скорость свою сохраняет. В случае же негомогенных сред справедливо равенство:

Отмеченный интеграл принято называть интегралом оптического пути. Принцип Ферма для оптического пути предполагает нахождение экстремумов для L.

Обобщенная формулировка рассматриваемого принципа

Принцип минимального времени для движения света является частным для более общей формулировки. В настоящее время обобщенный принцип Ферма формулируют так: свет выбирает во время движения такую траекторию, которая соответствует экстремумам оптического пути.

Экстремумами функции, согласно математическому определению, являются минимум, максимум и точка перегиба. Общий принцип Ферма удовлетворяет всем этим значениям, то есть траектория света не обязательно будет минимальной, она может быть и максимальной, и соответствующей точке перегиба оптического пути.

Бытовая аналогия с рассматриваемым принципом

Общий принцип Ферма, в свою очередь, является частным случаем так называемого принципа наименьшего действия. Здесь не будем приводить соответствующие определения и их математические формулировки, однако покажем, где можно применить предложенный французом принцип.

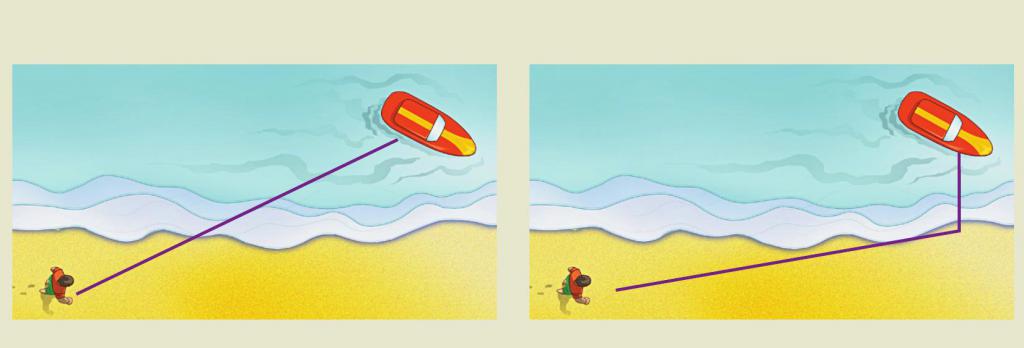
Используется он при решении простой, на первый взгляд, бытовой задачи: допустим, вблизи пляжа в море тонет человек. Как должен двигаться спасатель, находящийся на берегу, чтобы спасти утопающего? Конечно же, он должен прийти на помощь за наименьшее время. Поскольку скорость движения спасателя по пляжу больше, чем по воде, ему следует пробежать некоторое расстояние по берегу, а лишь затем прыгнуть в воду и поплыть. То есть задача сводится к применению принципа Ферма, где роль светового луча играет спасатель.

Отметим, что решение этой задачи не является простым, поскольку в его процессе появляются уравнения 4-й степени.

Источник