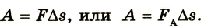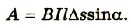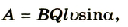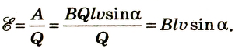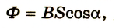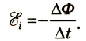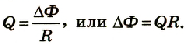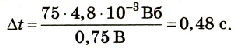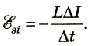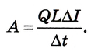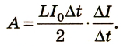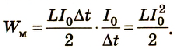в чем заключается правило ленца
Определение и объяснение правила Ленца
Правило Ленца позволяет определять направление индукционного тока в контуре. Оно гласит: «направление индукционного тока всегда таково, что его действие ослабляет действие причины, вызывающей этот индукционный ток».
Если траектория движущейся заряженной частицы изменяется каким бы то ни было образом в результате взаимодействия частицы с магнитным полем, то эти изменения приводят к возникновению нового магнитного поля, прямо противоположного тому магнитному полю, которое вызвало эти изменения.
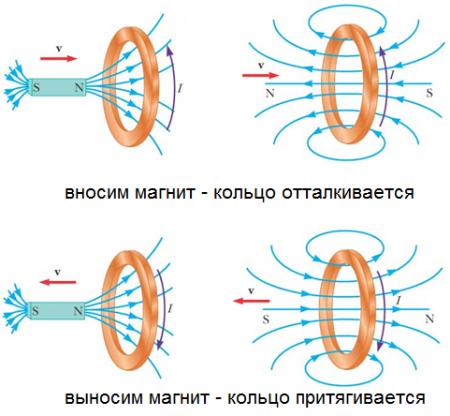
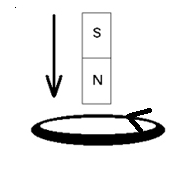
Например, если взять подвешенное на нити небольшое кольцо из меди, и попытаться внести в него северным полюсом достаточно сильный магнит, то по мере приближения магнита к кольцу, кольцо начнет отталкиваться от магнита.
Если проделать то же самое с разомкнутым кольцом, то кольцо реагировать на магнит не станет, хотя ЭДС в нем наведется, однако поскольку кольцо не замкнуто, индукционного тока не будет, а значит и направление его определять незачем.
Что на самом деле происходит здесь? Вдвигая магнит в целое кольцо — мы увеличиваем магнитный поток, пронизывающий замкнутый контур, и значит (поскольку согласно закону электромагнитной индукции Фарадея, генерируемая в кольце ЭДС пропорциональна скорости изменения магнитного потока) в кольце генерируется ЭДС.
А выдвигая магнит из кольца — мы тоже изменяем магнитный поток через кольцо, только теперь не увеличиваем его, а уменьшаем, и возникающая ЭДС снова будет пропорциональной скорости изменения магнитного потока, но направлена в противоположную сторону. Поскольку контур представляет собой замкнутое кольцо, то ЭДС конечно порождает в кольце замкнутый ток. А ток создает вокруг себя магнитное поле.
Направление линий индукции магнитного поля, порождаемого в кольце тока, можно определить по правилу буравчика, и они окажутся направлены именно так, чтобы препятствовать поведению линий индукции вносимого магнита: линии внешнего источника входят в кольцо, из кольца, соответственно, — выходят, линии внешнего источника покидают кольцо, в кольцо, соответственно, — направляются.
Правило Ленца в трансформаторе
Теперь вспомним как в соответствии с правилом Ленца ведет себя нагруженный сетевой трансформатор. Допустим, в первичной обмотке трансформатора ток нарастает, следовательно в сердечнике магнитное поле увеличивается. Увеличивается магнитный поток, пронизывающий вторичную обмотку трансформатора.
Поскольку вторичная обмотка трансформатора замкнута через нагрузку, то генерируемая в ней ЭДС породит индукционный ток, который создаст свое собственное магнитное поле вторичной обмотки. Направление этого магнитного поля будет таковым, чтобы ослаблять магнитное поле первичной обмотки. А значит ток в первичной обмотке будет увеличиваться (поскольку увеличение нагрузки во вторичной обмотке эквивалентно уменьшению индуктивности первичной обмотки трансформатора, а значит — понижению импеданса трансформатора для сети). И сеть станет совершать работу в первичной обмотке трансформатора, величина которой будет зависеть от нагрузки во вторичной обмотке.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Правило Ленца
теория по физике 🧲 магнетизм
Если присоединить катушку, в которой возникает индукционный ток, к гальванометру, можно обнаружить, что направление этого тока зависит от того, приближается ли магнит к катушке, или удаляется от нее. Причем возникающий индукционный ток взаимодействует с магнитом — притягивает или отталкивает его.
Катушка с протекающей по ней током подобна магниту с двумя полюсами — северным и южным. Направление индукционного тока определяет, какой конец катушки играет роль северного полюса, из которого выходят линии магнитной индукции. В каких случаях катушка будет притягивать магнит, а в каких отталкивать, можно предсказать, опираясь на закон сохранения энергии.
Взаимодействие индукционного тока с магнитом
Если магнит приближать к катушке, то в ней появится индукционный ток такого направления, что магнит обязательно отталкивается. Для сближения магнита и катушки при этом нужно совершить положительную работу. Катушка становится подобной магниту, обращенному одноименным полюсом к приближающемуся к ней магниту. Одноименные же полюсы отталкиваются. При удалении магнита, наоборот, в катушке возникает ток такого направления, чтобы появилась притягивающая магнит сила.
Представьте, что все было бы иначе. Тогда при введении магнита в катушку он сам бы устремлялся в нее. Это противоречит закону сохранения энергии, так как при этом увеличилась бы кинетическая энергия при одновременном возникновении индукционного тока, который также затрачивает часть энергии. Кинетическая энергия и энергия тока в этом случае возникали бы из ничего, без затрат энергии, что невозможно.
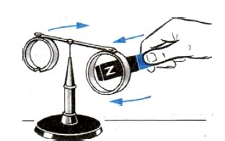
Справедливость вывода можно подтвердить с помощью следующего опыта. Пусть на свободно вращающемся стержне закреплены два алюминиевых кольца: с разрезом и без разреза. Если поднести магнит к кольцу без разреза, оно будет отталкиваться. Если поднести его к кольцу с разрезом, ничего не произойдет. Это связано с тем, что в нем не возникает индукционный ток. Этому препятствует разрез. Но если отдалять магнит от кольца без разреза, то оно начнет притягиваться.
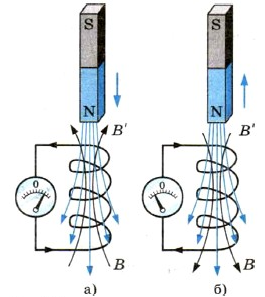
Опыты показывают, что притягивание или отталкивание кольца с индукционным током зависит от того, удаляется магнит, или притягивается. А различаются они характером изменения линий магнитной индукции, пронизывающих поверхность, ограниченную кольцом. В первом случае (рис. а) магнитный поток увеличивается, во втором (рис. б) — уменьшается. То же самое можно наблюдать в опытах с магнитом и проводящей катушкой.
Причем в первом случае линии индукции B’ магнитного поля, созданного возникшем в катушке индукционным током, выходят из верхнего конца катушки, та как катушка отталкивает магнит. Во втором же случае напротив, они входят в этот конец.
Правило Ленца
Описанные выше опыты позволяют делать вывод, что при увеличении магнитного потока через витки катушки индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует нарастанию магнитного потока через витки катушки. Если же магнитный поток через катушку ослабевает, то индукционный ток создает магнитное поле с такой индукцией, которая увеличивает магнитный поток через витки катушки.
Правило направления индукционного тока носит название правила Ленца.
Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван.
Применять правило Ленца для нахождения направления индукционного тока I i в контуре надо так:
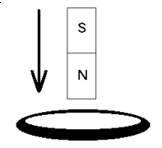
Пример №1. Найти направление индукционного тока, возникающего в кольце во время приближения к нему магнита (см. рисунок).
Линии магнитной индукции магнита обращены в сторону кольца, так как он направлен к нему северным полюсом. Так как магнит приближается к кольцу, магнитный поток увеличивается. Следовательно, кольцо отталкивается. Тогда оно обращено к магниту одноименным — северным — полюсом. Применим правило правой руки. Так как линии магнитной индукции выходят из северного полюса, направим к нему большой палец. Теперь четыре пальца руки покажут направление индукционного тока. В нашем случае он будет направлен против направления хода часовой стрелки.
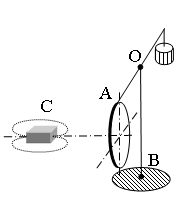

| МАГНИТ | ПОВОРОТ КОРОМЫСЛА И ТОК В КОЛЬЦЕ | ||
| А) | движется по направлению к кольцу, северный полюс обращён к кольцу | 1) | коромысло с кольцом поворачивается, отталкиваясь от магнита, ток идёт по часовой стрелке |
| Б) | движется к кольцу, к кольцу обращён южный полюс | 2) | коромысло с кольцом поворачивается, отталкиваясь от магнита, ток идёт против часовой стрелки |
| 3) | коромысло с кольцом поворачивается, притягиваясь к магниту, ток идёт по часовой стрелке | ||
| 4) | коромысло с кольцом поворачивается, притягиваясь к магниту, ток идёт против часовой стрелки |
Алгоритм решения
Решение
Запишем правило Ленца:
Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван.
Следовательно, если поднести к кольцу магнит северным полюсом, линии магнитной индукции поля, образованного магнитом, будут направлены в сторону кольца (т.к. они выходят из северного полюса). Тогда в кольце образуется такой ток, при котором с той стороны, с которой подносят магнит, тоже сформируется северный полюс. Используем правило правой руки и расположим большой палец правой руки так, чтобы он указывал в сторону северного полюса кольца с индукционным током. Тогда четыре пальца покажут направление этого тока. Следовательно, индукционный ток направлен по часовой стрелке.
Если поднести к кольцу магнит южным полюсом, линии магнитной индукции поля, образованного магнитом, будут направлены в сторону от кольца (т.к. они выходят из северного полюса). Тогда в кольце образуется такой ток, при котором с той стороны, с которой подносят магнит, тоже сформируется южный полюс. Используем правило правой руки и получим, что в этом случае индукционный ток будет направлен против часовой стрелки.
Так как магнит подносят к кольцу, а не отодвигают от него, то кольцо всегда будет отталкиваться, поскольку в нем возникают силы противодействия. Следовательно, позиции А соответствует строка 1, а позиции Б — строка 2.
pазбирался: Алиса Никитина | обсудить разбор | оценить
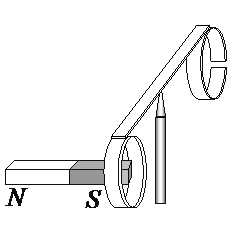
а) силы гравитационного взаимодействия между кольцом и магнитом
б) силы Ампера, действующей со стороны магнитного поля магнита на кольцо, по которому идёт индукционный ток
в) кулоновских (электростатических) сил, которые возникают при движении магнита относительно кольца
г) воздушных потоков, вызванных движением руки и магнита
Алгоритм решения
Решение
Гравитационные силы между магнитом и кольцом ничтожно малы при данных массах и расстояниях, поэтому они не могли вызвать притяжения кольца к магниту.
Кулоновские силы характеризуют силу электростатического взаимодействия зарядов. Поскольку магнит не имеет заряда, между ним и кольцом такие силы не возникают.
Металлическое кольцо достаточно тяжелое для того, чтобы заставить его стремительно двигаться вслед за магнитом.
Но вариант с силой Ампера подходит, так как сила Ампера — это сила, с которой действует магнитное поле на проводник с током. В момент, когда магнит двигают в стороны от кольца, магнитный поток, пронизывающий его, меняется. Это вызывает образование в кольце индукционного тока, который также порождает магнитное поле, противодействующее магнитному полю постоянного магнита.
pазбирался: Алиса Никитина | обсудить разбор | оценить
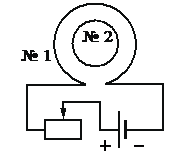
Из приведённого ниже списка выберите два правильных утверждения, характеризующих процессы в цепи и катушках при перемещении ползунка реостата вправо.
А) Сила тока в катушке № 1 увеличивается.
Б) Вектор индукции магнитного поля, созданного катушкой № 1, всюду увеличивается.
В) Магнитный поток, пронизывающий катушку № 2, увеличивается.
Г) Вектор индукции магнитного поля, созданного катушкой № 2, в центре этой катушки направлен от наблюдателя.
Д) В катушке № 2 индукционный ток направлен по часовой стрелке.
Алгоритм решения
Решение
Согласно утверждению А, при перемещении ползунка реостата вправо сила тока в катушке №1 увеличивается. Перемещая ползунок реостата вправо, мы увеличиваем сопротивление. Следовательно, сила тока уменьшается. Утверждение А — неверно.
Согласно утверждению Б, при перемещении ползунка реостата вправо вектор индукции магнитного поля, созданного катушкой №1, всюду увеличивается. Так как сила тока уменьшается, вектор индукции магнитного поля ослабевает. Утверждение Б — неверно.
Согласно утверждению В, при перемещении ползунка реостата вправо магнитный поток, пронизывающий катушку №2, увеличивается. Так как магнитное поле ослабевает, будет уменьшаться и магнитный поток, пронизывающий катушку № 2. Утверждение В — неверно.
Согласно утверждению Г, при перемещении ползунка реостата вправо вектор индукции магнитного поля, созданного катушкой №2, в центре этой катушки направлен от наблюдателя. В катушке №1 ток течёт по часовой стрелке, и по правилу буравчика эта катушка будет создавать магнитное поле, направленное от наблюдателя. В силу того, что сила тока в цепи уменьшается, будет уменьшаться и магнитный поток, пронизывающий вторую катушку. При этом согласно правилу Ленца во второй катушке будет создаваться индукционный ток, который направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван. В этом случае вектор индукции магнитного поля, созданного катушкой №2, в центре этой катушки сонаправлен с внешним полем и направлен от наблюдателя. Утверждение Г — верно.
Согласно утверждению Д, при перемещении ползунка реостата вправо в катушке №2 индукционный ток направлен по часовой стрелке. По правилу правой руки, индукционный ток в катушке 2 направлен по часовой стрелке. Утверждение Д — верно.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Электромагнитная индукция. Правило Ленца
Явление электромагнитной индукции заключается в том, что в результате изменения во времени магнитного потока, который пронизывает замкнутый проводящий контур, в контуре возникает электрический ток. Открыто это явление было физиком из Великобритании Максом Фарадеем в 1831 году.
Формула магнитного потока
Магнитный поток, который проходит через площадь замкнутого проводящего контура, можно задать следующей формулой:
Закон Фарадея
Закон Фарадея:
Правило Ленца
Согласно результатам опытов, индукционный ток, который возникает в замкнутом контуре в результате изменения магнитного потока, всегда направлен определенным образом. Создаваемое индукционным током магнитное поле препятствует изменению вызвавшего этот индукционный ток магнитного потока. Ленц сформулировал это правило в 1833 году.
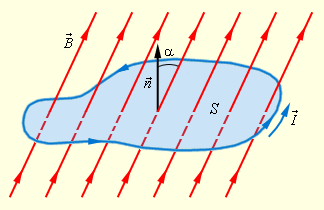
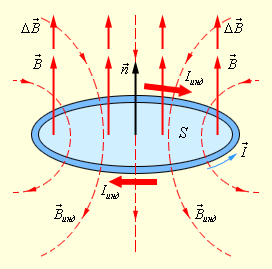
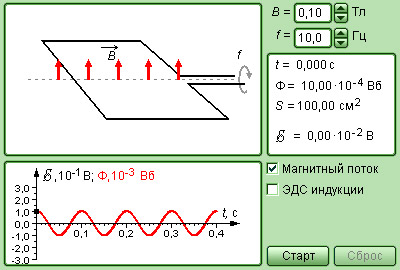
Проиллюстрируем правило Ленца рисунком, на котором изображен неподвижный замкнутый проводящий контур, помещенный в однородное магнитное поле. Модуль индукции увеличивается во времени.
Благодаря правилу Ленца мы можем обосновать тот факт, что в формуле электромагнитной индукции δ и н д и ∆ Φ ∆ t противоположны по знакам.
Если задуматься о физическом смысле правила Ленца, то это частный случай Закона сохранения энергии.
Причины возникновения индукционного тока в движущихся и неподвижных проводниках
Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:
Перейдем к рассмотрению этих случаев подробнее.
Перемещение контура или его частей в неизменном магнитном поле
При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δ и н д можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.
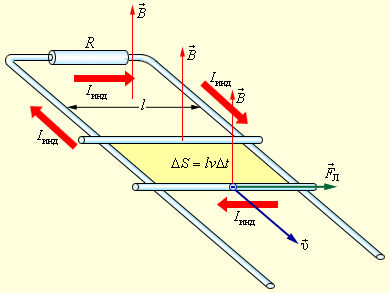
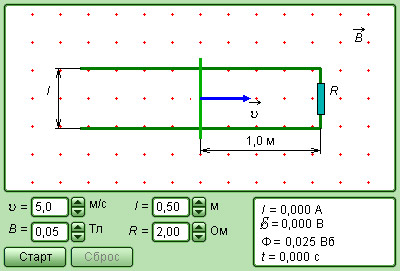
На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B → направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.
Работа силы F Л на пути l равна:
По определению ЭДС:
∆ Q = R I и н д 2 ∆ t = υ 2 B 2 l 2 R ∆ t
Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.
Изменение магнитного поля при неподвижном контуре
Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.
В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δ и н д в неподвижном проводнике.
В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δ и н д нельзя объяснить действием силы Лоренца.
Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.
Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δ и н д обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Содержание:
Электромагнитная индукция:
Обнаружение в 1820 г. датским физиком X. Эрстедом связи магнитного поля с электрическим током положило начало фундаментальным исследованиям открытого явления. Обладая широким научным кругозором, выдающийся физик и исследователь М. Фарадей предусмотрел возможность обратной связи магнитного поля и электрического тока, когда появление магнитного поля приводит к возникновению электрического тока. В результате длительных научных поисков он в 1821 г. получил первые положительные результаты: добился того, что в замкнутых проводниках, находящихся в переменном магнитном поле, возникал электрический ток. Явление получило название электромагнитной индукции, а ток, возникающий в проводниках, назвали индукционным.
Явление возникновения электрического тока в замкнутом проводнике, который расположен в переменном магнитов ном поле, называется электромагнитной индукцией.
Опишем основные опыты М. Фарадея, которые можно повторить и на школьном оборудовании.
C клеммами гальванометра соединим длинный проводник, пасть которого укреплена в штативе.
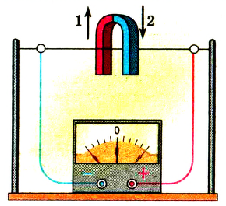
Постоянный подковообразный магнит сначала будем приближать к проводнику, а потом удалять от него (рис. 2.26). При этом увидим, что стрелка гальванометра будет отклоняться сначала в одну сторону, потом в противоположную.
Изменим условия опыта. Укрепим теперь подковообразный магнит в лапках штатива, а проводник, присоединенный к клеммам гальванометра, будем вводить в между полюсное пространство и выводить из него (рис. 2.27). Стрелка гальванометра также будет отклоняться сначала в одну, а потом в противоположную сторону. 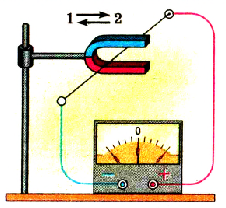
Pиc. 227. Опыт с движущимся проводником
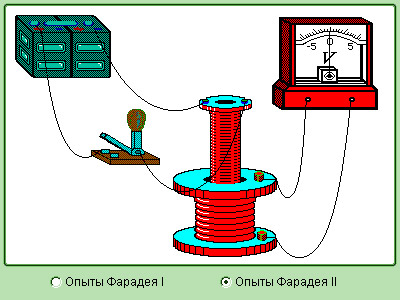
Видоизменим опыт. Одну из катушек присоединим к клеммам гальванометра, а вторую включим в электрическую цепь, состоящую из источника постоянного тока и выключатели. Замкнув цепь второй катушки, будем приближать ее к первой катушке (рис. 2.28). Отклонение стрелки гальванометра засвидетельствует появление тока в цепи первой катушки. Направление этого тока изменится, если вторую катушку удалять от первой. При неподвижных катушках ток будет отсутствовать.
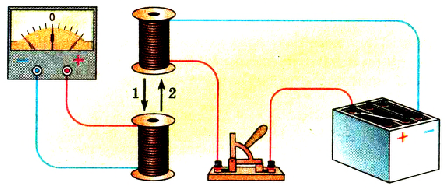
Рис. 228. Опыт с движущейся катушкой с током
Разместив вторую катушку неподвижно на первой, начнем замыкать и размыкать цепь второй катушки (рис. 2.29). Когда цепь будет замыкаться, стрелка гальванометра отклонится в одну сторону. При размыкании стрелка отклонится в противоположную сторону.
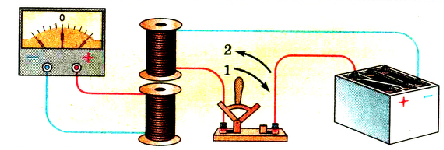
Pиc. 229. Замыкание и размыкание цепи второй катушки
Изменим условия последнего опыта. Включим в цепь второй катушки реостат и снова замкнем цепь. Когда стрелка остановится на нулевом делении, начнем изменять силу тока, перемещая ползунок реостата (рис. 2.30).
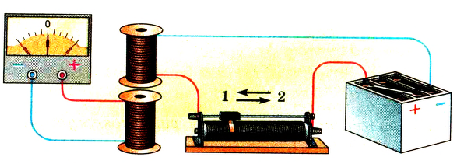
Рис. 230. Сила тока в катушке изменяется с помощью реостата
При увеличении силы тока в цепи первой катушки стрелка гальванометра будет отклоняться в одну сторону. При уменьшении силы тока отклонение стрелки будет противоположным.
После этого, не изменяя положения катушек и не разрывая цепи второй катушки, введем в катушки стальной стержень (рис. 2.31). Стрелка и в этом случае отклонится от положения равновесия и возвратится в начальное положение. Во время вынимания стержня из катушки заметим, что стрелка гальванометра отклоняется в противоположную сторону.
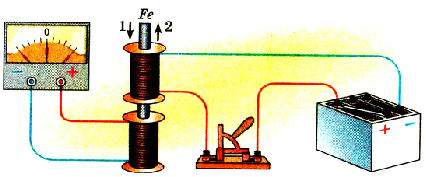
Pиc. 231. Опыт, когда движется стальной стержень
Электрический ток, возникающий в замкнутом проводнике в изменяющемся магнитном поле, называют индукционным.
На практике направление тока в проводнике, который возникает вследствие электромагнитной индукции, определяют по правилу правой руки (рис. 2.32): если правую руку разместить в поле так, чтобы линии магнитной индукции входили в ладонь, а отставленный большой палец показывал направление движения проводника, то вытянутые пальцы руки покажут направление тока в проводнике.
Рис. 2.32 Правило правой руки
Чтобы ток в проводниках протекал длительное время, необходимо, чтобы все это время существовала разность потенциалов. А это возможно при непрерывном движении проводника. При этом будет происходить разделе ние в проводнике положительно и отрицательно заряженных частиц под действием силы Лоренца, которая имеет неэлектростатическое происхождение. Это приводит к возникновению ЭДС индукции.
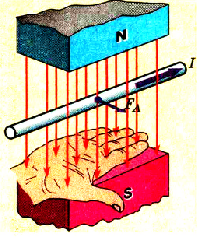
Определим способ рассчета ЭДС, для случая, когда прямой проводник, который является частью электрической цепи, равномерно движется в магнитном поле. Вызванное силой Лоренца движение заряженных частиц образует электрический ток, а в это время на него в магнитном поле будет действовать сила Ампера (рис. 2.33):
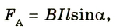
где В — модуль вектора магнитной индукции; I — сила тока в проводнике; l длина проводника; 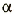
Возникающий ток в проводнике всегда будет иметь направление, при котором сила Ампера «тормозит» движение проводника. Чтобы проводник двигался равномерно (условие существования электрического тока), к нему нужно приложить силу, которая по модулю равна силе Ампера, а по направлению противоположна: 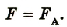
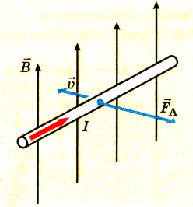
Рис. 2.33. К объяснению ЭДС индукции
Если за определенное время △t проводник сместится па △s, то работа будет равна
Приняв во внимание, что по определению сила тока равна 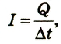
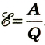
Таким образом, для случая, когда проводник движется равномерно в однородном магнитном поле, значение ЭДС индукции зависит от магнитной индукции поля, длины
прямого проводника и скорости его движения в магнитном поле, учитывая значение угла между 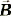
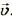
Правило Ленца
Правило установлено известным русским физиком Э.Х. Ленцем как обобщение многочисленных опытов по определению направления индукционного тока. C этой целью Э.Х. Ленц исследовал взаимодействие замкнутого проводника и переменного магнитного поля, которое вызвало индукционный ток в этом проводнике.
Чтобы лучше понять сущность этого правила, рассмотрим опыт.
На легком горизонтальном рычаге, который имеет вертикальную ось вращения, находятся два легких металлических кольца, одно из которых сплошное, я второе разрезано (рис. 2.35). Рычаг посажен на тонкое стальное острие так, чтобы трение было минимальным.
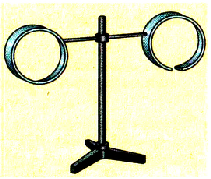
Pиc. 235. Прибор для демонстрации правила Ленца
Введем в сплошное кольцо катушку с ферромагнитным сердечником (электромагнитом), включенным в электрическую цепь из источника тока и выключателя (рис. 2.36).
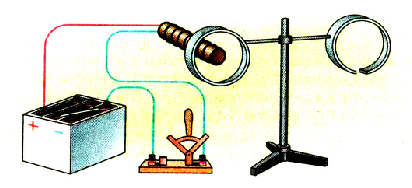
Рис. 236. К правилу Ленца
В момент появления тока в электромагните электропроводное кольцо, находящееся возле полюса электромагнита, всегда — притягивается к нему.
Если опыт повторить, изменив направление тока в катушке, то будем наблюдать тот же эффект. Таким образом, определяющим в данном случае является не направление магнитной индукции, а характер изменения магнитной индукции.
Если опыт попытаться пронести с разрезанным кольцом, то подобного эффекта наблюдать не сможем. Это свидетельствует, что отталкивание кольца связано с индукционным током, который возникает в сплошном кольце.
При размыкании цепи питания электромагнита проводящее кольцо будет двигаться от него.
Чтобы разобраться в дальнейших рассуждениях, необходимо вспомнить, что параллельные проводники, в которых ток проходит в одном направлении, притягиваются, а в противоположных отталкиваются. Таким образом, если кольцо отталкивается от катушки, то в нем индуцируется ток, противоположный току в катушке по направлению.
Взаимно противоположными будут и магнитные индукции полей этих токов.
Обобщив результаты опытов, можно сделать выводы, к которым пришел Э.Х. Ленц: магнитное поле индукционного тока всегда противодействует изменениям, которые вызвали этот так.
Правило Ленца: индукционный ток в замкнутом проводнике имеет такое направление, что его магнитное поле компенсирует изменение магнитного поля, которое вызвало этот ток.
Магнитный поток
Электромагнитную индукцию можно наблюдать в двух случаях: когда проводник движется в однородном магнитном поле или неподвижный проводник находится и магнитном поле, магнитная индукция которого изменяется со временем. Нa практике, как правило, случается так, что одновременно изменяется магнитная индукция и положение проводника в магнитном поле. Примером может быть движение проводника в неоднородном магнитном поле. Так как в этом случае расчеты сложнее» для их упрощения ввели физическую величину, которая одновременно зависит и от индукции магнитного поля, и от параметров движения проводника. Эта величина получила название магнитного потока.
Представим себе проводник в виде замкнутого кольца, которое находится в магнитном поле (рис. 2.38-а). Приведем кольцо в движение так, чтобы оно двигалось в плоскости, перпендикулярной к линиям магнитного поля. При этом количество линий индукции магнитного поля, которые проходят через него, будет уменьшаться, и в кольце возникнет индукционный ток (рис. 2.38-б).
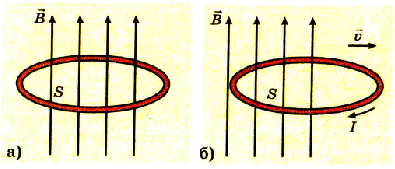
Pис. 238. Движение кольца в магнитом поле
Если теперь кольцо проводника поместить в магнитное поле, индукция которого изменяется, то количество линий магнитной индукции, которые проходят через контур, также будет изменяться и в проводнике возникнет индукционный ток (рис. 2.39). 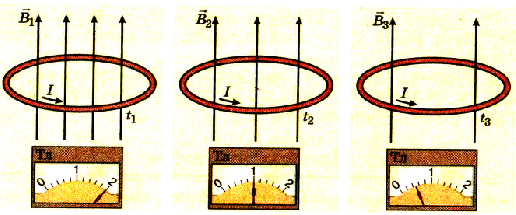
Pиc. 239. Изменение магнитного потока через кольцо
Оба описанных случая можно объяснить проще, если для каждого их них учитывать произведение площади кольца на значение магнитной индукции магнитного поля. Именно это произведение изменялось в обоих случаях. Фактически это произведение характеризовало поток линий магнитной индукции, которые пронизывают контур определенной площади, или просто — магнитный поток.
Магнитный поток Ф зависит не только от модуля магнитной индукции и площади контура, но и от угла, который образуют нормаль с плоскостью контура и вектором магнитной индукции поля (рис. 2.40). Поэтому в общем виде значении магнитного потока записывается как
Величина, которая описывает магнитное поле и равна произведению магнитной индукции на площадь замкнутого контура и косинус угла (между вектором магнитной индукции и нормалью к контуру), называется магнитным потоком, или потоком магнитной индукции.
Анализ формулы показывает, что минимальное значение магнитного потока (Ф = 0) будет тогда, когда 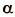
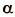
Любые изменения магнитного поля или площади контура вызывают явление электромагнитной индукции.
Таким образом, любое изменение магнитного потока обусловливает возникновение электрического тока в замкнутом проводящем контуре. C учетом закона Ома для полной цепи последний вывод можно записать так: любое, изменение. магнитного потока приводит к возникновению ЭДС индукции.
Закон электромагнитной индукции
Проанализировав результаты экспериментальных исследований электромагнитной индукции, можно найти общую формулу для выражения особенностей этого явления, которые отражают сущность закона электромагнитной индукции: при изменении магнитного потоки в замкнутых проводниках возникает электрический ток, вызванный ЭДС индукции, которая пропорциональна скорости изменения магнитного потока:
Закон электромагнитной индукции: электродвижущая сила индукции пропорциональна скорости изменения магнитного потока.
При использовании единиц СИ коэффициент k = 1. Приняв во внимание, что индукционный ток противодействует изменению магнитного потока (правило Ленца), окончательно имеем:
Так как согласно закону Ома 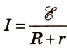
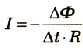
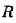
Заряд, который проходит в контуре вследствие электромагнитной индукции: Q = I∆t.
Учитывая, что заряд скалярная величина, а знак минус можно опустить, получим:
Пример решения задачи №1
Дано:
Φl= 4,8 • 10 3 Вб,
Ф2 = 0,
N= 75,
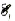
Общая ЭДС будет в N раз больше: 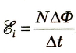
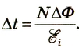
Подставив значения физических величин, получим
Ответ: ток исчезнет через 0,48 с.
Электродинамический микрофон
Одним из примеров практического применения явления электромагнитной индукции является электродинамический микрофон. C помощью этого прибора звуковые колебания превращаются в колебания электрического тока, которые усиливаются при помощи специальных электронных усилителей и используются в быту, научных исследованиях, производстве.
Микрофоны превращают звуковые колебания в электрические.
Обязательной частью электродинамического микрофона является постоянный магнит, изготовленный в виде кольца (рис. 2.41).
На стержне находится мембрана 3, которая колеблется под действием звуковых волн. К нижней части мембраны приклеена небольшая катушка 4 с некоторым количеством витков изолированного провода. Катушка помещена в кольцевую щель
между полюсами постоянного магнита.
В электродинамическом микрофоне катушка находится в магнитном поле.
Концы катушки соединены гибкими проводниками со специальными клеммами. Если на мембрану микрофона попадают звуковые волны, то она начинает колебаться вместе с катушкой. При колебании катушки магнитный поток, пронизывающий ее, изменяется и в ней индуцируется ЭДС индукции.
В движущейся катушке, находящейся в магнитном поле, возникает ЭДС индукции.
Если катушка включена в цепь электронного усилителя, то электрические колебания усиливаются и могут быть или записаны на магнитный либо оптический диск, или сразу
воспроизведены громкоговорителем.
Принцип действия электродинамического микрофона используется в различных датчиках для изучения и контроля колебательных процессов.
Самоиндукция
Каждый проводник, в котором существует электрический ток, создает «собственное» магнитное поле. Это поле образуется сразу же, как только в проводнике начинает про ходить электрический ток. Если индукция магнитного поля перед замыканием цепи была равна нулю, то через некоторое время после замыкания она будет иметь максимальное значение B, соответствующее силе тока в проводнике. Таким образом, момент возникновения электрического тока можно читать моментом начала изменения магнитного потока. А любое изменение магнитного потока, по закону электромагнитной индукции, порождает вихревое электрическое поле, способствующее появлению ЭДС индукции во всех проводниках,находящихся в магнитном поле.
Явление самоиндукции выявил Д. Генри в 1832 г.
Не может быть исключения и для проводника, который является «источником» этого поля. Вихревое поле создает и в нем ЭДС индукции 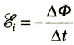
Наличие ЭДС самоиндукции можно подтвердить опытом. Для этого составим электрическую цепь из источника тока, выключателя и электрической лампочки (рис. 2.43). При
замыкании цепи лампочка зажигается практически мгновенно. Если же в цепь включить катушку с железным сердечником, то максимальная яркость свечения лампочки устанавливается постепенно (рис. 2.44).
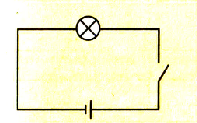 Pиc. 2.43. Лампочка загорается сразу после замыкания цепи | 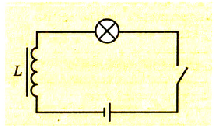 Рис 2.44 В цепи с катушкой лампочка загорается постепенно |
Это является свидетельством того, что ток в цепи увеличивается во мгновенно, а на протяжении некоторого времени. Посмотрев на графики рисунков 2.45 и 2.46, можно сказать, что в цепи, где находится катушка из 100 витков, ток нарастает быстрее, чем в цепи, в которой находится катушка из 1000 витков. На прохождение тока н цепи существенно влияет также ферромагнитный сердечник в катушке (рис. 2.47).
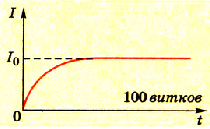 Pиc. 2.45. График силы тока при замыкании цепи с катушкой из 100 витков | 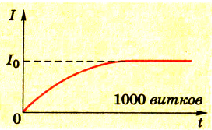 Рис. 2.46. График силы тока при замыкании цепи с катушкой из 1000 витков |
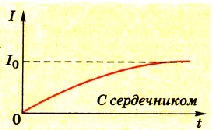 Рис. 2.47. График силы тока при замыкании цепи с катушкой (сердечником) |
Поскольку ЭДC самоиндукции противодействует ЭДС источники тока, то можно сделать вывод, что ЭДС самоиндукции зависит от характеристик катушки или проводника, включенного в электрическую цепь.
А магнитный поток, создаваемый катушкой или проводником, будет пропорционален силе тока в них: Ф
I. Если внести коэффициент пропорциональности, то можно получить более точное соотношение и новую формулу: Ф = L ∙ I. Здесь коэффициент пропорциональности L учитывает электромагнитные свойства катушки (проводника) и называется индуктивностью. Индуктивность определяется формой и размерами проводника, а также магнитными свойствами среды.
Физическую величину, которая характеризует электромагнитные свойства катушки или проводника, называют индуктивностью.
Если при изменении силы тока в проводнике на 1 А за 1 с в нем индуцируется ЭДС самоиндукции 1 В, то этот проводник имеет индуктивность 1 Гн.
В СИ индуктивность измеряют в генри (Гн) в честь известного американского физика Д. Генри.
Единица 1 генри имеет довольно большой размер, поэтому применяют, как правило, долевые единицы:
Если в любом проводнике изменяется электрический ток, то это приводит к изменению магнитного потока ΔΦ — LΔI, которое вызывает ЭДС самоиндукции:
Явление самоиндукции наблюдается также при размыкании цепи c током. Составим цепь из источника тока, выключателя, катушки и лампочки. Лампу накаливания, сопротивление которой значительно меньше сопротивления катушки, включим параллельно катушке (рис. 2.48). Если замкнуть цепь, то накаливание волоска лампочки будет происходить постепенно, как
бы с задержкой. Если после полного загорания лампы разомкнуть ключ, то она ярко вспыхнет. Это будет проявлением самоиндукции. В результате размыкания цепи возникнет ЭДС самоиндукции, которая поддержит ток в цепи лампочки и катушки.
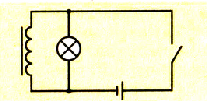
Рис. 2.48. Схема электрической цепи для наблюдения явления самоиндукции при размыкании
Пример решения задачи №2
Определить индуктивность катушки, если сила тока в ней изменяется на 50 А за 1 с и при этом появляется ЭДС самоиндукции 0,08 В.
Дано:
ΔI = 50 А,
Δt— 1 с,
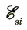
Ответ: индуктивность катушки 1,6 мГн.
Энергия магнитного поля
Самоиндукция подтверждает действие закона сохранения и превращения энергии в электромагнитных явлениях.
Как известно, вследствие явления самоиндукции при замыкании цепи возникает ЭДС самоиндукции 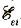
Любые изменения силы тока в катушке вызовут появление ЭДС индукции и приведут к выполнению работы источником тока для компенсации ее действия. Эта работа равна энергии магнитного поля катушки или проводника.
ЭДС самоиндукции зависит от индуктивности проводника и скорости изменения силы тока в нем.
При этом сила тока в цепи изменяется от пуля до Imax которое равно I0. По определению Q=IΔt.
Поскольку при замыкании цепи сила тока не имеет постоянного значения, то для упрощения расчетов будем считать,что сила тока линейно изменяется на протяжении всего времени. Тогда сила тока 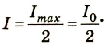
Таким образом,
Изменение силы тока ΔI за интервал времени Δt равно I0.
Работа, выполненная источником тока, равна энергии магнитного поля катушки с током:
Энергия магнитного поля катушки с током пропорциональна индуктивности катушки и квадрату силы тока в ней.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.