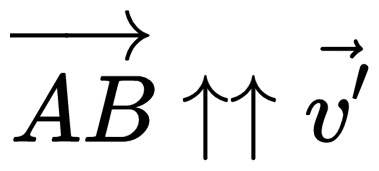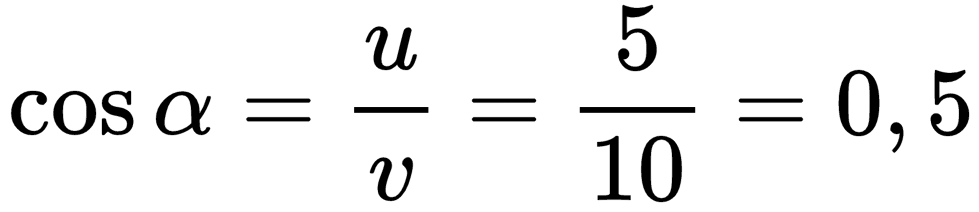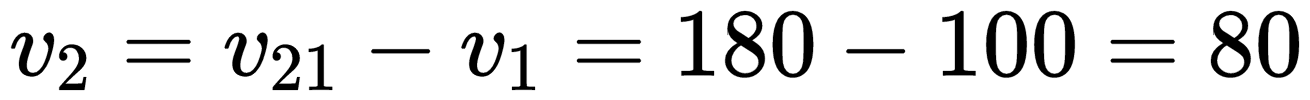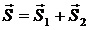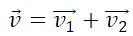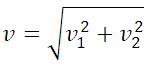в чем заключается относительность движения и покоя

Относительность механического движения

теория по физике 🧲 кинематика

Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.

Относительность перемещения

Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.

Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.

Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:

Относительность скорости в ПСО и НСО

Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.

Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.

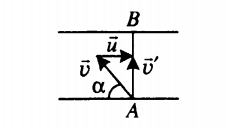
Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.

Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:

Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):

Косинусу 0,5 соответствует угол, равный 60 градусам.

Относительная скорость двух тел

Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.

Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:

v _отн — относительная скорость, или скорость первого тела относительно второго, v ₁ и v ₂ — скорость первого и второго тела относительно СО.

Варианты обозначения относительной скорости и их проекций:

Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.

Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.

Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:

Скорость второго автомобиля относительно дороги равна 80 км/час.

Правила сложения векторов

Сложение двух сонаправленных векторов
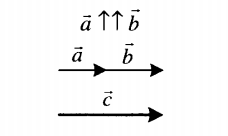	Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b.
Сложение двух противоположно направленных векторов
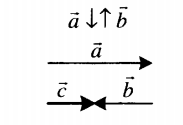	Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|.
Сложение двух векторов, расположенных друг к другу под углом
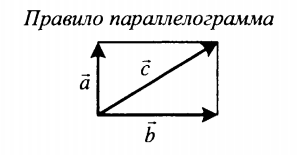
Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
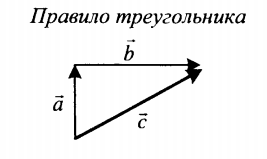	Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: .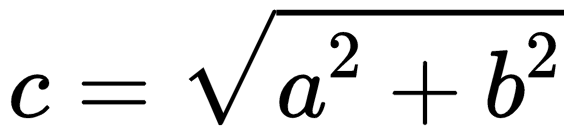
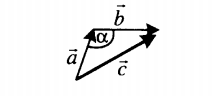	Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .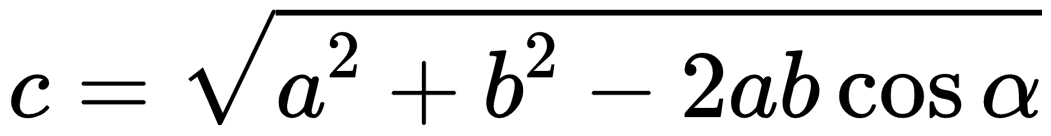
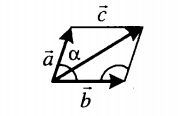	Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .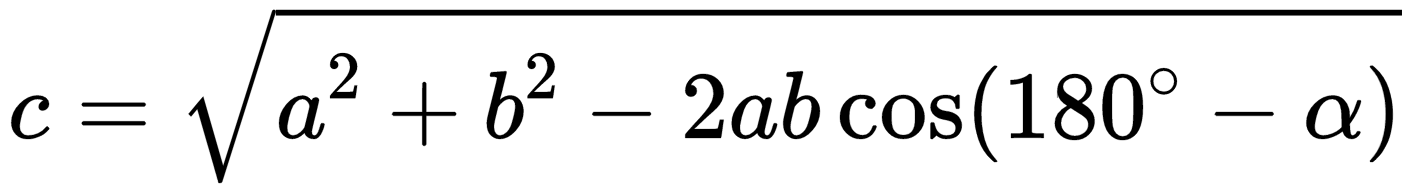

Правила вычитания векторов

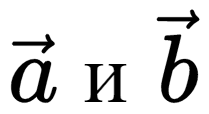
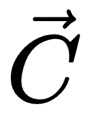
Эта таблица иллюстрирует правила вычитания векторов на примере векторов Результатом их вычитания является вектор .

Алгоритм решения

Решение

Записываем данные относительно Земли:

Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость второго автомобиля относительно оси ОХ ( v ₂), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v ₁).

Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость автомобиля относительно земли ( v ₁), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v ₂). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:

Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:

По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

В чем заключается относительность движения и покоя

Для изучения движения тел научимся прежде всего описывать движения. При этом вначале не будем выяснять, как возникают эти движения. Раздел механики, в котором движения изучаются без исследования причин, их вызывающих, называют кинематикой.

Движение каждого тела можно рассматривать по отношению к любым другим телам. По отношению к разным телам данное тело будет совершать различные движения: чемодан, лежащий на полке в вагоне идущего поезда, относительно вагона покоится, но относительно Земли движется. Воздушный шар, уносимый ветром, относительно Земли движется, но относительно воздуха покоится. Самолет, летящий в строю эскадрильи, относительно других самолетов строя покоится, но относительно Земли он движется с большой скоростью, например 800 километров в час, а относительно такого же встречного самолета он движется со скоростью 1600 километров в час.

В кинофильмах часто показывают одно и то же движение относительно разных тел: например, показывают поезд, движущийся на фоне пейзажа (движение относительно Земли), а затем — купе вагона, за окном которого видны мелькающие деревья (движение относительно вагона).

Всякое движение, а также покой тела (как частный случай движения) относительны. Отвечая на вопрос, покоится тело или движется и как именно движется, необходимо указать, относительно каких тел рассматривается движение данного тела. Иначе никакое высказывание о его движении не может иметь смысла.

Тела, относительно которых рассматривается данное движение, называют системой отсчета. Выбор системы отсчета при изучении данного движения делают в зависимости от условий задачи. Так, чтобы попасть во вражеский самолет с земной поверхности, нужно установить придел, исходя из скорости самолета в системе отсчета «Земля» (в нашем примере — 800 км/ч), а чтобы попасть в этот же самолет со встречного самолета, надо исходить из скорости цели в системе отсчета «встречный самолет» (1600 км/ч). При изучении движений на поверхности Земли обычно принимают за систему отсчета Землю (хотя, как сказано, можно выбрать за систему отсчета и поезд, и самолет, и любое другое тело). Изучая движение Земли в целом или движение планет, принимают за систему отсчета Солнце и звезды. Как увидим в гл. II, эта система особенно удобна при изучении законов динамики.

2.1. Будет ли развеваться флажок, укрепленный на корзине воздушного шара, уносимого ветром?

© 2021 Научная библиотека

Копирование информации со страницы разрешается только с указанием ссылки на данный сайт

Источник

Кинематика. Относительность движения.

Относительность механического движения заключается в относительности скоростей перемещения тел: их скорости будут различны относительно разных систем отсчета. Например, скорость человека, едущего в поезде, или летящего самолетом, будет отличаться как по величине, так и по направлению, в зависимости от того, в какой системе отсчета эти скорости определяются: в системе отсчета, связанной с движущимся транспортным средством, или с неподвижной Землей. Различными будут также траектории и скорости движения тела в разных системах отсчета. При механическом движении относительна также траектория движения.

Пройденный телом путь тоже зависит от системы отсчета. Рассмотрев тот же пример с пассажиром в поезде можно понять, что проделанный им путь относительно поезда за время поездки равен нулю (если он за все время не передвигался по вагону), или же намного меньше пути, который он преодолел вместе с поездом относительно Земли. Следовательно, при механическом движении относительным является и путь.

Любое движение, как и покой тела (как частный случай движения) относительны. Для ответа на вопрос, покоится тело или движется и как именно движется, необходимо указать, относительно каких тел рассматривается движение этого тела. В противном случае никакое высказывание о его движении не может иметь смысла.

Тела, относительно которых рассматривается данное движение, называют системой отсчета. Выбор системы отсчета зависит от условий задачи, тогда положение одного и того же тела можно одновременно рассматривать в разных системах координат. Следовательно, относительно разных тел отсчета в разных системах координат у одного и того же тела могут быть совершенно различные координаты. Это значит, что положение тела относительно: оно различно относительно разных тел отсчета и связанных с ними разных систем координат.

Но относительно не только положение тела. Относительно и его движение. В чем же относительность движения? Например, пилоту необходимо знать движение самолета относительно Земли и относительно воздуха, который в ненастную погоду сам движется; артиллеристу важно знать движение снаряда не только относительно Земли, на которой стоит орудие, но и относительно танка, в который он должен произвести выстрел, и который сам движется относительно Земли и т. д.

Движения одного и того же тела относительно разных тел отсчета, движущихся относительно друг друга, могут довольно сильно отличаться.

Источник

Как сказал.

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Я учу детей тому, как надо учиться

Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.

Урок 02. (дополнительный материал). Относительность механического движения

Относительность механического движения.

Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным.

Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляетсяотносительность механического движения.

Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Покой тоже относителен. Например, пассажир в покоящемся поезде смотрит на проходящий мимо поезд и не понимает, какой поезд движется, пока не посмотрит на небо или землю.

Все тела во Вселенной движутся, поэтому не существует тел, которые находятся в абсолютном покое. По той же причине определить движется тело или нет, можно только относительно какого-либо другого тела.

Например, автомобиль движется по дороге. Дорога находится на планете Земля. Дорога неподвижна. Поэтому можно измерить скорость автомобиля относительно неподвижной дороги. Но дорога неподвижна относительно Земли. Однако сама Земля вращается вокруг Солнца. Следовательно, дорога вместе с автомобилем также вращается вокруг Солнца. Следовательно, автомобиль совершает не только поступательное движение, но и вращательное (относительно Солнца). А вот относительно Земли автомобиль совершает только поступательное движение. В этом проявляется относительность механического движения.

Движение одного и того же тела может выглядеть по-разному с точки зрения различных наблюдателей. Скорость, направление движения и вид траектории тела будут различными для различных наблюдателей. Без указания тела отсчета разговор о движении является бессмысленным. Например, сидящий пассажир в поезде покоится относительно вагона, но движется вместе с вагоном относительно платформы вокзала.

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.

Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.

Галилей показал, что в условиях Земли практически справедлив закон инерции. Согласно этому закону действие на тело сил проявляется в изменениях скорости; для поддержания же движения с неизменной по величине и направлению скоростью не требуется присутствия сил. Системы отсчета, в которых выполняется закон инерции, стали называть инерциальные системы отсчета (ИСО).

Системы, которые вращаются или ускоряются, неинерциальные.

Землю нельзя считать вполне ИСО: она вращается, но для большинства наших целей системы отсчета, связанные с Землей, в достаточно хорошем приближении можно принять за инерциальные. Система отсчета, движущаяся равномерно и прямолинейно относительно ИСО, также инерциальная.

Г. Галилей и И. Ньютон глубоко осознавали то, что мы сегодня называем принципом относительности, согласно которому механические законы физики должны быть одинаковыми во всех ИСО при одинаковых начальных условиях.

Из этого следует: ни одна ИСО ничем не отличается от другой системы отсчета. Все ИСО эквивалентны с точки зрения механических явлений.

Принцип относительности Галилея исходит из некоторых допущений, которые опираются на наш повседневный опыт. В классической механике пространство и время считаются абсолютными. Предполагается, что длина тел одинакова в любой системе отсчета и что время в различных системах отсчета течет одинаково. Предполагается, что масса тела, а также все силы остаются неизменными при переходе из одной ИСО в другую.

В справедливости принципа относительности нас убеждает повседневный опыт, например в равномерно движущемся поезде или самолете тела движутся так же, как и на Земле.

Не существует эксперимента, с помощью которого можно было бы установить, какая система отсчета действительно покоится, а какая движется. Нет систем отсчета в состоянии абсолютного покоя.

Если на движущейся тележке подбросить монету вертикально вверх, то в системе отсчета, связанной с тележкой, будет изменяться только координата ОУ.

В системе отсчета, связанной с Землей, изменяются координаты ОУ и ОХ.

Следовательно, положение тел и их скорости в разных системах отсчета различны.

Рассмотрим движение одного и того же тела относительно двух разных систем отсчета: неподвижной и движущейся.

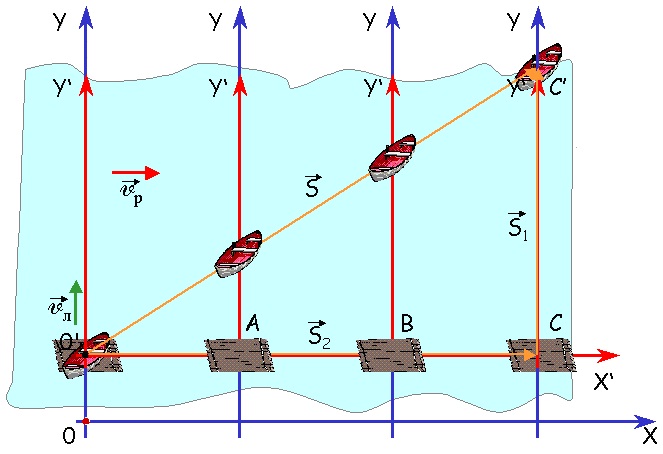
Лодка пересекает реку перпендикулярно течению реки двигаясь с некоторой скоростью относительно воды. За движением лодки следят 2 наблюдателя: один неподвижный на берегу, другой на плоту, плывущем по течению. Относительно воды плот неподвижен, а по отношению к берегу он движется со скоростью течения.

С каждым наблюдателем свяжем систему координат.

X0Y – неподвижная система координат.

X’0’Y’ – подвижная система координат.

S – перемещение лодки относительно неподвижной СО.

S₁ – перемещение лодки относительно подвижной СО

S₂ – перемещение подвижной системы отсчета относительно неподвижной СО.

По закону сложения векторов

Скорость получим разделив S на t:

v – скорость тела относительно неподвижной СО

v₁ – скорость тела относительно подвижной СО

v₂ – скорость подвижной системы отсчета относительно неподвижной СО

Эта формула выражает классический закон сложения скоростей: скорость тела относительно неподвижной СО равна геометрической сумме скорости тела относительно подвижной СО и скорости подвижной СО относительно неподвижной СО.

В скалярном виде формула будет иметь вид:

Впервые эту формулу получил Галилей.

Принцип относительности Галилея: все инерциальные системы отсчета равноправны; ход времени, масса, ускорение и сила в них записываются одинаково.

Скачать презентацию с Яндекса

Источник

Относительность движения

Любое движение тела происходит по отношению к другим телам. Физики говорят: «Относительно других тел».

К примеру, человек, едущий в автобусе, относительно автобуса находится в состоянии покоя, а относительно дороги – движется.

Примечание: Когда мы рассматриваем движение тела, мы выбираем систему отсчета, в которой это дело будет двигаться. При этом, тело отсчета мы принимаем за неподвижное тело, относительно которого происходит движение изучаемого тела.

в разных системах отсчета (СО) будут различаться.

Траектория тела различна в разных системах отсчета

Траектория – это относительная характеристика движения. Потому, что она различается для разных систем отсчета (СО).

В то время, пока самолет летит, точка, лежащая на кончике его винта, относительно самолета движется по окружности (рис. 1), а относительно неподвижного наблюдателя на земле – эта же точка имеет винтовую траекторию.

Например, движение ниппеля велосипедного колеса во время поездки на велосипеде.

В системе отсчета, связанной с:

Что такое циклоида

Циклоида – это плоская кривая линия. По такой линии движется точка, лежащая на окружности, когда эта окружность катится по прямой без проскальзывания (рис. 2).

Циклоиду называют трансцендентной кривой линией.

Линия трансцендентная, если ее в прямоугольных координатах не получается описать с помощью алгебраического уравнения.

Но с помощью параметра t можно записать отдельно координату x и координату y с помощью таких уравнений:

\[ \large \begin x = r \cdot t — r \cdot sin(t) \\ y = r — r \cdot cos(t) \end \]

Примечания:

Циклоиду впервые изучил Галилео Галилей. Этот выдающийся итальянский ученый занимался физикой, математикой, астрономией, механикой и философией.

А английский математик и архитектор Кристофер Рен в 1658 году посчитал длину арки циклоиды.

Длина циклоиды равна четырем диаметрам производящей окружности.

Кристофер Рен спроектировал и руководил возведением в Лондоне купола собора Святого Павла.

С помощью циклоиды братья Бернулли решили задачу о скорейшем спуске — брахистохроне. Брахистохрон – с греч. «Краткое время». Они доказали, что по желобу, имеющему форму перевернутой вниз циклоиды шарик скатывается вниз за кратчайшее из возможных время.

Скорость тела различна в разных системах отсчета

Рассмотрим движение человека в едущем по прямому участку пути трамвае (рис. 3).

Скорость трамвая \(\large \vec>>\) 60 километров в час. Предположим, в движущемся вагоне трамвая человек перемещается от задней части трамвая к его передней части, со скоростью \(\large \vec>>\) 3 километра в час.

Тогда скорость человека относительно трамвая будет равна 3 километрам в час, а относительно земли – 63 километрам в час.

Как переходить из одной системы отсчета в другую

Любое движение, которое мы рассматриваем, а, так же, его характеристики, будут различаться в разных системах отсчета.

Относительно одних тел рассматриваемое тело может покоиться, а вместе с тем, относительно других тел оно может находиться в движении.

Чтобы осуществить переход между системами отсчета, нужно применять закон сложения скоростей и перемещений. Скорость и перемещение – это векторы. Значит, будем складывать их геометрически. То есть, при сложении векторов будем учитывать их направления.

Примечание: Ньютон изучал движение тел. В его теории время протекает одинаково во всех системах отсчета. То есть, в механике Ньютона время – это абсолютная величина.

Представим себе такую картину: На берегу реки сидит и отдыхает девушка (рис. 4). По реке мимо нее проплывает плот (по течению). С плота в это время в воду прыгает молодой человек и вплавь добирается к противоположному берегу реки. После чего, садится на берег и отдыхает.

Перемещение в различных системах отсчета

Сначала запишем перемещение парня в системе отсчета, связанной с девушкой, когда нам известны его перемещение в системе отсчета, связанной с плотом.

Примечание:

На рисунке перемещение плота и перемещение парня относительно плота обозначены длинными черными стрелками. А перемещение парня относительно сидящей на берегу девушки обозначено длинной синей стрелкой.

Из рисунка видно, что векторы перемещений образуют прямоугольный треугольник.

Сложив вектор переносного и относительного перемещений, получим вектор абсолютного перемещения:

\( \large \overrightarrow>> \) – вектор перемещения плота;

\( \large \overrightarrow>> \) – вектор перемещения парня относительно плота (собственное перемещение парня);

\( \large \overrightarrow>> \) – вектор перемещения парня относительно девушки на берегу;

Длину вектора абсолютного перемещения можно найти по теореме Пифагора:

Скорость в различных системах отсчета

Запишем еще раз формулу для связи перемещений:

Зная перемещение, и время равномерного движения, можно найти модуль вектора скорости, т. е. длину вектора скорости.

Скорость плывущего плота и скорость парня не изменяются. Поэтому, для связи скорости и перемещения можно применить формулу

Разделив обе части этого уравнения на время t, получим выражение для скорости равномерного движения:

Обе части уравнения для перемещений разделим на время t движения.

Полученное выражение можно записать с помощью векторов скоростей:

В частности, на рисунке 4 красными векторами обозначены скорость реки (плота) и скорость парня.

Опишем обозначения, использованные нами в уравнении, связывающем скорости в различных системах отсчета:

\( \large \overrightarrow>> = \overrightarrow>> \) – вектор скорости парня;

\( \large \overrightarrow>> = \overrightarrow>> \) – вектор скорости плота (течения реки);

\( \large \overrightarrow>> \) – вектор скорости парня относительно девушки;

Длину вектора скорости найдем по теореме Пифагора:

Таким образом, до прыжка в воду скорость парня в системе отсчета, связанной с плотом, равнялась нулю (рис. 5).

А в системе отсчета, связанной с отдыхающей на берегу девушкой, скорость парня равнялась скорости течения реки (скорости плота).

После прыжка с плота в системе отсчета, связанной с плотом, скорость парня равняется скорости, с которой он плывет к берегу перпендикулярно течению реки.

Ну а в системе отсчета, связанной с девушкой, скорость парня – это векторная сумма скорости течения реки и скорости плавания парня.

Источник