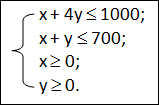в чем заключается математическая задача получения оптимального плана

Знания в формате 4 и 5

Меню навигации

Пользовательские ссылки

Информация о пользователе

Вы здесь » Знания в формате 4 и 5 » 11 класс (Семакин И.Г.) » П/р № 3.19. Решение задач оптимального планирования в Microsoft Excel

П/р № 3.19. Решение задач оптимального планирования в Microsoft Excel

Сообщений 1 страница 1 из 1

Поделиться12013-02-07 09:28:01

Цель работы: получение представления о построении оптимального плана методом линейного программирования; практическое освоение раздела Microsoft Excel «Поиск решения» для построения оптимального плана.
Используемое программное обеспечение: табличный процессор Microsoft Excel.

Справочная информация

Средство, которое используется в данной работе, называется Поиск решения. Соответствующая команда находится в меню Сервис. Поиск решения — одно из самых мощных средств табличного процессора Excel.

Задание 1

Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности условий можно приготовить не более 700 штук изделий. Рабочий день длится 8 часов. За день можно произвести не более 250 пирожных, пирожков – 1000 (по отдельности).
Стоимость пирожного вдвое выше стоимости пирожка. Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку.

Реализуем поиск оптимального решения для задачи планирования работы школьного кондитерского цеха;

1. Подготовить таблицу к решению задачи оптимального планирования.

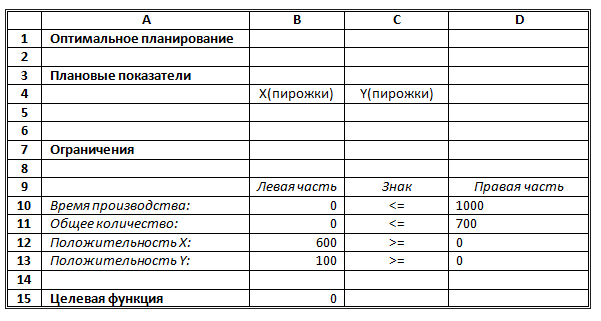
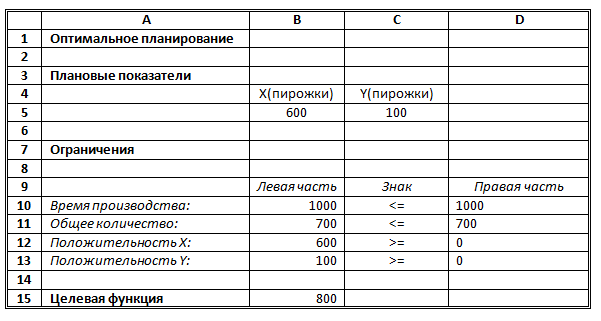
В режиме отображения формул таблица показана на рисунке. Ячейки В5 и С5 зарезервированы соответственно для значений х (план по изготовлению пирожков) и у (план по изготовлению пирожных). Ниже представлена система неравенств, определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция занесена в ячейку В15.

Формулы:
B10=B5+4*C5
B11=B5+C5
B15=B5+2*C5

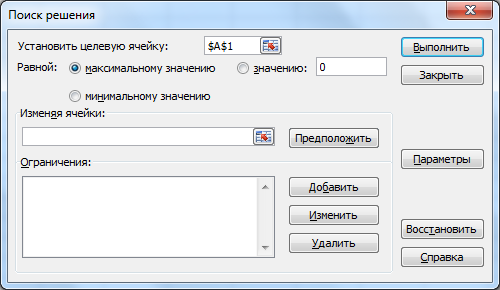
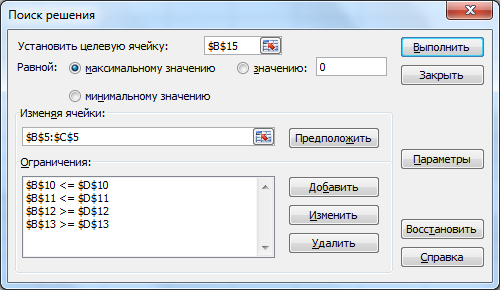
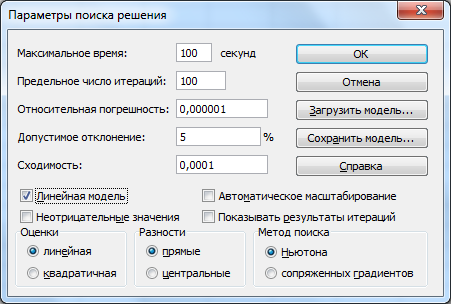
=> указать, что задача является линейной (это многократно облегчит программе ее решение). Для этого щелкнуть на кнопке Параметры, после чего открывается форма Параметры поиска решения:

=> установить флажок линейная модель. Остальная информация на форме Параметры поиска решения чисто служебная, автоматически устанавливаемые значения нас устраивают, и вникать в их смысл не будем. Щелкнуть на кнопке ОК. Снова откроется форма Поиск решения.
=> щелкнуть на кнопке Выполнить — в ячейках B5 и С5 появляется оптимальное решение:

Справочная информация

В результате применения инструмента Поиск решения, получен следующий оптимальный план дневного производства кондитерского цеха:
нужно выпускать 600 пирожков и 100 пирожных. Эти плановые показатели соответствуют положению точки В на рис. 6.9 в учебнике. В этой точке значение целевой функции /(600, 100) = 800. Если один пирожок стоит 5 руб., то полученная выручка составит 4000 руб.

Задание 2

Требуется решить задачу поиска оптимального плана производства школьного кондитерского цеха с измененными условиями.
Представьте себе, что в школе учатся неисправимые сладкоежки. И, кроме всех прочих ограничений, перед кондитерским цехом ставится обязательное условие: число пирожных должны быть не меньше числа пирожков. При такой постановке задачи система неравенств примет вид:

1. Внести соответствующие изменения в электронную таблицу, построенную при выполнении предыдущего задания.
2. Получить оптимальный план с помощью средства Поиск решения.
3. Проанализировать полученные результаты. Сопоставить их с результатами задания 1.

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

В чем состоит задача оптимального планирования?

а) В чем состоит задача оптимального планирования?

б) Что такое плановые показатели, ресурсы, стратегическая цель? Приведите примеры.

Ответ

Оптимальное планирование

Задача оптимального планирования заключается в определении значений плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели.

Проблема, к обсуждению которой мы теперь переходим, называется оптимальным планированием. Объектами планирования могут быть самые разные системы: деятельность отдельного предприятия, отрасли промышленности или сельского хозяйства, региона, наконец государства.

Постановка задачи планирования выглядит следующим образом:

• имеются некоторые плановые показатели: X, Y, и др.;
• имеются некоторые ресурсы: R1, R2 и др., за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены;
• имеется определенная стратегическая цель, зависящая от значений X, Y и др. плановых показателей, на которую следует ориентировать планирование.

Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.

Источник

В чем заключается математическая задача получения оптимального плана

12.4. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ПЛАНА

С помощью рассмотренных методов построения первоначального опорного плана можно получить вырожденный или невырожденный опорный план. Построенный план транспортной задачи как задачи линейного программирования можно было бы довести до оптимального с помощью симплексного метода. Однако из-за громоздкости симплексных таблиц, содержащих mn неизвестных, и большого объема вычислительных работ для получения оптимального плана используют более простые методы. Наиболее часто применяются метод потенциалов (модифицированный распределительный метод) и метод дифференциальных рент.

Метод потенциалов. Общий принцип определения оптимального плана транспортной задачи этим методом аналогичен принципу решения задачи линейного программирования симплексным методом, а именно: сначала находят опорный план транспортной задачи, а затем его последовательно улучшают до получения оптимального плана.

Теорема 12.2 (критерий оптимальности). Для того чтобы допустимый план перевозок в транспортной задаче был оптимальным, необходимо и достаточно, чтобы существовали такие числа и , что

(12.4)

(12.5)

Числа и называют потенциалами пунктов отправления и назначения соответственно.

Сформулированная теорема позволяет построить алгоритм нахождения решения транспортной задачи. Он состоит в следующем. Пусть одним из рассмотренных выше методов найден опорный план. Для этого плана, в котором m + n – 1 базисных клеток, можно определить потенциалы и так, чтобы выполнялось условие (12.4). Поскольку система (12.4) содержит m + n – 1 уравнений и m + n неизвестных, то одну из них можно задать произвольно (например, приравнять к нулю). После этого из m + n – 1 уравнений (12.4) определяются остальные потенциалы и для каждой из свободных клеток вычисляются величины . Если оказалось, что , то план оптимален. Если же хотя бы в одной свободной клетке , то план не является оптимальным и может быть улучшен путем переноса по циклу, соответствующему данной свободной клетке.

Циклом в таблице условий транспортной задачи, называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья – вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое – в столбце. Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами.

Процесс улучшения плана продолжается до тех пор, пока не будут выполнены условия (12.5).

Пример. На три базы поступил однородный груз, который требуется перевезти в четыре пункта назначения . Тарифы перевозок, запасы и потребности указаны в таблице 12.3. Спланировать перевозки так, чтобы их общая стоимость была минимальной.

Источник

Примеры решения задач на оптимальное планирование.

Выбранный для просмотра документ Вариант 2.doc

Фирма выпускает кастрюли и кофеварки, используя листовой металл на корпуса, полосовой металл на ручки и заклепки в качестве соединительных элементов. Количество единиц каждого ресурса, идущего на производство единицы товара, максимальный запас каждого ресурса, доход от единицы товара приведены в таблице.

Максимизировать доход производителя.

Максимум прибыли в 331 руб. достигается при выпуске 23 кофеварок и 14 кастрюль.

Конкуренция приводит к необходимости торговым предприятиям заниматься еще и выпуском продукции собственного производства, например салатов, пиццы и т.п. Нормы затрат на производство разных видов пиццы, объемы ресурсов и стоимость приведены в таблице.

Нормы затрат на изготовление 100 шт. пиццы, кг

Запасы продуктов, кг

Цена за 100 шт., тыс. руб.

Рисунок 3 – вид задачи до поиска решения

Рисунок 4 – вид задачи после поиска решения.

Максимальная прибыль в 22,5 тыс. получается при выпуске 2500 пицц «ассорти»

Найдите минимум целевой функции при указанных ограничениях

Рисунок 5 – графический способ решения задачи оптимизации. F ( x )= 2 x 1+5 x 2=2*4+0*0=8

Найдите минимум целевой функции при указанных ограничениях.

Рисунок 6 – Графическое решение задачи.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Методическая работа в онлайн-образовании

Курс профессиональной переподготовки

Математика и информатика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Рассмотрены 4 задачи по оптимальному планированию и методы их решения. Образцы решения представлены в приложенном архиве. Задачи решены с помощью MS Excel и графическим способом.

Задача 1. Фирма выпускает кастрюли и кофеварки, используя листовой металл на корпуса, полосовой металл на ручки и заклепки в качестве соединительных элементов.

Задача 2 Конкуренция приводит к необходимости торговым предприятиям заниматься еще и выпуском продукции собственного производства, например салатов, пиццы и т.п.

Номер материала: ДБ-1416144

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минобрнауки планирует учредить стипендию для студентов-философов

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В России отцы охотнее дают деньги детям на карманные расходы, чем матери

Время чтения: 2 минуты

Учителя Кубани смогут получить миллион рублей на взнос по ипотеке

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Бельгийский город будет платить детям виртуальные деньги за отказ от неэкологичного транспорта

Время чтения: 0 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Модели оптимального планирования

Урок 30. Информатика 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Модели оптимального планирования»

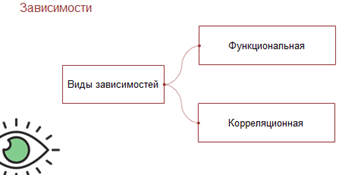
Сегодня на уроке мы с вами заканчиваем изучение теоретических основ «Информационного моделирования». На прошлом уроке мы занимались моделированием корреляционных зависимостей. И узнали, что существует два вида зависимостей. Уже хорошо знакомая функциональная зависимость (когда определённому значению независимой переменной соответствует строго определённое значение зависимой переменной) и корреляционная.

Корреляционная зависимость – это такая зависимость, когда данному значению одной величины соответствует целый ряд значений другой, причём при изменении данной величины меняются и другие значения, а также и его среднее. То есть зависимость между величинами, каждая из которых подвергается неконтролируемому разбросу.

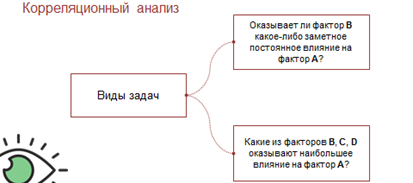
При изучении корреляционных зависимостей мы рассмотрели два вида задач.

Первый вид – Оказывает ли фактор В какое-либо заметное постоянное влияние на фактор А?

Второй – Какие из факторов B, C или D оказывают наибольшее влияние на фактор А?

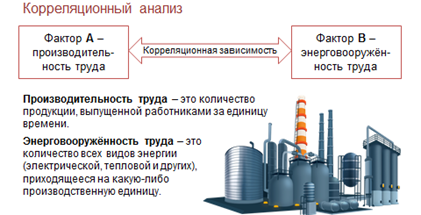
Так же мы узнали, что раздел математической статистики, который исследует корреляционные зависимости, называется корреляционным анализом.

Затем, рассмотрев пример корреляционной зависимости, мы пришли к тому, что оценку корреляции величин начинают с высказывания гипотезы о возможном характере зависимости между их значениями.

Чаще всего считают, что это линейная зависимость. Тогда мера корреляционной зависимости – это величина, которая называется коэффициентом корреляции.

Но существуют задачи другого типа.

На прошлом уроке мы рассмотрели зависимость производительности труда рабочего на предприятии от энерговооружённости данного предприятия, то есть от условий работы, которые предприятие создаёт для своего рабочего.

Но для того чтобы предприятие развивалось и модернизировалось нужно научиться оптимально использовать ресурсы при производственном планировании. Например, научиться находить оптимальные комбинации различных видов продукции для хранения на складах. А также минимизировать транспортные расходы, при перевозке продукции.

Сегодня на уроке мы свами будем разбираться со следующими вопросами:

· Что такое оптимальное планирование и в чём состоит задача оптимального планирования.

· Что такое плановые показатели, ресурсы и цели.

· А также, какое программирование называется математическим, а какое линейным.

Объектом планирования может стать любая система: от детского сада до предприятия-гиганта, любая отрасль промышленности или сельского хозяйства, любой регион и, наконец, государство.

При постановке задачи учитывают следующее:

· Имеющиеся плановые показатели: икс, игрек и другие:

· Имеющиеся ресурсы: R1, R2 и другие. За счёт ресурсов достигаются плановые показатели. Но ресурсы практически всегда ограничены.

· И стратегическая цель. Цель зависит от значений плановых показателей и на неё ориентируются при планировании.

Тогда оптимальным планом называется значение плановых показателей при достижении стратегической цели, с учётом ограниченности ресурсов.

Пусть объектом планирования является транспортная компания, которая занимается доставкой товаров из нескольких предприятий, нескольким потребителям.

Основными ресурсами транспортной компании будут транспортные средства, необходимые для перевозки товаров, а также расходы на перевозку. Стратегической целью данной компании будет планирование маршрута так, чтобы расходы на перевозку были минимальными.

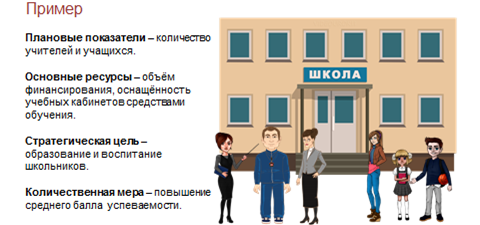
Или другой пример: Пусть объектом моделирования является средняя общеобразовательная школа.

Плановыми показателями здесь могут выступить, например, количество учителей и учащихся. Основными ресурсами деятельности школы являются объём финансирования, оснащённость учебных кабинетов средствами обучения, например, учебными стендами, плакатами, интерактивной доской и компьютерами. Естественно в школе стратегической целью является образование и воспитание школьников. А количественной мерой будет повышение среднего балла успеваемости.

На уроках информатики логично, для решения задач использовать компьютер. Следовательно, нужно информационную модель преобразовать в математическую, то есть представить в виде формул, уравнений и других средств математики.

Давайте рассмотрим пример решения задачи оптимального планирования с помощью компьютера.

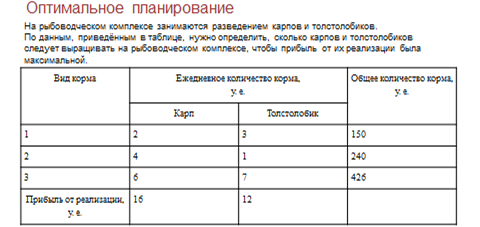
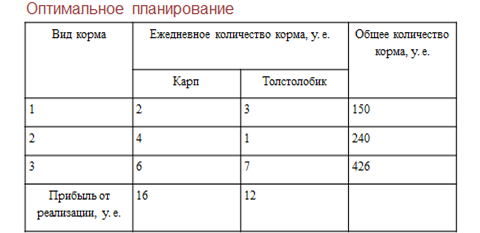
На рыбоводческом комплексе занимаются разведением карпов и толстолобиков. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество корма каждого вида, которое должны ежедневно получать карпы и толстолобики, приведено в таблице. В ней же указаны общее количество корма каждого вида, которое может быть использовано комплексом, а также прибыль от реализации рыбы.

Нужно определить, сколько карпов и толстолобиков следует выращивать на рыбоводческом комплексе, чтобы прибыль от их реализации максимальной.

Естественно, что это чисто учебный пример. Вряд ли существует такой рыбоводческий комплекс, который занимается разведением всего двух видов рыб, да и наибольшая выручка – это не единственная цель его работы.

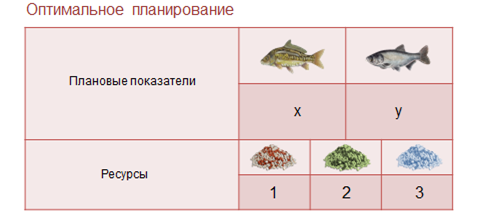
Итак, здесь плановыми показателями являются:

Икс штук – карпов и игрек штук – толстолобиков.

Ресурсами в этом примере можно назвать количество корма каждого вида, которое должны ежедневно получать карпы и толстолобики.

Для упрощения решения задачи, будем считать, что другие ресурсы, например, электроэнергия, не ограничены.

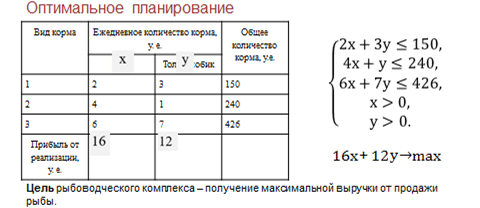
Из условия задачи известно, что для обеспечения нормальных условий выращивания карпов и толстолобиков используются три вида кормов. Также известно количество корма каждого вида, которое должны ежедневно получать карпы и толстолобики, и общее количество корма каждого вида, которое может быть использовано рыбоводческим комплексом. Составим систему неравенств.

Итак, для первого корма. Ежедневно карпы должны получать 2 единицы первого корма, а толстолобики 3 единицы, но в месяц количество потребления первого корма рыбами не должно превышать 150-ти единиц.

Аналогично составим неравенства для второго и третьего корма.

К трём полученным неравенствам нужно добавить условия положительности значений величин икс и игрек, так как не может быть отрицательное число карпов и толстолобиков. В итоге получим следующую систему неравенств.

Теперь сформулируем стратегическую цель. Нам нужно определить, сколько карпов и толстолобиков следует выращивать на рыбоводческом комплексе, чтобы прибыль от реализации рыбы была максимальной.

По условию мы знаем, что прибыль от реализации одного карпа равна 16 условным единицам, а толстолобика – 12 у.е., тогда сумма 16x+12y должна стремиться к максимуму.

Цель рыбоводческого комплекса – получение максимальной выручки от продажи рыбы.

Рассмотрим записанное выражение как функцию от x, y.

То есть f_xy, игрек равно 16x + 12y.

Такая функция называется целевой функцией.

Следовательно, получение оптимального плана свелось к следующей математической задаче:

Требуется найти значения плановых показателей x и y, которые будут удовлетворять данной системе неравенств и придавать максимальное значение целевой функции.

Итак, мы построили математическую модель задачи оптимального планирования для рыбоводческого комплекса.

Решить данную задачу нам помогут средства, реализованные в табличном процессоре Excel.

Математическое программирование — это раздел математики, содержащий методы решения задач оптимального планирования.

Так как в целевую функцию f_xy игрек величины икс и игрек входят линейно, то есть они в первой степени, то нашу задачу можно отнести к разделу этой науки, который называется линейное программирование.

Линейное программирование – это раздел математического программирования, решающий задачи оптимального планирования с линейной целевой функцией.

Для решения задачи в MS Excel, создадим таблицу с исходными данными.

Ячейки В7 и С7 оставим соответственно для значений х (количество выращиваемых карпов) и у (количество выращиваемых толстолобиков).

В ячейки В2:С2 введём коэффициенты в ограничениях по первому корму, то есть 2 и 3 соответственно. В ячейки В3:С3 по второму корму. И в В4:С4 по третьему. Далее В диапазон ячеек Д2:Д4 запишем общее количество корма каждого вида, которое может быть использовано комплексом.

В ячейки В6 и С6 запишем коэффициенты целевой функции, в нашем случае это 16 и 12.

Далее в ячейку В8 введём формулу целевой функции. Будем использовать встроенную функцию СУММПРОИЗВ.

Данная функция перемножает соответствующие элементы заданных списков, а затем складывает полученные произведения.

Аргументами функции СУММПРОИЗВ являются диапазоны ячеек, причём все диапазоны должны иметь одинаковые размерности.

Встроенная функция СУММПРОИЗВ будет записываться следующим образом: равно СУММПРОИЗВ, далее в круглых скобках нужно указать два диапазона ячеек, которые нужно перемножить и затем сложить произведения. В нашей задаче целевая функция записана следующим образом: шестнадцать икс плюс двенадцать игрек, то есть нам нужно найти сумму произведений коэффициентов целевой функции и переменных. Указываем первый диапазон В6:С6 точка с запятой и второй диапазон В7:С7.

Функция СУММПРОИЗВ перемножит соответствующие ячейки диапазона, то есть В6 умножит на В7, а С6 умножит на С7. Затем полученные произведения суммирует.

В ячейку Е2 введём ограничения. Снова будем использовать встроенную функцию СУММПРОИЗВ. Здесь первый диапазон ячеек – это коэффициенты в ограничениях для первого корма, а второй – переменные. Аналогично заполним ограничения для второго и третьего корма.

Теперь необходимо вызвать программу оптимизации и сообщить ей, где расположены данные. Для этого необходимо сначала загрузить её.

Откроим вкладку Файл и выберем пункт Параметры. Далее выбираем команду Надстройки, а затем в окне Управление выбираем пункт Надстройки Excel. Нажимаем кнопку Перейти. Теперь в окне Доступные надстройки установим флажок Поиск решения и нажимаем кнопку ОК.

После загрузки надстройки «Поиск решения» на вкладки Данные в группе Анализ становится доступна команда Поиск решения. Выбираем её, после чего перед нами открывается соответствующая форма.

Далее необходимо выполнить следующий алгоритм:

Ввести координату ячейки с целевой функцией. В нашем случае это В8. (Заметим, что если перед этим установить курсор на ячейку В8, то ввод произойдёт автоматически).

Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.

В поле «Изменяя ячейки переменных» ввести В7:С7, то есть сообщить, какое место отведено под значения переменных-плановых показателей.

В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях следующим образом: щёлкнуть по кнопке «Добавить».

Итак, первое неравенство имеет вид 150 больше либо равно два икс плюс три игрек. Теперь в появившемся диалоговом окне «Добавление ограничения» ввести ссылку на ячейку Д2, выбрать из меню знак неравенства больше либо равно и ввести ссылку на ячейку Е2; снова щёлкнуть по кнопке «добавить» и аналогично ввести второе ограничение Д3 больше либо равно Е3 и так далее. В конце нажимаем ОК.

Закрываем диалоговое окно «Добавление ограничения». Снова появится форма «Поиск решения». После завершения ввода всех ограничений и параметров нажимаем «Найти решение» и получаем искомое решение задачи.

То есть в результате применения инструмента Поиск решения получен следующий оптимальный план разведения карпов и толстолобиков на рыбоводческом комплексе: нужно вырастить 57 карпов и 12 толстолобиков.

Решение данной задачи может быть представлено и в дробных числах, но так как у нас в задаче надо найти количество рыб, а оно не может быть дробным числом, мы числа округляем до целых.

Представим систему полученных нами неравенств на координатной плоскости.

То есть нам нужно изобразить пять прямых, соответствующих следующим линейным уравнениям:

В результате мы получим четырёхугольник ABCD. Любая точка четырёхугольника является решением нашей системы неравенств. Если икс равно 57, а игрек равно 12, то в этой точке значение целевой функции Эф от пятидесяти семи и двенадцати равно 1056. Если один карп стоит 16 условных единиц, а толстолобик 12, то полученная выручка составит 1056 условных единиц. Этой точке соответствует точка Бэ на нашем графике.

Итак, сегодня на уроке мы с вами построили модель оптимального планирования на рыбоводческом комплексе.

А теперь давайте повторим всё, что мы узнали сегодня на уроке:

Оптимальное планирование — это определение значений плановых показателей с учётом ограниченности ресурсов при условии достижения заданной цели.

Ограниченность ресурсов может описываться с помощью:

Цель описывается функцией, для которой требуется найти минимум или максимум.

Microsoft Excel имеет специальное средство Поиск решения для решения задач оптимального планирования.

Источник