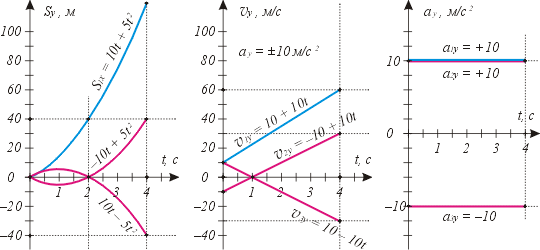в чем заключается графический способ описания движения
Способы описания движения – система отчета механического
Кинематика – это раздел механики, изучающий движения тел вне зависимости от их причин. Для описания движения применяется ряд способов, обзор которых предлагается в данной статье.
Движение и его описание
Суть любого механического движения состоит в том, что тела меняют свое положение с течением времени. Главная задача кинематики состоит в том, чтобы находить это положение в любой указанный момент времени, как прошлого, так и будущего.
Для решения этой задачи движение необходимо описать так, чтобы описание выявляло закономерности, по которым происходит изменение положения тел. А дальше, задаваясь нужным моментом времени и сформулированным описанием – можно найти положение тела без непосредственного ожидания и измерения.
Таким образом, описание движения позволяет понять события, произошедшие в прошлом и будущем (иногда в далеком).
Способы описания движения
Любое описание движения заключается в том, чтобы найти связь между координатами тела в выбранной Системе Отсчета с моментами времени в этой же Системе. Если эта связь задана, то выбрав необходимый момент, можно получить координаты тела в это время.
Рис. 1. Способы описания движения – табличный, графический, аналитический.
Табличный способ
Исторически первым способом описания движения стал табличный. Он заключается в том, чтобы отмечать координаты тела в некоторые моменты времени. По представленному ряду пар «время – координата» мы можем видеть, в какие моменты прошлого тело двигалось быстрее, в какие медленнее, и когда где оно было.
Безусловно, такой способ самый грубый, поскольку моменты времени в таблице не обязательно будут равномерными, и, кроме того, таблица не дает представления о том, в каких точках находилось тело в моменты времени, не указанные в таблице. Однако, зачастую это и не требуется. Поэтому табличный способ описания движения до сих пор находит применение. В современных условиях для этого чаще всего используют стробоскопическую фотографию. Освещая тело в ряд моментов, можно зафиксировать положение тела в эти моменты.
Рис. 2. Стробоскопическое фото движения.
Например, бросив тело с начальной высоты 2м вверх со скоростью 5м/с, и настроив стобоскоп на промежуток 0.2с, можно получить следующую таблицу, описывающую движение:
Время, с
Координата, м
Любое описания путешествий является таким табличным способом, поскольку везде, как правило, указывается ряд пар «место, где был путешественник – время, когда он туда прибыл».
Графический способ
Самым наглядным описанием движения является графический способ. Откладывая на оси абсцисс время, а на оси ординат расстояние – можно получить график, по которому положение тела в пространстве определяется в любой нужный момент. Кроме того, такой график дает наглядное представление о скорости изменения координаты.
Рис. 3. Пример графика зависимости расстояния от времени.
График зависимости координаты от времени ничего не говорит о траектории пути! График может быть прямой, а траектория – извилистой, и наоборот. Например, для случая, рассмотренного выше (тело, брошенное вверх), график координаты будет параболой. А траектория пути – прямой.
Аналитический способ
Наиболее полным и точным способом описания движения является аналитический, то есть, заданный математически.
Поскольку любая функция выражает зависимость, а описание движение и есть описание зависимости расстояния от времени – то во многих случаях данную зависимость можно выразить функцией. Задавшись такой функцией, и подставляя в качестве исходной переменной нужный момент времени – мы можем получить координату в этот момент.
Для примера, рассмотренного выше (тело, брошенное вверх), математическая функция, описывающая движение тела, выглядит следующим образом:
К сожалению, для большинства движений точное аналитическое описание слишком сложно (например, учет сопротивления воздуха сильно усложняет приведенную формулу). Однако, аналитический способ позволяет выделить наиболее важную компоненту движения, и описать ее наиболее удобным для дальнейшего использования образом.
Что мы узнали?
Описание движения устанавливает закономерности, с которыми тело меняло свое положение в пространстве. Они позволяют узнать положение тела в любой момент в прошлом, и спрогнозировать положение в будущем. Для описания движения применяется три способа: табличный, графический и аналитический.
Графическое описание движений
В самом начале изучения кинематики мы отметили, что движение тел можно описывать графически, и привели пример графика зависимости пути от времени (см. § 12-а). Теперь мы знаем, что движение тел характеризуется и другими величинами: перемещением, скоростью, ускорением. Они тоже могут быть отражены на графиках.
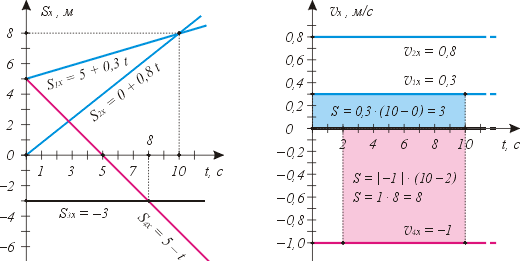
Графики для прямолинейного равномерного движения:
Слева – графики зависимости от времени проекций перемещений четырёх разных тел, движущихся с различными скоростями. Медленнее всех вдоль оси Х движется первое тело: его скорость 0,3 м/с сонаправлена оси X. Быстрее всех движется четвёртое тело: его скорость 1 м/с противонаправлена оси Х (на что указывает отрицательное значение проекции). Точка пересечения графиков в момент времени 10 с означает, что тела 1 и 2 имели равные проекции перемещений: 8 м. Аналогично, тела 3 и 4 в момент времени 8 с тоже имели равные проекции перемещений: по –3 м. А что вы скажете про 2 и 4 тела?
Справа – графики зависимости от времени проекций скоростей этих тел (на прежнюю ось). Все четыре линии показывают, что все проекции скоростей с течением времени не меняются. А что иллюстрируют цветные прямоугольники? – вероятно, спросите вы.
Обратим внимание: площадь прямоугольника, заключённого между линией графика проекции скорости, осью абсцисс и двумя выбранными ординатами, численно равна пути, пройденному телом за интервал времени между выбранными моментами. Например, площадь под первым графиком за интервал времени с 0 до 10 с численно равна трём. Взглянув на первый график слева, мы видим: проекция перемещения изменилась с 5 до 8 м, то есть на 3 м за то же время.
Графики для прямолинейного равноускоренного движения не для всех величин являются прямолинейными (см. выше). С чем это связано?
Как вы узнали в § 12-й, при равноускоренном движении проекции перемещения зависят от времени по квадратичному закону. Графически это выражается частями парабол (см. левую часть чертежа, внизу). Наряду с этим в § 12-и вы узнали, что при равноускоренном движении проекции мгновенной скорости зависят от времени по линейному закону. Графически это выражается прямыми линиями (см. среднюю часть чертежа, которую мы построили по значениям из левой части). Справа показано, что проекции ускорений тех же тел не изменяются с течением времени, так как их движения равноускоренные.
С точки зрения физики, графики зависимостей кинематических величин от времени несут ту же информацию, что и алгебраические формулы. Поэтому вы можете использовать алгебраический и графический способы как равноправные.
Графическое представление движения

Всего получено оценок: 69.
Всего получено оценок: 69.
Большую часть информации о мире человек получает с помощью зрения. Поэтому одними из наиболее используемых способов описания физических явлений являются графики. Рассмотрим особенности графического представления движения.
График координаты
Движение тела состоит в изменении его координат с течением времени. У тела всегда есть некоторые координаты, на прямой – одна, на плоскости – две, в пространстве – три. А значит, для любой координаты можно построить график ее зависимости от времени. По оси абсцисс на графике откладываются единицы времени, по оси ординат – единицы расстояния. Точки на графике будут представлять координату тела в соответствующие моменты.
Равномерное движение
В простейшем случае тело равномерно движется вдоль прямой, для описания такого движения достаточно одной координаты. Формула перемещения при равномерном движении:
Используя эту формулу, строим график.
Допустим, в начальный момент времени тело имеет координату 5, скорость движения 2. Получаем точки:
Построенный график – это прямая. По нему можно найти координату тела в любой момент времени.
Графическое представление равномерного движения всегда представляет собой прямую, пересекающую ось ординат в точке, равную начальной координате. Наклон прямой характеризует скорость равномерного движения – чем она больше, тем круче поднимается график. Если скорость отрицательна – то график будет нисходящим.
Неравномерное движение
Если тело движется неравномерно, и скорость его меняется, то график координаты будет более сложным.
Если тело сперва двигалось с одной скоростью, потом с другой, и так далее – он будет состоять из ряда прямолинейных участков, каждый из которых можно рассматривать, как отдельный график равномерного движения, при котором начальная координата участка равна конечной координате предыдущего участка. Например, пусть тело сперва двигается вперед (восходящая прямая), потом некоторое время стоит (горизонтальная прямая), а потом вернется (нисходящая прямая).
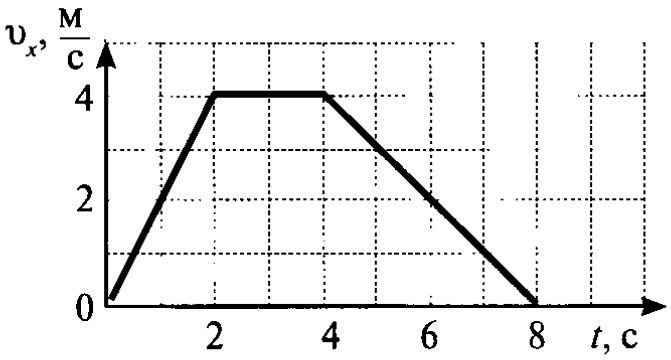
Наиболее сложный случай – когда тело постоянно плавно изменяет свою скорость. В этом случае график будет представлять собой плавную кривую. Например, если скорость равномерно увеличивается, то движение получается равноускоренным, и его графиком является восходящая парабола.
График скорости
Иногда удобно построить график скорости движения. Строится он точно так же, как и график координаты, но при этом по оси ординат откладываются значения скорости.
При равномерном движении скорость постоянна, а график постоянной величины представляет собой горизонтальную прямую. При нулевой скорости эта прямая совпадает с осью абсцисс.
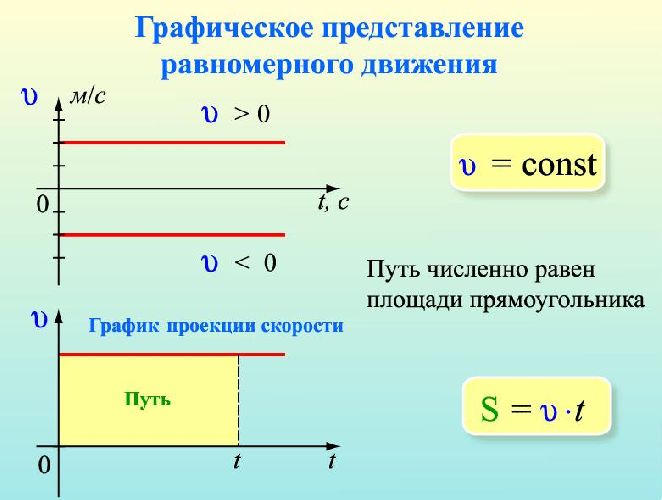
Если движение равноускоренное – то прямая будет восходящей или нисходящей.
График координаты и траектория
Иногда путают траекторию и график координаты. Это – не одно и то же.
Траектория – это линия, вдоль которой происходит движение. График же показывает зависимость координаты от времени. Например, если тело движется прямолинейно с остановками – его траектория будет прямой линией, а график координаты – ломанной, состоящей из наклонных и горизонтальных участков. Если тело движется равномерно по окружности, его траектория будет представлять собой круг, а графики обоих координат – синусоиды.
Что мы узнали?
Удобным способом описания движения является построение графиков координат. Для графического представления прямолинейного движения достаточно одного графика, для описания движения на плоскости – требуются два графика, в пространстве – три. Скорость также можно представить в виде графика.
Способы описания движения

Всего получено оценок: 223.
Всего получено оценок: 223.
Кинематика – это раздел механики, изучающий движения тел вне зависимости от их причин. Для описания движения применяется ряд способов, обзор которых предлагается в данной статье.
Движение и его описание
Суть любого механического движения состоит в том, что тела меняют свое положение с течением времени. Главная задача кинематики состоит в том, чтобы находить это положение в любой указанный момент времени, как прошлого, так и будущего.
Для решения этой задачи движение необходимо описать так, чтобы описание выявляло закономерности, по которым происходит изменение положения тел. А дальше, задаваясь нужным моментом времени и сформулированным описанием – можно найти положение тела без непосредственного ожидания и измерения.
Таким образом, описание движения позволяет понять события, произошедшие в прошлом и будущем (иногда в далеком).
Способы описания движения
Любое описание движения заключается в том, чтобы найти связь между координатами тела в выбранной Системе Отсчета с моментами времени в этой же Системе. Если эта связь задана, то выбрав необходимый момент, можно получить координаты тела в это время.
Табличный способ
Исторически первым способом описания движения стал табличный. Он заключается в том, чтобы отмечать координаты тела в некоторые моменты времени. По представленному ряду пар «время – координата» мы можем видеть, в какие моменты прошлого тело двигалось быстрее, в какие медленнее, и когда где оно было.
Безусловно, такой способ самый грубый, поскольку моменты времени в таблице не обязательно будут равномерными, и, кроме того, таблица не дает представления о том, в каких точках находилось тело в моменты времени, не указанные в таблице. Однако, зачастую это и не требуется. Поэтому табличный способ описания движения до сих пор находит применение. В современных условиях для этого чаще всего используют стробоскопическую фотографию. Освещая тело в ряд моментов, можно зафиксировать положение тела в эти моменты.
Например, бросив тело с начальной высоты 2м вверх со скоростью 5м/с, и настроив стобоскоп на промежуток 0.2с, можно получить следующую таблицу, описывающую движение:
Время, с
Координата, м
Любое описания путешествий является таким табличным способом, поскольку везде, как правило, указывается ряд пар «место, где был путешественник – время, когда он туда прибыл».
Графический способ
Самым наглядным описанием движения является графический способ. Откладывая на оси абсцисс время, а на оси ординат расстояние – можно получить график, по которому положение тела в пространстве определяется в любой нужный момент. Кроме того, такой график дает наглядное представление о скорости изменения координаты.
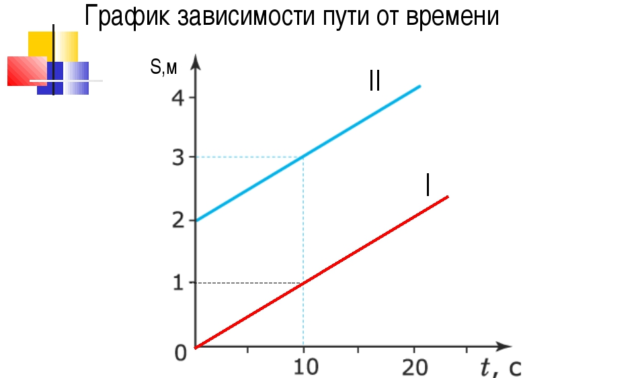
График зависимости координаты от времени ничего не говорит о траектории пути! График может быть прямой, а траектория – извилистой, и наоборот. Например, для случая, рассмотренного выше (тело, брошенное вверх), график координаты будет параболой. А траектория пути – прямой.
Аналитический способ
Наиболее полным и точным способом описания движения является аналитический, то есть, заданный математически.
Поскольку любая функция выражает зависимость, а описание движение и есть описание зависимости расстояния от времени – то во многих случаях данную зависимость можно выразить функцией. Задавшись такой функцией, и подставляя в качестве исходной переменной нужный момент времени – мы можем получить координату в этот момент.
Для примера, рассмотренного выше (тело, брошенное вверх), математическая функция, описывающая движение тела, выглядит следующим образом:
К сожалению, для большинства движений точное аналитическое описание слишком сложно (например, учет сопротивления воздуха сильно усложняет приведенную формулу). Однако, аналитический способ позволяет выделить наиболее важную компоненту движения, и описать ее наиболее удобным для дальнейшего использования образом.
Что мы узнали?
Описание движения устанавливает закономерности, с которыми тело меняло свое положение в пространстве. Они позволяют узнать положение тела в любой момент в прошлом, и спрогнозировать положение в будущем. Для описания движения применяется три способа: табличный, графический и аналитический.
ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ
Рисунок – источник и душа каждого
изображения и корень каждой науки.
Микеланджело
Для описания движения тела часто используется графический язык, когда на некоторой координатной плоскости строятся графики зависимости одного кинематического параметра от другого. Наиболее часто используются графики зависимости координаты, скорости или ускорения тела от времени, хотя возможны и другие варианты, например, зависимость одной координаты тела от другой, или скорости от координаты и т.д. Такой способ описания является достаточно удобным и плодотворным, поскольку позволяет как «увидеть» все движение в целом, так и выделить его наиболее характерные особенности.
Рассмотрим несколько примеров, в которых содержатся основные принципы построения графиков движений или извлечения из этих графиков той или иной информации о движении тела.
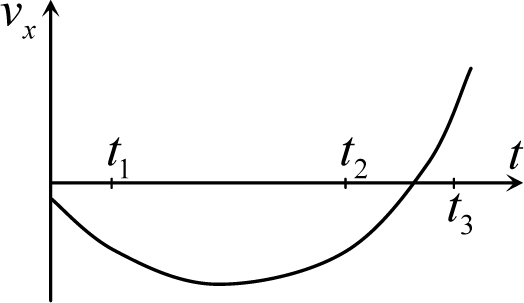
Пример 6.1. Тело движется прямолинейно вдоль некоторой оси x . На рис. 6.1 приведен график зависимости проекции скорости тела на ось x от времени. Сравнить проекции ускорения тела на ось x в моменты времени t 1 , t 2 и t 3 . Доказать, что на графике vx ( t ) не может быть разрывов.
Решение. Основная идея ответа на поставленный вопрос заключается в том, что мгновенному ускорению тела соответсвуют геометрические характеристики рассматриваемого графика. Для установления этого соответствия будем исходить из определения мгновенного ускорения в некоторый момент времени t :