в чем заключается гипотеза ампера
Гипотеза Ампера
Наблюдая сходство во взаимодействии катушек, по которым текут токи, и магнитов, Ампер предположил, что все магнитные взаимодействия обусловлены взаимодействием электрических токов. Это предположение получило название гипотезы Ампера.
Согласно этой гипотезе, свойства постоянных магнитов обусловлены циркулирующими в них одинаково направленными незатухающими «молекулярными» токами. Во внутренних частях магнита «соседние» молекулярные токи направлены противоположно и поэтому компенсируют друг друга. Но вблизи поверхности магнита эти токи текут в одном направлении, образуя как бы ток, обтекающий поверхность магнита (см. рис. 12.7).
Этот «поверхностный ток», как считал Ампер, и сообщает постоянному магниту его магнитные свойства.
Гипотеза Ампера объясняет также, почему не удается разъединить полюса магнита: ведь каждая половинка магнита снова подобна катушке с током.
В дальнейшем гипотеза Ампера подтвердилась лишь частично. Выяснилось, что «молекулярные» токи действительно существуют: они обусловлены движением электронов в атомах. Однако магнитное взаимодействие, связанное с этими токами, не может объяснить существования постоянных магнитов: во-первых, магнитное взаимодействие таких токов слишком слабо, во-вторых, эти токи ориентированы хаотично. «Секрет» постоянных магнитов оказался в другом.
Выяснилось, что каждый электрон (о существовании которых Ампер, конечно, не мог знать) сам по себе является микроскопическим магнитом. И в некоторых веществах, например в железе, электроны близко расположенных атомов ориентируются одинаково. Такие области одинаковой намагниченности называют «доменами». Каждый домен представляет собой крошечный магнитик, поэтому любой железный образец является как бы совокупностью очень маленьких магнитиков.
Обычно железный образец не проявляет магнитных свойств, так как домены в нем ориентированы хаотично. Но если поместить этот образец вблизи сильного магнита, то под действием магнита домены в образце через некоторое время ориентируются сходным образом.
И тогда этот железный образец сам станет постоянным магнитом.
Объясняем закон Ампера простым языком
Проводник, по которому течёт электрический ток, взаимодействует с существующими магнитными полями. На этом основана работа многих электротехнических устройств. Закон Ампера позволяет рассчитать такие взаимодействия. Он стал основой многих открытий в физике и часто применяется в современной технике. А имя Андре-Мари Ампера увековечено наряду с именами других 72 величайших ученых в списке, помещенном на первом этаже Эйфелевой башни.
Общее представление об электромагнитном поле
Длительное время представления об электрическом и магнитном поле не связывались между собой. Практические эксперименты подтверждали, что каждое из них имеет свои особенные свойства. Исследования Фарадея и Максвелла показали, что существует электромагнитное поле, которое может проявлять себя как электрическое или магнитное. Его можно описать с мощью вектора напряжённости. Если знать величину и направление данного вектора, то можно рассчитать силу воздействия.
Первым из учёных, кто обратил внимание на взаимное влияние магнитного поля и тока был известный учёный Х. К. Эрстед. Он исследовал влияние проводника с текущим по нему током на положение стрелки компаса. После этого учёные стали систематически изучать различные варианты взаимодействия.
Ампер появился на свет в 1775 году в Лионе. С детства он проявлял страсть к математике. Будучи подростком, изучал труды Эйлера и Лагранжа. Профессором математики Ампер стал в 1809 году, а в 1814 году был избран в академию наук. Хотя он преимущественно занимался математикой, его интересовала физика и некоторые другие науки.
Ампер был не первым человеком, который проявил интерес к связи магнитных и электрических полей, однако он впервые постарался найти точное математическое описание происходящих процессов. Им был не только установлен факт взаимодействия между электрическими токами, но и сформулирован закон данного явления.
Ампер доказал, что проводники начинают взаимодействовать, если по каждому из них протекает ток. В этом случае между ними возникают силы отталкивания или притягивания. В 1826 году Ампер впервые опубликовал результаты своего исследования, с помощью которого он изучал взаимодействие параллельных токов.
На рисунке ниже представлена схема одного из экспериментов Ампера, с помощью которого измеряется сила, действующая на проводник с током в магнитном поле. Стрелка красного цвета на рисунке показывает направление тока.
Основываясь на экспериментах, учёный сделал предположение, которое впоследствии получило название «гипотеза Ампера». Понимая, как влияет ток на магнитное поле, он сумел доказать, что вещество состоит из совокупности чрезвычайно маленьких круговых токов. Каждый из них порождает очень слабое магнитное поле. Поскольку все эти токи ориентированы хаотично, то внешне магнитное поле практически не проявляется. Однако в магнитах все круговые токи одинаково направлены и их воздействие складывается. Этим объясняются их особые свойства и практическое использование.
Ампер, используя свой закон, также объяснил эффект намагничивания. Согласно ему, у некоторых веществ под воздействием магнитного поля происходит упорядочивание круговых токов, и они постепенно ориентируются в одну сторону.
Эта гипотеза стала одним из источников теории магнетизма. Она смогла объяснить явление только частично, так как не дала ответа на вопрос о том, почему некоторые вещества подвергаются воздействию внешнего магнитного поля незначительно. Также остался необъяснённым вопрос, почему при намагничивании одни вещества создают магнитный поток сонаправленный внешнему полю (парамагнетики), а другие — противоположно направленный (диамагнетики).
Формулировка закона Ампера
При исследовании параллельных проводников с током было выяснено, что между ними действует сила притяжения, если токи однонаправленные, и отталкивания, если токи противоположно направленные. Сила взаимодействия токов зависит пропорционально от произведения сил токов и длины проводника. Справедливо также утверждение, что она обратно пропорциональна имеющемуся между проводами расстоянию. Математическая формулировка выглядит следующим образом:
Закон Ампера в такой формулировке показывает, что расчет силы магнитного поля производится по отношению к единице длины проводника. Силу, которую проводник с током испытывает в магнитном поле, называют силой Ампера.
Взаимодействие токов возможно лишь при наличии магнитных полей вокруг проводников. Эти поля создают движущиеся заряды. У магнитов постоянных магнитное поле, как утверждает закон Ампера, тоже возникает под воздействием электрических микротоков, но только тех, которые циркулируют внутри молекул вещества.
При описании магнитного поля принято использовать силовую характеристику, аналогичную вектору напряженности электрополя. Ее называют вектором магнитной индукции и обозначают латинской буквой «B». В системе СИ за единицу измерения данной характеристики принята Тесла: 1 Тл = 1 Н/А×м.
Направление вектора МИ определяется по правилу буравчика. Если штопор направить перпендикулярно плоскости проводника с током, то движение краёв рукоятки укажет направление вектора напряжённости. Подразумевается, что рукоятка будет вращаться по ходу часовой стрелки, если наблюдать сзади.
Взаимодействие тока и магнитного поля
Вектор магнитной индукции считается положительно направленным, если он совпадает с магнитной стрелкой, ориентированной на северный полюс. Используя это правило, можно определить направление вектора МИ в любой точке пространства и наглядно представить структуру магнитного поля. На рисунке ниже приведен пример расположения линий МИ для постоянного магнита и катушки с током.
Ампер смог рассчитать, как будет проходить взаимодействие между магнитным полем с заданной напряжённостью и проводником, по которому течёт ток. Согласно его закону действие магнитного поля на проводник с током описывается с помощью такой формулы:
Данная формула представлена в векторной форме. Умножение между векторами производится по особым правилам. В результате этой операции получится вектор, абсолютная величина которого определяется по следующей дифференциальной формуле:
Для прямолинейного провода данная формула в скалярной форме имеет вид:
Хотя, кажется, что закон достаточно прост, он стал важным достижением в развитии физической науки.
Направление электромагнитной силы
Если взять проводник с током и расположить его между полюсами магнита, как показано на рисунке ниже, то сила Ампера находится по формуле:
F = B × L × I, поскольку α = 90 градусов и sinα = 1.
Определение вектора действия силы выполняется согласно правилу левой руки. В этом случае нужно расположить ладонь левой руки перпендикулярно к силовым линиям магнитного поля. Пальцы при этом должны быть направлены в ту сторону, в которую течет ток. В таком положении перпендикулярно отставленный большой палец будет показывать направление электромагнитной силы.
При определении вектора силы, действующей на проводник, нужно учитывать, что ток всегда направлен от плюса к минусу. Это сложилось исторически, а потом стало традицией, несмотря на то, что в проводниках ток представляет собой движение электронов, то есть, отрицательных частиц.
В рассматриваемой ситуации можно регулировать силу взаимодействия, увеличивая или уменьшая силу тока. При этом напряжённость магнитного поля остается неизменной.
Проиллюстрировать применение правила левой руки можно на простом примере. Как уже было сказано выше, параллельные проводники с однонаправленными токами притягиваются. Правило поможет разобраться, почему это происходит.
Вокруг каждого проводника, по которому протекает ток, возникает магнитное поле. Нужно определить, как будет направлен вектор его напряжённости. Если взгляд направить вдоль проводника, то линии магнитной индукции поля будут видны в виде окружностей. Другими словами, если мысленно обхватить проводник правой рукой, направив большой палец по течению тока, то остальные четыре пальца будут соответствовать линиям напряженности магнитного поля.
Помещая первый проводник параллельно второму проводнику в магнитное поле, созданное последним, можно определить направление электромагнитной силы, используя правило левой руки. Расположив ее таким образом, чтобы получить линии МИ, входящие в ладонь, а направление пальцев, совпадающее с направлением тока, можно увидеть, что отогнутый большой палец указывает на второй проводник.
Понятно, что данное правило одинаково относится к обоим проводникам. Следовательно, можно определить направление электромагнитной силы в различных ситуациях. Аналогично можно видеть, что при противоположном направлении токов, действует сила отталкивания.
Влияние замкнутого контура
Используя закон Ампера можно сделать вывод о том, каким будет магнитное поле замкнутого контура. Например, можно вертикально ориентировать рамку в поле, силовые линии которого направлены сверху вниз.
Чтобы определить, какое направление будет иметь магнитная индукция в этой ситуации, следует также воспользоваться правилом левой руки. Так как ток в нижней части рамки направлен вправо, руку нужно расположить так, чтобы пальцы были направлены, если смотреть на рисунок, тоже вправо. При этом ладонь должна быть открыта вверх. Большой палец в такой ситуации будет направлен в сторону от наблюдателя.
Применив это правило для верхней части рамки, можно увидеть, что сила Ампера действует по направлению к наблюдателю. То есть, рамке придано вращательное движение. Однако по мере приближения к горизонтальному положению эта сила уменьшается.
Если рамка будет обладать инерцией и благодаря ей проскочит горизонтальное положение, то описанные выше силы вновь начнут действовать: вначале слабо, а затем будут увеличиваться по мере достижения рамкой вертикального положения.
Использование бесконечно малых величин
В указанных выше формулах применяются бесконечно малые величины (dF, dl). Их использование расширяет возможности расчёта параметров. Обычно экспериментально исследуются сравнительно простые ситуации, но при этом возникает необходимость получить формулы универсального характера.
В реальной жизни возможны, например, ситуации, когда напряжённость магнитного поля меняется по сложному закону или рассматриваются контуры проводников произвольной конфигурации.
Использование бесконечно малых величин даёт возможность обобщить результаты основополагающих экспериментов для самых разных ситуаций. Для этого могут быть применены методы дифференциального и интегрального исчисления.
При рассмотрении бесконечно малого участка провода речь идёт о величине, которая достаточно мала, чтобы считать её прямолинейной. В этом случае возможно применение уже существующих закономерностей. При помощи методов интегрирования можно перейти к проводам, которые имеют контур различной степени сложности или к рассмотрению магнитного поля сложной конфигурации.
Практическое применение
Сила Ампера используется практически во всех электромеханических устройствах, где необходимо с помощью электрических процессов вызвать движение реальных объектов. Одним из примеров применения являются измерительные приборы.
На рисунке приведен пример схемы измерительного прибора. К оси присоединен источник питания (4). Ось закреплена в подшипниках (5), поэтому может свободно вращаться. На оси есть прямоугольная рамка (1), через которую течёт ток. Она расположена между полюсами постоянного магнита (2). Контакты сделаны в виде спиральных пружин. К оси прикреплена стрелка (6), острие которой передвигается по шкале измерения (7).
При пропускании тока через проводник появляется магнитное взаимодействие, и рамка начинает вращаться. При этом смещается стрелка указателя до тех пор, пока сила Ампера не уравновесит силу упругости обеих пружин. Полученный показатель будет характеризовать ток, протекающий через проводник. Чем больше сила тока, тем сильнее отклонится стрелка.
На законе Ампера основывается и такая отрасль, как электротехника. Например, электромагнитная индукция применяется в электродвигателях.
Двигатель обеспечивает преобразование электроэнергии во вращение вала. Ток на рамку поступает через скользящие щётки. Она взаимодействует с постоянным магнитом, что приводит к её повороту под действием силы Ампера. В современных двигателях может использоваться одновременно несколько рамок. Это позволяет увеличить мощность мотора и сделать вращение оси более плавным.
Двигатели, работающие на основе рассматриваемого эффекта, активно используются в различных видах электротранспорта — трамваях, троллейбусах, электропоездах.
Еще одно применение закона Ампера — это громкоговорители. Внутри них находится постоянный магнит. Изменение силы тока вызывает изменение силы воздействия магнитного поля, что приводит к вибрации мембраны, производящей звук нужной частоты.
Притяжение между проводниками с током легло в основу точного определения единицы измерения 1 Ампер. При этом рассматривалась абстрактная ситуация, предполагающая наличие двух параллельно расположенных проводников с бесконечной длиной. Считалось, что каждый из них имеет бесконечно малое сечение, размерами которого можно пренебречь.
Принято, что на всём протяжении они находятся точно на расстоянии один метр и в вакууме. При прохождении тока величиной 1 Ампер сила, действующая на каждый метр проводников, должна составлять 0.0000002 Ньютона. Это определение вступило в силу в 1948 году.
Видео по теме
Гипотеза Ампера об элементарных электрических токах
Открытия Эрстеда и Ампера привели к новому и более глубокому представлению о природе магнитных явлении. Опираясь на установленную в этих опытах тождественность магнитных действий магнитов и соответствующим образом подобранных токов, Ампер решительно отказался от представления о существовании в природе особых магнитных зарядов. С точки зрения Ампера, элементарный магнит – это круговой ток, циркулирующий внутри небольшой частицы вещества: атома, молекулы или группы их. При намагничивании бóльшая или меньшая часть таких токов устанавливается параллельно друг другу, как показано на рис. 7.16, (амперовы токи).
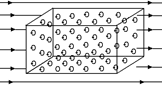 Рис. 7.16 Рис. 7.16 |
Мы видели, что по своим магнитным свойствам круговой ток вполне подобен короткому магниту, ось которого перпендикулярна к плоскости тока. Поэтому изображенная условно на рис. 7.16 система ориентированных молекулярных токов совершенно равносильна цепочкам элементарных магнитиков в гипотезе Кулона.
Таким образом, теория Ампера сделала ненужным допущение о существовании особых магнитных зарядов, позволив объяснить все магнитные явления при помощи элементарных электрических токов.
С точки зрения теории Ампера становится совершенно понятной неотделимость друг от друга северных и южных полюсов. Каждый элементарный магнит представляет собой круговой виток тока. Мы видели уже, что одна сторона этого витка соответствует северному, другая – южному полюсу. Именно поэтому нельзя отделить друг от друга северный и южный полюсы, как нельзя отделить одну сторону плоскости от другой.
Таким образом, мы пришли к следующему основному результату.
Никаких магнитных зарядов не существует. Каждый атом вещества можно рассматривать в отношении его магнитных свойств как круговой ток. Магнитное поле намагниченного тела слагается из магнитных полей этих круговых токов.
В ненамагниченном теле все элементарные токи расположены хаотически, и поэтому мы не наблюдаем во внешнем пространстве никакого магнитного поля.
Процесс намагничивания тела заключается в том, что под влиянием внешнего магнитного поля его элементарные токи в большей или меньшей степени устанавливаются параллельно друг другу и создают результирующее магнитное поле.
В чем заключается гипотеза ампера
Открытия Эрстеда и Ампера привели к новому и более глубокому представлению о природе магнитных явлений. Опираясь на установленную в этих опытах тождественность магнитных действий магнитов и соответствующим образом подобранных токов, Ампер решительно отказался от представления о существовании в природе особых магнитных зарядов. С точки зрения Ампера, элементарный магнит – это круговой ток, циркулирующий внутри небольшой частицы вещества: атома, молекулы или группы их. При намагничивании большая или меньшая часть таких токов устанавливается параллельно друг другу, как показано на рис. 209 (амперовы токи).
Рис. 209. Упорядоченное расположение амперовых токов в намагниченном железе, помещенном в магнитном поле
Мы видели в § 115, что по своим магнитным свойствам круговой ток вполне подобен короткому магниту, ось которого перпендикулярна к плоскости тока. Поэтому изображенная условно на рис. 209 система ориентированных молекулярных токов совершенно равносильна цепочкам элементарных магнитиков в гипотезе Кулона.
Таким образом, теория Ампера сделала ненужным допущение о существовании особых магнитных зарядов, позволив объяснить все магнитные явления при помощи элементарных электрических токов. Дальнейшее более глубокое изучение свойств намагничивающихся тел показало не только, что гипотеза магнитных зарядов или элементарных магнитиков излишня, но что она неверна и не может быть согласована с некоторыми экспериментальными фактами. Мы позже познакомимся с этими фактами (§ 147).
С точки зрения теории Ампера становится совершенно понятной неотделимость друг от друга северных и южных полюсов, о которой мы говорили в предыдущем параграфе. Каждый элементарный магнит представляет собой круговой виток тока. Мы видели уже, что одна сторона этого витка соответствует северному, другая – южному полюсу. Именно поэтому нельзя отделить друг от друга северный и южный полюсы, как нельзя отделить одну сторону плоскости от другой.
Таким образом, мы пришли к следующему основному результату.
Никаких магнитных зарядов не существует. Каждый атом вещества можно рассматривать в отношении его магнитных свойств как круговой ток. Магнитное поле намагниченного тела слагается из магнитных полей этих круговых токов.
В ненамагниченном теле все элементарные токи расположены хаотически, и поэтому мы не наблюдаем во внешнем пространстве никакого магнитного поля.
Процесс намагничивания тела заключается в том, что под влиянием внешнего магнитного поля его элементарные токи в большей или меньшей степени устанавливаются параллельно друг другу и создают результирующее магнитное поле.
Значение теории Ампера не вызывало сомнения. Однако представления Ампера о существовании элементарных токов, непрерывно циркулирующих внутри частиц веществ, были чрезвычайно смелы и необычны для его времени. Дальнейшее развитие науки сделало эти представления естественным следствием созданной в XX веке теории атома. Атом представляет собой систему из центрального положительно заряженного ядра и электронов, обращающихся около него, подобно тому как планеты обращаются вокруг Солнца. Движение электронов представляет собой круговые токи, циркулирующие внутри атомов. Удалось даже осуществить специальные опыты, показывающие, что намагничивание тел сопровождается ориентировкой осей этих круговых токов, стремящихся расположиться параллельно.
Такие наглядные представления о строении атомов являются слишком грубыми и потому неточными, однако они в общих чертах правильно передают сущность дела.
Магнитное поле. Источники. Гипотеза Ампера.
Гипотеза Ампера. Ампера (1775- 1836г.) выдвинул гипотезу о существовании электрических токов, циркулирующих внутри каждой молекулы вещества. В 1897г. гипотезу подтвердил английский учёный Томсон, а в 1910г. измерил токи американский учёный Милликен. Вывод: движение электронов представляет собой круговой ток, а о том, что вокруг проводника с электрическим током существует магнитное поле.
История магнетизма уходит корнями в глубокую древность, к античным цивилизациям Малой Азии. Именно на территории Малой Азии, в Магнезии, находили горную породу, образцы которой притягивались друг к другу. По названию местности такие образцы и стали называть «магнетиками». Любой магнит в форме стержня или подковы имеет два торца, которые называются полюсами; именно в этом месте сильнее всего и проявляются его магнитные свойства. Если подвесить магнит на нитке, один полюс всегда будет указывать на север. На этом принципе основан компас. Обращенный на север полюс свободно висящего магнита называется северным полюсом магнита (N). Противоположный полюс называется южным полюсом (S).
В 1820 г. Эрстед (1777-1851) обнаружил, что магнитная стрелка, расположенная рядом с электрическим проводником, отклоняется, когда по проводнику течет ток, т. е. вокруг проводника с током создается магнитное поле. Если взять рамку с током, то внешнее магнитное поле взаимодействует с магнитным полем рамки и оказывает на нее ориентирующее действие, т. е. существует такое положение рамки, при котором внешнее магнитное поле оказывает на нее максимальное вращающее действие, и существует положение, когда вращающий момент сил равен нулю.
Исто́чник то́ка (в теории электрических цепей) — элемент, двухполюсник, сила тока через который не зависит от напряжения на его зажимах (полюсах). Используются также термины генератор тока и идеальный источник тока.
Магнитная индукция.
Если заряд частицы равен q, ее скорость равна v, а индукция магнитного поля в данной точке пространства равна В, то на частицу в данной точке со стороны магнитного поля действует сила, равная:
Таким образом, В — это вектор, величина и направление которого таковы, что сила Лоренца, действующая на движущийся заряд со стороны магнитного поля равна:
Здесь альфа — это угол между вектором скорости и вектором магнитной индукции. Вектор силы Лоренца F перпендикулярен вектору скорости и вектору магнитной индукции. Его направление для случая движения положительно заряженной частицы в однородном магнитном поле определяется правилом левой руки:

Поскольку ток в проводнике является движением заряженных частиц, то магнитную индукцию можно определить и как отношение максимального механического момента, действующего со стороны однородного магнитного поля на рамку с током, к произведению силы тока в рамке на площадь рамки:
Магнитная индукция — фундаментальная характеристика магнитного поля, как напряженность для электрического поля. В системе СИ магнитная индукция измеряется в тесла (Тл), в системе СГС — в гауссах (Гс). 1 тесла = 10000 гаусс. 1 Тл — это индукция такого однородного магнитного поля, в котором на рамку площадью 1 м2, по которой течет ток в 1 А, действует максимальный вращающий механический момент сил, равный 1 Н • м.
Кстати, индукция магнитного поля Земли на широте 50° в среднем составляет 0,00005 Тл, а на экваторе — 0,000031 Тл. Вектор магнитной индукции всегда направлен по касательной к магнитной силовой линии.
Магнитные силы.
Магнитное поле действует получила название – сила Сила, действующая на проводник тока, длине проводника, магнитной направлением вектора магнитной определить по правилу левой движущиеся заряды широко циклотроне- ускорителе элементарных Хорошо известно, что магнитное постоянными магнитами. Постоянные веществ, но все вещества создают магнитное поле. Согласно микроскопическими токами Закон Фарадея, основной закон э.д.с. индукции в проводнике пересекает магнитные силовые Если замкнутый проводник изменяющемся магнитном проводника в магнитном поле создавая на другом конце проводника проводника возникает разность только тогда, когда проводник проводник удаляют из магнитного Электромагнитная проводник когда Напряжение индуцированным э.д которой углом поля больше перемещается Относительное возникать вследствие перемещения поля или и того, и другого перемещается под прямым углах меньших 90 градусов перемещается параллельно проводник, тем больше индуцированное действует с определенной силой на проводник с током сила Ампера.
на проводник, по которому течет ток, прямо пропорциональна проводника, магнитной индукции и синусу угла между направлением вектора магнитной индукции. Направление силы Ампера правилу левой руки. Кроме этого, магнитное поле действует частицу, находящуюся в магнитном поле называют силой Лоренца. Силу Лоренца можно определить по формуле :
На движущуюся частицу со стороны магнитного действует сила Лоренца, которая перпендикулярна и не совершает работы. Действие магнитного широко используется в современной технике, например ускорителе элементарных частиц. магнитное поле создается ни только электрическими магнитами. Постоянные магниты могут быть изготовлены вещества, помещенные в магнитное поле, намагничиваются поле. Согласно гипотезе Ампера эти поля порождаются токами, циркулирующими внутри атомов и молекул основной закон электромагнетизма, формулируется проводнике прямо пропорциональна скорости, с которой магнитные силовые линии, т.е. скорости изменения магнитного проводник перемещается в магнитном поле или находится магнитном поле, то в нем возникает электрический ток итном поле электроны перемещаются к одному концу конце проводника дефицит электронов. В результате возникает разность потенциалов. Эта разность потенциалов проводник перемещается относительно магнитного из магнитного поля, свободные электроны возвращаются Электромагнитная индукция имеет место в двух проводник перемещается относительно магнитного когда магнитное поле перемещается относительно апряжение, возникающее в проводнике, называется индуцированным напряжением, или э.д.с индукции э.д.с. определяется величиной магнитного поля которой проводник перемещается относительно углом, под которым находится проводник относительно поля, и длиной проводника. Чем сильнее магнитное больше величина э.д.с. индукции.
Чем быстре перемещается относительно поля, тем больше Относительное движение проводника и магнитного перемещения проводника (но не вдоль самого другого. Максимальное напряжение индуцируется прямым углом по отношению к силовым линиям магнитного градусов индуцируется меньшее напряжение. Если параллельно силовым линиям, э.д.с. индукции не возникает больше индуцированное напряжение.
Магнитные свойства веществ.
Всякое вещество является магнетиком, т.е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться). По величине и направлению этого момента, а также по причинам, его породившим, все вещества делятся на группы. Основные из них – диа- и парамагнетики.
Молекулы диамагнетика собственного магнитного момента не имеют. Он возникает у них только под действием внешнего магнитного поля и направлен против него. Таким образом, результирующее магнитное поле в диамагнетике меньше, чем внешнее поле, правда, на очень малую величину. Это приводит к тому, что при помещении диамагнетика в неоднородное магнитное поле он стремится сместиться в ту область, где напряжение магнитного поля меньше.
Существует ряд веществ, в которых квантовые эффекты межатомных взаимодействий приводят к появлению специфических магнитных свойств.
Естественно, что ферромагнетики, как и парамагнетики, перемещаются в ту точку поля, где напряженность максимальная (втягиваются в магнитное поле). Из-за большой величины магнитной проницаемости сила, действующая на них, гораздо больше.
При понижении температуры все парамагнетики, кроме тех, у которых парамагнетизм обусловлен электронами проводимости, переходят либо в ферромагнитное, либо в антиферромагнитное состояние.
Для антиферромагнетиков также существует температура, при которой антипараллельная ориентация спинов исчезает. Эта температура называется антиферромагнитной точкой Кюри или точкой Нееля.
У некоторых ферромагнетиков (эрбин, диоброзин, сплавов марганца и меди) таких температур две (верхняя и нижняя точка Нееля), причем антиферромагнитные свойства наблюдаются только при промежуточных температурах. Выше верхней точки вещество ведет себя как парамагнетик, а при температурах, меньших нижней точки Нееля, становится ферромагнетиком.
Суперпарамагнетизм— квазипарамагнитное поведение систем, состоящих из совокупности экстремально малых ферро- или ферримагнитных частиц. Частицы этих веществ при определенно малых размерах переходят в однодоменное состояние с однородной самопроизвольной намагниченностью по всему объему частицы. Совокупность таких веществ ведет себя по отношению к воздействию внешнего магнитного поля и температуры подобно парамагнитному газу (сплавы меди с кобальтом, тонкие порошки никеля и т.д.).
Суперпарамагнетизмприменяется в тонких структурных исследованиях, в методах неразрушающего определения размеров, форм, количества и состава магнитной фазы и т.п.
Пьезомагнетики— вещества, у которых при наложении упругих напряжений возникает спонтанный магнитный эффект, пропорциональный первой степени величины напряжений. Этот эффект весьма мал и легче всего его обнаружить в антиферромагнетиках.
21) Гармонические колебания. Условия, характеристики, уравнение, графики.
Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд; 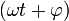

Обобщенное гармоническое колебание в дифференциальном виде:
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.































