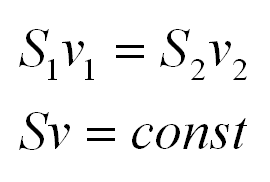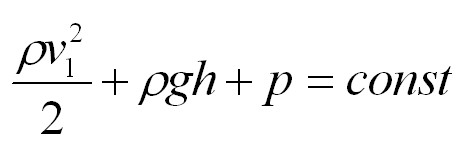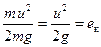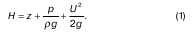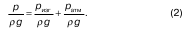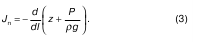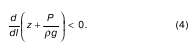в чем заключается геометрический смысл уравнения бернулли

Уравнение Бернулли

Уравнение Бернулли для потока идеальной жидкости

Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении.

Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.

Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим:

Физический смысл уравнения Бернулли

Составляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости:

Физический и энергетический смысл уравнения Бернулли заключается в постоянстве полной удельной энергии вдоль элементарной струйки идеальной жидкости.

Уравнение Бернулли отражает закон сохранения механической энергии для идеальной несжимаемой жидкости.

Уравнение Бернулли для потока реальной вязкой жидкости

Если на участке между расчетными сечениями не совершается механическая работа, а движение является установившимся, без притока и отбора жидкости, и сама жидкость является несжимаемой, то для потока будут справедливы зависимости:

Иллюстрация уравнения Бернулли

Для иллюстрации закона Бернулли на координатной плоскости, совмещенной с принципиальной гидравлической схемой системы изображают напорную и пьезометрическую линии.

Уравнение Бернулли для горизонтальной трубы

Для горизонтальных трубопроводов и силовых гидроприоводов, в которых пьезометрический набор существенно превышает геометрический удобна следующая форма записи уравнения Бернулли:

Алгоритм решения задач с помощью уравнения Бернулли

Задачи с помощью уровнения Бернулли удобно решать в следующей последовательности:

Источник

Течение жидкости и уравнение Бернулли для новичков

Как закон Всемирного Тяготения Ньютона действовал задолго до самого Ньютона, так и уравнение Бернулли существовало задолго до того, как родился сам Бернулли. Ему удалось лишь облечь это уравнение в наглядную форму, в чем его неоспоримая и огромная заслуга. Зачем мне уравнение Бернулли, спросите Вы, ведь я прекрасно жил и без него. Да, но оно может пригодиться Вам хотя бы на экзамене по гидравлике! Как говорится, «все не так уж плохо, если ты знаешь и можешь сформулировать уравнение Бернулли».

Кто такой Бернулли?

Даниил Бернулли – сын известного ученого Якоба Бернулли, швейцарский математик и физик. Жил с 1700 по 1782 годы, а с 1725 по 1733 трудился в Петербургской Академии наук. Помимо физики и математики Бернулли также изучал медицину наряду с Д’Аламбером и Эйлером считается отцом основателем математической физики. Успехи этого человека позволяют с уверенностью сказать, что это был настоящий «супермозг».

Д. Бернулли (1700-1782)

Идеальная жидкость и течение идеальной жидкости

Помимо известной нам материальной точки и идеального газа существует также идеальная жидкость. Какой-нибудь студент, конечно, может подумать, что эта жидкость – его любимое пиво или кофе, без которого невозможно жить. Но нет, идеальная жидкость – это жидкость, которая абсолютно несжимаема, лишена вязкости и теплопроводности. Тем не менее, такая идеализация дает вполне хорошее описание движения реальных жидкостей в гидродинамике.

Течением жидкости называется движение ее слоев относительно друг друга или относительно всей жидкости.

Помимо того есть разные режимы течения жидкости. Нас интересует тот случай, когда скорость потока в какой-то конкретной точке не меняется со временем. Такой поток называют стационарным. При этом скорость течения в различных точках стационарного потока может различаться.

Поток жидкости– совокупность частиц движущейся жидкости.

Поток жидкости

Вывод уравнения Бернулли

Но как описать движение жидкости? Для этого нам нужно знать вектор скорости частиц, точнее зависимость его от времени. Совокупность скоростей в разных точках потока дает поле вектора скорости.

Рассмотрим стационарное течение жидкости по трубке. В одном месте сечение этой трубки равно S1, а в другой – S2. При стационарном потоке через оба сечения за одинаковый промежуток времени пройдет одинаковое количество жидкости.

Данное уравнение – уравнение неразрывности струи.

К выводу уравнения Бернулли

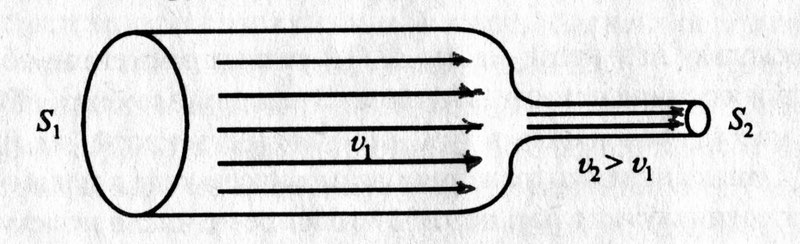
Узнав его, Бернулли решил установить связь между давлением и скоростью жидкости в разных сечениях. Полное давление – это сумма статистического (обусловлено потенциальной энергией жидкости) и динамического давлений (обусловлено кинетической энергией). Оказывается, сумма статического и динамического давлений в любом сечении трубы постоянна. Само же уравнение Бернулли имеет вид:

Смысл уравнения Бернулли

Физический смысл уравнения Бернулли. Уравнение Бернулли является следствием закона сохранения энергии. Первый член уравнения Бернулли – это кинетическая энергия, второе слагаемое уравнения Бернулли – потенциальная энергия в поле силы тяжести, третье – работа силы давления при подъеме жидкости на высоту h.

Вот и все, друзья, не так уж и страшно. Совсем немного времени, а Вы уже знаете уравнение Бернулли. Даже если Вы не знаете больше ничего, с этими знаниями идти на экзамен или зачет гораздо лучше, чем просто так. А если Вам необходима помощь в том, как решать задачи на уравнение Бернулли – не стесняйтесь и оформляйте заявку. После того как наши авторы распишут решение уравнения Бернулли максимально подробно, у Вас не останется пробелов в знаниях.

Источник

Геометрический и энергетический смысл уравнения Бернулли для струйки

Поскольку все члены уравнений (3.22) и (3.23) имеют размерность длины, они могут быть легко проиллюстрированы гео­метрически.

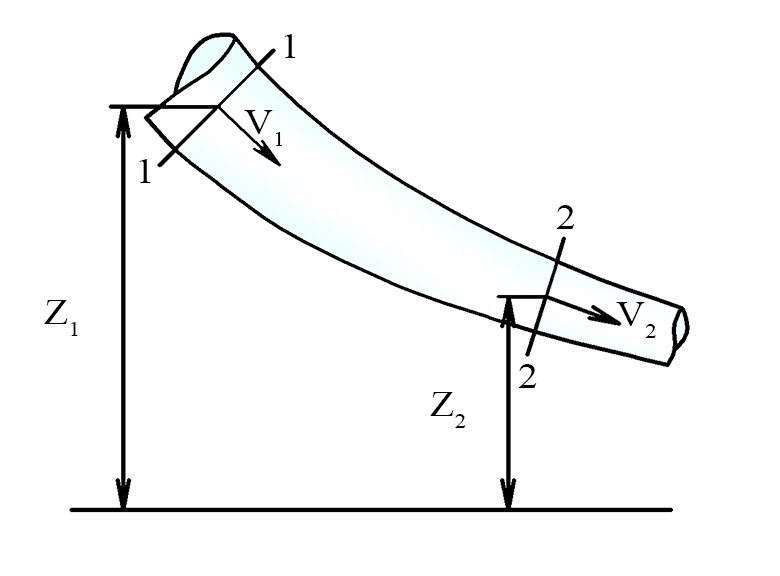
Изобразим элементарную струйку и выделим в ней два сечения (рис. 3.4).

Ось трубки является линией тока и траекторией при установившемся движении.

Геометрический и энергетический смысл членов z и р/γрассмотрены в гидростатике.

В каждой точке линии тока отложим вверх пьезометрические высоты. Соединив концы отрезков, изображающих эти высоты, плав­ной кривой, получим линию, называемую пьезометрической. Одновременно эта линия изображает изменение гидростатического напора z + р/γ.

Третий член уравнения Бернулли имеет размерность длины.

Величину u 2 /2g называют скоростной высотой или скоростным напо­ром.

Отложим эти отрезки вверх от пьезометрической ли­нии.

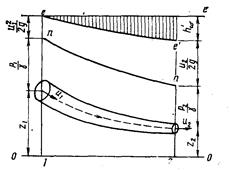
Рис. 3.4. Геометрическая и энергети­ческая интерпретация уравнения Бернулли для струйки вязкой жид­кости

Сумма пьезометрического и скоростного напоров представ­ляет собой полный напор, называемый гидродинамическим напором. Различают гидродинамический напор при абсолютном давлении и избыточном (избыточный гидродинамический напор).

Геометрический смысл уравнения Бернулли для струйки невяз­кой жидкости состоит в том, что гидродинамический напор остается постоянным по длине струйки.

Кинетичес­кая энергия частицы, имеющей массу т, равна т и 2 /2. Отнеся её к единице веса, т. е. тg, получим:

Кинематическая энергия частицы жидкости, отнесенная к единице её веса, количественно равная е_к, называется удельной кинетической энергией частицы.

Энергия движущейся частицы жидкости, отнесен­ная к единице её веса и условной горизонтальной плоскости, количест­венно равная е = е_п + е_к, называется удельной энергией частицы, где е_п — удельная потенциальная энергия частицы.

Поскольку удельная энергия выражается в единицах длины, то пол­ная удельная энергия е равна гидродинамическому напору.

Геометри­ческий смысл уравнения Бернулли для струйки вязкой жидкости: сумма геометрической, пьезометрической и ско­ростной высот уменьшается вниз по течению.

Линию, характеризующую изменение пьезометрического напора по длине струй­ки, называют пьезометрической линией п — п(см. рис. 3.4).

Если представить себе пьезометры, установленные вдоль струйки, то пьезо­метрическая линия пройдет по горизонтам жидкости в пьезометрах.

Пьезометрическая линия может не только понижаться, но и повышать­ся, если площадь живого сечения струйки увеличивается. Линию, характеризующую изменение гидродинамического напора по длине струйки, называют линией гидродинамического напора, или напорной линией е — е’.

Эта линия может только понижаться.

Чтобы построить напорную линию, необходимо измерить скоростные высоты (напоры).

Напорная линия возвышается над пьезометрической на величину е_к = u 2 /2g.

На рис. 3.4 показана вертикальной штриховкой эпюра изменения удельной энергии, потерянной на сопротивление движе­нию. В сечении 2она равна h′_ω.

Источник

30. Геометрический смысл уравнения Бернулли

30. Геометрический смысл уравнения Бернулли

Основу теоретической части такой интерпретации составляет гидравлическое понятие напор, которое принято обозначать буквой Н, где

Гидродинамический напор Н состоит из следующих разновидностей напоров, которые входят в формулу (198) как слагаемые:

2) U 2 /2g – скоростной напор.

Все слагаемые имеют линейную размерность, их можно считать высотами. Назовем эти высоты:

1) z – геометрическая высота, или высота по положению;

2) p/?g – высота, соответствующая давлению p;

3) U 2 /2g – скоростная высота, соответствующая скорости.

Геометрическое место концов высоты Н соответствует некоторой горизонтальной линии, которую принято называть напорной линией или линией удельной энергии.

Точно так же (по аналогии) геометрические места концов пьезометрического напора принято называть пьезометрической линией. Напорная и пьезометрическая линии расположены друг от друга на расстоянии (высоте) p атм/?g, поскольку p = p изг + pат, т. е.

Отметим, что горизонтальная плоскость, содержащая напорную линию и находящаяся над плоскостью сравнения, называется напорной плоскостью. Характеристику плоскости при разных движениях называют пьезометрическим уклоном J п, который показывает, как изменяется на единице длины пьезометрический напор (или пьезометрическая линия):

Пьезометрический уклон считается положительным, если он по течению струйки (или потока) уменьшается, отсюда и знак минус в формуле (3) перед дифференциалом. Чтобы J п остался положительным, должно выполняться условие

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

7. Анализ основного уравнения гидростатики

22. Дифференциальные уравнения движения невязкой жидкости

22. Дифференциальные уравнения движения невязкой жидкости Уравнение Эйлера служит одним из фундаментальных в гидравлике, наряду с уравнением Бернулли и некоторыми другими.Изучение гидравлики как таковой практически начинается с уравнения Эйлера, которое служит

24. Форма Громеки уравнения движения невязкой жидкости

24. Форма Громеки уравнения движения невязкой жидкости Уравнения Громеки – попросту другая, несколько преобразованная форма записи уравнения Эйлера.Например, для координаты x Чтобы его преобразовать, используют уравнения компонентов угловой скорости для вихревого

25. Уравнение Бернулли

26. Анализ уравнения Бернулли

26. Анализ уравнения Бернулли это уравнение есть не что иное, как уравнение линии тока при установившемся движении.Отсюда следуют выводы:1) если движение установившееся, то первая и третья строки в уравнении Бернулли пропорциональны.2) пропорциональны строки 1 и 2,

27. Примеры прикладного применения уравнения Бернулли

27. Примеры прикладного применения уравнения Бернулли Во всех случаях требуется определить математическую формулу потенциальной функции, которая входит в уравнение Бернулли: но эта функция имеет разные формулы в разных ситуациях. Ее вид зависит от того, какие массовые

29. Энергетический смысл уравнения Бернулли

29. Энергетический смысл уравнения Бернулли Пусть теперь имеем установившееся движение жидкости, которая невязкая, несжимаемая.И пусть она находится под воздействием сил тяжести и давления, тогда уравнение Бернулли имеет вид: Теперь требуется идентифицировать каждое

31. Уравнения движения вязкой жидкости

31. Уравнения движения вязкой жидкости Для получения уравнения движения вязкой жидкости рассмотрим такой же объем жидкости dV = dxdydz, который принадлежит вязкой жидкости (рис. 1).Грани этого объема обозначим как 1, 2, 3, 4, 5, 6. Рис. 1. Силы, действующие на элементарный объем

33. Уравнение Бернулли для движения вязкой жидкости

33. Уравнение Бернулли для движения вязкой жидкости Элементарная струйка при установившемся движении вязкой жидкостиУравнение для этого случая имеет вид (приводим его без вывода, поскольку его вывод сопряжен с применением некоторых операций, приведение которых

35. Уравнение Бернулли для неустановившегося движения вязкой жидкости

35. Уравнение Бернулли для неустановившегося движения вязкой жидкости Для того, чтобы получить уравнение Бернулли, придется определить его для элементарной струйки при неустановившемся движении вязкой жидкости, а затем распространять его на весь потокПрежде всего,

53. Дифференциальные уравнения неустановившегося движения

53. Дифференциальные уравнения неустановившегося движения Для того, чтобы составить уравнение любого вида движения, нужно проецировать все действующие силы на систему и приравнивать их сумму к нулю. Так и поступим.Пусть имеем напорный трубопровод круглого сечения, в

39. Принцип возрастания энтропии и физический смысл второго закона термодинамики

39. Принцип возрастания энтропии и физический смысл второго закона термодинамики Исследуем понятие энтропии как функции состояния: Второй закон термодинамики можно сформу лировать в виде: Величина энтропии представляет собой полный диффереренциал, т. е. является

46. Основные дифференциальные уравнения термодинамики

46. Основные дифференциальные уравнения термодинамики Дифференциальные уравнения в термодинамике используются для исследования реальных газов, при теоретических (и практических) вычислениях.Рассмотрим следующие случаи.1. Независимыми переменными являются параметры p,

13.4. Философский смысл торговли и дарвинизм

13.4. Философский смысл торговли и дарвинизм Принципы рыночной экономики и международной торговли своими философскими корнями восходят к работе Адама Смита «Богатство народов» и к концепциям Давида Рикардо о специализации и конкурентных преимуществах народов. Их теория

Источник

ФИЗИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ УРАВНЕНИЯ БЕРНУЛЛИ. НАПОР ЖИДКОСТИ

Уравнению Бернулли можно дать два различных истолкования: физическое и геометрическое.

С физической точки зрения уравнение Бернулли есть выражение закона сохранения энергии для движущейся жидкости.

Действительно, рассмотрим величину

.

Эта сумма 3-х слагаемых называется полным напором жидкости или гидродинамическим напором.

С физической точки зрения напор есть механическая энергия жидкости, отнесенная к единице веса жидкости. Для того чтобы это показать, рассмотрим жидкость, движущуюся по трубопроводу (рис.4.16). Выделим в движущейся жидкости частицу M с массой m, веса . Потенциальная энергия этой частицы в поле силы тяжести по отношению к плоскости сравнения 0-0 будет mgz, а потенциальная энергия, отнесенная к единице веса, будет

,

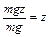
Под действием давления p частица жидкости М может подняться на высоту и, следовательно, совершить работу (рис.4.17)

,

т.е. она обладает потенциальной энергией давления в размере

.

Потенциальная энергия давления, отнесенная к единице веса, будет

,

т.е. — есть удельная потенциальная энергия давления частицы жидкости – энергия, отнесенная к единице веса жидкости.

Кроме того, выделенная частица обладает скоростью и, следовательно, имеет кинетическую энергию, равную .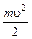

Кинетическая энергия, отнесенная к единице веса, будет

.

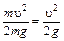
будет, следовательно, равен полной энергии частицы жидкости, отнесенной к единице веса.

Таким образом, физическое истолкование уравнения Бернулли для элементарной струйки идеальной жидкости заключается в том, что для любых сечений 1 и 2 полная удельная энергия остается неизменной:

.

Уравнению Бернулли можно дать наглядное геометрическое истолкование. Для этого снова рассмотрим отдельные члены суммы

,

где z – геометрическая высота данной частицы жидкости над условной плоскостью сравнения.

— пьезометрическая высота – высота, на которую поднимется жидкость в пьезометре.

Таким образом, с геометрической точки зрения уравнение Бернулли в любом сечении элементарной струйки идеальной жидкости представляет собой сумму 3-х высот: геометрической, пьезометрической и скоростной, которая остается неизменной.

График уравнения Бернулли для элементарной струйки идеальной жидкости представлен на рис. 4.18.

Если сечение струйки увеличивается, то скорость падает, а давление возрастает, т.е. энергия, сохраняясь в целом, переходит из одного вида в другой (кинетическая энергия переходит в потенциальную и наоборот).

§ 4.11. УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ЭЛЕМЕНТАРНОЙ
СТРУЙКИ РЕАЛЬНОЙ ЖИДКОСТИ

В идеальной жидкости, в отличие от реальной, отсутствуют силы внутреннего трения (отсутствует вязкость). Благодаря вязкости в реальной жидкости происходят потери механической энергии потока на трение внутри жидкости и о стенки канала. При этом происходит рассеивание (диссипация) энергии. Энергия, потерянная на трение, превращается в теплоту и идет на пополнение запаса внутренней энергии жидкости, а часть ее отводится в виде тепла через стенки канала.

Внутренняя энергия жидкости не может быть непосредственно использована для приведения жидкости в движение и поэтому в гидравлике рассматривается как потеря механической энергии (потеря напора).

Для реальной жидкости равенство нарушается и вместо него имеем , где – потеря напора на участке 1-2. Тогда для элементарной струйки реальной жидкости уравнение Бернулли примет вид

.

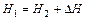
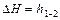
Таким образом, полный напор вдоль струйки реальной жидкости уменьшается. Для характеристики относительного изменения полного напора на единицу длины вводится понятие о гидравлическом уклоне

.

Например, на прямом участке трубопровода 1-2

,

Таким образом, гидравлическим уклоном называется отношение потери напора к длине, на которой она происходит.

Кроме того вводится еще понятие о пьезометрическом уклоне

.

Пьезометрический уклон может быть положительным, равным нулю и отрицательным.

Дата добавления: 2015-04-18 ; просмотров: 629 ; Нарушение авторских прав

Источник