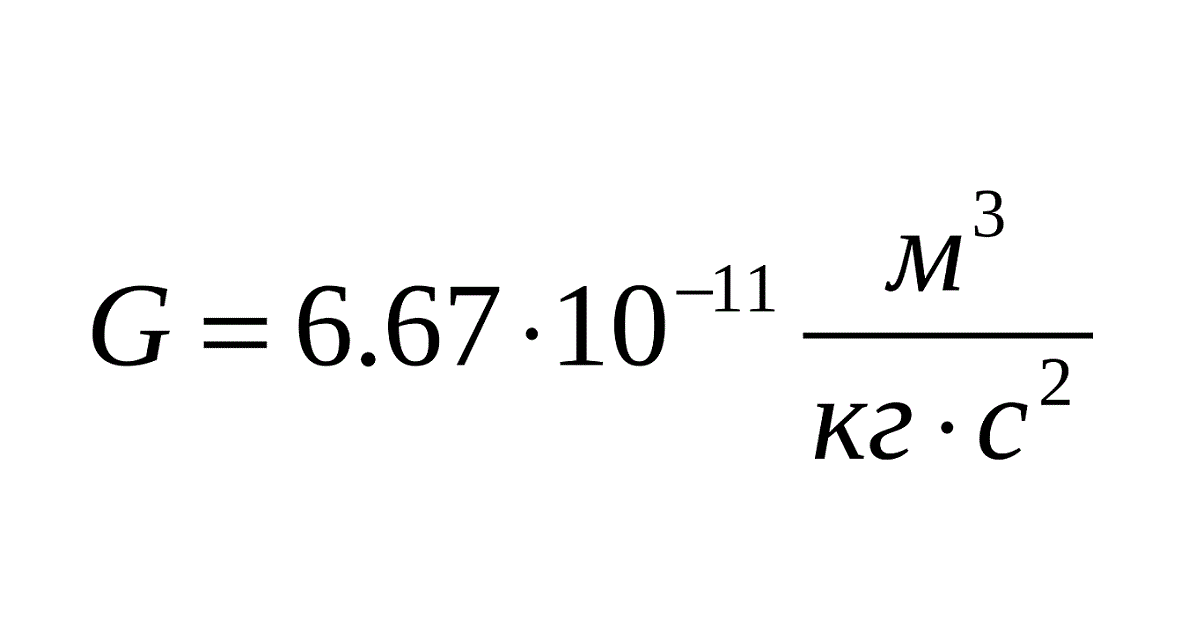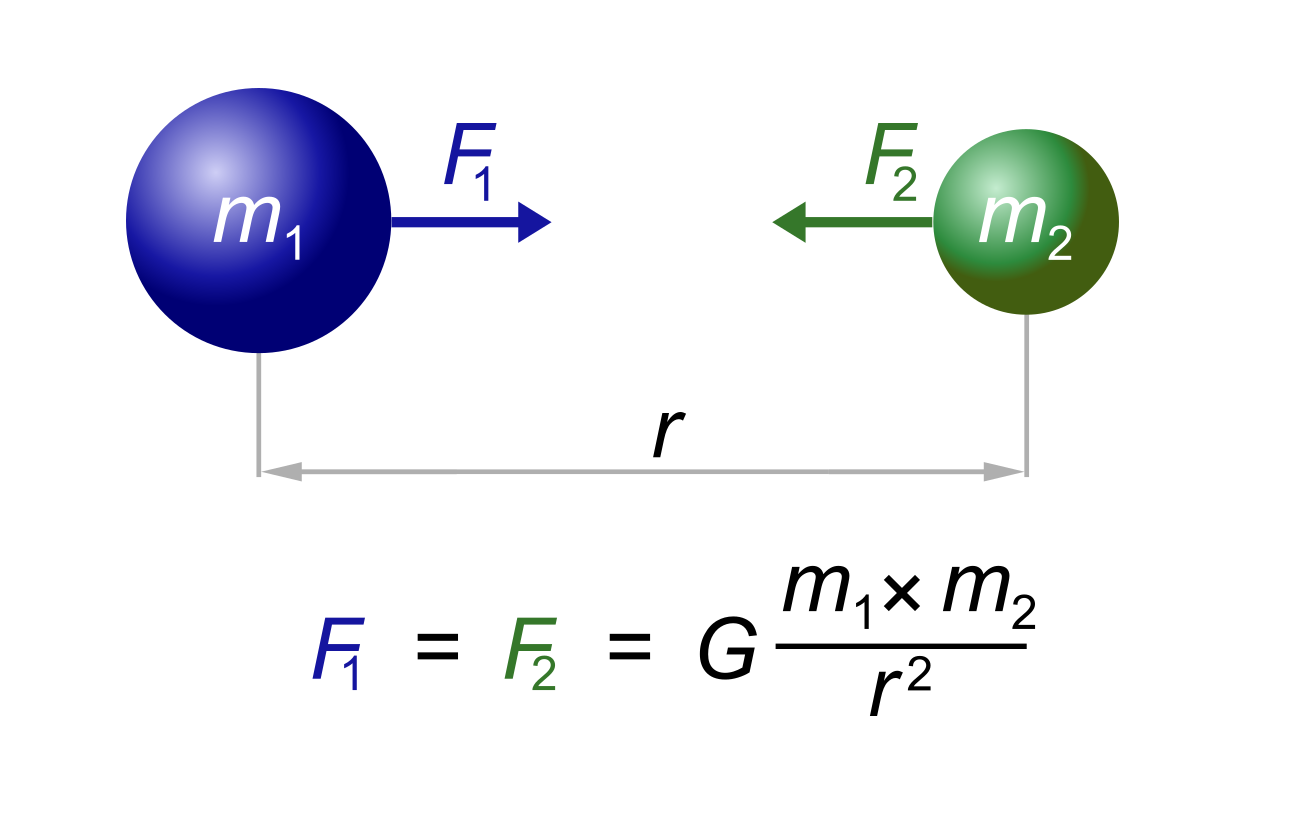в чем заключается физический смысл гравитационной постоянной
Гравитационная постоянная
Значение гравитационной постоянной
Общие сведения
Гравитационная постоянная или иначе – постоянная Ньютона – одна из основных констант, используемых в астрофизике. Фундаментальная физическая постоянная определяет силу гравитационного взаимодействия. Как известно, силу, с которой каждое из двух тел, взаимодействующих посредством гравитации, притягивается можно высчитать из современной формы записи закона всемирного тяготения Ньютона:
Гравитационное взаимодействие двух тел
Данный коэффициент пропорциональности равен модулю силы тяготения первого тела, которая действует на точечное второе тело единичной массы, при единичном расстоянии между этими телами.
Очевидно, что данная формула широко применима в области астрофизики и позволяет рассчитать гравитационное возмущение двух массивных космических тел, для определения дальнейшего их поведения.
Работы Ньютона
Примечательно, что в трудах Ньютона (1684—1686) гравитационная постоянная в явном виде отсутствовала, как и в записях других ученых аж до конца XVIII-го века.
Исаак Ньютон (1643 — 1727)
Ранее использовался так называемый гравитационный параметр, который равнялся произведению гравитационной постоянной на массу тела. Нахождение такого параметра в то время было более доступно, поэтому на сегодняшний день значение гравитационного параметра различных космических тел (в основном Солнечной системы) более точно известно, нежели порознь значение гравитационной постоянной и массы тела.
Здесь: µ — гравитационный параметр, G – гравитационная постоянная, а M — масса объекта.
Следует отметить тот факт, что значение гравитационной постоянной несколько варьируется даже до сегодняшнего дня, а чистое значение масс космических тел в то время было определить довольно сложно, поэтому гравитационный параметр нашел более широкое применение.
Эксперимент Кавендиша
Эксперимент по определению точного значения гравитационной постоянной впервые предложил английский естествоиспытатель Джон Мичелл, который сконструировал крутильные весы. Однако, не успев провести эксперимент, в 1793-м году Джон Мичелл умер, а его установка перешла в руки Генри Кавендишу – британскому физику. Генри Кавендиш улучшил полученное устройство и провел опыты, результаты которых были опубликованы в 1798-м году в научном журнале под названием «Философские труды Королевского общества».
Генри Кавендиш (1731 — 1810)
Установка для проведения эксперимента состояла из нескольких элементов. Прежде всего она включала 1,8-метровое коромысло, к концам которого крепились свинцовые шарики с массой 775 г и диаметром 5 см. Коромысло было подвешено на медной 1-метровой нити. Несколько выше крепления нити, ровно над ее осью вращения устанавливалась еще одна поворотная штанга, к концам которой жестко крепились два шара массой 49,5 кг и диаметром 20 см. Центры всех четырех шаров должны были лежать в одной плоскости. В результате гравитационного взаимодействия притяжение малых шаров к большим должно быть заметно. При таком притяжении нить коромысла закручивается до некоторого момента, и ее сила упругости должна равняться силе тяготения шаров. Генри Кавендиш измерял силу тяготения посредством измерения угла отклонения плеча коромысла.
Установка Генри Кавендиша
Более наглядное описание эксперимента доступно в видео ниже:
Для получения точного значения константы Кавендишу пришлось прибегнуть к ряду мер, снижающих влияние сторонних физических факторов на точность эксперимента. В действительности Генри Кавендиша проводил эксперимент не для того, чтобы выяснить значение гравитационной постоянной, а для расчета средней плотности Земли. Для этого он сравнивал колебания тела, вызванные гравитационным возмущением шара известной массы, и колебания, вызванные тяготением Земли. Он достаточно точно вычислил значение плотности Земли – 5,47 г/см 3 (сегодня более точные расчеты дают 5,52 г/см 3 ). Согласно различным источникам, значение гравитационной постоянной, высчитанное из гравитационного параметра с учетом плотности Земли, полученной Кавердишем, составило G=6,754·10 −11 м³/(кг·с²), G = 6,71·10 −11 м³/(кг·с²) или G = (6,6 ± 0,04)·10 −11 м³/(кг·с²). До сих пор неизвестно, кто впервые получил численное значение постоянной Ньютона из работ Генри Кавердиша.
Измерение гравитационной постоянной
Наиболее раннее упоминание гравитационной постоянной, как отдельной константы, определяющей гравитационное взаимодействие, найдено в «Трактате по механике», написанном в 1811-м году французским физиком и математиком — Симеоном Дени Пуассоном.
Материалы по теме
Гравитационные волны
Похожие статьи
Понравилась запись? Расскажи о ней друзьям!
Физический смысл гравитационной постоянной
Руководитель группы учёных из Международного Бюро Мер и Весов жалуется: «Существует фундаментальная физическая константа, точное значение которой до сих пор не выяснено, а это метрологический и научный тупик. И метрологи ломают копья в постоянных битвах за вычисление точной величины гравитационной постоянной..»
4. Каждое тело притягивает к себе. Если между ними ОДНА сила притяжения, тогда результатом будет разность этих сил, но не сила притяжения одного тела другим. Следовательно, тела притягиваются ДВУМЯ силами, равными по модулю, Но в таком случае бОльшее по массе тело каким-то образом дополняет силу меньшего по массе своей.
5. Исследователей всегда удивлял тот факт, что в афелии (т.е. на максимальном удалении от Солнца) планета может и имеет(а может быть и имеет) перевес центробежной силы над центростремительной, но почему-то планета не уходит в «никуда», а продолжает движение, «возвращаясь» по своей орбите? Так какой же силой она возвращается? Настоящие физики могут объяснить даже необъяснимое, привлекая математику, поэтому они ввели добавочную силу, представляющую собой равнодействующую проекций векторов переносного и относительного движений на плоскость абсолютного движения, и нормальная составляющая переносного ускорения должна «выдать» эту добавочную силу. Понятно? Мне тоже.
Считаем, что на самом деле, никакой добавочной силы нет, а есть взаимосвязанный процесс втягивания(притяжения) гравитационной силой этой планеты в направлении от Солнца к себе в каждый данный момент и выталкивания своей же инертной массы в противоположном (к Солнцу)направлении высвобожденной инерциальной силой инертной массы планеты. И эта сила на многие порядки больше своей силы притяжения, достигшей Солнца, т.к. инертная масса планеты в этом направлении осталась неуравновешенной своей гравитационной силой.
И.Ньютон писал:»Силы, которыми главные планеты постоянно отклоняются от прямолинейного движения и удерживаются на своих орбитах, НАПРАВЛЕНЫ(выделено мной) к Солнцу и обратно пропорциональны квадратам расстояния до его центра»
Считается, что гравитационная постоянная G была введена Пуассоном в уже существующую формулу всемирного тяготения спустя более чем столетие после опубликования трудов Ньютона в связи с переходом к единой метрической системе мер. Т.е. была введена волевым решением в качестве коэффициента пропорциональности, и уже исходя из размерности величин, входящихв формулу, определили её размерность. Численное значение G было получено на основе значения средней плотности Земли, вычисленной Кавендишем.
Чтобы уравновесить силу притяжения между свинцовым и ртутным шарами, нужно положить гирьку 0,7мг, что даёт силу притяжения Fпр.= 6,7388х10^-6н. Если два тела различной массы воздействуют друг на друга одинаковой силой, то логично предположить, что сила F каждого тела обратно пропорциональна их массам.
На основании исходных данных и нашего предположения составляем равенство для силы каждого шара:
Fпр.св.= 6,7388х10^-6н = Gсв./r^2 х Mрт./Mсв.= Fвт.св.х Mрт./Мсв.
Fпр.рт.= 6,7388х10^-6н = Gрт./r^2 х Мсв./Мрт.= Fвт.рт.х Мсв./Мрт. где
Сила притяжения известна из опыта, массы шаров, их радиусы и расстояние между ними известны, вычисляем неизвестные величины:
Gсв. = 2,40172х10^-3 кгм^3/c^2 Gрт. = 1,668х10^-9 кгм^3/c^2
Определяем гравитационные втягивающие силы шаров:
Fвт.св. = Gсв./r^2 = 8,0866х10^-3 н
Fвт.рт. = Gрт./r^2 = 5,6157х10^-9 н
Отсюда уже можно сделать вывод, что сила притяжения свинцового шара является частью его гравитационной втягивающей силы, а гравитационная втягивающая сила ртутного шара является лишь частью своей силы притяжения. Масса свинцового шара больше массы ртутного в 1,2х10^3 раз, а его гравитационная втягивающая сила больше такой же у ртутного в 1,44х10^6 раз, следовательно, при арифметическом росте массы её гравитационная сила растёт геометрически.
Отношение гравитационных втягивающих сил шаров равно квадрату отношения их масс:
Fвт.св./Fвт.рт. = 1,44х10^6 (Mсв./Mрт.)^2 = 1,44х10^6
Следовательно, для нахождения гравитационного эквивалента для любой другой массы, нужно отношение величины этой массы к величине одной из опытных масс возвести в квадрат, и умножить на соответствующий гравитационный эталонный эквивалент по силе:
Gn = (Mn/Mрт.)^2 х Gрт.
Подставляя развёрнутые значения Fпр.св., Fпр.рт., Gсв., Gрт.
отыскиваем собственные ускорения гравитационных втягивающих сил для каждого шара в центре другого.
«Попутно» проявляются численные значения гравитационной постоянной:
G = Gсв./ (Mсв.)^2 = 2,40172х10^-3 кгм^3/c^2 / (6х10^3кг)^2 =6,67144х10^-11м^3/c^2кг
G = Gрт./(Мрт.)^2 = 1,6679х10^-9 кгм^3/c^2 / 25кг^2 = 6,6716х10^-11 м^3/c^2кг
Отметим, что исходным посылом для наших рассуждений была только сила притяжения между ртутным и свинцовым шарами, полученная из опыта. Всё. Никаких формул, относящихся к закону тяготения Ньютона не использовалось. Значение гравитационной постоянной не вводилось, да оно и не появлялось в ходе формулировок, а проявилось в качестве императива-детерминанта поля тяготения каждого шара при вычислении собственных ускорений шаров.
Исходя из полученных формул можно заключить,что при арифметическом росте массы, её гравитационная энергия увеличивается пропорционально квадрату массы:
Gn = G M^2
А из формулы ускорения: а = G M/r^2
предварительно считаем, что гравитационная постоянная это удельное ускорение втягивания собственной гравитационной силой собственной инертной массы, действительное для любой плотности вещества (в системе СИ).
Перейдём к появившейся формуле притяжения одного тела другим:
Fпр. = Fвт. х М1/М2
Каждое тело притягивает другое силой пропорциональной обратному отношению масс. Фактически это другая интерпретация закона тяготения. При этом возникают следствия, которые не проявляются, исходя из прямой пропорциональности взаимодействующих масс. В частности, при вычислении необходимой скорости для спутника Земли, в формуле присутствует и его масса.
Мы определили гравитационные силы, сопровождающие взаимодействие ртутного и свинцового шаров, с их помощью вычислили Гравитационную постоянную, но что означает, что гравитационная втягивающая сила ртутного шара в
6,7388х10^-6 н /5,6157х10^-9 н = 1200 раз меньше своей силы притяжения? Мы же исходили из равенства сил притяжения шаров, и стрелка весов показала её величину?
Эти силы притяжения действительно равны, НО! За чей «счёт»?
Можно было бы считать, что ВСЯ гравитационная втягивающая сила свинцового шара на расстоянии до центра ртутного расходуется на уравновешивание и дополнение силы ртутного шара? Ведь она в точности, в 1200 раз больше силы притяжения, и это она дополняла бы гравитационную силу ртутного шара до необходимой?
Но в таком случае, весы и показали бы силу притяжения 8,0866х10^-3 н, что в десяки раз больше определённой из опыта.
Однако, главное заключается в том, что гравитационная сила свинцового шара 8,0866х10^-3 распределяется пропорционально массам взаимодействующих тел, и кроме силы притяжения со своей стороны, для ртутного ничего гравитационного свинцовый шар добавить не может.
Во взаимодействии ртутного и свинцового шаров неявно участвуют инерциальные силы их инертных масс. Это высвобожденная инерциальная сила инертной массы свинцового шара величиной 6,7388х10^-6 н дополнила гравитационную втягивающую силу ртутного шара до, якобы его,силы притяжения и сдвинула стрелку весов на 0,7 мг. При этом, если бы и свинцовый шар стоял на весах, они бы показали, что он «похудел» за время опыта на 0,7 мг
Гравитационные силы шаров, будь они сами по себе, даже не качнули бы стрелку весов, хотя бы и вплотную посади ртутный шар на свинцовый.
1. Гравитационных эквивалент Земли:
Gз = (Мз / Мсв.)^2 х Gсв.= 2,3825х10^39 кгм^3/c^2
2. Гравитационная втягивающая сила на поверхности Земли:
3. Ускорение на поверхности Земли:
а = Fвт.з./ Мз = 9,8 м/с^2
4. Гравитационная втягивающая сила в точке на расстоянии до Луны:
5. Эта сила распределяется пропорционально массам Земли и Луны:
Fпр.л.= Fз.-л.х Мл./Мз = 1,978х10^20н
6. Ускорение с которым Земля втягивает Луну (напряжённость поля тяготения Земли в любой точке орбиты Луны):
1,978х10^20н / 7,33х10^22кг = 2,7х10^-3 м/с^2
7. Fз.-л. можно определить ещё и как произведение массы Земли на ускорение, с которым Земля втягивает Луну:
Fз.-л. = Мз х 2,7х10^-3 = 1,612х10^22 н
Теперь подставим в п.5 вместо Fз.-л. его произведение:
Fпр.л. = Мз х 2,7х10^-3 х Мл./Мз
но ускорение 2,7х10^-3 м/c^2 = G Мз / r^2 тогда получаем
Fпр.л. = Мз х G х Мз / r^2 х Мл./Мз сокращая Мз, получаем
полноценную формулу закона всемирного тяготения. Т.е в вычисленной силе Fз.-л. уже присутствовала, но неявно, гравитационная постоянная. И не замени мы силу Fз.-л. на равное ей произведение массы на ускорение, то не получили бы «перехода » формулы с обратной пропорциональностью масс в формулу с прямой пропорциональностью взаимодействующих масс, что свидетельствует о равенстве по модулю сил притяжения и инерционных сил взаимодействия (ц.стр. и цб. сил).
Мы исходили из обратной пропорциональности инертных масс, и для получения искомых величин вовсе не требовалась гравитационная постоянная. По массе пробного тела и его гравитационному эквиваленту, радиусу планеты и ускорению на её поверхности можно найти массу любой планеты, не используя гравитационную постоянную.
Однако, она «главное действующее лицо» и не только в законе всемирного тяготения, хотя Ньютон её в закон и не вводил.
Само понятие слова УДЕЛЬНЫЙ связано с единицей свойства тела или единицей объёма, веса и т.п., поэтому можно сказать:
Если в состоянии устойчивого равновесия двух тел существуют силы пропорциональные обратному отношению их инертных масс, то существуют противодействующие им силы, равные по модулю и пропорциональные произведению этих масс. Для каждого тела:
F2 х М1/М2 = G/r^2 M1 х M2
F1 х М2/М1 = G/r^2 M2 Х М1
Каждое небесное тело воздействует и отвечает на воздействие своими гравитационными силами и тем самым запускают работу внутренних сил той же природы каждого тела по вращению и перемещению этих тел. Но это уже, как говорят, другая история.
Физический смысл гравитационной постоянной
Гравитационная постоянная – это коэффициент в законе всемирного тяготения:
Закон «всемирного тяготения» был выведен Ньютоном, и описывал «силу притяжения» между двумя телами с массами m1 и m2.
Но каков же физический смысл гравитационной постоянной? Правильно ли мы понимаем суть закона всемирного тяготения?
Не кажется ли вам странным, что закон описывает взаимодействие ДВУХ тел, совершенно не учитывая влияние других? В то время как ВСЕМИРНОЕ тяготение – это явление, охватывающее взаимодействие всех тел во вселенной.
Значение гравитационной постоянной было неизвестно Ньютону. И он даже не знал, каким образом его можно было бы рассчитать. Это сделал другой ученый – Кавендиш – в 1798 году.
В этом небольшом видео очень хорошо демонстрируется сам эксперимент:
Внимательно просмотрев видео и проанализировав данный эксперимент, можно прийти к заключению, что массы шаров тут вообще ни при чем. Никакого «гравитационного притяжения» между ними нет.
Более того, скорее всего, эксперимент с крутильными весами на другой планете даст совсем другое значение «гравитационной постоянной», а значение 6,67 – это локальная константа, характерная именно для Земли, с её скоростью вращения и траекторией движения.
Обратите внимание, как поставлен эксперимент. В нём используются ВЕСЫ. Это очень важная деталь эксперимента. Без неё эксперимент не удастся. Если вы просто подвесите на нитках два шарика, то между ними не будет никакого притяжения. И никакие сверхточные измерения этого не зафиксируют.
А что такое весы? Это гармоническая, самоуравновешивающаяся система, которая балансирует за счет взаимодействия с Землей. И в данном эксперименте мы рассматриваем взаимодействие двух весов, которые стремятся уравновеситься с движением Земли! Однако экспериментатор приписывает эффект притяжения самим шарикам, полностью игнорируя влияние Земли и её движения! И это главная ошибка, которая приводит ко множеству других логических ошибок и неверных выводов.
Физический смысл закона «всемирного тяготения» заключается в том, что вся вселенная – это единая гармоническая система, стремящаяся к равновесию. Отсюда и вытекают все закономерности движений небесных тел и распределения материи во вселенной, то есть все временные и пространственные закономерности.
Но для понимания всей глубины этого универсального закона вселенной недостаточно вычисления константы, нужно уметь чувствовать, осознавать действие этих законов в самом себе. И тогда он становится не просто сухой формулой, а универсальным нравственным законом развития и бытия.
3. Физическая сущность гравитации
Анализируя современные теории гравитации, начиная с Ньютона и его последователей, мы видим сложность восприятия этого явления. Она заключается в том, что термин «тяготение» ассоциируется с термином «гравитационное излучение». Но если это излучение, т.е. нечто, исходящее от гравитирующего тела (например, Земли), то, как оно может действовать в обратном направлении, т.е. притягивать? Гегель указывал на это несоответствие ещё 200 лет назад. Он считал, что притяжение есть производное от отталкивания, однако, обосновать это теоретически не удосужился.
Физика не может использовать интуитивные прозрения, если их нельзя сформулировать последовательным математическим языком и дополнить описанием на обычном языке. Кроме того, существующие сегодня теории гравитации, включая закон всемирного тяготения Ньютона и общую теорию относительности Эйнштейна, не отвечают на самый главный вопрос – откуда берётся энергия на создание и поддержание гравитационного поля. По расчётам учёных сила притяжения Солнца, удерживающая Землю на орбите, составляет 3,6х10^(21)кгс. Но кроме Земли надо притягивать и другие планеты. Учёные попали в тупик, выяснив, что Солнце не в состоянии энергетически обеспечить притяжение планет солнечной системы. Ньютон, да и Эйнштейн долго бились над этим вопросом, но так и не нашли разумного ответа. В конце концов, Ньютон решил, что сама масса является источником силы притяжения. Так появилась гравитационная масса, которую он отделил от веса. Но при этом ему пришлось внести в свою теорию другую массу – инертную, как количество вещества. К его удивлению, математические вычисления показали, что эти массы в точности равны друг другу. Так родился закон эквивалентности тяжёлой и инертной массы, который Эйнштейн использовал для построения общей теории относительности. Таким образом, Ньютон отказался от физического объяснения наблюдаемых явлений, заменив его математическим. По его пути пошёл и Эйнштейн, создавая свою теорию гравитации, в которой доминирующую роль играет не масса, а пространство и время, как физические объекты. Поэтому его теорию называют ещё геометрической. Конечно, геометрия может определять параметры сил, но она не может быть причиной движения.
В ХХ веке появилась, и начала быстро развиваться квантовая теория микромира и отдельная её ветвь – квантовая теория гравитации. Её трудность, прежде всего, заключается в том, что она основана на математическом формализме довольно высокого уровня, когда по результатам вычислений судят о физической сущности рассматриваемого явления. Кроме того, она постулирует наличие в природе элементарных частиц – гравитонов, ответственных за гравитационное взаимодействие. Как известно, несмотря на долгие поиски, эти частицы так и не были обнаружены. К тому же, эта теория, как и все предыдущие, не отвечает на вопрос – где находится источник энергии, питающий гравитационное поле. Итак, все перечисленные выше теории, а также подобные им (сегодня их насчитывается более десятка) являются чисто математическими, с невыявленной физической сущностью. Такие теории не дают выхода на проведение экспериментов, подтверждающих их. Объясняя отсутствие широкомасштабных экспериментов с гравитацией, учёные ссылаются на то, что, согласно теории Ньютона, для их проведения требуется огромная масса, поскольку именно она является источником гравитационных сил, а это практически невыполнимо. Что же касается общей теории относительности Эйнштейна, то в ней, как уже отмечалось, одна математика, а физической сущностью выступают пространство и время, которые не поддаются экспериментам. Не в лучшем виде в этом вопросе выглядит и квантовая теория гравитации. А, как уже говорилось в главе 1, при использовании математических методов в решении задач, необходимо соблюдать осторожность.
В первую очередь, для проверки термодинамической природы гравитации необходимо создать искусственное гравитирующее тело. До сих пор такая идея не могла прийти в голову ни одному исследователю, поскольку она противоречила бы всем известным на сегодня теориям гравитации. Однако, согласно ТМГ, процессы, связанные с излучением гравитационных волн Землёй можно сымитировать в миниатюре. Сама природа подсказывает, как это можно осуществить, причём очень просто и наглядно. Для этого необходимо взять шар, желательно побольше, из материала, выдерживающего высокую температуру. Внутрь его поместить источник тепловой энергии и установить этот шар на весы. Предположительно, он должен терять в весе (конечно незначительно) вследствие того, что своим гравитационным излучением будет отталкиваться от подобного излучения Земли (так же как Луна). Так и произошло. Для решающего эксперимента был изготовлен стальной шар диаметром 100мм. В шаре было сделано конусное отверстие до центра. Затем его поставили на лабораторные весы рычажного типа ВЛТ-5 с ценой деления 0,3г и уравновесили обычными гирями. Вес шара составил 4,2кг. В качестве источника тепловой энергии был использован лазер ЛТ1-2 с энергией луча 5 кВт. Луч был направлен в конусное отверстие шара сверху вниз. По мере повышения температуры поверхности шара (измерение проводилось термопарой) стрелка весов, как и предполагалось, медленно отклонялась в сторону уменьшения веса. Приблизительно через полтора часа, при достижении температуры поверхности шара 300°С лазер был выключен. Разница (уменьшение) в весе шара по сравнению с первоначальным показанием (в холодном состоянии) составила 3г (десять делений шкалы). При отключении лазера, вес вернулся к исходному.
Далее, чтобы разнообразить эксперименты, гравитирующее тело было изготовлено в форме тора, или, попросту говоря, большого бублика из каолинового волокна с «запеченной» внутри по оси электроспиралью мощностью 500Вт. Тепловой поток в нём, как и в шаре, распространяется изнутри по радиусу, т.е. будет направленным. Взвешивание «бублика» производилось на тех же весах, что и в предыдущем опыте. В этом эксперименте, как и в опыте с шаром, тепловая энергия на создание гравитационного излучения расходовалась со всей поверхности тора. При этом рабочая часть поверхности, которая взаимодействует с гравитационным излучением Земли, составляет 20-25% от всей его поверхности. Если бы вся энергия спирали была направлена в рабочую, нижнюю, зону тора, то эффект потери веса тора увеличился бы раз в 10. Это предположение можно отнести и к эксперименту с шаром. Выводы, полученные из этих двух опытов, послужили толчком для создания гравитирующего тела в виде «тарелки». Эта «летающая тарелка» была изготовлена из двух алюминиевых полусфер диаметром 350мм. В нижней полусфере установили графитовый сердечник (излучатель) диаметром и высотой 100мм. Нижний его торец выпустили на 10мм наружу, а на верхнем уложили электроспираль в фарфоровых бусах мощностью 0,8кВт. Всё остальное пространство обеих полусфер было заполнено каолиновым волокном. Вес «тарелки» в холодном состоянии составил 3,5кг, а гравитирующая способность (уменьшение веса) к концу эксперимента составила 5г. Взвешивание проводилось всё на тех же весах. Надо сказать, что здесь я ожидал лучшего результата. Очевидно, большая часть теплового потока, проходящего через сердечник, отклонялась в стороны для прогрева теплоизоляции его боковой поверхности. В результате, только часть теплового потока преобразовалась в гравитационное излучение, которое взаимодействовало с подобным излучением Земли.
Наилучшие результаты, т.е. потеря веса, были получены на модели гравитирующего тела, в шутку названного «летающая кастрюля», по аналогии с «летающей тарелкой». Эта модель и в самом деле была изготовлена из кастрюли с диаметром и высотой 160мм. В днище вырезали отверстие диаметром 100мм, на которое уложили диск из графита диаметром 130мм и толщиной 35мм. На диск, как и в предыдущем эксперименте, уложили электроспираль в фарфоровых бусах мощностью 600Вт. Всё свободное пространство «кастрюли» заполнили каолиновым волокном. Вес модели в холодном состоянии составил 2,534кг. На этот раз взвешивание проводилось на электронных весах МК-6-А20 с ценой деления 2г. Это позволило наблюдать за изменением веса модели во времени вплоть до минут в процессе её нагревания, а затем остывания в естественных условиях. Модель была установлена на специальной подставке, исключающей возможность нагрева механизма весов. Результаты эксперимента сведены в таблицу.(см. таблицу изменения веса модели при нагреве и остывании)