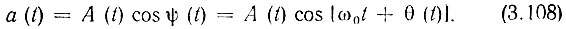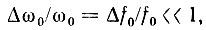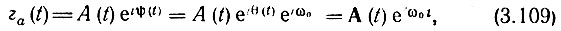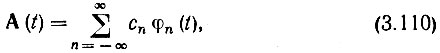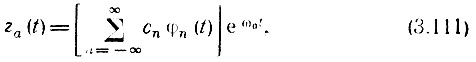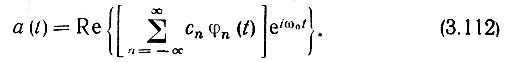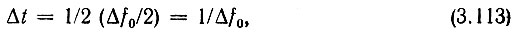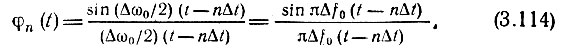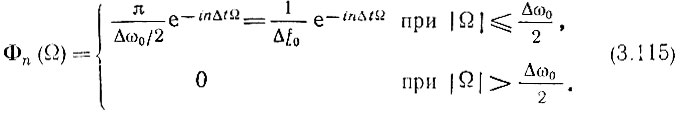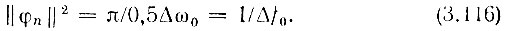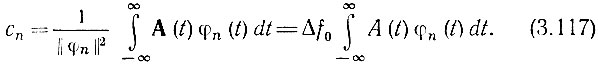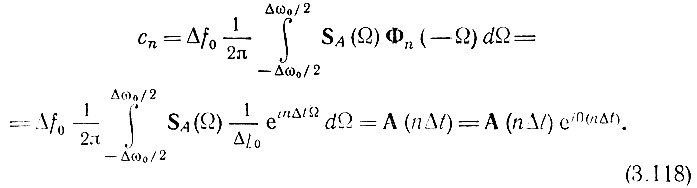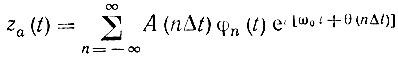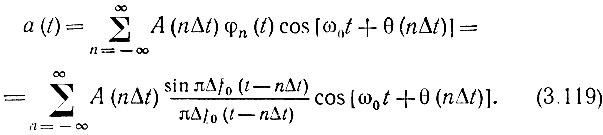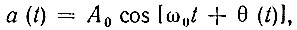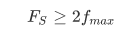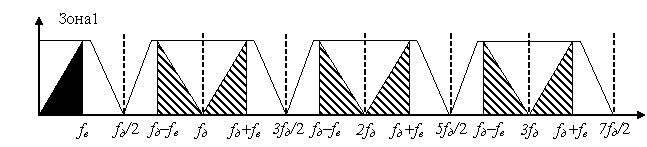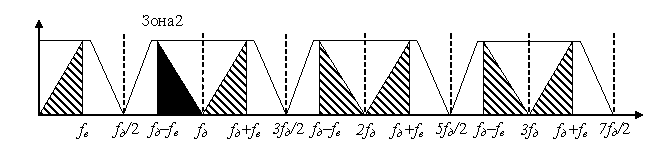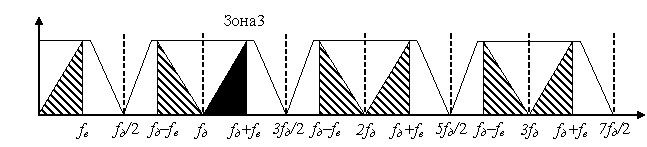в чем заключается эффект гетеродина при дискретизации относительно узкополосного сигнала
В чем заключается эффект гетеродина при дискретизации относительно узкополосного сигнала
3.12. Дискретизация узкополосного сигнала
Пусть задан сигнал
спектр которого заключен в узкой полосе частот от ω1 до ω2, так что модуль спектральной плотности Sa(ω) имеет вид, представленный на рис. 3.30, а, причем в пределах полосы Δω0 спектр не обязательно симметричен относительно центральной частоты ω0 = (ω1 + (ω2)/2. Под узкополосностью сигнала подразумевается условие
где 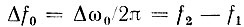
Предполагается, что функция A(t) является простейшей огибающей, т. е. что A(t) и ψ(t) отвечают соотношениям (3.60) и (3.61).
Для этого перейдем к аналитическому сигналу, соответствующему заданной функции a(t):
где комплексная огибающая A(t) = А(t) е iθ(t) представляет собой низкочастотную функцию, спектр которой SA(Ω) примыкает к нулевой частоте (рис. 3.30, б). Разложим комплексную функцию A(t) = А (t) е iθ(t) по ортогональной системе
где базисная функция φn(t) определяется выражением (2.121).
Подставив этот ряд в (3.109), получим
после чего исходное колебание a(t) определим как действительную часть функции za(t):
Как видим, задача дискретизации высокочастотного колебания свелась к задаче дискретизации комплексной огибающей А(t). При определении наибольшего допустимого интервала между выборками в разложении (3.110) необходимо исходить из наивысшей частоты в спектре функции А(t), Из определения ω0 как средней частоты в полосе Δω0 очевидно, что эта частота, отсчитываемая от Ω = 0, равна Δω0/2, или в герцах Δf0/2. Следовательно, интервал между выборками не должен превышать
а функция φn(t) должна иметь вид
От аналогичной функции, использованной в § 2.14, φn(t) отличается только заменой ωm на Δω0/2. Следовательно, спектральная плотность Ф0(Ω) функции 966;0(t) равна 2π/Δω0 = 1/Δf0 в полосе частот 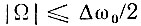
Квадрат нормы функции φn(t) по аналогии с выражением (2.123)
Далее по формуле (2.9) с учетом (3.116)
* ( Поскольку здесь рассматривается спектр огибающей.)
Итак, коэффициенты ряда (3.110) являются выборками функции А(t), взятыми через интервалы Δt = 1/Δf0.
Подставляя (3.118) в (3.111), получаем
и по формуле (3.112) определяем
При заданной длительности сигнала Тс число отсчетных точек 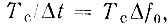
Следует иметь в виду, что при несимметричном (в полосе Δω0) спектре введенная в данном параграфе частота ω0 = (ω1 + ω2)/2 может не совпадать со «средней частотой» в выражении (3.73). Иными словами, фаза θ(t) может содержать слагаемое, линейно зависящее от времени.
Проиллюстрируем выражение (3.119) на примерах колебания, промодулированного по амплитуде или по частоте.
Иными словами, при чисто амплитудной модуляции число степеней свободы модулированного колебания такое же, как и число степеней свободы модулирующей функции.
Рассмотрим теперь частотно-модулированное колебание
когда мгновенная частота ω(t) = ω0 + dθ/dt модулирована тем же сообщением, что и в предыдущем случае, причем максимальная девиация частоты fд велика по сравнению с Fm, так что ширину Δfчм полосы частот модулированного колебания можно приравнять к 2fд [случай «широкополосной» частотной модуляции, (3.34)]. Интервал между выборками должен быть взят Δt ≤ 1/Δfчм = 1/2fд. Так как при ЧМ амплитуда колебания неизменна, то передавать ее нет необходимости. Следовательно, для однозначного представления частотно-модулированного колебания достаточно задавать фазу θ (nΔt) этого колебания в отсчетных точках, отстоящих одна от другой на время Δt ≤ 1/2fд. При одной и той же длительности сообщения Тс число выборок фазы при ЧМ равно ΔfчмTс = 2fдТс, а число выборок огибающей при АМ равно ΔfамTc = 2FmTc. Отсюда видно, что при одинаковом передаваемом сообщении (при одинаковом количестве информации) частотно-модулированный сигнал обладает числом степеней свободы в fд/Fm = m раз большим, чем амплитудно-модулированный сигнал. Это является результатом расширения спектра сигнала при ЧМ. На приемной стороне канала связи после частотного детектирования модулированного колебания выделяется напряжение, которое имеет спектр и число степеней свободы такие же, как и исходное сообщение.
Из приведенного примера видно, что при одной и той же ширине спектра информационная емкость радиосигнала различна в зависимости от вида модуляции.
Дискретизация сигнала на промежуточной частоте (субдискретизация)
До сих пор мы рассматривали случай дискретизации низкочастотных сигналов (звуковых, видеосигналов или огибающих дискретного сигнала), когда все интересующие нас сигналы находятся в первой зоне частот Котельникова. На рисунке 1. представлен именно этот случай, когда полоса частот полезного сигнала ограничена первой зоной Котельникова, а на выходе дискретизатора в остальных зонах Котельникова появляются образы полезного сигнала. На этом рисунке полоса частот полезного сигнала выделена черным цветом.
Рисунок 1. Дискретизация низкочастотного сигнала.
Теперь рассмотрим случай, показанный на рисунке 2, где полоса полезного сигнала полностью находится во второй зоне Котельникова. Часто процесс дискретизации сигнала, находящегося вне первой зоны Котельникова, называется субдискретизацией или дискретизацией полосового сигнала.
Рисунок 2. Субдискретизация сигнала, находящегося во второй зоне Котельникова.
Такая ситуация часто возникает при обработке сигнала на выходе радиоприемника. В радиоприемниках сигнал обычно переносится на промежуточную частоту. При этом гарантируется, что сигнал за пределами полосы пропускания фильтра промежуточной частоты отсутствует. Это требуется для работы и аналогового приемника.
Отметим, что образ сигнала в первой зоне Найквиста, образующийся на выходе дискретизатора, содержит всю информацию об исходном сигнале, за исключением его первоначального местоположения на оси частот. Для четных зон Котельникова, порядок частот в спектре образа сигнала в первой зоне Котельникова обратный, и это следует учитывать при дальнейшей обработке оцифрованного сигнала.
Рисунок 3. Субдискретизация сигнала, находящегося в третьей зоне Котельникова.
На рисунке 3. показан вариант дискретизации сигнала, расположенного в третьей зоне Найквиста. Отметим, что в этом случае в сигнале, образующемся на выходе дискретизатора в первой зоне Котельникова, обращения частот не происходит.
Итак, частоты подлежащих дискретизации сигналов могут лежать в любой зоне Котельникова, и сигнал в первой зоне Котельникова является точным образом исходного сигнала (за исключением обращения частот, которое происходит, когда сигналы расположены в четных зонах Котельникова).
Сейчас мы можем уточнить сформулированный ранее критерий преобразования сигнала в цифровую форму по Котельникову:
Сигнал должен быть дискретизирован со скоростью равной или большей удвоенной полосы частот полезного сигнала для того, чтобы сохранить всю информацию об исходном сигнале.
Обратите внимание, что в этой формулировке нет никакого упоминания об абсолютном местоположении дискретизируемого сигнала в частотном спектре относительно частоты дискретизации. Единственное ограничение заключается в том, что полоса подлежащих дискретизации сигналов должна быть ограничена одной зоной Найквиста. Частотные компоненты дискретизируемых сигналов не должны пересекать частоту fд/2 с любым коэффициентом (это и является основной задачей аналогового фильтра, размещаемого на входе аналого-цифрового преобразователя).
Дискретизация сигналов, лежащих выше первой зоны Найквиста, стала популярной в аппаратуре связи, так как этот процесс эквивалентен аналоговой демодуляции. Обычным становится дискретизация сигналов ПЧ с последующим использованием цифровых методов для обработки сигнала. Таким способом исчезает необходимость использования демодулятора ПЧ. Ясно, что с ростом ПЧ растут и требования к производительности АЦП. Ширина полосы частот на входа АЦП и характеристики, связанные с допустимыми искажениями сигналов, должны быть адекватны скорее ПЧ, чем основной полосе частот. Это является проблемой для большинства АЦП, предназначенных для обработки сигналов в первой зоне Найквиста, поэтому для субдискретизации требуется АЦП, который может обрабатывать сигналы в более высокочастотных зонах Котельникова.
Понравился материал? Поделись с друзьями!
Вместе со статьей «Дискретизация сигнала на промежуточной частоте (субдискретизация)» читают:
Субдискретизация сигнала промежуточной частоты
Данная статья полностью теоретическая и является прологом для последующих, в которых я постараюсь сделать небольшое исследование в области субдискретизации узкополосных высокочастотных сигналов и их цифровой обработки. Я не эксперт в области цифровой обработки сигналов, а только учусь), так что пока постараюсь обойтись без сложных формул, они будут в следующей статье.
Сразу дадим определение:
процесс дискретизации сигнала, находящегося вне первой зоны Котельникова-Найквиста.
Чтобы понять, что такое субдискретизация, нужно для начала понять, что такое собственно дискретизация, что такое зоны Котельникова-Найквиста, что происходит в процессе дискретизации и где это может использоваться. Начнем понемногу.
О дискретизации
это определение значений непрерывного сигнала (например, аналогового) в дискретные моменты времени.
По теореме о дискретном представлении, чтобы выборки полностью описывали сигнал, дискретизация должна осуществляться на частоте:
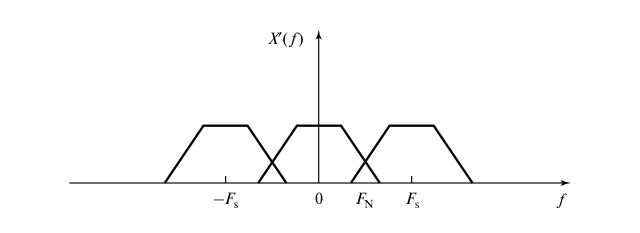
На рисунке ниже показан процесс дискретизации, который можно рассматривать как умножение аналогового сигнала x(t) на выборочную функцию p(t). Функция p(t) состоит из импульсов единичной амплитуды бесконечно малой длительности и периодом T. На рисунке также показаны спектры сигналов. X'(f) — это свертка X(f) и P(f), следовательно умножение во временных координатах экививалентно свертке в частотных координатах.
Можно увидеть как отличаются спектры сигнала до (б) и после (г) дискретизации и можно заметить, что спектр дискретного сигнала повторяется в точках, кратных частоте дискретизации Fs.
Про дискретный сигнал можно отметить следующие моменты:
На практике наложение присутствует всегда, из-за шума и наличия сигналов за пределами полосы частот полезного сигнала, следовательно главная задача разработчика создать подходящий фильтр для защиты от наложения спектров, обеспечивающий достаточное подавление (с учетом разрешающей способности АЦП) на частотах, превышающих частоту Котельникова-Найквиста, а также выбрать подходящую частоту дискретизации.
Более подробно описывать фильтрацию от наложения спектра я не буду, т.к. это выходит за пределы темы статьи. Кому интересно, найдет данную информацию в книгах или может почитать тут про антиалайзинговый фильтр. Также опущу факторы, которые влияют на выбор частоты дискретизации, это тема для отдельной статьи, которая будет позже.
О субдискретизации
Часто бывает, что, например, в системах связи, полезный сигнал занимает только узкую часть доступной полосы частот. Это относится к дискретизации сигнала на промежуточной частоте в приемниках. Выше мы рассматривали случаи дискретизации низкочастотных сигналов, которые полностью находятся в первой зоне Котельникова-Найквиста. На следующем рисунке показан случай, когда полоса частот полезного сигнала ограничена первой зоной дискретизации, а на выходе дискретизатора в остальных зонах появляются образы полезного сигнала, как уже об этом говорилось выше.
Теперь взглянем на случай, когда полоса сигнала находится во второй зоне Котельникова-Найквиста.
Именно такая ситуация возникает при обработке сигнала радиоприемника, где сигнал переносится на промежуточную частоту и гарантируется, что сигнал за пределами полосы пропускания фильтра промежуточной частоты отсутствует. Дадим еще раз определение субдискретизации:
процесс дискретизации сигнала, находящегося вне первой зоны Котельникова-Найквиста.
Образ сигнала в первой зоне Котельникова-Найквиста содержит всю информацию об исходном сигнале, кроме его первоначального положения на оси частот. Для четных зон Котельникова-Найквиста, порядок частот в спектре образа сигнала в первой зоне обратный и это следует учитывать при обработке.
Рассмотрим образ сигнала в третьей зоне Котельникова-Найквиста, здесь уже на выходе дискретизатора в первой зоне, обращения частот не происходит. Таким образом, полоса частот сигнала, подлежащая дискретизации может лежать в любой зоне Котельникова-Найквиста и сигнала в первой зоне является точным образом исходного сигнала, за исключением обращения частот, которое проиходит в четных зонах Котельникова-Найквиста. Дадим еще одну формулировку:
Сигнал должен быть дискретизирован со скоростью равной или большей удвоенной полосы частот полезного сигнала для того, чтобы сохранить всю информацию об исходном сигнале.
В данной формулировке нет никакого упоминания о положении сигнала в частотном спектре относительно частоты дискретизации, главное, чтобы он был ограничен одной зоной Котельникова-Найквиста и его частотные компоненты не должны выходить за частоту Fs/2, что является задачей для антиалайзингового фильтра, который размещается до аналого-цифрового преобразователя.
Данная техника дискретизации используется в приемной аппаратуре, как я уже писал выше. Процесс эквивалентен аналоговой демодуляции с последующей цифровой обработкой сигнала. Это позволяет избавиться от демодулятора промежуточной частоты, однако накладывает определенные требования на производительность АЦП, который должен работать в более высокочастотных зонах Котельникова-Найквиста и вносить минимальные искажения во входной сигнал, именно такие АЦП используются для субдискретизации.
В следующей статье из данной серии рассмотрим некоторые практические примеры выбора частоты дискретизации, что-нибудь посчитаем, попробуем задействовать для этих целей GNU Octave, о котором я уже писал ранее. А пока подписывайтесь на обновления блога в Твиттер и ВК, а также заходите в наш чат Телеграм.
Алиасинг при дискретизации сигналов
DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
Распространяется под лицензией LGPL v3
В предыдущих параграфах мы неоднократно говорили, что при дискретизации аналогового сигнала происходит бесконечное периодическое копирование спектральной плотности сигнала c периодом, равным частоте дискретизации рад/с.
В данном разделе мы проанализируем данный эффект и рассмотрим пути подавления алиасинга при дискретизации сигналов.
Ввиду того, что спектральная плотность после дискретизации становится периодической, с периодом равным рад/с, мы можем разбить ось частот на зоны шириной как это показано на рисунке 1
Частотные зоны, показанные на рисунке 1, носят название зон Найквиста. При этом выделяют первую зону Найквиста, занимающую полосу рад/с, а также высшие зоны: вторую, третью и т.д.
Можно видеть, что при дискретизации сигнала, спектральные компоненты «размножаются» во все зоны Найквиста, в результате сигнал из высшей зоны (заштрихованные компоненты) отображается в первую зону. Такое «просачивание» сигнала из высшей зоны Найквиста в первую зону называется эффектом наложения [2, стр. 168], или алиасингом [1] [1, стр. 197].
Важно отметить, что по дискретному сигналу невозможно определить из какой зоны Найквиста исходный аналоговый сигнал был дискретизирован.
Если исходный аналоговый сигнал будет представлен сразу в нескольких зонах Найквиста, то при дискретизации произойдет смешение спектральных компонент сигнала, как это показано на рисунке 3
Спектральная плотность входного аналогового сигнала представлена в первой и третьей зонах одновременно (рисунок 3а). Тогда на выходе АЦП мы будем иметь дискретный сигнал, чья спектральная плотность показана на рисунке 3б. Копии спектральной плотности из третье зоны Найквиста смешиваются с сигналом в первой зоне, и мы не сможем их разделить в цифровой области.
Разумеется, последний пример не выполняет условий теоремы Котельникова, в результате чего алиасинг вносит неустранимые искажения в дискретный сигнал на выходе АЦП. В большинстве случаев алиасинг вреден и требуется применять методы для его устранения при дискретизации сигналов.
Подавить алиасинг на выходе АЦП можно при помощи аналогового ФНЧ с частотй среза равной частоте Найквиста (половине частоты дискретизации), как это показано на рисунке 4.
На верхнем графике показана спектральная плотность исходного сигнала (как на рисунке 3), содержащая компоненты в первой и третьей зонах Найквиста. Также показана АЧХ аналогового ФНЧ, который пропускает только сигнал в первой зоне Наквиста и подавляет сигнал во всех высших зонах. В результате вход АЦП не будет содержать компонент из высших зон Найквиста и на выходе АЦП алиасинг не будет наблюдаться.
Таким образом, ФНЧ перед АЦП призван гарантировать соблюдение условий теоремы Котельникова при дискретизации сигнала.
Разумеется, реальные ФНЧ не могут обеспечить полного подавления в полосе заграждения, но могут обеспечить подавление до заданного уровня, например до уровня шумов АЦП. При этом будут наблюдаться незначительные искажения сигнала в полосе пропускания ФНЧ в первой зоне Найквиста. Допустимый уровень искажений в полосе пропускания должны быть заданы при проектировании ФНЧ.
В предыдущих параграфах мы рассмотрели эффект алиасинга в частотной области, возникающий в результате копирования спектральной плотности при дискретизации сигнала. В данном параграфе мы покажем эффект алиасинга во временно́й области.
Пусть исходный сигнал имеет вид (см. рисунок 5а):
Возьмем дискретные отсчеты сигнала (2) с периодом с. Тогда частота дискретизации Гц, или рад/с. Частота Найквиста равна половине частоты дискретизации, т.е. рад/с.
Поскольку сигнал находится во второй зоне Найквиста, то при дискретизации мы будем иметь алиасинг, как это показано на рисунке 5в, и спектральная плотность будет иметь вид, показанный на рисунке 5г. Из рисунка 5г видно, что в первой зоне Найвиста появились компоненты на частотах рад/с. Во временно́й области это огибающая на частоте рад/с, причем по дискретному сигналу непонятно в какой зоне Найквиста находится исходный сигнал.
В конце данного раздела рассмотрим любопытный эффект, возникающий при дискретизации гармонического сигнала, расположенного на границе зон Найквиста (если частота дискретизации точно равна удвоенной частоте сигнала ).
Можно видеть, что дискретизация сигнала произведена в точках максимума и минимума и аналоговый сигнал может быть полностью восстановлен. Сигнал дискретизирован в нулях, в результате, все отсчеты данного сигнала равны нулю и сигнал полностью потерян.
Чтобы понять данный эффект необходимо вновь обратиться к (1), а также вспомнить выражения для спектральных плотностей и сигналов и соответственно
Для сигнала копии также попадают на одни и те же частоты, но при сложении взаимно уничтожаются, потому что имеют различные знаки. В результате спектральная плотность дискретного сигнала становится тождественно равна нулю, что мы и видим во временной области.
Приведенный пример демонстрирует эффект который возникает при попадании сигнала на границу зон Найквиста. Часто при формулировке теоремы Котельникова говорят [3, 4], что частота дискретизации должна быть больше или равна удвоенной верхней частоте сигнала. Такая формулировка неточна, так как не учитывает приведенный граничный эффект. Поэтому правильнее говорить, что частота дискретизации должна быть строго больше верхней частоты сигнала для исключения граничных эффектов. И тут, необходимо отметить, что термин верхняя частота также видится не вполне корректным. И вот почему.
В таком подходе термин верхняя частота перестает играть роль. Важна полоса сигнала, потому что она определяет количество информации в сигнале. Если вернуться к теореме Котельникова, то она была изначально сформулирована в терминах полосы видеосигнала, причем мы требовали чтобы для исключения эффекта дискретизации на границах зоны Найквиста.
Если продолжать рассуждения, то можно пойти еще дальше, и не использовать полосу, а ставить частоту дискретизации напрямую в зависимость от количества информации в сигнале. Именно такой подход лег в основу техники дискретизации, которая носит название compressed sensing [6, 7] и является неким гибридным методом одновременной дискретизации и сжатия данных с возможностью полного восстановления и сокращения частоты отсчетов.
В данном разделе мы рассмотрели эффект алиасинга, возникающий при дискретизации аналоговых сигналов, если не соблюдать условия теоремы Котельникова.
Мы ввели понятие зон Найквиста и показали, что при дискретизации сигналов, представленных в нескольких зонах Найквиста наблюдается смешение частотных компонент на выходе дискретизатора.
Также мы рассмотрели использование аналогового фильтра для ограничении полосы сигнала при дискретизации для устранения эффекта алиасинга.
Алисаинг был продемонстрирован как во временной, так и в частотной областях.
В конце раздела мы продемонстрировали и пояснили краевой эффект при дискретизации гармонических сигналов на границе зон Найквиста.