в чем суть метода наименьших квадратов мнк
В чем суть метода наименьших квадратов?
Сущность метода наименьших квадратов заключается в отыскании параметров модели тренда, которая лучше всего описывает тенденцию развития какого-либо случайного явления во времени или в пространстве (тренд – это линия, которая и характеризует тенденцию этого развития).
Задача метода наименьших квадратов (МНК) сводится к нахождению не просто какой-то модели тренда, а к нахождению лучшей или оптимальной модели.
Метод наименьших квадратов
Эта модель будет оптимальной, если сумма квадратических отклонений между наблюдаемыми фактическими величинами и соответствующими им расчетными величинами тренда будет минимальной (наименьшей):
МНК самостоятельно применяется довольно редко. Как правило, чаще всего его используют лишь в качестве необходимого технического приема при корреляционных исследованиях.Следует помнить, что информационной основой МНК может быть только достоверный статистический ряд, причем число наблюдений не должно быть меньше 4-х, иначе, сглаживающие процедуры МНК могут потерять здравый смысл.
Инструментарий МНК сводится к следующим процедурам:
Первая процедура. Выясняется, существует ли вообще какая-либо тенденция изменения результативного признака при изменении выбранного фактора-аргумента, или другими словами, есть ли связь между «у» и «х».
Вторая процедура. Определяется, какая линия (траектория) способна лучше всего описать или охарактеризовать эту тенденцию.
Третья процедура. Рассчитываются параметры регрессионного уравнения, характеризующего данную линию, или другими словами, определяется аналитическая формула, описывающая лучшую модель тренда.
Пример. Допустим, мы имеем информацию о средней урожайности подсолнечника по исследуемому хозяйству (табл. 9.1).
| Номер наблюдения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Годы | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
| Урожайность, ц/га | 14,2 | 15,6 | 17,5 | 14,5 | 15,3 | 17,0 | 16,6 | 17,5 | 15,0 | 17,7 |
Поскольку уровень технологии при производстве подсолнечника в нашей стране за последние 10 лет практически не изменился, значит, по всей видимости, колебания урожайности в анализируемый период очень сильно зависели от колебания погодно-климатических условий. Действительно ли это так?
Первая процедура МНК. Проверяется гипотеза о существовании тенденции изменения урожайности подсолнечника в зависимости от изменения погодно-климатических условий за анализируемые 10 лет.
В данном примере за «y» целесообразно принять урожайность подсолнечника, а за «x» – номер наблюдаемого года в анализируемом периоде.
Проверку гипотезы о существовании какой-либо взаимосвязи между «x» и «y» можно выполнить двумя способами: вручную и при помощи компьютерных программ. Конечно, при наличии компьютерной техники данная проблема решается сама собой.
Но, чтобы лучше понять инструментарий МНК целесообразно выполнить проверку гипотезы о существовании связи между «x» и «y» вручную, когда под рукой находятся только ручка и обыкновенный калькулятор.
В таких случаях гипотезу о существовании тенденции лучше всего проверить визуальным способом по расположению графического изображения анализируемого ряда динамики — корреляционного поля:

Корреляционное поле в нашем примере расположено вокруг медленно возрастающей линии. Это уже само по себе говорит о существовании определенной тенденции в изменении урожайности подсолнечника.
Нельзя говорить о наличии какой-либо тенденции лишь тогда, когда корреляционное поле похоже на круг, окружность, строго вертикальное или строго горизонтальное облако, или же состоит из хаотично разбросанных точек.
Во всех остальных случаях следует подтвердить гипотезу о существовании взаимосвязи между «x» и «y», и продолжить исследования.
Вторая процедура МНК. Определяется, какая линия (траектория) способна лучше всего описать или охарактеризовать тенденцию изменения урожайности подсолнечника за анализируемый период.
При наличии компьютерной техники подбор оптимального тренда происходит автоматически. При «ручной» обработке выбор оптимальной функции осуществляется, как правило, визуальным способом – по расположению корреляционного поля. То есть, по виду графика подбирается уравнение линии, которая лучше всего подходит к эмпирическому тренду (к фактической траектории).
Как известно, в природе существует огромное разнообразие функциональных зависимостей, поэтому визуальным способом проанализировать даже незначительную их часть — крайне затруднительно.
К счастью, в реальной экономической практике большинство взаимосвязей достаточно точно могут быть описаны или параболой, или гиперболой, или же прямой линией.
В связи с этим, при «ручном» варианте подбора лучшей функции, можно ограничиться только этими тремя моделями.
| Прямая: | Гипербола: |
 |  |

Нетрудно заметить, что в нашем примере лучше всего тенденцию изменения урожайности подсолнечника за анализируемые 10 лет характеризует прямая линия, поэтому уравнением регрессии будет уравнение прямой.
Третья процедура. Рассчитываются параметры регрессионного уравнения, характеризующего данную линию, или другими словами, определяется аналитическая формула, описывающая лучшую модель тренда.

В линейном уравнении параметр – коэффициент регрессии указывает, на сколько единиц в среднем изменится с изменением на единицу. Он имеет единицу измерения результативного признака.
В случае прямой связи – величина положительная, а при обратном – отрицательная. Параметр – свободный член уравнения регрессии, то есть это значение при. Если не получает нулевых значений, этот параметр имеет лишь расчетное назначение.
Приведем также системы нормальных уравнений для отыскивания параметров нелинейных уравнений.
| Форма связи | Уравнение связи | Система нормальных уравнений |
| параболическая |  | |
| гиперболическая |
Следует помнить, что при изменении хотя бы одного значения входных данных (пары значенийили одного из них) все коэффициенты изменят в общем случае свои значения, потому что они полностью определяются входными данными. Поэтому при повторной аппроксимации с несколькими измененными данными будет получена другая аппроксимирующая функция с другими коэффициентами.
Математика на пальцах: методы наименьших квадратов
Я математик-программист. Самый большой скачок в своей карьере я совершил, когда научился говорить:«Я ничего не понимаю!» Сейчас мне не стыдно сказать светилу науки, что мне читает лекцию, что я не понимаю, о чём оно, светило, мне говорит. И это очень сложно. Да, признаться в своём неведении сложно и стыдно. Кому понравится признаваться в том, что он не знает азов чего-то-там. В силу своей профессии я должен присутствовать на большом количестве презентаций и лекций, где, признаюсь, в подавляющем большинстве случаев мне хочется спать, потому что я ничего не понимаю. А не понимаю я потому, что огромная проблема текущей ситуации в науке кроется в математике. Она предполагает, что все слушатели знакомы с абсолютно всеми областями математики (что абсурдно). Признаться в том, что вы не знаете, что такое производная (о том, что это — чуть позже) — стыдно.
Но я научился говорить, что я не знаю, что такое умножение. Да, я не знаю, что такое подалгебра над алгеброй Ли. Да, я не знаю, зачем нужны в жизни квадратные уравнения. К слову, если вы уверены, что вы знаете, то нам есть над чем поговорить! Математика — это серия фокусов. Математики стараются запутать и запугать публику; там, где нет замешательства, нет репутации, нет авторитета. Да, это престижно говорить как можно более абстрактным языком, что есть по себе полная чушь.
Знаете ли вы, что такое производная? Вероятнее всего вы мне скажете про предел разностного отношения. На первом курсе матмеха СПбГУ Виктор Петрович Хавин мне определил производную как коэффициент первого члена ряда Тейлора функции в точке (это была отдельная гимнастика, чтобы определить ряд Тейлора без производных). Я долго смеялся над таким определением, покуда в итоге не понял, о чём оно. Производная не что иное, как просто мера того, насколько функция, которую мы дифференцируем, похожа на функцию y=x, y=x^2, y=x^3.
Я сейчас имею честь читать лекции студентам, которые боятся математики. Если вы боитесь математики — нам с вами по пути. Как только вы пытаетесь прочитать какой-то текст, и вам кажется, что он чрезмерно сложен, то знайте, что он хреново написан. Я утверждаю, что нет ни одной области математики, о которой нельзя говорить «на пальцах», не теряя при этом точности.
Задача на ближайшее время: я поручил своим студентам понять, что такое линейно-квадратичный регулятор. Не постесняйтесь, потратьте три минуты своей жизни, сходите по ссылке. Если вы ничего не поняли, то нам с вами по пути. Я (профессиональный математик-программист) тоже ничего не понял. И я уверяю, в этом можно разобраться «на пальцах». На данный момент я не знаю, что это такое, но я уверяю, что мы сумеем разобраться.
Итак, первая лекция, которую я собираюсь прочитать своим студентам после того, как они в ужасе прибегут ко мне со словами, что линейно-квадратичный регулятор — это страшная бяка, которую никогда в жизни не осилить, это методы наименьших квадратов. Умеете ли вы решать линейные уравнения? Если вы читаете этот текст, то скорее всего нет.
Итак, даны две точки (x0, y0), (x1, y1), например, (1,1) и (3,2), задача найти уравнение прямой, проходящей через эти две точки:
Эта прямая должна иметь уравнение типа следующего:
Здесь альфа и бета нам неизвестны, но известны две точки этой прямой:
Можно записать это уравнение в матричном виде:
Тут следует сделать лирическое отступление: что такое матрица? Матрица это не что иное, как двумерный массив. Это способ хранения данных, более никаких значений ему придавать не стоит. Это зависит от нас, как именно интерпретировать некую матрицу. Периодически я буду её интерпретировать как линейное отображение, периодически как квадратичную форму, а ещё иногда просто как набор векторов. Это всё будет уточнено в контексте.
Давайте заменим конкретные матрицы на их символьное представление:
Тогда (alpha, beta) может быть легко найдено:
Более конкретно для наших предыдущих данных:
Что ведёт к следующему уравнению прямой, проходящей через точки (1,1) и (3,2):
Окей, тут всё понятно. А давайте найдём уравнение прямой, проходящей через три точки: (x0,y0), (x1,y1) и (x2,y2):
Ой-ой-ой, а ведь у нас три уравнения на две неизвестных! Стандартный математик скажет, что решения не существует. А что скажет программист? А он для начала перепишет предыдующую систему уравнений в следующем виде:
И дальше постарается найти решение, которое меньше всего отклонится от заданных равенств. Давайте назовём вектор (x0,x1,x2) вектором i, (1,1,1) вектором j, а (y0,y1,y2) вектором b:
В нашем случае векторы i,j,b трёхмерны, следовательно, (в общем случае) решения этой системы не существует. Любой вектор (alpha\*i + beta\*j) лежит в плоскости, натянутой на векторы (i, j). Если b не принадлежит этой плоскости, то решения не существует (равенства в уравнении не достичь). Что делать? Давайте искать компромисс. Давайте обозначим через e(alpha, beta) насколько именно мы не достигли равенства:
И будем стараться минимизировать эту ошибку:
Очевидно, что ошибка минимизируется, когда вектор e ортогонален плоскости, натянутой на векторы i и j.
Иными словами: мы ищем такую прямую, что сумма квадратов длин расстояний от всех точек до этой прямой минимальна:
UPDATE: тут у меня косяк, расстояние до прямой должно измеряться по вертикали, а не ортогональной проекцией. Вот этот комментатор прав.
Совсеми иными словами (осторожно, плохо формализовано, но на пальцах должно быть ясно): мы берём все возможные прямые между всеми парами точек и ищем среднюю прямую между всеми:
Иное объяснение на пальцах: мы прикрепляем пружинку между всеми точками данных (тут у нас три) и прямой, что мы ищем, и прямая равновесного состояния есть именно то, что мы ищем.
Минимум квадратичной формы
Итак, имея данный вектор b и плоскость, натянутую на столбцы-векторы матрицы A (в данном случае (x0,x1,x2) и (1,1,1)), мы ищем вектор e с минимум квадрата длины. Очевидно, что минимум достижим только для вектора e, ортогонального плоскости, натянутой на столбцы-векторы матрицы A:
Иначе говоря, мы ищем такой вектор x=(alpha, beta), что:
Напоминаю, что этот вектор x=(alpha, beta) является минимумом квадратичной функции ||e(alpha, beta)||^2:
Тут нелишним будет вспомнить, что матрицу можно интерпретирвать в том числе как и квадратичную форму, например, единичная матрица ((1,0),(0,1)) может быть интерпретирована как функция x^2 + y^2:
Вся эта гимнастика известна под именем линейной регрессии.
Уравнение Лапласа с граничным условием Дирихле
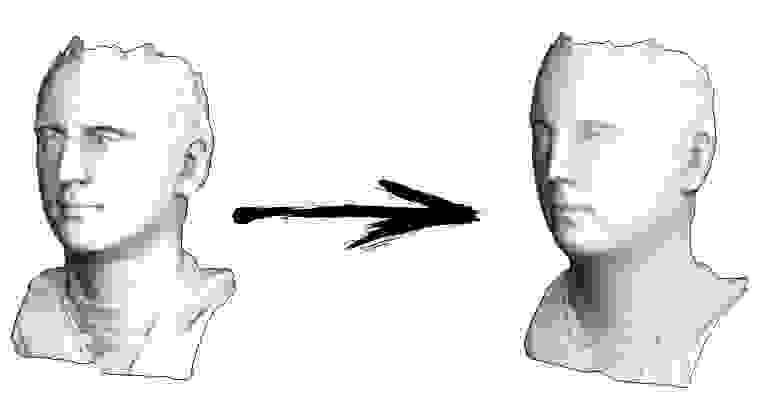
Теперь простейшая реальная задача: имеется некая триангулированная поверхность, необходимо её сгладить. Например, давайте загрузим модель моего лица:
Изначальный коммит доступен здесь. Для минимизации внешних зависимостей я взял код своего софтверного рендерера, уже подробно описанного на хабре. Для решения линейной системы я пользуюсь OpenNL, это отличный солвер, который, правда, очень сложно установить: нужно скопировать два файла (.h+.c) в папку с вашим проектом. Всё сглаживание делается следующим кодом:
X, Y и Z координаты отделимы, я их сглаживаю по отдельности. То есть, я решаю три системы линейных уравнений, каждое имеет количество переменных равным количеству вершин в моей модели. Первые n строк матрицы A имеют только одну единицу на строку, а первые n строк вектора b имеют оригинальные координаты модели. То есть, я привязываю по пружинке между новым положением вершины и старым положением вершины — новые не должны слишком далеко уходить от старых.
Ещё раз: переменными являются все вершины, причём они не могут далеко отходить от изначального положения, но при этом стараются стать похожими друг на друга.
Всё бы было хорошо, модель действительно сглажена, но она отошла от своего изначального края. Давайте чуть-чуть изменим код:
В нашей матрице A я для вершин, что находятся на краю, добавляю не строку из разряда v_i = verts[i][d], а 1000*v_i = 1000*verts[i][d]. Что это меняет? А меняет это нашу квадратичную форму ошибки. Теперь единичное отклонение от вершины на краю будет стоить не одну единицу, как раньше, а 1000*1000 единиц. То есть, мы повесили более сильную пружинку на крайние вершины, решение предпочтёт сильнее растянуть другие. Вот результат:
Давайте вдвое усилим пружинки между вершинами:
Логично, что поверхность стала более гладкой:
А теперь ещё в сто раз сильнее:
Что это? Представьте, что мы обмакнули проволочное кольцо в мыльную воду. В итоге образовавшаяся мыльная плёнка будет стараться иметь наименьшую кривизну, насколько это возможно, касаясь-таки границы — нашего проволочного кольца. Именно это мы и получили, зафиксировав границу и попросив получить гладкую поверхность внутри. Поздравляю вас, мы только что решили уравнение Лапласа с граничными условиями Дирихле. Круто звучит? А на деле всего-навсего одну систему линейных уравнений решить.
Уравнение Пуассона
Давайте ещё крутое имя вспомним.
Предположим, что у меня есть такая картинка:
Всем хороша, только стул мне не нравится.
Разрежу картинку пополам: 
И выделю руками стул:
Затем всё, что белое в маске, притяну к левой части картинки, а заодно по всей картинке скажу, что разница между двумя соседними пикселями должна равняться разнице между двумя соседними пикселями правой картинки:
Код и картинки доступны здесь.
Пример из жизни
Я специально не стал делать вылизанные результаты, т.к. мне хотелось всего-навсего показать, как именно можно применять методы наименьших квадратов, это обучающий код. Давайте я теперь дам пример из жизни:
У меня есть некоторое количество фотографий образцов ткани типа вот такой:
Моя задача сделать бесшовные текстуры из фотографий вот такого качества. Для начала я (автоматически) ищу повторяющийся паттерн:
Если я вырежу прямо вот этот четырёхугольник, то из-за искажений у меня края не сойдутся, вот пример четыре раза повторённого паттерна:
Вот фрагмент, где чётко видно шов:
Поэтому я вырезать буду не по ровной линии, вот линия разреза:
А вот повторённый четыре раза паттерн:
И его фрагмент, чтобы было виднее:
Уже лучше, рез шёл не по прямой линии, обойдя всякие завитушки, но всё же шов виден из-за неравномерности освещения на оригинальной фотографии. Вот тут-то и приходит на помощь метод наименьших квадратов для уравнения Пуассона. Вот конечный результат после выравнивания освещения:
Текстура получилась отлично бесшовной, и всё это автоматически из фотографии весьма посредственного качества. Не бойтесь математики, ищите простые объяснения, и будет вам инженерное счастье.
Методы наименьших квадратов без слёз и боли
Итак, очередная статья из цикла «математика на пальцах». Сегодня мы продолжим разговор о методах наименьших квадратов, но на сей раз с точки зрения программиста. Это очередная статья в серии, но она стоит особняком, так как вообще не требует никаких знаний математики. Статья задумывалась как введение в теорию, поэтому из базовых навыков она требует умения включить компьютер и написать пять строк кода. Разумеется, на этой статье я не остановлюсь, и в ближайшее же время опубликую продолжение. Если сумею найти достаточно времени, то напишу книгу из этого материала. Целевая публика — программисты, так что хабр подходящее место для обкатки. Я в целом не люблю писать формулы, и я очень люблю учиться на примерах, мне кажется, что это очень важно — не просто смотреть на закорючки на школьной доске, но всё пробовать на зуб.
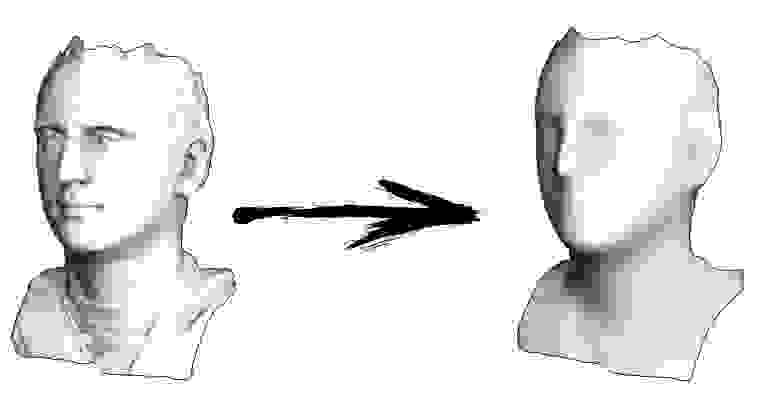
Итак, начнём. Давайте представим, что у меня есть триангулированная поверхность со сканом моего лица (на картинке слева). Что мне нужно сделать, чтобы усилить характерные черты, превратив эту поверхность в гротескную маску?
Пример 1: сглаживание данных
Давайте расскажу, как это работает. Начнём издалека, представьте, что у нас есть обычный массив f, например, из 32 элементов, инициализированный следующим образом:
А затем мы тысячу раз выполним следующую процедуру: для каждой ячейки f[i] мы запишем в неё среднее значение соседних ячеек: f[i] = ( f[i-1] + f[i+1] )/2. Чтобы было понятнее, вот полный код:
Каждая итерация будет сглаживать данные нашего массива, и через тысячу итераций мы получим постоянное значение во всех ячейках. Вот анимация первых ста пятидесяти итераций:
Если вам неясно, почему происходит сглаживание, прямо сейчас остановитесь, возьмите ручку и попробуйте порисовать примеры, иначе дальше читать не имеет смысла. Триангулированная поверхность ничем принципиально от этого примера не отличается. Представьте, что для каждой вершины мы найдём соседние с ней, посчитаем их центр масс, и передвинем нашу вершину в этот центр масс, и так десять раз. Результат будет вот таким:
Разумеется, если не остановиться на десяти итерациях, то через некоторое время вся поверхность сожмётся в одну точку ровно так же, как и в предыдущем примере весь массив стал заполнен одним и тем же значением.
Пример 2: усиление/ослабление характеристических черт
Полный код доступен на гитхабе, а здесь я приведу самую важную часть, опустив лишь чтение и запись 3Д моделей. Итак, триангулированная модель у меня представлена двумя массивами: verts и faces. Массив verts — это просто набор трёхмерных точек, они же вершины полигональной сетки. Массив faces — это набор треугольников (количество треугольников равно faces.size()), для каждого треугольника в массиве хранятся индексы из массива вершин. Формат данных и работу с ним я подробно описывал в своём курсе лекций по компьютерной графике. Есть ещё третий массив, который я пересчитываю из первых двух (точнее, только из массива faces) — vvadj. Это массив, который для каждой вершины (первый индекс двумерного массива) хранит индексы соседних с ней вершин (второй индекс).
Первое, что я делаю, это для каждой вершины моей поверхности считаю вектор кривизны. Давайте проиллюстрируем: для текущей вершины v я перебираю всех её соседей n1-n4; затем я считаю их центр масс b = (n1+n2+n3+n4)/4. Ну и финальный вектор кривизны может быть посчитан как c=v-b, это не что иное, как обычные конечные разности для второй производной.
Непосредственно в коде это выглядит следующим образом:
Ну а дальше мы много раз делаем следующую вещь (смотрите предыдущую картинку): мы вершину v двигаем v := b + const * c. Обратите внимание, что если константа равна единице, то наша вершина никуда не сдвинется! Если константа равна нулю, то вершина заменяется на центр масс соседних вершин, что будет сглаживать нашу поверхность. Если константа больше единицы (заглавная картинка сделана при помощи const=2.1), то вершина будет сдвигаться в направлении вектора кривизны поверхности, усиливая детали. Вот так это выглядит в коде:
Кстати, если меньше единицы, то детали будут наоборот ослабляться (const=0.5), но это не будет эквивалентно простому сглаживанию, «контраст картинки» останется:
Пример 3: добавляем ограничения
Давайте вернёмся к самому первому примеру, и сделаем ровно то же самое, но только не будем переписывать элементы массива под номерами 0, 18 и 31:
Остальные, «свободные» элементы массива я инициализировал нулями, и по-прежнему итеративно заменяю их на среднее значение соседних элементов. Вот так выглядит эволюция массива на первых ста пятидесяти итерациях:
Вполне очевидно, что на сей раз решение сойдётся не к постоянному элементу, заполняющему массив, а к двум линейным рампам. Кстати, действительно ли всем очевидно? Если нет, то экспериментируйте с этим кодом, я специально привожу примеры с очень коротким кодом, чтобы можно было досконально разобраться с происходящим.
Лирическое отступление: численное решение систем линейных уравнений.
Пусть нам дана обычная система линейных уравнений:
Её можно переписать, оставив в каждом из уравнений с одной стороны знака равенства x_i:
Пусть нам дан произвольный вектор 
Тогда, воткнув его в правую часть нашей системы, мы можем получить обновлённый вектор приближения решения 
Чтобы было понятнее, x1 получается из x0 следующим образом:
Повторив процесс k раз, решение будет приближено вектором
Давайте на всякий случай запишем рекурретную формулу:
При некоторых предположениях о коэффициентах системы (например, вполне очевидно, что диагональные элементы не должны быть нулевыми, т.к. мы на них делим), данная процедура сходится к истинному решению. Эта гимнастика известна в литературе под названием метода Якоби. Конечно же, существуют и другие методы численного решения систем линейных уравнений, причём значительно более мощные, например, метод сопряжённых градиентов, но, пожалуй, метод Якоби является одним из самых простых.
Пример 3 ещё раз, но уже с другой стороны
А теперь давайте ещё раз внимательно посмотрим на основной цикл из примера 3:
Я стартовал с какого-то начального вектора x, и тысячу раз его обновляю, причём процедура обновления подозрительно похожа на метод Якоби! Давайте выпишем эту систему уравнений в явном виде:
Потратьте немного времени, убедитесь, что каждая итерация в моём питоновском коде — это строго одно обновление метода Якоби для этой системы уравнений. Значения x[0], x[18] и x[31] у меня зафиксированы, соответственно, в набор переменных они не входят, поэтому они перенесены в правую часть.
Итого, все уравнения в нашей системе выглядят как — x[i-1] + 2 x[i] — x[i+1] = 0. Это выражение не что иное, как обычные конечные разности для второй производной. То есть, наша система уравнений нам просто-напросто предписывает, что вторая производная должна быть везде равна нулю (ну, кроме как в точке x[18]). Помните, я говорил, что вполне очевидно, что итерации должны сойтись к линейным рампам? Так именно поэтому, у линейной функции вторая производная нулевая.
А вы знаете, что мы с вами только что решили задачу Дирихле для уравнения Лапласа?
Кстати, внимательный читатель должен был бы заметить, что, строго говоря, у меня в коде системы линейных уравнений решаются не методом Якоби, но методом Гаусса-Зейделя, который является своебразной оптимизацией метода Якоби:
Пример 4: уравнение Пуассона
А давайте мы самую малость изменим третий пример: каждая ячейка помещается не просто в центр масс соседних ячеек, но в центр масс плюс некая (произвольная) константа:
В прошлом примере мы выяснили, что помещение в центр масс — это дискретизация оператора Лапласа (в нашем случае второй производной). То есть, теперь мы решаем систему уравнений, которая говорит, что наш сигнал должен иметь некую постоянную вторую производную. Вторая производная — это кривизна поверхности; таким образом, решением нашей системы должна стать кусочно-квадратичная функция. Проверим на дискретизации в 32 сэмпла:
При длине массива в 32 элемента наша система сходится к решению за пару сотен итераций. А что будет, если мы попробуем массив в 128 элементов? Тут всё гораздо печальнее, количество итераций нужно уже исчислять тысячами:
Метод Гаусса-Зейделя крайне прост в программировании, но малоприменим для больших систем уравнений. Можно попытаться его ускорить, применяя, например, многосеточные методы. На словах это может звучать громоздко, но идея крайне примитивная: если мы хотим решение с разрешением в тысячу элементов, то можно для начала решить с десятью элементами, получив грубую аппроксимацию, затем удвоить разрешение, решить ещё раз, и так далее, пока не достигнем нужного результата. На практике это выглядит следующим образом:
А можно не выпендриваться, и использовать настоящие солверы систем уравнений. Вот я решаю этот же пример, построив матрицу A и столбец b, затем решив матричное уравнение Ax=b:
А вот так выглядит результат работы этой программы, заметим, что решение получилось мгновенно:
Таким образом, действительно, наша функция кусочно-квадратичная (вторая производная равна константе). В первом примере мы задали нулевую вторую производную, в третьем ненулевую, но везде одинаковую. А что было во втором примере? Мы решили дискретное уравнение Пуассона, задав кривизну поверхности. Напоминаю, что произошло: мы посчитали кривизну входящей поверхности. Если мы решим задачу Пуассона, задав кривизну поверхности на выходе равной кривизне поверхности на входе (const=1), то ничего не изменится. Усиление характеристических черт лица происходит, когда мы просто увеличиваем кривизну (const=2.1). А если const Скрытый текст
Это результат по умолчанию, рыжий Ленин — это начальные данные, голубая кривая — это их эволюция, в бесконечности результат сойдётся в точку:
А вот результат с коэффицентом 2.:
Домашнее задание: почему во втором случае Ленин сначала превращается в Дзержинского, а затем снова сходится к Ленину же, но большего размера?
Заключение
Очень много задач обработки данных, в частности, геометрии, могут формулироваться как решение системы линейных уравнений. В данной статье я не рассказал, как строить эти системы, моей целью было лишь показать, что это возможно. Темой следующей статьи будет уже не «почему», но «как», и какие солверы потом использовать.
Кстати, а ведь в названии статьи присутствуют наименьшие квадраты. Увидели ли вы их в тексте? Если нет, то это абсолютно не страшно, это именно ответ на вопрос «как?». Oставайтесь на линии, в следующей статье я покажу, где именно они прячутся, и как их модифицировать, чтобы получить доступ к крайне мощному инструменту обработки данных. Например, в десяток строк кода можно получить вот такое: