в чем суть использования вероятности безошибочного прогноза
Оценка статистических параметров по выборочным данным
Представление средней арифметической выборки приводится обязательно с ее ошибкой.
Ошибка дисперсии вычисляется путем возведения в квадрат ошибки среднеквадратической.
Каждому значению доверительной вероятности соответствует свой уровень значимости (α). Он выражает вероятность нулевой гипотезы: вероятность того, что выборочная и генеральная средние не отличаются друг от друга. Иначе говоря, чем выше уровень значимости, тем меньше можно доверять утверждению, что различия существуют, т. е., он показывает, какой процент вариант совокупности (выборок) отвергают искомую статистическую закономерность. Уровень значимости 5 % (0,05) дополняет доверительную вероятность 95 % (0,95). В сумме они составляют 100 % (1). Если доказано подобие между выборками при α = 5 % (0,05), то из этого следует, что до 5 % вариант выборки подобие не подтверждают. В таблицах приложения приводятся численные значения для Р или α соответственно 0,95 и 0,99; 0,05 и 0,01. В этих случаях при интерпретации мы можем утверждать нулевую гипотезу (Н0). При более высоких уровне вероятности 0,99 и уровне значимости 0,01 мы получаем сильный довод для утверждения нулевой гипотезы.
Проверка статистических гипотез. Методологической основой любого исследования является формулировка рабочей гипотезы. В ходе исследования рабочая гипотеза либо принимается, либо отвергается. Статистической называют гипотезу о виде неизвестного распределения или о параметре распределения. Примеры гипотез:
· генеральная совокупность распределяется по закону Пуассона;
· средние арифметические двух совокупностей не равны между собой;
· дисперсии двух совокупностей равны между собой.
Выдвинутую гипотезу называют основной или нулевой (Н0). Гипотезу, которая противоречит нулевой, называют конкурирующей или альтернативной (Н1). Если нулевая гипотеза предполагает, что М = 20, то логическим отрицанием будет М ≠ 15. Простая гипотеза содержит одно предположение, сложная – состоит из конечного или бесконечного множества простых гипотез. Выдвинутую гипотезу проверяют на правильность ее статистическими методами, т. е. проводят статистическую проверку. При проверке могут быть допущены ошибки двух родов.
Ошибка первого рода – отвергается правильная гипотеза. Вероятность совершить ошибку первого рода называют уровнем значимости (α). Это значит, что в 5 случаях из 100 мы рискуем допустить ошибку первого рода.
Ошибка второго рода – принимается неправильная гипотеза, значимость ошибки которой допускается 0,95 и обозначается символом Р. Это значит, что в 95 случаях из 100 мы рискуем допустить ошибку второго рода.
Для проверки нулевых гипотез используют статистические критерии. При сравнении дисперсий используют критерий Фишера. В большинстве исследований для статистической проверки гипотез существенности различий средних арифметических используют параметрический критерий Стьюдента. Если нулевая гипотеза принимается, это не означает ее доказательство. Доказать на основании однократной или косвенной проверки гипотезу нельзя, а опровергнуть можно. Для повышения точности статистических данных необходимо уменьшить вероятности ошибок первого и второго рода, увеличить объем выборок. Область применения того или иного критерия задается законом его распределения.
Оценка точности опыта. При исследованиях методического характера необходимо приводить их оценку по показателю точность опыта (р). Его смысл состоит в установлении величины ошибки среднего арифметического ( mM ) в процентах от величины среднего арифметического (М).
Опыт считается достаточно точным, если р Пример. Среднее арифметическое общей биомассы многолетних трав в луговом ландшафте прирусловой поймы М = 235 ц/г, ошибка средней арифметической m M = ± 4 ц/га, N = 20. Используя формулу (1.15), выполним расчет показателей:
р = (4 / 235) · 100 = 1,7 %.
Полученная величина точности опыта достаточно точная.
Определение ошибки репрезентативности (m)
Ошибка репрезентативности (m) показывает, насколько результаты полученные при выборочном исследовании, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования (генеральная совокупность).
Взаимосвязь объёма выборки и репрезентативности
· Репрезентативность не зависит от объема выборки. Репрезентативность достигается только тогда, когда в выборку отобраны объекты из разных групп, при условии, что их доли в генеральной и выборочной совокупности равны. Репрезентативность выборки зависит только от методики отбора единиц из генеральной совокупности в выборочную совокупность и не зависит от объема. Конечно, чем больше объем выборки, тем выше ее точность, однако, неверно распределенная выборка в 5000 единиц намного хуже, чем хорошо распределенная выборка в 500 единиц.
· Чем более однородна генеральная совокупность, тем меньший объем выборочной совокупности потребуется для получения точных результатов. Если, например, в генеральной совокупности все респонденты имеют одинаковый доход, то будет достаточно опросить одного респондента, чтобы узнать средний доход по совокупности. Чтобы определить вкус каши достаточно съесть одну ложку, а не всю тарелку, конечно, при условии, что каша хорошо перемешана.
При правильно составленной выборочной совокупности можно получить достаточно полное представление о закономерностях, присущих всей генеральной совокупности. Основным правилом составления выборочной совокупности является обеспечение ее репрезентативности, т.е. соответствия данных выборочной и генеральной совокупностей.
Выборочная совокупность должна быть представительной или репрезентативной (способность быть отражением генеральной совокупности), для чего необходимы следующие требования:
· обладать характерными чертами генеральной совокупности, т.е. по составу быть максимально похожей на неё;
· достаточной по объему, т.е. по числу наблюдений.
Формула ошибки репрезентативности (m) для относительных величин:


Р – величина показателя;
q=100–P, если показатель рассчитан на 100;
q=1000 –P, если показатель вычислен на 1000, и т.д.;
n – число наблюдений.
Например: работающих на предприятии – 1400 человек (n), имеющих гипертоническую болезнь (ГБ) – 44 человека.
Показатель заболеваемости ГБ


Вывод: результаты выборочной совокупности по определению ГБ на предприятии отличаются от генеральной совокупности на ± 0,46 (средняя ошибка ± 0,46).
Формула (m) для средней величины: 

Например, у 49 больных (n) гастритом уровень пепсина М=1,0 г%, σ = ±0,35 г%

Вывод: результаты выборочной совокупности по определению уровня пепсина у 49 больных гастритом отличаются от генеральной совокупности (если бы исследования проводились у всех больных гастритом) на ± 0,05 (средняя ошибка ± 0,05).
Примечание: среднее квадратическое отклонение (σ)характеризует степень рассеивания вариант вокруг средней арифметической (смотри тему №3). Вычисляют по формуле:
Амплитуда ряда (см. тему №4)
К – «коэффициент К», (см. приложение №3).
Доверительные границы (М, P) средних и относительных величин –это границы относительных или средних величин размеров признака выход за пределы которых, вследствие случайных колебаний, имеет незначительную вероятность.
Доверительные границы для средней величины по формуле:
Мген., выб. – доверительные границы средней величины генеральной и выборочной совокупности,
t – доверительный критерий (устанавливается исследователем, но должен быть не меньше 2, смотри ниже),
m – ошибка репрезентативности.
Доверительные границы для относительной величины по формуле:
Pген.,выб. – доверительные границы относительной величины генеральной и выборочной совокупности;
t – доверительный критерий (устанавливается исследователем, но должен быть не меньше 2, смотри ниже);
m – ошибка репрезентативности.
Δ = tm (максимально возможная погрешность оценки генеральной совокупности),
t – доверительный критерий (устанавливается исследователем, но должен быть не меньше 2, смотри ниже);
m – ошибка репрезентативности.
Вероятность безошибочного прогноза (p) – это вероятность, с которой можно утверждать, что в генеральной совокупности относительных или средних величин (P, M) показатели будут находиться в пределах ±tm. Для медицинских исследований степень вероятности безошибочного прогноза (p) должна быть не менее 95%, т.е отображать объективную реальность проведенных исследований на 95%, тогда t=2 (см. ниже).
Зависимость доверительного критерия от степени вероятности безошибочного прогноза p (при n>30)
Таблица 5.1
| Степень вероятности (p) | Доверительный критерий (t) | |||||||||||||||
| 95,0% | ||||||||||||||||
| 99,0% | ||||||||||||||||
 n=49,p=95% (t=2), М=1,0г%,m=±0,05% Доверительные границы Мген.= Мвыб.± tm, отсюда Мген =1+2×0,05 не менее 1 г% – 0,1 г% = 0,9% Вывод: Установлено с вероятностью безошибочного прогноза 95% средний уровень пепсина в генеральной совокупности у больных гастритом не превышает 1,1 г% и не ниже 0,9 г%. При сопоставлении двух сравниваемых величин необходимо не только определить их разность, но и оценить достоверность, т.е. достоверно или случайно их различие. Проект Extra.imВ практической и научно-практической работе врачи обобщают результаты, полученные как правило на выборочных совокупностях. Для более широкого распространения и применения полученных при изучении репрезентативной выборочной совокупности данных и выводов надо уметь по части явления судить о явлении и его закономерностях в целом. Учитывая, что врачи, как правило, проводят исследования на выборочных совокупностях, теория статистики позволяет с помощью математического аппарата (формул) переносить данные с выборочного исследования на генеральную совокупность. При этом врач должен уметь не только воспользоваться математической формулой, но сделать вывод, соответствующий каждому способу оценки достоверности полученных данных. С этой целью врач должен знать способы оценки достоверности. Применяя метод оценки достоверности результатов исследования для изучения общественного здоровья и деятельности учреждений здравоохранения, а также в своей научной деятельности, исследователь должен уметь правильно выбрать способ данного метода. Среди методов оценки достоверности различают параметрические и непараметрические. Параметрическими называют количественные методы статистической обработки данных, применение которых требует обязательного знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров. Непараметрическими являются количественные методы статистической обработки данных, применение которых не требует знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров. Как параметрические, так и непараметрические методы, используемые для сравнения результатов исследований, т.е. для сравнения выборочных совокупностей, заключаются в применении определенных формул и расчете определенных показателей в соответствии с предписанными алгоритмами. В конечном результате высчитывается определенная числовая величина, которую сравнивают с табличными пороговыми значениями. Критерием достоверности будет результат сравнения полученной величины и табличного значения при данном числе наблюдений (или степеней свободы) и при заданном уровне безошибочного прогноза. Таким образом, в статистической процедуре оценки основное значение имеет полученный критерий достоверности, поэтому сам способ оценки достоверности в целом иногда называют тем или иным критерием по фамилии автора, предложившего его в качестве основы метода.
При проведении выборочных исследований полученный результат не обязательно совпадает с результатом, который мог бы быть получен при исследовании всей генеральной совокупности. Между этими величинами существует определенная разница, называемая ошибкой репрезентативности, т.е. это погрешность, обусловленная переносом результатов выборочного исследования на всю генеральную совокупность.
Формулы определения доверительных границ представлены следующим образом: Данный способ применяется в тех случаях, когда по результатам выборочной совокупности необходимо судить о размерах изучаемого явления (или признака) в генеральной совокупности. Обязательным условием для применения способа является репрезентативность выборочной совокупности. Для переноса результатов, полученных при выборочных исследованиях, на генеральную совокупность необходима степень вероятности безошибочного прогноза (Р), показывающая, в каком проценте случаев результаты выборочных исследований по изучаемому признаку (явлению) будут иметь место в генеральной совокупности. При определении доверительных границ средней величины или относительного показателя генеральной совокупности, исследователь сам задает определенную (необходимую) степень вероятности безошибочного прогноза (Р). Для большинства медико-биологических исследований считается достаточной степень вероятности безошибочного прогноза, равная 95%, а число случаев генеральной совокупности, в котором могут наблюдаться отклонения от закономерностей, установленных при выборочном исследовании, не будут превышать 5%. При ряде исследований, связанных, например, с применением высокотоксичных веществ, вакцин, оперативного лечения и т.п., в результате чего возможны тяжелые заболевания, осложнения, летальные исходы, применяется степень вероятности Р = 99,7%, т.е. не более чем у 1% случаев генеральной совокупности возможны отклонения от закономерностей, установленных в выборочной совокупности. Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия t, зависящее также и от числа наблюдений. При n>30 степени вероятности безошибочного прогноза Р = 99,7% — соответствует значение t = 3, а при Р = 95,5% — значение t = 2. При п
Данный способ применяется в тех случаях, когда необходимо определить, случайны или достоверны (существенны), т.е. обусловлены какой-то причиной, различия между двумя средними величинами или относительными показателями. Обязательным условием для применения данного способа является репрезентативность выборочных совокупностей, а также наличие причинно-следственной связи между сравниваемыми величинами (показателями) и факторами, влияющими на них. Формулы определения достоверности разности представлены следующим образом:
Если вычисленный критерий t более или равен 2 (t ≥ 2), что соответствует вероятности безошибочного прогноза Р равном или более 95% (Р ≥ 95%), то разность следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что будет иметь место и в генеральной совокупности. При t Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99,7%, следовательно можно утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч работы не случайно, а достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.
на оценку достоверности разности относительных показателей Условие задачи: при медицинском осмотре детей 3 летнего возраста в 18% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 4-летнего возраста составила 24% (m = ± 2,64%). Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп. Решение. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения. Под ред. чл.-корр. РАМН, проф. В.З.Кучеренко. М., «Гэотар-Медиа», 2007, учебное пособие для вузов Определение доверительных границ средних и относительных величин.Формулы определения доверительных границ представлены следующим образом: · для средних величин (М): Мген=Мвыб ± tm · для относительных показателей (Р): Рген=Рвыб ± tm Мвыб и Рвыб – значения средней величины и относительного показателя выборочной совокупности; m- ошибка репрезентативности; t— критерий достоверности (доверительный коэффициент). Данный способ применяется в тех случаях, когда по результатам выборочной совокупности необходимо судить о размерах изучаемого явления (или признака) в генеральной совокупности. Обязательным условием для применения способа является репрезентативность выборочной совокупности. Для переноса результатов, полученных при выборочных исследованиях, на генеральную совокупность необходима степень вероятности безошибочного прогноза (Р), показывающая, в каком проценте случаев результаты выборочных исследований по изучаемому признаку (явлению) будут иметь место в генеральной совокупности. При определении доверительных границ средней величины или относительного показателя генеральной совокупности, исследователь сам задает определенную (необходимую) степень вероятности безошибочного прогноза (Р). Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия t, зависящее также и от числа наблюдений. ТогдаМген=Мвыб± tm =80±2х1=80±2 удара в мин. Вывод: установлено с вероятностью безошибочного прогноза Р= 95%, что средняя частота пульса в генеральной совокупности, т.е. у всех водителей сельскохозяйственных машин, через 1 час работы в аналогичных условиях будет находиться в пределах от 78 до 82 ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в минуту возможна не более, чем у 5% случаев генеральной совокупности. на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности (Рген) Условие задачи: при медицинском осмотре 164 детей 3-х летнего возраста, проживающих в одном из районов г. Н, в 18% случаев обнаружено нарушение осанки функционального характера. Задание: определить ошибку репрезентативности (mР) и доверительные границы относительного показателя генеральной совокупности (Р ген). Вычисление ошибки репрезентативности относительного показателя: 2. Вычисление доверительных границ средней величины генеральной совокупности (Рген): производится следующим образом: а) необходимо задать степень вероятности безошибочного прогноза (Р =95%). б) при заданной степени вероятности и числе наблюдений больше 30, величина критерия tравна2 (t=2). ТогдаРген=Рвыб± tm =18%±2х3 = 18%±6%. Вывод: установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у детей 3-х летнего возраста, проживающих в г. Н., будет находиться в пределах от 12% до 24% случаев. Оценка достоверности статистических величин.При сплошном методе объектом исследования является вся совокупность единиц, представляющих изучаемое явление, которая называется генеральной совокупностью. Однако, поскольку сплошное исследование является трудоемким и дорогостоящим, при проведении медико-биологических статистических исследований чаше всего используется выборочный метод. При этом исследование проводится на выборочной совокупности, являющейся частью генеральной совокупности, отобранной для обследования и изучения. При проведении выборочного исследования обязательным является соблюдение следующих требований: 1) репрезентативность выборочной совокупности; 2) достаточное число единиц наблюдений выборочной совокупности. Для соблюдения первого требования, репрезентативности, очень важен способ отбора части единиц наблюдений из генеральной совокупности. Статистикой выработан ряд способов осуществления выборки. 1. Случайный отбор, основу которого составляет отбор единиц наблюдений путем жеребьевки. При этом для каждой единицы обеспечивается равная возможность попасть в выборку. 2. Механический отбор, при котором единицы генеральной совокупности последовательно расположенные по какому-либо признаку (по алфавиту, по датам обращения к врачу и т.д.), механически разбиваются на равные части. Из каждой части в заранее обусловленном порядке отбирают каждую пятую, десятую или какую-либо иную единицу наблюдения таким образом, чтобы обеспечить необходимый объем выборки. 3. Типический (типологический) отбор предполагает обязательное предварительное расчленение генеральной совокупности на отдельные качественно однородные группы (типы). Выборка, произведенная в случайном порядке в каждой из установленных типических групп, и будет называться типической. 4. Серийный (гнездный) отбор предполагает выборку из генеральной совокупности не отдельных единиц, а целых серий групп единиц, которые отбираются по принципам случайного или механического отбора. Серийный отбор очень удобен в практическом отношении, хотя точность его результатов уступает другим методам отбора. При выборе единиц наблюдения любым из перечисленных способов, возможны ошибки смещения, т.е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объективными и закономерными. При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки. Такие ошибки носят название случайных ошибок репрезентативности (m), и являются Фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на генеральной совокупности. На практике для определения средней ошибки выборки при проведении статистических исследований, используются следующие Формулы: 1) для расчета ошибки репрезентативности (mм) средней арифметической величины (М): 2) для расчета ошибки репрезентативности (mР) относительной величины (Р): В клинических и экспериментальных работах довольно часто приходится использовать малую выборку, когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, число наблюдений уменьшается на единицу, т.е. Знание величины ошибки недостаточно для того, чтобы быть уверенным в результатах выборочного исследования, так как конкретная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности. Для определения точности, с которой исследователь желает получить результат, в статистике используется такое понятие, как вероятность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований. Обычно, при проведении медико-биологических статистических исследований используют вероятность безошибочного прогноза 95% или 99%. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7% Определенной степени вероятности безошибочного прогноза соответствует определенная величина предельной ошибки случайной выборки (Δ) Определяется эта величина по формуле: Используя предельную ошибку выборки (Δ), можно определить доверительные границы, в которых с определенной вероятностью безошибочного прогноза заключено действительное значение статистической величины, характеризующей всю генеральную совокупность (средней или относительной). Для определения доверительных границ используются следующие Формулы: 1) для средних величин: 2) для относительных величин: При малом числе наблюдений (n 2 * σ 2 | ||||||||||||||||
| Δ 2 | ||||||||||||||||
2) для относительных величин:
Величина Δ определяется исследователем на основании необходимой вероятности безошибочного прогноза. Среднее квадратическое отклонение (σ) и относительная величина (Р) определяются либо на основании ранее проведенных исследований, либо на основании имеющихся данных литературы.


 не более 1 г% + 0,1% = 1,1 г%
не более 1 г% + 0,1% = 1,1 г% М
М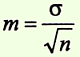
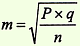
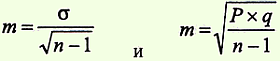
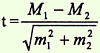
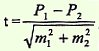
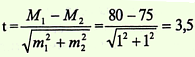
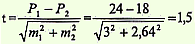
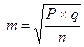 =
= 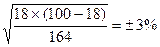
 ,
,  .
. ,где
,где  — доверительные границы средней величины в генеральной совокупности;
— доверительные границы средней величины в генеральной совокупности; — средняя величина, полученная при проведении исследования на выборочной совокупности;
— средняя величина, полученная при проведении исследования на выборочной совокупности; , где
, где  — доверительные границы относительной величины в генеральной совокупности;
— доверительные границы относительной величины в генеральной совокупности; — относительная величина, полученная при проведении исследования на выборочной совокупности;
— относительная величина, полученная при проведении исследования на выборочной совокупности;