в чем суть геометрии лобачевского
Модели геометрии Лобачевского
Задача
Геометрия Лобачевского — это такая геометрия, в которой не выполняется пятый постулат Евклида, аксиома параллельных. Вместо него принимается, что существует бесконечно много прямых, проходящих через не лежащую на прямой l точку и не пересекающих l. Геометрию Лобачевского можно реализовать на обычной евклидовой плоскости.
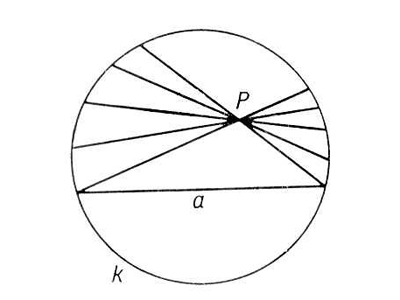
Примером служит модель Пуанкаре в круге. «Плоскостью» в этой модели называется внутренность обычного круга радиуса 1, а «прямыми» — дуги окружностей, перпендикулярных границе этого круга (окружности называются перпендикулярными, если перпендикулярны их касательные в точках пересечения). Граница круга называется абсолютом и считается не принадлежащей плоскости. Легко видеть, что через точку A, не лежащую на прямой l, действительно можно провести множество прямых, не пересекающих l. Все они находятся внутри угла, образованного прямыми a и b. Параллельными в смысле Лобачевского называются прямые, имеющие общую точку на абсолюте. Например, прямые l и a параллельны между собой. Прямые l и b тоже параллельны между собой (но при этом прямые a и b не параллельны).
Между точками плоскости Лобачевского можно вычислить расстояние. Если Q, R — точки на плоскости, а P, S — точки, в которых прямая, проходящая через Q и R, пересекает абсолют, то расстояние на плоскости Лобачевского между Q и R равно
где PR и т. д. — обычные расстояния между двумя точками.
Впрочем, эта страшная формула для решения задачи не понадобится. Однако важно представлять себе в общих чертах, как устроены расстояния в геометрии Лобачевского. Параллельные прямые, как хорошо видно на рисунке, бесконечно сближаются друг с другом с одного конца и бесконечно отдаляются с другого. Если же прямые не пересекаются и не параллельны, то точки, двигающиеся по этим прямым к абсолюту, всегда бесконечно отдаляются друг от друга. Вообще, при приближении к абсолюту точка бесконечно удаляется от центра круга.
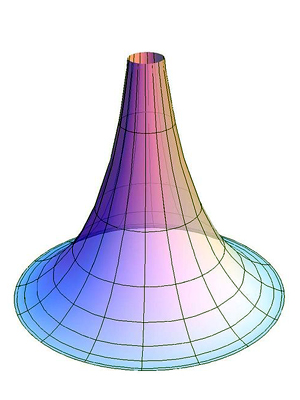
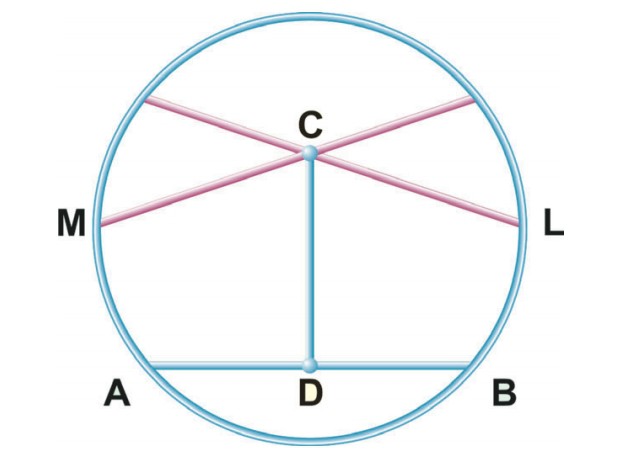
Другая реализация геометрии Лобачевского возможна на специальной поверхности в трехмерном пространстве — псевдосфере. Псевдосфера — поверхность вращения кривой \( z = \ln \left( \text
Псевдосфера, однако, не находится в однозначном соответствии со всей плоскостью Лобачевского в модели Пуанкаре. Во-первых, у псевдосферы есть граница, проходящая по плоскости z = 0. Во-вторых, у псевдосферы не такая топология, как у плоскости Лобачевского в модели Пуанкаре. Чтобы пояснить это утверждение, рассмотрим замкнутую кривую, делающую один оборот по псевдосфере вокруг оси Oz. Ясно, что никакими деформациями эта кривая не может быть стянута в точку: что бы мы ни делали, кривая всегда будет делать один оборот вокруг Oz (то есть кривую можно как угодно двигать по псевдосфере, можно изгибать ее, но нельзя допускать разрывов). Однако в модели Пуанкаре любая замкнутая кривая может быть непрерывно деформирована в точку! Разгадка состоит в том, что геометрия на псевдосфере лишь локально реализует геометрию Лобачевского. Это значит, что если вырезать кусок псевдосферы, в котором не будет отверстий, то ему можно будет однозначно сопоставить кусок плоскости Лобачевского из модели Пуанкаре, причем расстояние Лобачевского между любыми точками будет сохраняться. (Между евклидовой плоскостью и плоскостью Лобачевского нельзя построить даже локального соответствия, сохраняющего расстояния.)
Таким образом, псевдосфера состоит из кусков плоскости Лобачевского, гладко переходящих друг в друга. Как выполнить явное построение псевдосферы на основе модели Пуанкаре в круге? Другими словами, как склеить псевдосферу из одной или нескольких областей плоскости Лобачевского?
Подсказка 1
Конус и цилиндр — поверхности, на которых локально реализуется евклидова геометрия. Однако, разумеется, ни конус, ни цилиндр не являются целой евклидовой плоскостью. Как, имея в распоряжении лист бумаги (евклидову плоскость), построить цилиндр или конус?
Подсказка 2
Как уже было сказано, сечения псевдосферы плоскостями, проходящими через ее ось симметрии, являются геодезическими, то есть прямыми. Обратите внимание: во-первых, псевдосфера бесконечна вверх. Во-вторых, она бесконечно сужается при движении вдоль оси симметрии. Это значит, что все прямые, о которых говорилось двумя строками выше, бесконечно сближаются (но не пересекаются), то есть параллельны. На псевдосфере, таким образом, есть целое семейство параллельных прямых.
Решение
Оказывается, что псевдосфера — аналог конуса, склеенного из евклидовой плоскости. Она получается из области, лежащей между двумя параллельными в смысле Лобачевского прямыми, склеиванием по этим прямым. Действительно, разрежем псевдосферу плоскостью, проходящей через ее ось симметрии. Тогда у каждой из полученных частей границами являются пары прямых, которые, как уже было отмечено в подсказке, параллельны. Если же сделать не два разреза, а один, то получится всего одна область, ограниченная двумя параллельными «лучами» Лобачевского a, b и кривой c, которая в трехмерном пространстве является окружностью. Эта область является разверткой псевдосферы; точно так же как сектор окружности в евклидовой плоскости — развертка конуса.
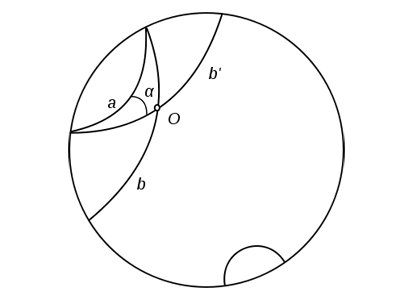
Рис. 3. На обоих рисунках серым цветом выделена одна и та же область плоскости Лобачевского. Слева она изображена в модели Пуанкаре, справа она вложена в трехмерное пространство. Область ограничена линиями a, b и c. a и b — лучи Лобачевского, перпендикулярные c, а c — отрезок орицикла. В модели Пуанкаре орицикл является окружностью, которая касается абсолюта
Из симметрии очевидно, что c перпендикулярна всему семейству параллельных прямых на псевдосфере. Кривая, обладающая таким свойством, носит в геометрии Лобачевского специальное название: орицикл. Чем же орицикл является в модели Пуанкаре? В евклидовой геометрии, разумеется, семейству параллельных прямых перпендикулярно другое семейство параллельных прямых. В геометрии Лобачевского это не так: кривая c, конечно, прямой не является. Впрочем, не составляет труда выяснить вид c в модели Пуанкаре. В этом помогает замечательный факт: евклидовы углы в модели Пуанкаре совпадают с углами плоскости Лобачевского. Поэтому задача сводится к следующей: найти кривую, перпендикулярную семейству касающихся друг друга в одной точке окружностей. У этой кривой нужно будет выбрать отрезок, равный по длине окружности основания псевдосферы.
Такой кривой является любая окружность, перпендикулярная общей касательной семейства и проходящая через точку касания. Отсюда немедленно следует, что эта окружность будет касаться абсолюта.
Таким образом, орицикл в модели Пуанкаре — любая окружность, касающаяся абсолюта, а развертка псевдосферы состоит из двух лучей и части орицикла. В некотором смысле это — «треугольник» с двумя прямыми углами. Следует подчеркнуть: пара «лучей» и отрезок могут быть выбраны произвольным образом, с условием, что лучи параллельны (в смысле Лобачевского) друг другу, перпендикулярны отрезку, а отрезок имеет заданную длину, а именно — 2π.
Интересно посмотреть, что будет, если отрезок c имеет длину, отличную от длины окружности в основании псевдосферы. В модели Пуанкаре это может соответствовать тому, что вместо b берется какая-нибудь другая прямая, параллельная а (например, одна из черных внутри серой области в левой части рис. 3).
Для понимания этого полезен тот факт, что плоскость Лобачевского однородна и изотропна. Из этого немедленно следует, что любую вырезанную часть псевдосферы можно, изгибая, свободно двигать по псевдосфере (возможно, с наложениями). Вырежем наш «прямоугольный треугольник» с конечным отрезком длины, меньшей 2π. Его можно двигать по псевдосфере вверх до тех пор, пока отрезок орицикла не сомкнется в окружность, а две границы не сольются. Таким образом, из такого треугольника получается псевдосфера, у которой отрезана нижняя часть.
Если же длина с больше 2π, то построить из такого треугольника фигуру вращения в евклидовом пространстве нельзя. Однако его можно разрезать на треугольники, у каждого из которых сторона будет меньше 2π, каждый из них разместить на псевдосфере и склеить между собой. Таким образом, треугольник будет «намотан» на псевдосферу. Наконец, саму псевдосферу можно склеить не из одного треугольника, а из нескольких (подумайте, как).
Послесловие
Кроме модели Пуанкаре и псевдосферы существуют и другие модели геометрии Лобачевского. Исторически первой появилась модель Клейна в круге. В ней прямыми называются не дуги окружностей, а хорды, а расстояние вычисляется по точно такой же формуле. Другая модель — тоже Пуанкаре, но в полуплоскости. Ее можно представлять себе как модель Пуанкаре, у которой радиус круга устремлен к бесконечности. Абсолют превращается в границу полуплоскости, прямые Лобачевского — в полуокружности, перпендикулярные абсолюту, либо в прямые, перпендикулярные абсолюту.
Попробуем взглянуть единым взглядом на все эти модели. Каждая модель состоит из нескольких обязательных «ингредиентов». Необходимо определить, во-первых, что такое сама плоскость Лобачевского. Это всегда некоторая двумерная поверхность, возможно вложенная в объемлющее пространство (как псевдосфера). Во-вторых — что такое прямые на этой плоскости Лобачевского. Это некоторые кривые на поверхности (мы каждый раз указывали, какие именно кривые принимаются за «прямые» в разных моделях). И, наконец, всегда должен быть какой-то способ определять расстояния на этой плоскости (так называемая метрика), причем так, чтобы прямая всегда была кратчайшим путем между двумя точками.
Нетрудно заметить, что эти «ингредиенты» немного избыточны в том смысле, что необходимо проверить, что прямая — действительно кратчайшее расстояние между двумя точками. Это вовсе не очевидно для формулы из условия:
Чтобы избавиться от этой избыточности, можно определять геометрию немного по-другому. А именно, будем задавать расстояния не между какими угодно двумя точками, а только между бесконечно близкими. После этого можно естественным образом определить длину кривой, разбив ее на малые части и просуммировав их длины (то есть взяв интеграл по кривой). Наконец, назовем отрезком прямой в этой геометрии линию, соединяющую две точки и имеющую кратчайшую длину.
Метрика полностью определяет внутренние свойства поверхности, в частности, насколько и каким образом эта поверхность искривлена. Таким образом, мы пришли к тому, с чего начали: геометрия Лобачевского — это геометрия искривленной поверхности, а именно — псевдосферы. А все модели геометрии Лобачевского — это разные системы координат, введенные на плоскости Лобачевского. Метрики моделей, разумеется, отличаются между собой, но при этом описывают одну и ту же геометрию.
Чтобы не быть голословными, выпишем явно метрики для евклидового пространства и геометрии Лобачевского. Начнем с модели Пуанкаре в верхней полуплоскости, потому что в ней сразу будут видны все особенности, характерные для искривленных поверхностей. Пусть две точки имеют координаты (x, y) и (x + dx, y + dy). Тогда квадрат расстояния между ними вычисляется по формуле
Для евклидовой плоскости вместо этого есть всем известная формула
\[ \mathrm
которая есть не что иное, как теорема Пифагора.
Метрики для модели Клейна и Пуанкаре можно при желании посмотреть, например, в Википедии (см. Beltrami–Klein model и Poincaré disk model).
Еще более глубокое изучение вопроса приведет нас к такому понятию, как кривизна пространства. Не вдаваясь в подробности, обратим внимание лишь на то, что поверхность может быть искривлена в каждой точке двумя качественно различными способами. В одном случае поверхность напоминает часть эллипсоида, и кривизна считается положительной. В другом случае поверхность похожа на седло, и ее кривизна отрицательна. Псевдосфера, как видно на ее изображении (а значит, и плоскость Лобачевского), имеет отрицательную кривизну, причем оказывается, что эта кривизна постоянна (не зависит от точки поверхности). Это, кстати, проясняет происхождение названия «псевдосфера»: обычная сфера является поверхностью с постоянной положительной кривизной.
Рис. 4. Слева направо: поверхность отрицательной кривизны (однополостный гиперболоид), поверхность нулевой кривизны (цилиндр) и поверхность положительной кривизны (сфера). Рисунок с сайта en.wikipedia.org
Геометрия Лобачевского, созданная в XIX веке, была важнейшей ступенью к созданию области математики, которая сейчас называется дифференциальной геометрией. Она занимается изучением произвольных искривленных пространств, а ее математический аппарат является фундаментом такой важной области современной физики, как общая теория относительности (ОТО). Дело в том, что, согласно ОТО, пространство-время, в котором мы живем, обладает кривизной, причем кривизна пространства соответствует наличию в этой точке пространства гравитационного поля.
ОТО подверглась многочисленным экспериментальным проверкам (см.: Столетие ОТО, или Юбилей Первой ноябрьской революции, «Элементы», 25.11.2015), а поправки, связанные с ней, приходится учитывать для точной спутниковой навигации. Кроме того, ей описывается физика массивных объектов, таких как обычные и нейтронные звезды, сверхновые и черные дыры (список можно продолжать). Наконец, ОТО лежит в основе современной науки о Вселенной — космологии.
Согласно здравому смыслу, а также всем имеющимся наблюдательным данным, Вселенная на больших масштабах однородна и изотропна. Это в любом случае означает, что она является пространством постоянной пространственной кривизны. В связи с этим с самых первых лет космологии рассматривались три возможности: плоская Вселенная, Вселенная положительной кривизны («сферическая Вселенная») и Вселенная отрицательной кривизны («Вселенная Лобачевского»). На данный момент, правда, считается, что кривизна Вселенной нулевая (в пределах современной точности измерений). Это находит объяснение в современной теории инфляции. Согласно последней, Вселенная в начальной стадии своей эволюции испытывала очень быстрое расширение и в результате увеличилась во много раз (это и называется инфляцией). Вполне возможно, что до инфляции Вселенная была сферической, «Вселенной Лобачевского» или имела какую-то другую сложную геометрию. Однако расширение привело к тому, что сейчас наблюдениям доступна лишь очень малая часть всей Вселенной, и ее геометрия должна быть неотличима от плоской.
Геометрия Лобачевского
Пятой аксиомой Евклида была аксиома о параллельных прямых, так называемый постулат о параллельных линиях, который гласит: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. То есть эта аксиома утверждает, что существует только одна прямая, проходящая через данную точку вне данной прямой и параллельной этой данной прямой.
Сложная формулировка пятого постулата Евклида о параллельных линиях породила множество гипотез и предположений о возможной зависимости его от других постулатов. Были предприняты многочисленные попытки вывести его из остальных аксиом геометрии, но, к сожалению, они оказались тщетны. Усилия доказать пятый постулат от противного также не увенчались успехом.
И все же, в начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Больяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.
Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в его именем.
Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского.
Аксиома параллельности Лобачевского выглядит следующим образом:
Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.
Непротиворечивость аксиомы доказывается представлением модели, в которой реализуются данные аксиомы.
Основы аналитической геометрии, заложенные Лобачевским, практически наметили необходимую для доказательства модель. Лобачевский заметил, что орисфера в пространстве изометрична евклидовой плоскости. Полностью реализовать модель смогли работы Клейна, Пуанкаре и других ученых.
Геометрия Лобачевского нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.
В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре, «неевклидова геометрия есть ключ к решению всей задачи».
Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел».
Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света:
В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская возможным тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.
«Он бросил вызов аксиоме»: 195 лет неевклидовой геометрии Лобачевского
«Он бросил вызов аксиоме»
Эйнштейн об открытии Н.И.Лобачевского.
195 лет назад (11 (23) февраля 1826 г.) на заседании физико-математического факультета Императорского Казанского университета Николай Иванович Лобачевский впервые представил общественности неевклидову геометрию.
Текст доклада «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных» не сохранился, но известно, что в этот день ученый изложил основы новой геометрии, в которой нарушались общепринятые представления, в частности пятый постулат Евклида, гласящий, что две прямые, пересекающие друг друга, не могут быть одновременно параллельны третьей прямой (прим.: постулат изложен в формулировке Джона Плейфэра). До Лобачевского евклидова геометрия считалась единственной и незыблемой.
Николай Лобачевский заменил пятый постулат Евклида на противоположное утверждение: если из точки, не лежащей на прямой, выпустить все лучи, пересекающие эту прямую, то слева и справа эти лучи будут ограничены двумя предельным лучами, которые прямую уже не пересекут, но будут становиться к ней все ближе и ближе, а угол между этими предельными лучами будет строго меньше 180 градусов; то есть через точку, не лежащую на данной прямой, можно провести не одну прямую, параллельную данной (как у Евклида), а сколько угодно, причем эти прямые будут вести себя иначе, чем в трактовке Евклида.
Справка. Обычно в современных изложениях геометрии 5-й постулат Евклида заменяется на эквивалентную ему аксиому параллельных прямых (встречается уже у Прокла в V в. н. э.): через точку, не лежащую на данной прямой, можно провести только одну прямую, не пересекающуюся с данной. (Слово «прямая» здесь, как обычно в современной математике, обозначает бесконечную прямую).
Высказанная ученым идея о сходимости параллельных прямых (две параллельные прямые могут сначала сближаться, а потом удаляться) не произвела на присутствующих должного впечатления. Революционную неевклидову геометрию в России не поняли, Академия наук дала отрицательную оценку, а в журнале «Сын отечества» язвительно написали, что в ней отсутствует не только ученость, но и элементарный здравый смысл.
«Николай Иванович Лобачевский был гениальным ученым. Он был необычайно упорен. Будучи уже ректором университета, Лобачевский слыл среди коллег сумасшедшим из-за того, что придумал свою неевклидову геометрию. Позднее он ее издал, но параллельно, когда до нее уже додумались и другие люди», — рассказывал в беседе с «Научной Россией» академик РАН Владимир Захаров.
Геометрия Лобачевского стала толчком к переосмыслению природы пространства. Можно сказать, что работа ученого подготовила условия для создания общей теории относительности, ведь раньше у нас была только одна геометрия и одно понимание пространства, но это в корне изменилось благодаря нашему соотечественнику.
Спустя три года после выступления в Казанском университете Лобачевский опубликовал статью о своей геометрии в университетском журнале. Как уже отмечалось выше, поначалу многие отнеслись к работе ученого критически; потребовались годы, чтобы неевклидова геометрия отвоевала себе место под Солнцем.
Неевклидова геометрия в каком-то смысле разделила науку на до и после, но эта работа отнюдь не единственный вклад Николая Лобачевского в развитие научной мысли. Независимо от бельгийского математика Жерминаля Данделена Лобачевский разработал метод приближенного решения уравнений, уточнил понятие непрерывной функции, написал работы о тригонометрических рядах, предложил признак сходимости числовых рядов и опубликовал немало других важных трудов.
Подготовлено по материалам:
● Н. И. Лобачевский, Геометрические исследования по теории параллельных линий. Перевод, комментарии, вступительные статьи и примечания профессора В. Ф. Кагана. М.-Л., изд-во Академии Наук СССР, 1945.
Николай Иванович Лобачевский и его вклад в науку
Геометрия Евклида
Проникновение геометрии в Древнюю Грецию превратило ее из эмпирической и установленной на глаз науки в цепь связанных между собой постулатов и аксиом, каждые из которых заняли определенное место в создаваемой строгой науке. Именно в Древней Греции геометрия приобрела тот современный вид, который мы помним из средней школы: каждое предположение логически вытекает из предыдущего, вместе с которым обусловливает последующее.
Нужно отметить, что, попав на благодатную почву, геометрия как наука стала бурно развиваться и даже превращаться в своеобразный культ. Каждая теорема, которую логически выводили на основании других, была маленькой победой человеческого ума, так как знания, полученные опытным путем, подтверждались строгими правилами. Ученые Древней Греции старались свести к необходимому минимуму те факты, которые устанавливают опытным путем, то есть созерцанием и наблюдением. Превратить геометрию в науку, каждое положение которой выводится по правилам логики, — вот какой была цель научной школы Платона. Согласно тенденциям этой школы любая научная дисциплина, в том числе и геометрия, должна выводиться или развиваться из как можно меньшего числа исходных положений, которые составляют костяк данной науки. Кроме этого, Платон и его последователи старались освободить изложение геометрии от наглядных выводов.
Центром интеллектуальной жизни греческого мира в конце 4 века до нашей эры стала Александрия. Именно здесь развернулась деятельность Евклида. Как раз его «Начала» буквально вытеснили все руководства по геометрии, существовавшие ранее. Все прежние сочинения были полностью забыты, более того — потеряны, как только появилось это руководство, содержащее основы геометрии. Именно эта работа затем властвовал на протяжении более двух тысяч лет везде, где преподавали геометрию.
Фундаментальный и основополагающий труд Евклида состоит из тринадцати книг и предлагает значительный объем знаний — от учения о параллельных линиях до теоремы Пифагора.
Любой современный человек, ознакомившись с трудами «Начала», с удивлением обнаружит, что многое, что содержится там, он когда-то узнал в школе. Немало формулировок отдельных теорем, построений и доказательств сохранили свое значение и сегодня и приводятся в современных книгах практически в оригинальном виде.
Книги Евклида построены по одному принципу — вначале располагаются аксиомы и постулаты, которые служат для определения основ геометрии. До сих пор непонятна разница между аксиомами и постулатами, выдвинутыми в «Началах», однако последующие переиздания содержат пять главных постулатов.
Даже неспециалист увидит, что последний постулат отличен от других. Если предыдущие четыре достаточно понятны, наглядны и их практически невозможно оспорить, то пятый сразу же вызывает некое «отторжение».
Такая же ситуация возникла и после выхода «Начал». Уже через несколько столетий после издания этого труда безошибочность пятого постулата стали ставить под сомнение, поскольку он резко отличался от остальных более сложной формулировкой, а также отсутствием очевидности. Многие ученые заявляли, что пятый постулат — это теорема, которую сам Евклид так и не смог доказать. Более того, интересен факт, что именно пятый постулат условно делит геометрию на две части: абсолютную геометрию, где использовались доказательства на основании четырех постулатов, и собственно евклидову геометрию, полностью основанную на пятом постулате (каждое доказательство в этой части геометрии опирается на него).
В итоге было решено доказать ее вместо Евклида, опираясь на остальные постулаты и аксиомы, приведенные в «Началах». Решение этой задачи пытались найти более сотни ученых-геометров. Однако во всех случаях предложенные доказательства содержали либо грубые очевидные ошибки, либо глубоко скрытые неточности. Со временем пятый постулат заменили более простой формулировкой, однако сама по себе проблема оставалась нерешенной. В школьных учебниках пятый постулат Евклида обычно описывается как более «очевидная» аксиома: «На плоскости через точку, лежащую вне прямой, проходит только одна параллель к этой прямой».
«Очевидность» этой аксиомы означает, что ее можно доказать, если принять пятый постулат. Или если заменить этой аксиомой классическую формулировку пятого постулата, то он также может быть доказан. Однако доказать верность без использования таких «уловок» не удавалось. В итоге еще в начале XIX века проблема параллелей оставалась нерешенной.
Геометрия Лобачевского
Разрешить проблему параллелей удалось русскому математику Николаю Ивановичу Лобачевскому. Однако доказательство было выполнено косвенно. Он просто допустил, что пятый постулат неверен, и на основании этого вывел новую (так называемую не евклидову) геометрию. Тот факт, что новая геометрия непротиворечива, удалось доказать лишь спустя тридцать лет. Отсюда следует, что проблема параллелей снимается сама собой.
Лобачевский вместо пятого постулата сформулировал новую аксиому параллельных прямых, которая по смыслу оказалась прямо противоположна пятому постулату Евклида:
Через точку вне прямой можно провести не одну прямую, не встречающуюся с данной прямой, а по крайней мере две.
На основании этой теоремы и остальных четырех постулатов абсолютной геометрии Лобачевский и получил свою, которая была так же логически безупречна, как и геометрия Евклида.
Аксиома Лобачевского на первый взгляд может показаться абсурдной или как минимум странной. Кажется, что он подменяет очевидное неочевидным, противоречит установившимся геометрическим представлениям. Но если этот вопрос рассмотреть глубже, то неочевидность именно пятого постулата Евклида будет налицо.
Так, если внимательно прочитать первые четыре постулата Евклида, можно заметить, что они относятся к фигурам ограниченного размера, а пятый — нет. Он оперирует неограниченной, бесконечной прямой. В итоге если мы захотим проверить правильность данного постулата на практике, то не сможем это сделать, поскольку такой эксперимент осуществить невозможно. Можно представить следующую ситуацию. Например, если предположить, что угол MCL очень маленький, а затем продлить отрезки CL и AB, то, даже обладая необширной фантазией, можно представить, что при таких условиях эти прямые не пересекутся даже на расстоянии, выходящем за пределы нашей планеты! В то же время если взять какую-либо ограниченную часть пространства, например круг, то каким бы большим он ни был, мы можем провести множество прямых, проходящих через точку С и не пересекающих прямую AB.
Поэтому нет никаких оснований считать утверждение Лобачевского неправильным.
Отличие двух противоположных по своей сути предположений заключается только в том, что евклидов постулат более понятен человеческому сознанию.
Он соответствует нашему обыденному восприятию, в конце концов мы к нему привыкли… В этом случае можно вспомнить, что у древних было распространено представление, будто Земля плоская, а факт, что она круглая (как предполагала революционная гелиоцентрическая теория Коперника), полностью отрицался. Однако в отличие от теории Коперника, в которой говорилось об ином расположении и движении тел в пространстве, понимание идеи Лобачевского требует более абстрактного мышления.
Неудивительно, что свою геометрию Лобачевский назвал воображаемой, а Евклидову — употребительной, что подчеркивало ее более естественные основы. Более того, в поздних трудах для своей новой теории ученый применял термин «пангеометрия» (всеобщая геометрия). Такое название подчеркивало, что геометрия Евклида — всего лишь частный (предельный) случай геометрии Лобачевского.
Доказательства непротиворечивости геометрии Лобачевского
Не секрет, что геометрия Лобачевского не получила признания при его жизни из-за необычности. Более того, он был осмеян и к концу своих дней морально опустошен, так как считал, что теории суждено умереть вместе с создателем. Все осложнялось тем, что ученому не удалось найти объективных доказательств непротиворечивости своей теории. Для признания правоты Лобачевского потребовалось не только время, но и дальнейшее развитие математической науки, нахождение связей между различными ее разделами.
Теория Лобачевского прошла проверку временем и не оказалась пустышкой, которая, как думали его современники, в будущем сама уничтожит себя.
Фактический материал, который позволил устранить сомнения в непротиворечивости новой геометрии, был получен при разработке теории поверхностей. Если проследить за изменением свойств фигур, расположенных на изгибаемых поверхностях, то можно сделать некоторые неожиданные выводы. Сама теория поверхностей разрабатывалась немецким математиком Карлом Фридрихом Гауссом, а затем развивалась российским ученым Фердинандом Миндингом. Одним из главных понятий в теории поверхностей были так называемые геодезические линии, которые можно сравнить с обыкновенными прямыми на плоскости. И геодезические линии, и прямые выполняют одну и ту же функцию — определяют кратчайшее расстояние между точками. Разница лишь в том, что в искривленном пространстве геодезические линии представляют собой, грубо говоря, искривленные линии. Например, на сфере геодезическими линиями являются большие окружности, опоясывающие ее.
В результате Миндинг вывел формулы для геодезических треугольников (в них стороны образованы геодезическими линиями), которые совпали с планиметрией Лобачевского. Удивительно, но факт — доказательства непротиворечивости новой геометрии практически лежали на поверхности и существовали уже при жизни ученого. Однако ни один из математиков не заметил этого, так как они не были знакомы с работами друг друга. Потребовалось время, и только через 28 лет после открытия Миндинга (по прошествии 12 лет после смерти Лобачевского) итальянский геометр Эудженио Бельтрами сопоставил эти два исследования, провел строгие расчеты и вывел модель геометрии Лобачевского — три псевдосферические поверхности.
Таким образом и была убедительно доказана непротиворечивость, иными словами — верность геометрии Лобачевского. Она выражает свойства определенных криволинейных фигур в пространстве Евклида (таком, которое описывается аксиомами геометрии Евклида), а значит, не может быть противоречивой. Если бы она была таковой, то тогда геометрия Евклида противоречила бы сама себе, что не является истиной. Со временем было показано, что данная модель лишь частично доказывает непротиворечивость неевклидовой геометрии. Однако начало было положено.
Как только была доказана непротиворечивость геометрии Лобачевского, идеи на ее основе стали оказывать влияние на дальнейшее развитие математической науки.
Интересно, что вскоре была опубликована переписка Гаусса, в которой фигурировало его настоящее мнение о Лобачевском, скрываемое в годы непризнания неевклидовой геометрии. Ведь симпатия к ученому и его открытию тогда грозила всеобщим осмеянием.
Полная реабилитация Лобачевского дала импульс к появлению новых моделей неевклидовой геометрии, полностью подтверждающих непротиворечивость геометрии ученого.
Сферы применения неевклидовой геометрии Лобачевского
Практическое применение неевклидовой геометрии нашли только в конце XIX века. В конце труда «О началах геометрии» Лобачевский высказал мысль: «Оставалось бы исследовать, какого рода перемена произойдет от введения воображаемой геометрии в механику…» Непризнание его достижений оставляло мало надежды на то, что пожелания ученого сбудутся. Однако время расставило все точки над «i», его теория не только была признана верной, но и получила практическое применение.
Лобачевский показал, что в пределах Солнечной системы для расчетов достаточно применять простую евклидову геометрию. Свою геометрию он использовал для математического анализа, а точнее — для вычисления определенных интегралов. Будучи уверенным в верности собственной теории и в том, что классическая геометрия — частный (а вернее — предельный) случай неевклидовой геометрии, ученый был убежден, что его система имеет гораздо больший потенциал: она не может не описывать более глобальные закономерности природы.
После того как непротиворечивость геометрии Лобачевского была доказана, на нее обратили внимание самые выдающиеся математики того времени. В 1881-м на ее основе была создана новая дисциплина — теория автоморфных функций, построенная великим французским математиком и физиком Анри Пуанкаре, которая имеет огромное значение для фундаментальной науки.
Важное практическое приложение геометрии Лобачевского нашел русский физик Александр Фридман. Используя в 1922 году идеи теории относительности и решая уравнение Эйнштейна, он пришел к выводу, что Вселенная расширяется с течением времени.
Вскоре эта теория блестяще подтвердилась на практике, но уже, как это часто бывает, после смерти Фридмана. Наблюдения американского астронома Эдвина Хаббла подтвердили это. В 1929 году он, не знакомый с теорией Фридмана, обнаружил, что удаленные туманности как бы «разбегаются» в разные стороны. При этом скорость этого «разбегания» оказалась пропорциональна расстоянию между ними.
Следующим важным применением геометрии Лобачевского является то, что она оказалась естественной частью теории относительности.
Законы сложения относительных скоростей, полученные Альбертом Эйнштейном, напрямую связаны с геометрией Лобачевского.
А в 1950-х годах советский физик Н. А. Черников стал успешно использовать геометрию Лобачевского для исследования столкновений элементарных частиц в ускорителе, а также при изучении других вопросов физики элементарных частиц и ядерных реакций.
Все идеи, которые были выдвинуты на основании геометрии Лобачевского, описать практически невозможно. Многие еще только находятся на пути развития, и до их практического применения остается еще много времени. Однако сама фундаментальность открытия дает полную уверенность в том, что неевклидова геометрия будет приводить к новым изобретениям, так как потенциал ее безграничен.
Краткая биография
Николай Иванович Лобачевский родился 20 ноября (1 декабря) 1792 года в Нижнем Новгороде в семье чиновника. После смерти отца в 1800 году семья пере ехала в Казань, где Николай Лобачевский провел всю свою жизнь. Там он окончил гимназию, поступил в только что основанный Казанский императорский университет. За бойкий характер и неповиновение Лобачевского хотели исключить, однако он был на хорошем счету у многих преподавателей, что и спасло его. После окончания университета в 1811-м получил степень магистра по физике и математике с отличием, остался работать при университете и в 1816-м дослужился до профессора. Спустя четыре года после ревизорской проверки был назначен на должность декана физико-математического факультета, однако на продолжении семи лет не проявлял никакой творческой активности из-за тяжелой обстановки в университете. В течение этого времени написал две книги «Геометрия» и «Алгебра», которые так и не увидели свет.
23 (11) февраля 1826 года Лобачевский сделал первый доклад о новой «воображаемой геометрии». В 1827-м назначен ректором университета и с голо вой погрузился в хозяйственные дела — реорганизацию штата, строительство механических мастерских, лабораторий и обсерватории. В этот период Казанский императорский университет приобрел статус авторитетного и лучшего учебного заведения страны. При нем издавался научный журнал «Ученые записки Казанского университета». Лобачевский сам читал ряд спецкурсов для студентов, писал наставления учителям математики и курировал преподавание в училищах и гимназиях. Благодаря его действиям многие сотрудники и студенты университета были спасены во время эпидемии холеры 1830 года, были избавлены от уничтожения астрономические инструменты, книги и здание университета во время большого пожара в Казани в 1842-м.