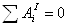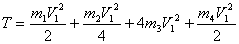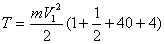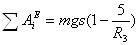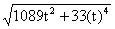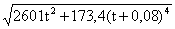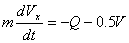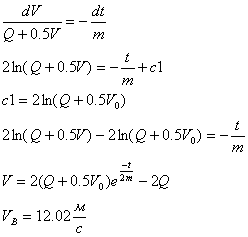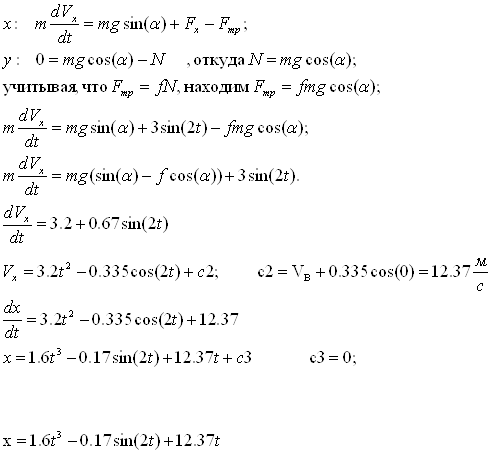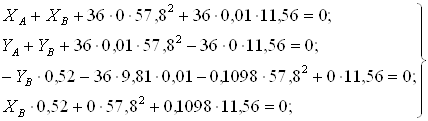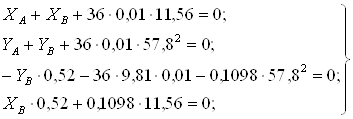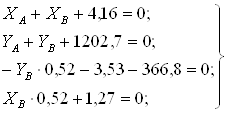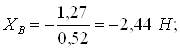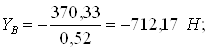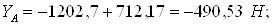в чем состоит задача механики
Учебники
Журнал «Квант»
Общие
Кикоин А.К. Как решается основная задача механики? //Квант. — 1984. — № 2. — С. 24-25.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Основная задача механики, как неоднократно указывается в учебнике «Физика 8», — определять положение (координаты) движущегося тела в любой момент времени. Это механика обязательно должна «уметь», иначе она не может быть наукой о движении. Законы движения, открытые Ньютоном, и прежде всего второй закон Ньютона (основной закон динамики) \(
\vec F = m \vec a\) как раз и позволяют решать эту задачу.
Второй закон Ньютона связывает силу, приложенную к телу, и вызванное силой ускорение. Но ускорение — это быстрота изменения скорости, а скорость, в свою очередь, — быстрота изменения перемещения тела. Поэтому, решив уравнение, выражающее основной закон динамики, мы узнаем о быстроте изменения координат тела, а значит, и о самих координатах в любой момент времени. Для этого кроме силы нужно знать еще начальные условия — начальные координаты и начальную скорость тела.
На первый взгляд кажется, что уравнение второго закона Ньютона очень простое и что решается оно тоже просто. Однако надо помнить, что уравнение \(
\vec F = m \vec a\) — векторное. Это значит, что за ним «скрываются» три скалярных уравнения для проекции силы и ускорения на оси координат:
Эти уравнения в самом деле решаются легко, но только в том случае, когда проекции силы Fx, Fy и Fz постоянны, то есть когда их значения одинаковы при любых значениях координат точки, а значит, и в любой момент времени. Тогда постоянны и значения проекций ускорения ax, ay и az, движение тела, следовательно, равноускоренное, и координаты х, у и z определяются равенствами
Здесь x0, y0 и z0 — начальные координаты, a υ0x, υ0y и υ0z — соответствующие проекции начальной скорости на оси координат.
В школьном курсе физики рассматриваются только такие задачи, когда силы постоянны. Значительно сложнее решать основную задачу механики, если сила и ее проекции зависят от координат. В действительности обычно именно так и бывает. Как решается задача в таком случае? Конечно, и теперь нужно знать начальные условия и силу. Но теперь «знать силу» — значит знать, как она изменяется при изменении координат тела.
Пусть, например, на тело действует сила Fx, которая определенным (и известным) образом зависит от координаты х. Для определения координаты х тела в любой момент времени прежние формулы непригодны, потому что если сила Fx изменяется от точки к точке, будет изменяться и ускорение ax тела. Будем решать задачу постепенно, так сказать, шаг за шагом.
Сначала рассмотрим движение нашего тела в течение малого промежутка времени Δt, начиная с момента, который мы условимся считать начальным. В этот момент (t = 0) координата х тела, равна x0 (начальная координата), а скорость равна υ0x (начальная скорость). Промежуток Δt выберем настолько малым, чтобы в течение этого времени силу Fx, а значит, и ускорение ax можно было считать постоянными. Силу F0x мы знаем, поскольку нам известно, как сила зависит от координаты; a0x мы тоже знаем, так как \(
a_ <0x>= \frac
Затем рассмотрим движение тела в следующий столь же малый промежуток времени Δt. Начальной координатой теперь будет найденное нами значение x1 и начальной скоростью — значение υ1x. В течение этого второго промежутка на тело будет действовать уже другая сила — F1x. Ее значение мы найдем, зная зависимость силы от координаты. Соответственно другим будет и ускорение тела a1x. Таким образом, к концу второго промежутка времени скорость тела будет равна
Эти значения скорости и координаты будут начальными для движения тела в течение следующего, третьего, промежутка, и мы таким же способом найдем значения скорости и координаты к концу этого промежутка.. Так, «двигаясь» шаг за шагом, мы сможем определить координату х тела в любой момент времени. Аналогично можно найти и координаты y и z.
В рассмотренной нами процедуре нетрудно заметить систематическую ошибку, которую мы допускаем. Состоит она в том, что сила и ускорение считаются постоянными в течение каждого малого промежутка времени Δt, а в конце промежутка они скачком изменяются. Между тем в действительности и сила, и ускорение всегда изменяются непрерывно. Уменьшить эту ошибку можно, уменьшив значение Δt. Ошибка практически вовсе исчезнет, если промежутки времени сделать бесконечно малыми. Но тогда число наших «шагов» станет бесконечно большим, и процедура из-за этого сделается невозможной.
Специально для таких случаев разработан особый математический аппарат, называемый дифференциальным и интегральным исчислением (Ньютон придумал его именно для этой цели). С его помощью и решается основная задача механики. Но принцип решения именно тот, который мы здесь рассмотрели. Именно таким способом рассчитывают сложные механические движения (например, спутников и ракет) современные ЭВМ.
В заключение отметим следующее. Когда мы говорим, что основная задача механики — находить координаты движущихся тел по известным силам и начальным условиям, то это вовсе не значит, что только этим и занимается механика. Бывает и так, что движение тела, то есть его положение в любой момент времени, известно из наблюдений. Тогда законы движения позволяют найти силу, действующую на тело. Эта задача, так называемая обратная задача механики, столь же важна, как и рассмотренная нами прямая задача, но, как нетрудно понять, она значительно проще.
Механика
Механика является одним из разделов физики. Под механикой обычно понимают классическую механику. Механика – наука, изучающая движение тел и происходящие при этом взаимодействия между ними.
В частности, каждое тело в любой момент времени занимает определенное положение в пространстве относительно других тел. Если со временем тело меняет положение в пространстве, то говорят, что тело движется, совершает механическое движение.
Механическим движением называется изменение взаимного положения тел в пространстве с течением времени.
Основная задача механики – определение положения тела в любой момент времени. Для этого нужно уметь кратко и точно указать, как движется тело, как при том или ином движении изменяется его положение с течением времени. Другими словами – найти математическое описание движения, т. е. установить сязи между величинами, характеризующими механическое движение.
При изучении движения материальных тел используют такие понятия, как:
Классическая механика основана на принципе относительности Галилея и законах Ньютона. Поэтому, ее еще называют – механикой Ньютона.
Механика изучает движение материальных тел, взаимодействия между материальными телами, общие законы изменения положений тел со временем, а также причины вызывающие эти изменения.
Общие законы механики подразумевают, что они справедливы при изучении движения и взаимодействия любых материальных тел (кроме элементарных частиц) от микроскопических размеров до объектов астрономических.
Механика включает в себя следующие разделы:
Следует отметить, что это не все разделы, которые входят в механику, но это основные разделы, которые изучает школьная программа. Кроме разделов указанных выше существует еще ряд разделов как имеющих самостоятельное значение, так и тесно связанных между собой и с указанными разделами.
Появление дополнительных разделов связано как с выходом за границы применимости классической механики (квантовая механика), так и с детальным изучением явлений происходящих при взаимодействии тел (например, теория упругости, теория удара).
Но, несмотря на это, классическая механика не теряет своего значения. Она является достаточной для описания в широком диапазоне наблюдаемых явлений без необходимости обращаться к специальным теориям. С другой стороны она проста для понимания и создает базу для других теорий.
Механика имеет большое значение для многих разделов астрономии, особенно для небесной механики (где изучаются движения планет, звезд и т. д.).
Особое значение механика имеет для техники. В гидродинамике, аэродинамике, динамике машин и механизмов, теории движения наземных, воздушных и транспортных средст используют уравнения и методы теоретической механики.
Основная задача механики
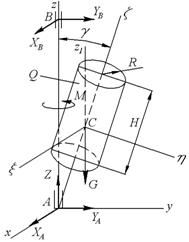
Механическая система под действием сил тяжести приходит в движение из состояния покоя, начальное положение системы показано на рис. 1. Учитывая сопротивление качению тела 3, катящегося без скольжения, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент времени, когда пройденный путь станет равным s.
В задании приняты следующие обозначения: m1, m2, m3, m4 – массы тел 1, 2, 3, 4; R3 – радиус большой окружности; δ – коэффициент трения качения.
Необходимые для решения данные приведены в таблице 1. Блоки и катки считать сплошными однородными цилиндрами. Наклонные участки нитей параллельны соответствующим наклонным плоскостям.
Применим теорему об изменении кинетической энергии системы:
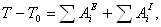
где T0 и T – кинетическая энергия системы в начальном и конечном положениях; 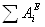
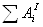
Для рассматриваемых систем, состоящих из абсолютно твердых тел, соединенных нерастяжимыми нитями,
Так как в начальном положении система находится в покое, то Т0=0.
Следовательно, уравнение (1) принимает вид:
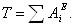
Кинетическая энергия рассматриваемой системы Т в конечном ее положении (рис.2) равна сумме кинетических энергий тел 1, 2, 3 и 4:
Кинетическая энергия груза 1, движущегося поступательно,
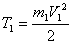
Кинетическая энергия барабана 2, совершающего вращательное движение,
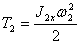
где J2x – момент инерции барабана 2 относительно центральной продольной оси:
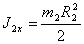
w2 – угловая скорость барабана 2:
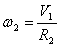
После подстановки (6) и (7) в (5) выражение кинетической энергии барабана 2 принимает вид:
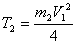
Кинетическая энергия колеса 3, совершающего плоскопараллельное движение:
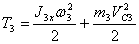
где VC3 – скорость центра тяжести С3 барабана 3, J3x – момент инерции барабана 3 относительно центральной продольной оси:
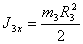
w3 – угловая скорость барабана 3.
Мгновенный центр скоростей находится в точке СV. Поэтому
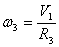
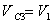
Подставляя (10), (11) и (12) в (9), получим:
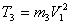
Кинетическая энергия груза 4, движущегося поступательно
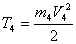
Кинетическая энергия всей механической системы определяется по формуле (3) с учетом (4), (8), (13), (15):
Подставляя и заданные значения масс в (3), имеем:
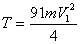
Найдем сумму работ всех внешних сил, приложенных к системе, на заданном ее перемещении (рис. 3).
Работа силы тяжести 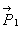
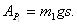
Работа силы тяжести 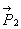
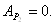
Работа пары сил сопротивления качению 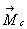
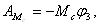
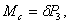
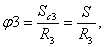
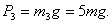
Подставляя (19), (20) и (21) в (18), получаем:
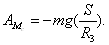
Работа силы тяжести 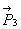
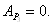
Работа силы тяжести 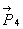

Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (17) – (24):
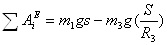
Подставляя заданные значения, получаем:
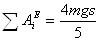
Согласно теореме (2) приравняем значения Т и 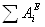
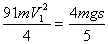
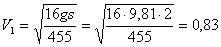
При t=0 x0=7 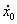
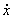
a=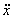
V=r2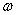
R2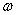
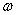
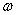
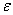
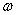
Vm=r3*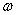
a t m=r3
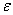
a t m=R3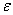
a n m=R3 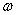
a=
При t=0 x0=6 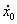
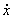
a=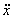
V=r2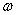
R2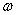
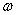
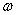
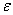
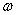
Vm=r3*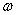
a t m=r3
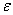
a t m=R3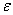
a n m=R3 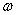
a=
Решение второй задачи механики
Определить: x = f(t) – закон движения груза на участке ВС
1) Рассмотрим движение на промежутке АВ
учитывая, что R=0.5V H;
Разделяем переменные и интегрируем
2) Рассмотрим движение на промежутке ВС (V0=VB)
Найти реакции в опорах А и В.
Для решения задачи используем систему уравнений, вытекающую из принципа Даламбера:

Для определения углового ускорения ε из последнего уравнения системы (1) найдем момент инерции тела относительно оси вращения z по формуле
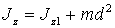
где Jz1− момент инерции тела относительно центральной оси Сz1, параллельной оси z; d – расстояние между осями z и z1.
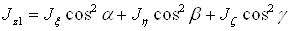
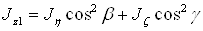
Определим моменты инерции тела 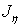
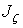
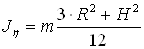
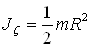
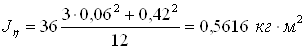
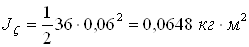
Определяем угол g из соотношения
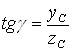
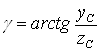
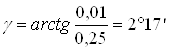
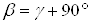
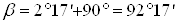
По формуле (4), вычисляем
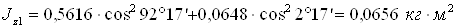
Момент инерции тела относительно оси вращения z вычисляем по формуле (2):
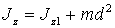
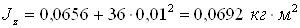
Из последнего уравнения системы (1)
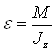
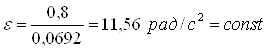
Угловая скорость при равноускоренном вращении тела
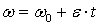
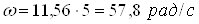
Для определения реакций опор следует определить центробежные моменты инерции 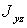
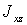
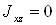
Центробежный момент инерции тела 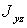
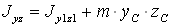
где 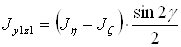
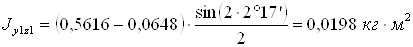
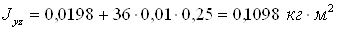
Подставляя известные величины в систему уравнений (1), получаем следующие равенства
Ответ: 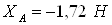
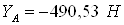
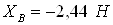
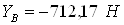
Определение скорости и ускорения точки по заданным уравнениям ее движения
Задание: по заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t1 (с) найти положение точки на траектории, ее скорость, касательное и нормальное ускорения, а также радиус кривизны траектории.
t1=1 (x и y – в см, t и t1 – в с).
Уравнения движения (1) можно рассматривать как параметрические уравнения траектории точки. Получим уравнения траектории в координатной форме.
x 2 + y 2 = (5cos(pt 2 /3)) 2 + (-5sin(pt 2 /3)) 2 ;
Получаем x 2 + y 2 = 25, т. е. траекторией точки является окружность, показанная на рис. 1.
Вектор скорости точки
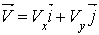
Вектор ускорения точки
Найдем их, дифференцируя по времени уравнения движения (1)

По найденным проекциям определяем модуль скорости:
и модуль ускорения точки:
а =
Модуль касательного ускорения точки
Модуль нормального ускорения точки
p – радиус кривизны траектории.
Модуль нормального ускорения точки можно найти и следующим образом:
После того как найдено нормальное ускорение по формуле (8), радиус кривизны траектории в рассматриваемой точке определяется из выражения:
Результаты вычислений по формулам (3)-(6), (8), (9) для момента времени t1=1с приведены ниже в таблице