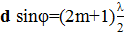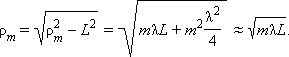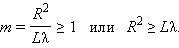в чем состоит явление дифракции

Дифракция

Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.

Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны и характерным размером неоднородностей среды , либо неоднородностей структуры самой волны. Наиболее заметно они проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, существенно превышающих длину волны (на 3—4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение волн с высокой степенью точности описывается законами геометрической оптики. С другой стороны, если размер неоднородностей среды много меньше длины волны, то в таком случае дифракции проявляет себя в виде эффекта рассеяния волн. [1]

Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным. Так, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн (в случае учёта их пространственного ограничения) в неоднородных средах.

Дифракция волн может проявляться:

Наиболее хорошо изучена дифракция электромагнитных (в частности, оптических) и акустических волн, а также гравитационно-капиллярных волн (волны на поверхности жидкости).

Содержание

Тонкости в толковании термина «дифракция»

В явлении дифракции важную роль играют исходные размеры области волнового поля и исходная структура волнового поля, которая подвержена существенной трансформации в случае, если элементы структуры волнового поля сравнимы с длиной волны или меньше её.

Например, ограниченный в пространстве волновой пучок имеет свойство «расходиться» («расплываться») в пространстве по мере распространения даже в однородной среде. Данное явление не описывается законами геометрической оптики и относится к дифракционным явлениям (дифракционная расходимость, дифракционное расплывание волнового пучка).

Исходное ограничение волнового поля в пространстве и его определённая структура могут возникнуть не только за счёт присутствия поглощающих или отражающих элементов, но и, например, при порождении (генерации, излучении) данного волнового поля.

Следует заметить, что в средах, в которых скорость волны плавно (по сравнению с длиной волны) меняется от точки к точке, распространение волнового пучка является криволинейным (см. градиентная оптика, градиентные волноводы, мираж). При этом волна также может огибать препятствие. Однако такое криволинейное распространение волны может быть описано с помощью уравнений геометрической оптики, и это явление не относится к дифракции.

Вместе с тем, во многих случаях дифракция может быть и не связана с огибанием препятствия (но всегда обусловлена его наличием). Такова, например, дифракция на непоглощающих (прозрачных), так называемых фазовых, структурах.

Поскольку, с одной стороны, явление дифракции света оказалось невозможным объяснить с точки зрения лучевой модели, то есть с точки зрения геометрической оптики, а с другой стороны, дифракция получила исчерпывающее объяснение в рамках волновой теории, то наблюдается тенденция понимать её проявление как любое отступление от законов геометрической оптики.

При этом следует заметить, что некоторые волновые явления не описываются законами геометрической оптики и, в то же время, не относятся к дифракции. К таким типично волновым явлениям относится, например, вращение плоскости поляризации световой волны в оптически активной среде, которое дифракцией не является.

Вместе с тем, единственным результатом так называемой коллинеарной дифракции с преобразованием оптических мод может быть именно поворот плоскости поляризации, в то время как дифрагированный волновой пучок сохраняет исходное направление распространения. Такой тип дифракции может быть реализован, например, как дифракция света на ультразвуке в двулучепреломляющих кристаллах, при которой волновые векторы оптической и акустической волн параллельны друг другу.

Ещё один пример: с точки зрения геометрической оптики невозможно объяснить явления, имеющие место в так называемых связанных волноводах, хотя эти явления также не относят к дифракции (волновые явления, связанные с «вытекающими» полями).

Раздел оптики «Оптика кристаллов», имеющей дело с оптической анизотропией среды, также имеет лишь косвенное отношение к проблеме дифракции. В то же самое время он нуждается в корректировке используемых представлений геометрической оптики. Это связано с различием в понятии луча (как направления распространения света) и распространения волнового фронта (то есть направления нормали к нему)

Отступление от прямолинейности распространения света наблюдается также в сильных полях тяготения. Экспериментально подтверждено, что свет, проходящий вблизи массивного объекта, например, вблизи звезды, отклоняется в её поле тяготения в сторону звезды. Таким образом, и в данном случае можно говорить об «огибании» световой волной препятствия. Однако, это явление также не относится к дифракции.

Частные случаи дифракции

Дифракция на щели

В качестве примера рассмотрим дифракционную картину возникающую при прохождении света через щель в непрозрачном экране. Мы найдём интенсивность света в зависимости от угла в этом случае. Для написания исходного уравнения используем принцип Гюйгенса.

Рассмотрим монохроматическую плоскую волну с амплитудой с длиной волны λ, падающую на экран с щелью ширины a.

Будем считать, что щель находится в плоскости x′-y′ с центром в начале координат. Тогда может предполагаться, что дифракция производит волну ψ, которая расходится радиально. Вдали от разреза можно записать

пусть (x′,y′,0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке (x,0,z). Щель имеет конечный размер в x направлении (от до ), и бесконечна в y направлении ([, ]).

Расстояние r от щели определяется как:

Предполагая случай дифракции Фраунгофера, получим условие . Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины). Используя биноминальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде:

Видно, что 1/r перед уравнением не осциллирует, то есть даёт малый вклад в интенсивность по сравнению с экспоненциальным множителем. И тогда его можно записать приближённо как z.

Здесь мы введём некую константу ‘C’, которой обозначим все постоянные множители в предыдущем уравнении. Она, в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля.

В случае дифракции Фраунгофера мало, поэтому . такое же приближение верно и для . Таким образом, считая , приводит к выражению:

Используя формулу Эйлера и её производную: и .

где ненормированная синкус функция определена как .

Подставляя в последнее выражение для амплитуды, можно получить ответ для интенсивности в виде волны в зависимости от угла θ:

Источник

Дифракция света

Дифракция света

Дифра́кция све́та — явление огибания светом преграды или прохождения через узкое отверстие. Это частный случай прямолинейности рапространения света. Наблюдается в среде с резкими неоднородностями. Свет отклоняется от прямолинейного распространения при прохождении его через малое отверстие или узкие щели (0,1—1,0 мм). В этом случае лучи света распространяются не только прямо, но и в стороны, отчего вокруг светлого кружка или светлой полосы появляется цветная кайма — дифракционные кольца или полосы. Первые легко наблюдать, если смотреть сквозь малое отверстие на стоящий недалеко источник света. Чем меньше отверстие, тем больше диаметр первого кольца дифракции. С увеличением отверстия его(первого кольца дифракции) диаметр уменьшается. Дифракция ухудшает резкость изображения при очень сильном диафрагмировании объектива. Она начинает сказываться с относительного отверстия 1:8—1:11

Вследствие дифракции при освещении непрозрачных экранов на границе тени, где, согласно законам геометрической оптики, должен был бы происходить скачкообразный переход от тени к свету, наблюдается ряд светлых и тёмных дифракционных полос.

Содержание

История изучения

Дифракционные явления были хорошо известны ещё во времена Ньютона, но объяснить их на основе господствовавшей в то время корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т. Юнгом. Независимо от него французский ученый О. Френель развил количественную теорию дифракционных явлений (1818 г.). В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Подтверждение теории Френеля на опыте явилось одним из основных доказательств волновой природы света. В настоящее время это теория носит название принцип Гюйгенса–Френеля и в ряде практически важных случаев решение дифракционных задач на основе этого принципа даёт достаточно хороший результат.

Литература

Яштолд-Говорко В. А. «Фотосъемка и обработка. Съемка, формулы, термины, рецепты.» Изд. 4-е, сокр. М., «Искусство», 1977.

Ссылки

См. также

Полезное

Смотреть что такое «Дифракция света» в других словарях:

ДИФРАКЦИЯ СВЕТА — в узком (наиболее употребительном) смысле явление огибания лучами света контура непрозрачных тел и, следовательно, проникновение света в область геом. тени; в широком смысле проявление волновых св в света в условиях, близких к условиям… … Физическая энциклопедия

дифракция света — дифракция Обусловленное волновой природой света явление отклонения от законов распространения света геометрической оптики, возникающее при прохождении света в среде с резкими оптическими неоднородностями. [Сборник рекомендуемых терминов. Выпуск… … Справочник технического переводчика

ДИФРАКЦИЯ СВЕТА — явления уклонения световых лучей, наблюдаемые, наприм., при прохождении их сквозь узкую щель в темную комнату. Если поставить в комнате на некотором расстоянии от отверстая белые ширмы, то на них получаются цветные полосы. Явление это объясняется … Словарь иностранных слов русского языка

Дифракция света — явления, наблюдающиеся при распространении света мимо резких краёв непрозрачных или прозрачных тел, сквозь узкие отверстия. При этом происходит нарушение прямолинейности распространения света, т. е. отклонение от законов геометрической… … Большая советская энциклопедия

дифракция света — šviesos difrakcija statusas T sritis fizika atitikmenys: angl. light diffraction vok. Lichtbeugung, f rus. дифракция света, f pranc. diffraction de la lumière, f … Fizikos terminų žodynas

Дифракция света — совокупность явлений которые обусловлены волновой природой света и наблюдаются при его распространении в среде с резко выраженными неоднородностями (напр. при прохождении через отверстия, вблизи границ непрозрачных тел и т. д.). В узком смысле… … Астрономический словарь

ДИФРАКЦИЯ СВЕТА НА УЛЬТРАЗВУКЕ — (акустооптическая дифракция). При распространении света в среде, в к рой присутствует УЗ волна, происходит дифракция света. Впервые Д. с. на у. была обнаружена П. Дебаем и Ф. Сирсом (США) и одновременно Р. Люка и П. Бикаром (Франция) в 1932.… … Физическая энциклопедия

дифракция света на ультразвуке — ultragarsinė šviesos difrakcija statusas T sritis fizika atitikmenys: angl. Debye Sears effect vok. Beugung des Lichtes an Ultraschallwellen, f; Debye Sears Effekt, m rus. дифракция света на ультразвуке, f; эффект Дебая Сирса, m pranc. effet… … Fizikos terminų žodynas

Дифракция — первого и второго порядка как интерференция волн, образованных при падении плоской волны на непрозрачный экран с парой щелей. Стрелками показаны линии, проходящие через линии интерференционных макси … Википедия

Дифракция электронов — Дифракция электронов процесс рассеяния электронов на совокупности частиц вещества, при котором электрон проявляет волновые свойства. Данное явление называется корпускулярно волновым дуализмом, в том смысле, что частица вещества(в данном… … Википедия

Источник

Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля

Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.

Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.

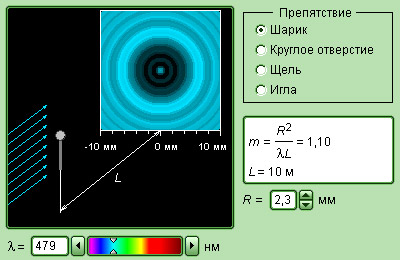
Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.

Принцип Гюйгенса-Френеля

Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в 1818 году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.

Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.

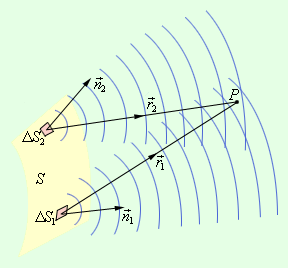
Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.

Предположим, что поверхность S – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновыми фронтами плоской волны считают семейством параллельных плоскостей, которые перпендикулярно направлены относительно распространения волны. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сферам.

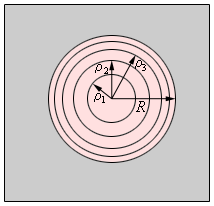
Для примера ниже приведена дифракционная задача прохождения плоской монохроматической волны, которая исходит от удаленного источника через отверстие с радиусом R непрозрачного экрана.

Чтобы расчеты были облегченными, волновая поверхность падающей волны разбивается на кольцевые зоны, называемыми зонами Френеля, исходя из правила: расстояния от границ соседних зон к точке Р имеют отличие на половину волны.

Зоны Френеля. Интерференционный максимум

Отличие от двух соседних точек расстоянием λ 2 говорит о том, что колебания, возбуждаемые этими зонами в состоянии противофазы. Соседние волны начинают гасить друг друга, а это приводит к тому, что суммарная амплитуда в точке запишется как:

Выражения в скобках равняются нулю, значит, амплитуда, вызванная волновым фронтом, равняется половине действий первой зоны.

Полученные пластинки обладают свойством фокусировки света, поэтому их называют зонными пластинками.

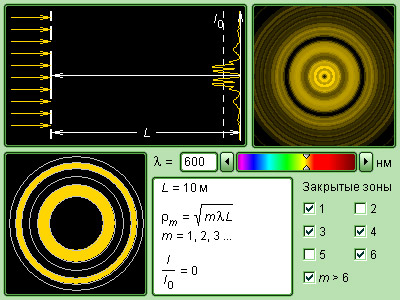
Круглый диск дает понять, что при дифракции зоны Френеля от 1 до m будут в закрытом состоянии. Отсюда получаем, что формула амплитуды колебаний примет вид:

Так как оптический диапазон имеет короткую волну, тогда соответственно зона Френеля также мала. Отчетливее проявление дифракционных явлений заметно при небольшом количестве зон на препятствии.

Получим формулы вида:

Когда количество зон Френеля из препятствия увеличивается, тогда дифракционные явления становятся незаметными:

Определение границы применимости геометрической оптики возможно при помощи заданного неравенства. При выполнении данного условия узкий пучок света может быть сформирован.

Отсюда следует вывод, что волновая оптика – это предельный случай геометрической.

При расчете видно, что радиусы ρ m зон Френеля на волне сферического фронта запишется, как

Выводы по теории Френеля справедливы.

Дифракция и интерференция света применима к любым волнам, так как имеется общность закономерностей. Начало XIX века – это было время, когда ученые только начинали изучать волны, а физическая природа света еще не была раскрыта.

Источник

ИССЛЕДОВАНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ СВЕТА

ЛАБОРАТОРНАЯ РАБОТА

Цель работы: ознакомление с дифракционными картинами различных типов; определение ширины прямоугольной щели при изучении явления дифракции в монохроматическом свете; определение длин волн красного и фиолетового света.

Приборы и принадлежности: дифракционная решетка, экран со щелью, линейка с делениями, осветитель, штатив; установка РМС – 3.

Явление дифракции состоит в отклонении света от прямолинейного распространения в среде с резкими неоднородностями в виде краев непрозрачных и прозрачных тел, узких отверстий, выступов и т.д., в результате чего свет проникает в область геометрической тени, и происходит интерференционное перераспределение интенсивности света. Под дифракцией следует понимать любое отклонение от прямолинейного распространения лучей, если только оно не является следствием обычных законов геометрической оптики – отражения и преломления. Явление дифракции объясняется волновыми свойствами света с использованием принципа Гюйгенса-Френеля.

Основные положения этого принципа:

1. Каждый элемент волновой поверхности, которой достигла в данный момент световая волна, служит источником вторичных волн, амплитуда которых пропорциональна площади элемента.

2. Вторичные волны, созданные элементами одной и той же по­верхности, когерентны и при наложении могут интерферировать.

3. Излучение максимально в направлении внешней нормали к элементу поверхности. Амплитуда сферической волны убывает с расстоянием от источника. Излучают только открытые участки волновой поверхности.

Этот принцип дает возможность утверждать отступления от пря­молинейного распространения в случае любой преграды. Рассмотрим случай падения плоской волны (параллельного пучка света) на преграду в виде отверстия MN в непрозрачной пластине (р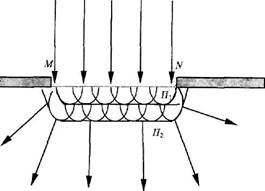ис.1).

Рис. 1

В соответствии с принципом Гюйгенса-Френеля каждую точку в плоскости отверстия MN можно рассматривать как самостоятельный источник света, испускающий элементарную сферическую волну. Поверхность П1, образованная элементарными волнами, определяет волновой фронт в момент времени t1. Эта поверхность П1 также становится источником вторичных элементарных сферических волн. Кривая, огибающая эти

элементарные волны в момент времени t₂, определяет волновой фронт с поверхностью П₂.

Из рис. 1 видно, что световые лучи, будучи перпендикулярны волновому фронту, отклоняются от своего первоначального направления и попадают в область геометрической тени.

Решить задачу о дифракции света – значит исследовать вопросы, относящиеся к интенсивности результирующей световой волны в различных направлениях. Основным вопросом при этом исследовании является изучение интерференции света, при которой налагающиеся волны могут не только усиливаться, но и ослабляться. Одним из важных случаев дифракции является дифракция в параллельных лучах. Она используется при рассмотрении действия оптических приборов (дифракционная решетка, оптические инструменты, и т. д.). Дифракционная решетка в простейшем случае представляет собой стеклянную прозрачную пластинку, на которой нанесены штрихи равной ширины на одинаковом расстоянии друг от друга. Такая решетка может быть использована в спектральной установке обычного типа вместо призмы как диспергирующая система. Чтобы легче было разобраться в довольно сложном физическом явлении интерференции дифрагированных пучков света на N щелях решетки, рассмотрим вначале дифракцию на одной, затем на двух щелях и, наконец, запишем выражение для N щелей. Чтобы упростить расчёт, используем метод зон Френеля.

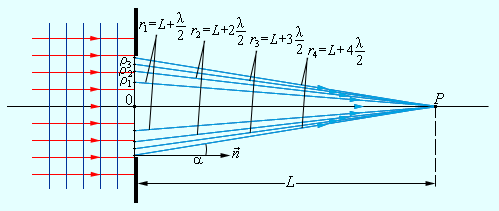
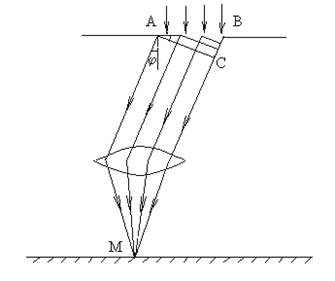
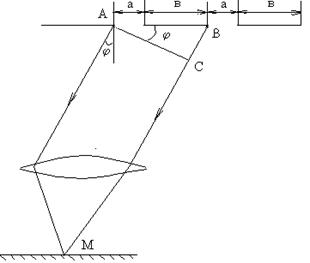
Дифракция на одной щели. Рассмотрим дифракцию в параллельных лучах на одной щели. Тип дифракции, при котором рассматривается дифракционная картина, образованная параллельными лучами, получил название дифракции в параллельных лучах, или дифракции Фраунгофера. Щель представляет собой прямоугольное отверстие в непрозрачной пластине, причем одна из сторон намного больше другой. Меньшая сторона называется шириной щели а. Такая щель является препятствием для световых волн, и на ней можно наблюдать дифракцию. В лабораторных условиях дифракция на щели отчетливо наблюдается, если ширина щели а сравнима по величине с длиной световой волны. Пусть монохроматическая световая волна падает нормально к плоскости щели шириной a (расстояние АВ). За щелью установлены собирающая линза и экран, помещённый в фокальной плоскости линзы. Схема представлена на рис. 2.

Согласно принципу Гюйгенса, каждая точка фронта волны, дошедшей до щели, является новым источником колебаний, причём фазы этих волн одинаковы, так как при нормальном падении света плоскость щели совпадает с плоскостью волнового фронта. Рассмотрим лучи монохроматического света от точек, лежащих на фронте АВ, направление распространения которых составляет угол 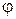с нормалью. Опустим из точки А перпендикуляр АС на направление луча, распространяющегося из точки В. Тогда, распространяясь дальше от АС, лучи не изменят разность хода. Разностью хода лучей является отрезок ВС. Для расчёта интерференции этих лучей применим метод зон Френеля.

Разделим отрезок ВС на отрезки длиной 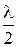. На ВС уложится z 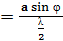таких трезков:

z , (1)

где .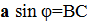

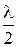
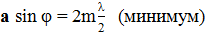
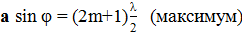
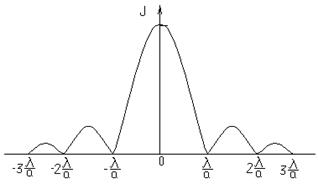
Проведя из концов этих отрезков линии, параллельные АС, до встречи с АВ, разобьем фронт волны в щели на ряд полосок одинаковой ширины, количество которых равно z. Они и являются зонами Френеля, так как соответствующие точки этих полосок являются источниками волн, дошедших до точки наблюдения М по данному направлению с взаимной разностью хода . Амплитуды волн от полосок будут одинаковы, потому что фронт плоский и площади их равны. Согласно теории зон Френеля, лучи от двух соседних зон гасят друг друга, так как фазы их противоположны. Тогда при чётном числе зон Френеля (z=2m, где m – целое число, m=1,2,3. ), укладывающихся в щели, в точке М будет минимум дифракции, а при нечётном (z=(2m+1)) – максимум. Уравнение (1) тогда запишем следующим образом:

,

.

Распределение интенсивности в дифракционной картине от одной щели показано на рис. 3. По оси абсцисс отложено расстояние от нулевого максимума вдоль экрана, на котором располагается спектральная картина.

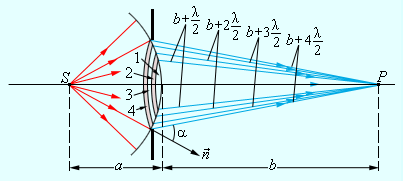
Дифракция на двух щелях. Для увеличения интенсивности и более чёткого разделения цветов пользуются не одной щелью, а дифракционной решёткой, которая представляет собой ряд параллельных щелей одинаковой ширины a, разделенных между собой непрозрачными промежутками шириной b. Сумма a+b=d называется периодом или постоянной дифракционной решетки.

Для того чтобы найти распределение освещенности на экране в случае решетки, необходимо учесть не только интерференцию волн, вышедших из каждой отдельной щели, но и взаимную интерференцию волн, пришедших в данную точку экрана из соседних щелей. Допустим, что имеется всего две щели. Монохроматическая волна падает нормально к плоскости щелей. Когда в щели укладывается четное число зон Френеля, выполняется условие минимума для щели. Поскольку для каждой щели выполняется условие минимума, то и для всей решетки тоже. Следовательно, условие минимума, для решетки совпадает с условием минимума для щели, оно называется условием главного минимума, и имеет вид

.

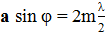
Рассмотрим случай, когда в щели укладывается нечетное число зон Френеля. При этом в каждой щели останется по одной нескомпенсированной зоне Френеля, в которой все источники света колеблются в одной фазе. Эти нескомпенсированные лучи, прошедшие через одну из щелей, будут интерферировать с нескомпенсированными лучами, прошедшими через другую щель. Выберем два произвольно направленных луча (рис. 4), исходящих из соответствующих точек соседних щелей и падающих в одну точку на экране. Их интерференцию определяет разность хода BC=dsin 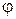. 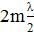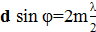Если BC= , то в точке М свет усилен. Уравнение

, (m=1,2,3…)

определяет главные максимумы. Если, 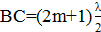, то в точке М свет ослаблен. Уравнение

является условием добавочных минимумов, появившихся вследствие наличия второй щели.

Если b>a, то ширина основной части дифракционной картины от двух щелей остаётся прежней. Большая часть энергии сосредоточена в пределах центрального максимума. Пунктиром показано распределение интенсивности для одной щели. Если b

Источник

В чем состоит явление дифракции

Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

Дифракционные явления были хорошо известны еще во времена Ньютона, но объяснить их на основе корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т. Юнгом. Независимо от него в 1818 г. французский ученый О. Френель развил количественную теорию дифракционных явлений. В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Принцип Гюйгенса в его первоначальном виде позволял находить только положения волновых фронтов в последующие моменты времени, т. е. определять направление распространения волны. По существу, это был принцип геометрической оптики. Гипотезу Гюйгенса об огибающей вторичных волн Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Принцип Гюйгенса–Френеля также представлял собой определенную гипотезу, но последующий опыт подтвердил ее справедливость. В ряде практически важных случаев решение дифракционных задач на основе этого принципа дает достаточно хороший результат. Рис. 3.8.1 иллюстрирует принцип Гюйгенса–Френеля.

Пусть поверхность представляет собой положение волнового фронта в некоторый момент. В теории волн под волновым фронтом понимают поверхность, во всех точках которой колебания происходят с одним и тем же значением фазы (синфазно). В частности, волновые фронта плоской волны – это семейство параллельных плоскостей, перпендикулярных направлению распространения волны. Волновые фронта сферической волны, испускаемой точечным источником – это семейство концентрических сфер.

Рассмотрим в качестве примера простую дифракционную задачу о прохождении плоской монохроматической волны от удаленного источника через небольшое круглое отверстие радиуса в непрозрачном экране (рис. 3.8.2).

Из рис. 3.8.2 легко найти радиусы зон Френеля:

Здесь – не обязательно целое число. Результат интерференции вторичных волн в точке зависит от числа открытых зон Френеля. Легко показать, что все зоны имеют одинаковую площадь:

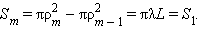С хорошим приближением можно считать, что амплитуда колебаний, вызываемых некоторой зоной, равна среднему арифметическому из амплитуд колебаний, вызываемых двумя соседними зонами, т. е.

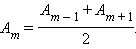Итак, если отверстие в непрозрачном экране оставляет открытой только одну зону Френеля, то амплитуда колебаний в точке наблюдения возрастает в 2 раза (а интенсивность – в 4 раза) по сравнению с действием невозмущенной волны. Если открыть две зоны, то амплитуда колебаний обращается в нуль. Если изготовить непрозрачный экран, который оставлял бы открытыми только несколько нечетных (или только несколько четных) зон, то амплитуда колебаний резко возрастет. Например, если открыты 1, 3 и 5 зоны, то

Оценим размеры зон Френеля. Пусть, например, дифракционная картина наблюдается на экране, расположенном на расстоянии от препятствия. Длина волны света (красный свет). Тогда радиус первой зоны Френеля есть

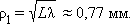Таким образом, в оптическом диапазоне вследствие малости длины волны размер зон Френеля оказывается достаточно малым. Дифракционные явления проявляются наиболее отчетливо, когда на препятствии укладывается лишь небольшое число зон:

Выше был рассмотрен случай дифракции света от удаленного источника на препятствиях круглой формы. Если точечный источник света находится на конечном расстоянии, то на препятствие падает сферически расходящаяся волна. В этом случае геометрия задачи несколько усложняется, так как теперь зоны Френеля нужно строить не на плоской, а на сферической поверхности (рис. 3.8.4).

Расчет приводит к следующему выражению для радиусов зон Френеля на сферическом фронте волны:

Все выводы изложенной выше теории Френеля остаются справедливыми и в этом случае.

Следует отметить, что теория дифракции (и интерференции) световых волн применима к волнам любой физической природы. В этом проявляется общность волновых закономерностей. Физическая природа света в начале XIX века, когда Т. Юнг, О. Френель и другие ученые развивали волновые представления, еще не была известна.

Источник